基于交互式多模型卡尔曼滤波的AUV超短基线跟踪算法

张晓飞, 辛明真,2, 隋海琛, 雷 鹏, 柳义成, 阳凡林,2*

基于交互式多模型卡尔曼滤波的AUV超短基线跟踪算法

张晓飞1, 辛明真1,2, 隋海琛3, 雷 鹏3, 柳义成3, 阳凡林1,2*

(1. 山东科技大学 测绘与空间信息学院, 山东 青岛, 266590; 2. 自然资源部海洋测绘重点实验室, 山东 青岛, 266590; 3. 交通运输部 天津水运工程科学研究所, 天津, 300456)

在复杂海洋环境下, 利用超短基线对自主水下航行器(AUV)进行跟踪定位可能会受到各类误差的影响, 通常采用以最小均方误差为准则的卡尔曼滤波对动态定位数据进行处理。构建起与目标实际运动相匹配的运动模型, 是保证卡尔曼滤波精度和可靠性的重要基础, 而AUV具有机动性较强的特点, 往往难以先验性地确定单一的运动模型实现对所有运动状态的匹配。针对基于单模型卡尔曼滤波无法全程适应水下目标的所有运动状态的问题, 采用交互式多模型卡尔曼滤波方法处理AUV的超短基线跟踪数据, 运动模型之间通过概率矩阵转移来增强运动状态的适应性, 实验结果表明该算法在多模型集合构建合理的情况下, 其状态适应性优于单模型卡尔曼滤波算法。

自主水下航行器; 超短基线; 交互式多模型; 卡尔曼滤波; 运动模型

0 引言

水下定位与导航是探索和开发海洋的基础。声波在水体中良好的传播特性使得水声定位与导航技术得到了广泛应用。水声定位系统主要包括长基线(long baseline, LBL)定位系统、短基线 (short baseline, SBL)定位系统、超短基线(ultra short baseline, USBL)定位系统和全球卫星导航声学浮标(global navigation satellite system-acoustic buoys, GNSS-AB)定位系统等[1-4], 其中LBL、SBL和GNSS-AB通过距离交会定位获取水下目标位置, 定位精度较高但系统操作繁琐[5]; USBL定位系统利用测距测向进行水下目标跟踪定位[6], 凭借其集成度高且操作性好的优势得到广泛应用[7]。

受海洋环境动态变化的影响, 采用USBL定位系统对自主水下航行器(autonomous undersea vehicle, AUV)进行跟踪定位可能受到各类误差的严重影响, 通常采用卡尔曼滤波(Kalman filter, KF)提高水下跟踪定位的精度和可靠性, 而构建起与目标实际运动状态相一致的运动模型是保证滤波稳定性的重要前提[8]。目前常用的运动模型主要包括匀速模型(constant velocity, CV)和匀加速模型(constant acceleration, CA)等非机动模型, 以及Singer模型[9]、“当前”统计(current statistical, CS)模型[10]和Jerk模型[11]等机动模型。然而, 相比于航空目标和陆上目标, AUV的运动速度相对较慢, 但机动性较强, 除了按照设计测线所进行的匀速或匀加速直线运动外, 还存在测线以外的机动运动状态, 如进入设计测线前的航迹调整、规避障碍物的随机运动等。因此在先验性地采用单一运动模型的情况下, 若AUV的运动状态发生变化, 就会导致基于单模型的KF方法的滤波精度下降, 最终可能导致滤波发散。

为了提高对机动目标运动状态变化的适应能力, Blom等[12]基于广义伪贝叶斯理论提出了交互式多模型(interacting multiple model, IMM) 算法, 随后IMM-KF在机动目标导航滤波中得到了广泛研究和应用。Hou等[13]提出了基于加权Kullback- Leibler散度的不确定目标跟踪交互式多模型滤波, 解决了模型相互关联或系统存在不确定性时发散的问题。Afshari等[14]利用IMM自适应估计方法, 实现了对机动目标的稳定控制。邹翔宇[15]提出基于IMM的迭代无偏转换测量KF算法, 解决了单模型的滤波方法无法对运动状态变化的目标跟踪等问题。张扬[16]利用机动检测法和概率钳制法改进了传统的基于隐马尔可夫模型(hidden Markov model, HMM)的自适应IMM算法, 解决了目标由于机动切换而导致跟踪精度降低的问题。赵振轶等[17]提出了IMM-无迹卡尔曼滤波(unscented Kalman filter, UKF)算法和IMM-扩展卡尔曼滤波(extended Kalman filter, EKF)算法对水下目标进行跟踪, 认为在测量误差较高的情况下, IMM- UKF算法具有更高的跟踪精度。吴新宏等[18]提出了基于IMM的EKF算法, 有效提高了对蛇形机动目标加速度的估计精度。张蕾[19]提出了IMM- CV/CA/坐标转弯(coordinated tum, CT)模型算法, 实现了对空中强机动目标的跟踪。

尽管IMM-KF算法在导航定位领域得到了广泛研究, 但在AUV跟踪定位方面的研究应用相对较少。文中面向USBL跟踪AUV的滤波问题, 针对单模型KF算法无法全程适应运动状态变化的问题, 分析采用IMM-KF提高水下目标跟踪定位自适应机动能力的可行性, 分别利用基于USBL的AUV导航滤波仿真实验和实测实验对IMM-KF定位精度进行定量、定性分析, 从而为AUV跟踪定位的相关研究和实际应用提供参考。

1 USBL定位原理与运动模型

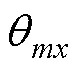
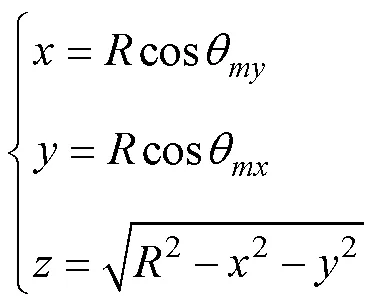
利用USBL定位系统对AUV进行跟踪定位可能会受到各类误差的影响, 通常采用KF对定位数据进行滤波处理, 其中运动模型对滤波精度有着直接影响。通常可将运动模型分为非机动模型和机动模型2类, 结合USBL的三维滤波对目前几种常用的运动模型介绍如下。

1) CV模型假设水下目标的运动状态为匀速直线运动, 其加速度为零。实际情况中, 环境因素会造成速度伴随着一定程度的随机噪声干扰, 通常采用连续时间的白噪声对其进行建模, 状态向量和状态转移矩阵为

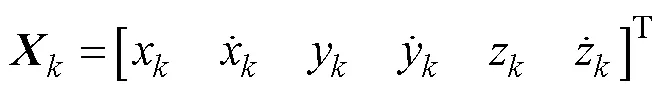
2) CA模型假设水下目标的运动状态为匀加速直线运动, 其加速度的时间变化率为零。加速度的随机扰动采用均值为零的高斯白噪声进行建模, 状态向量和状态转移矩阵为

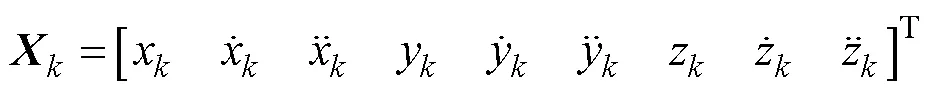
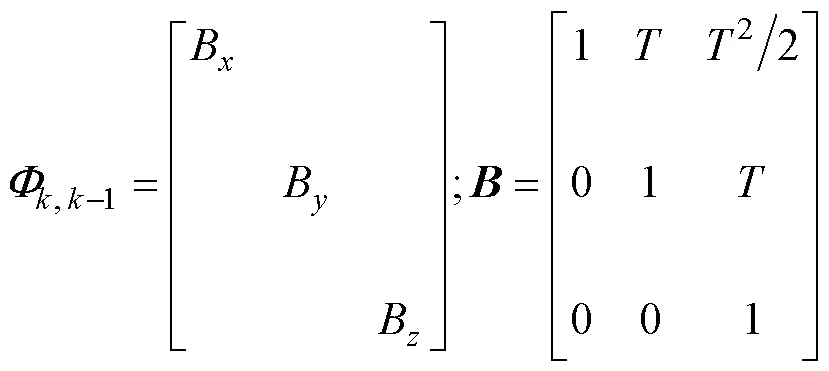
3) Singer模型将目标的加速度看作是一个零均值的指数自相关过程, 状态向量和状态转移矩阵为

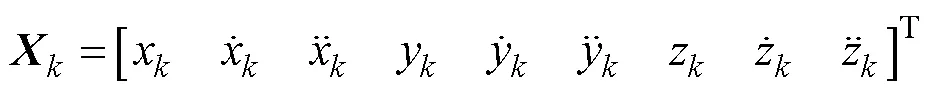
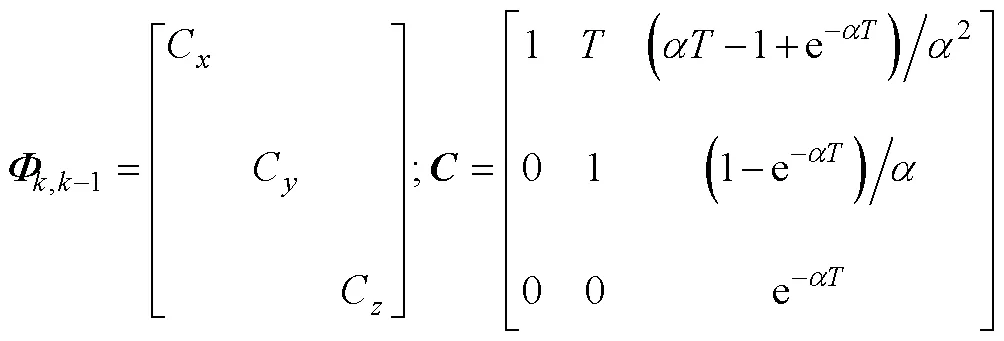
4) 当前统计模型是在Singer模型相关噪声建模的基础上, 将目标下一时刻加速度的取值约束在当前时刻加速度的邻域内, 目标加速度的当前统计概率密度服从修正瑞利分布, 状态向量、状态方程和控制矩阵表示为

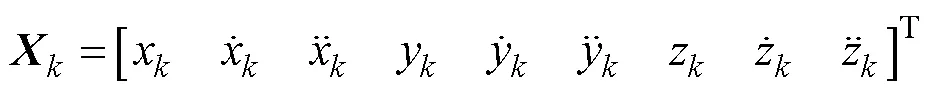
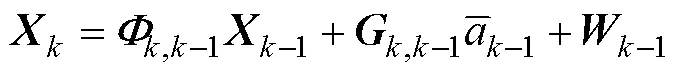
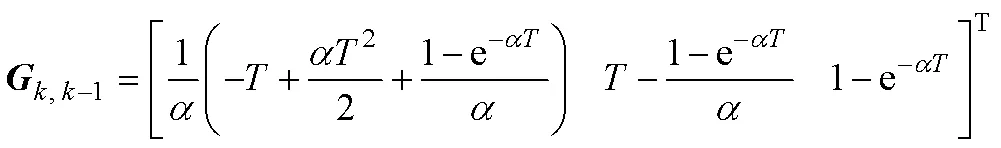
加速度方差可表示为

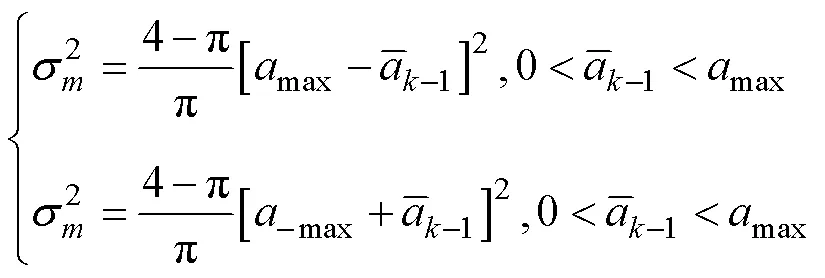
与Singer模型相比, CS模型利用前一时刻的加速度估值约束了下一时刻的加速度变化范围, 一定程度上具备了对加速度方差的自适应调整能力。

综上所述, 不同的运动模型适用于目标不同的运动状态, 尚不存在某种单运动模型能够满足所有的运动状态, 因此, 通过构建多模型集合实现交互式的KF方法成为解决这一问题的主要途径。

2 IMM-KF算法

由于采用单一的机动或者非机动跟踪模型无法全程适应目标的所有运动情况或者适应目标运动变化情况的效果较差, 发展出了一种具有马尔可夫概率转移矩阵的IMM-KF滤波算法, 其中多个运动模型同时进行工作, 算法中所有运动模型之间依靠概率矩阵进行转移, AUV的状态估计是多个卡尔曼滤波器共同作用的结果[12], IMM-KF算法原理如图2所示。

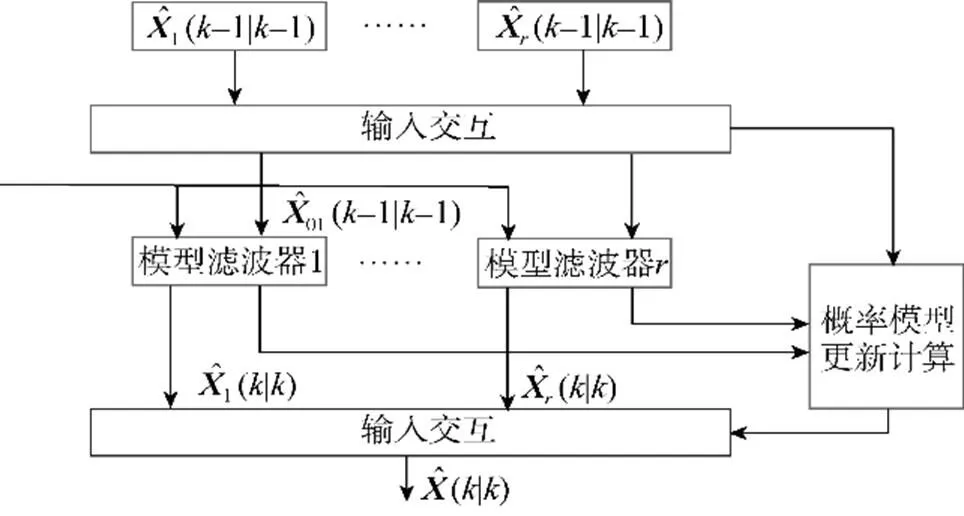
图2 IMM-KF算法原理图

假定AUV的运动过程中包含的运动状态有种, 假设第个模型的AUV状态方程为

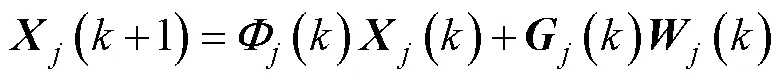
对应的量测方程为

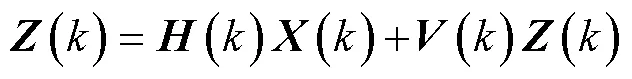
IMM-KF算法步骤如下。

1) 输入交互

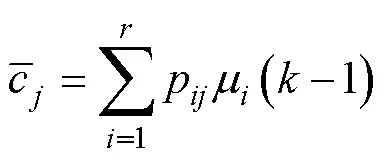
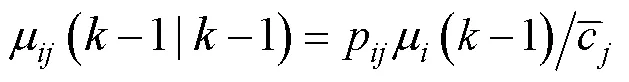
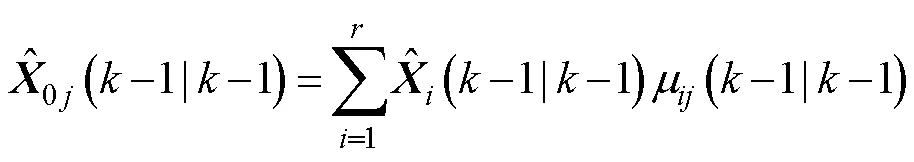
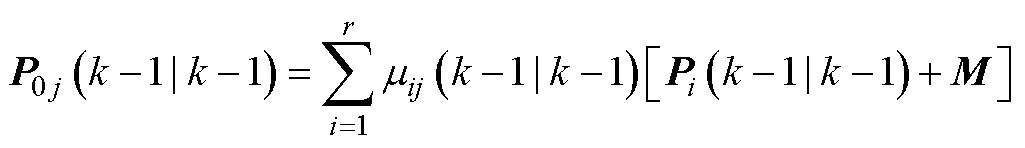
2) 卡尔曼滤波

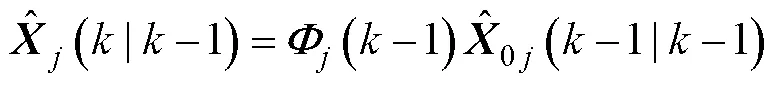
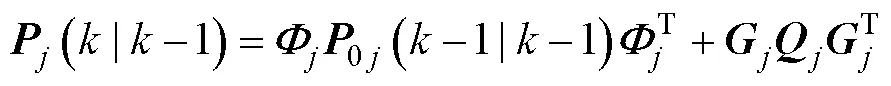
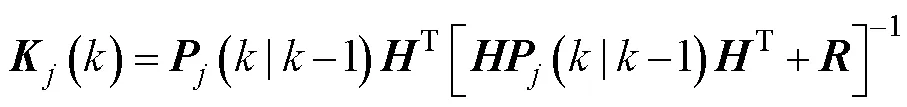
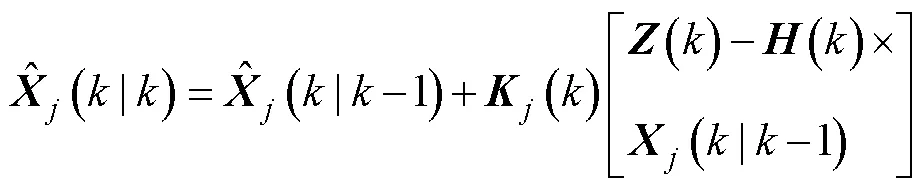
3) 模型概率更新

似然函数和概率为

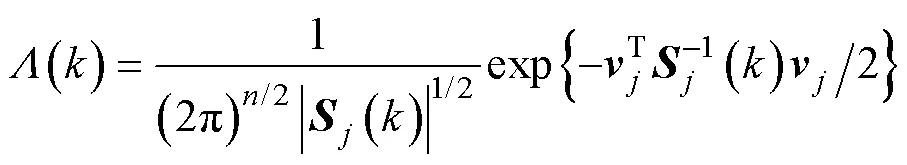
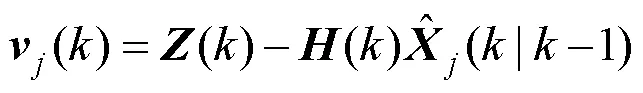
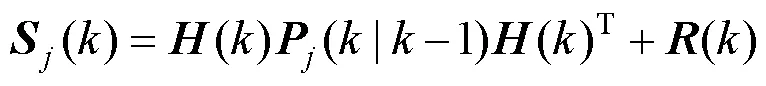
4) 输出交互

算法对每个模型的滤波结果进行加权融合, 然后得到了输出结果, 则AUV的状态融合估计和协方差融合估计为

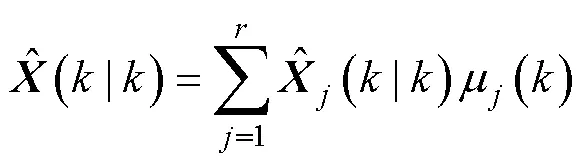
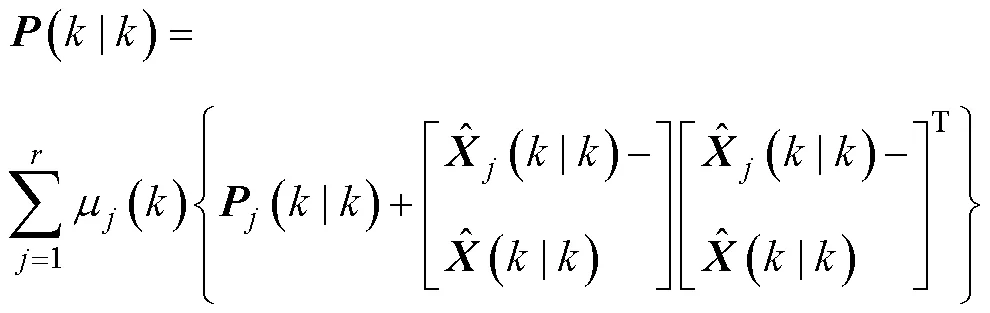
由IMM-KF算法的计算过程可以看出, 该算法利用多个运动模型构成的模型集合对AUV运动状态进行描述。当构建的运动模型集合与AUV的运动状态相匹配时, IMM-KF算法具有更好的跟踪效果; 但运动模型集合中包含过多的运动模型时, 会降低滤波效果。因此, 对于IMM-KF算法来说, 模型集合的构建尤为重要, 为此将结合AUV导航仿真实验和实测实验开展研究分析。

3 AUV导航仿真实验

设计了基于USBL的AUV导航滤波仿真实验, USBL定位误差为斜距的0.1%, 目标在1~300历元内, 在水平方向以0.5 m/s的速度作匀速直线运动; 在301~500历元内, 在水平方向作慢转弯运动; 在501~550历元内, 在水平方向作快转弯运动; 在551~900历元内, 在水平方向作变减速直线运动; 在1~900历元内, 目标在水深方向作匀减速运动。为了比较KF和基于不同运动模型集合的IMM-KF的导航滤波性能, 分别采用KF (CV)、KF(CA)、KF(Singer)、KF(CS)、IMM-KF(CV/ CA/Singer)、IMM-KF(CV/CA/CS)、IMM-KF (CV/ CS/Singer)和IMM-KF(CA/CS/Singer)进行处理。

KF导航滤波航迹如图3所示, KF导航滤波误差如图4所示, IMM-KF导航滤波航迹如图5所示, IMMKF导航滤波误差如图6所示, 导航滤波统计结果如表1所示。

对仿真结果分析如下。

1) 由单模型KF结果可以知道, 采用KF(CS)模型的滤波精度最高, 其点位中误差为1.706 m; 采用KF(CA)、KF(Singer)模型的滤波精度次之; 采用KF(CV)模型滤波精度最差, 其点位中误差为1.840 m。在目标的整个运动过程中, 水深方向作匀减速运动, 水平方向存在快速机动变化, 由于CS模型具备加速度方差的调整能力, 因此在所有单模型中滤波精度最高。

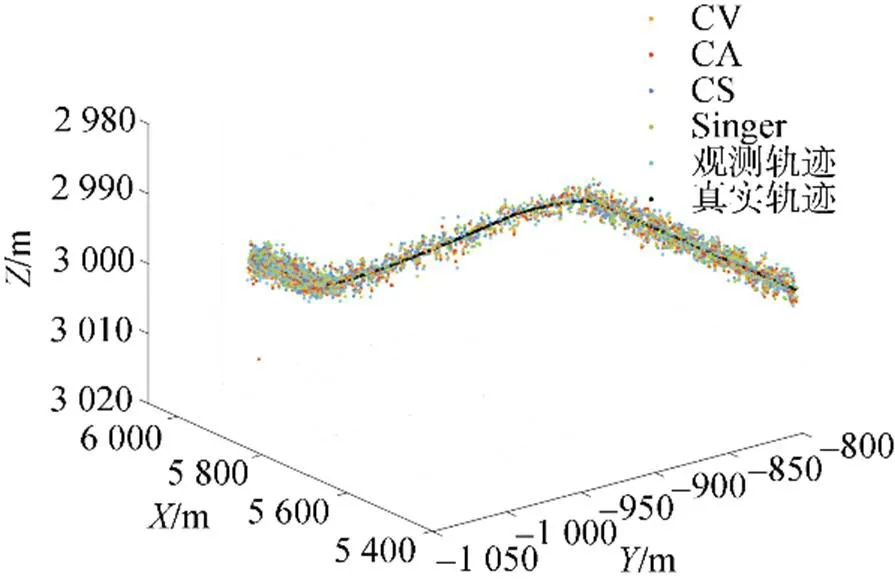
图3 单模型KF航迹仿真结果

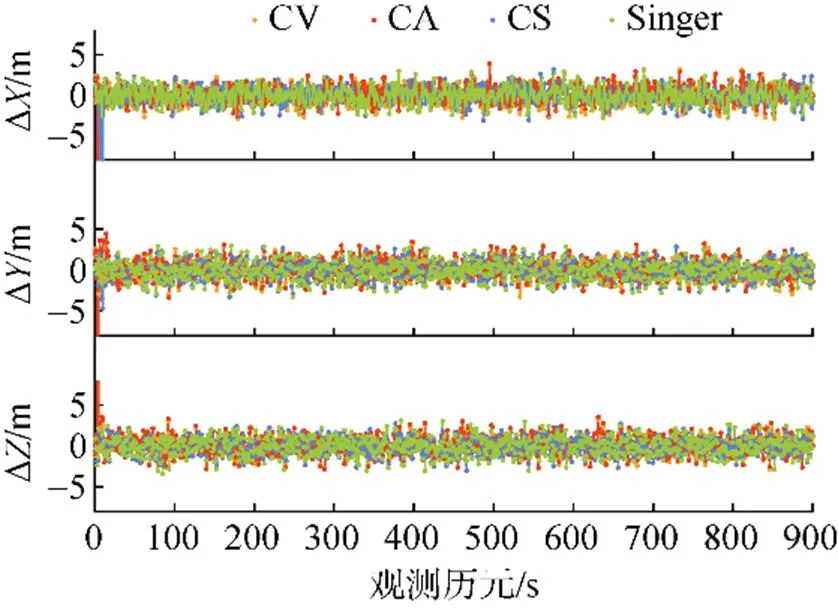
图4 单模型KF误差仿真结果

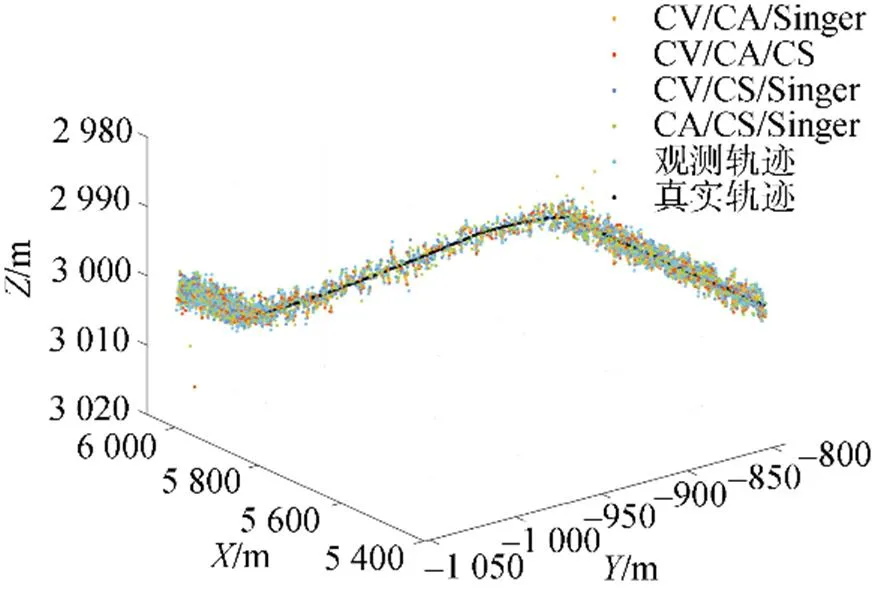
图5 IMM-KF航迹仿真结果

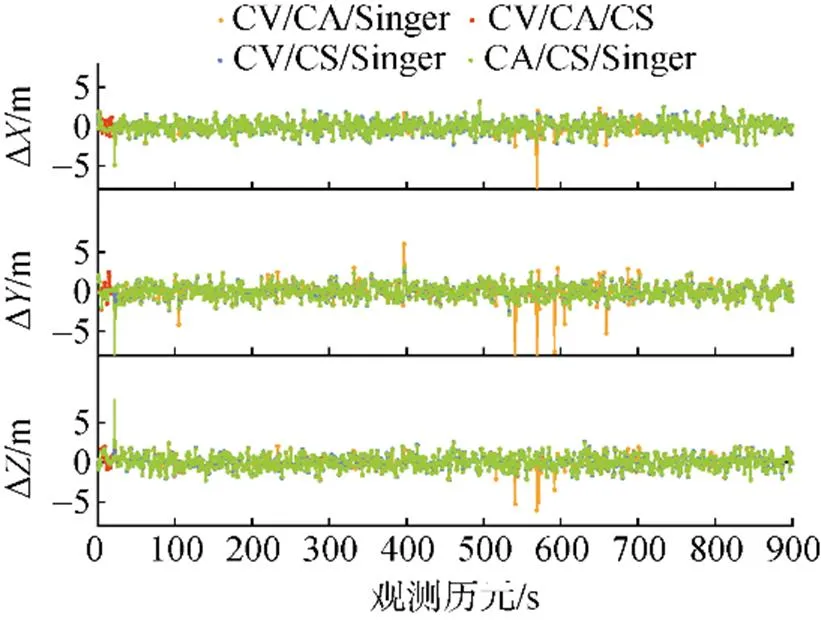
图6 IMM-KF误差仿真结果

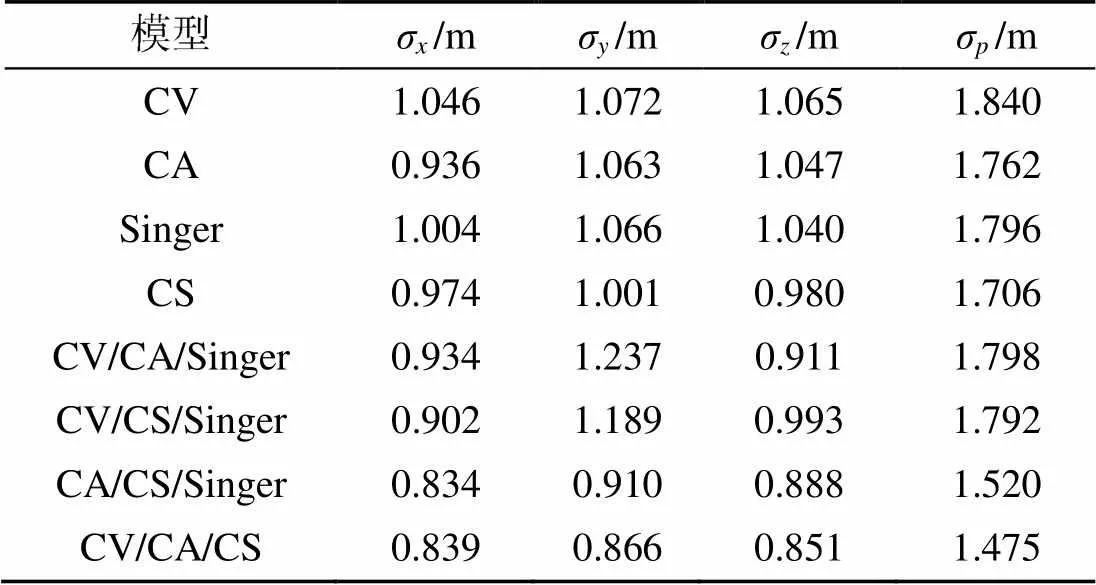
表1 基于USBL的AUV导航仿真实验统计结果

2) 由IMM-KF结果可知, 当采用IMM-KF (CV/CA/CS)和IMM-KF(CA/CS/Singer)模型时, 构建的运动模型集合与目标的实际运动相匹配, 保证了当目标的运动状态发生机动变化时, 可以利用IMM实现运动模型的自适应调整, 不仅避免了由于运动状态变化造成的滤波精度降低问题, 而且达到了较好的跟踪效果; 而IMM-KF(CV/CA/Singer)模型集合没有涵盖CS模型, 当目标的运动状态发生机动变化时, 不能自适应调整, 因此滤波精度差; 采用IMM-KF(CV/CS/Singer)模型时, 虽然涵盖了CS模型, 但是CV模型和Singer模型本身在机动状态的滤波精度有限, 因此其结果略优于IMM-KF (CV/CA/Singer)模型。

3) 对比KF和IMM-KF结果, 采用IMM-KF (CV/CA/CS)和IMM-KF(CA/CS/Singer)模型的滤波精度高于单模型KF的滤波精度; 而采用IMM- KF(CV/CA/Singer)模型的滤波精度比分别采用KF(CA)、KF(Singer)和KF(CS)模型的滤波精度差。因此, 在多模型集合构建合理的情况下, IMM-KF算法的状态适应性优于单模型KF算法, 否则不一定优于单模型KF。

4 AUV导航实测实验

实验中以AUV为跟踪对象, 实测数据中包含了USBL数据和深度计数据。为了比较KF和基于不同运动模型集合的IMM-KF导航滤波性能, 分别采用KF(CV)、KF(CA)、KF(Singer)、KF(CS)、IMM-KF(CV/CA/Singer)、IMM-KF(CV/CA/CS)、IMM-KF(CV/CS/Singer)和IMM-KF(CA/CS/Singer)进行处理, 将多传感器的组合导航(USBL/惯性导航系统/多普勒计程仪)跟踪结果作为参考值。KF导航滤波航迹如图7所示, KF导航滤波误差如图8所示, IMMKF导航滤波航迹如图9所示, IMMKF导航滤波误差如图10所示, 导航滤波统计结果如表2所示。

对实验结果分析如下。

1) 由单模型KF结果可知, 采用KF(CS)模型的滤波精度最高, 其点位中误差为1.907 m; 采用KF(CA)、KF(CV)模型的滤波精度次之; 采用KF (Singer)模型滤波精度最差, 其点位中误差为1.948 m。在目标的整个运动过程中, 水平方向的运动变化远大于深度方向, 整体上处于一种近似的变加速直线运动状态, 也存在非规律性的快速机动变化, 由于CS模型具备加速度方差的调整能力, 因此在所有单模型中滤波精度最高。也应注意到, 在CS模型的最大加速度固定取值的情况下, 深度方向较小的运动变化会使得滤波精度逐渐下降, 反映出CS模型对于弱机动目标跟踪性能较差的特点。

图7 单模型KF航迹实测结果

图8 单模型KF误差实测结果

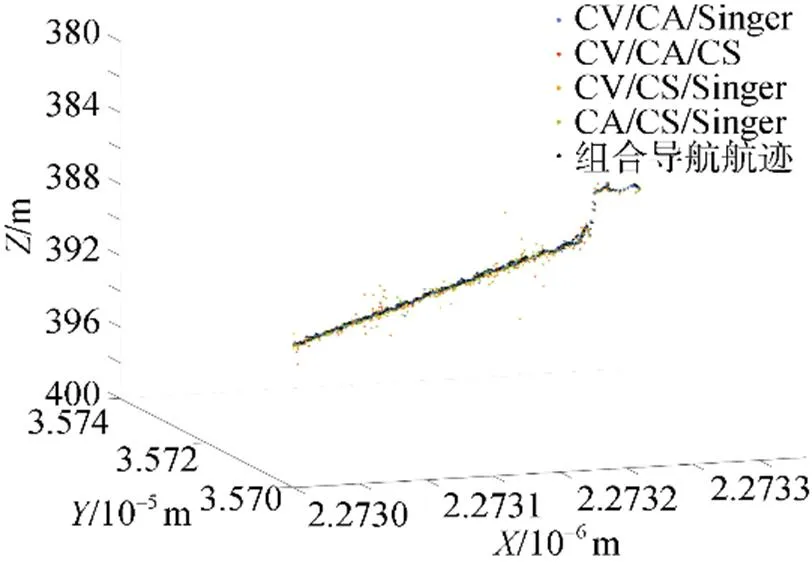
图9 IMM-KF航迹实测结果

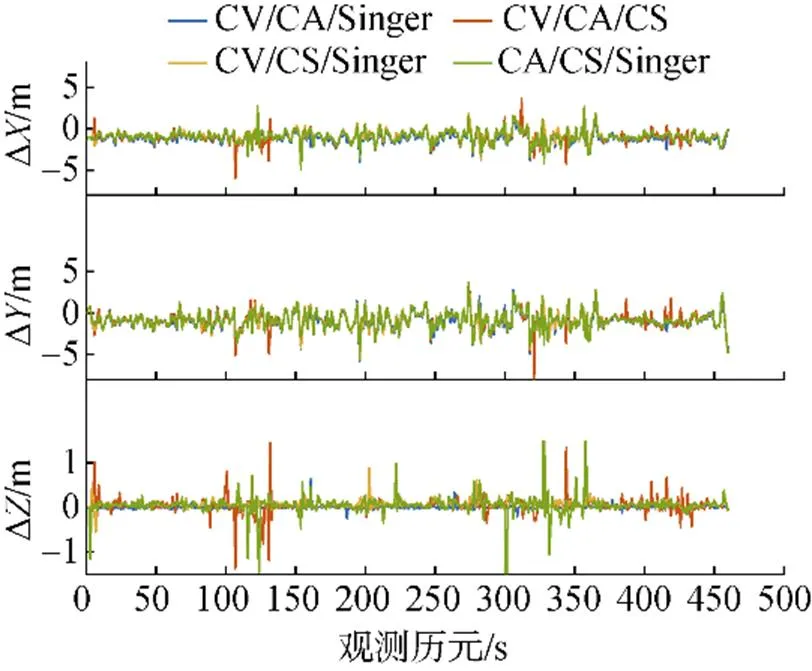
图10 IMM-KF误差实测结果

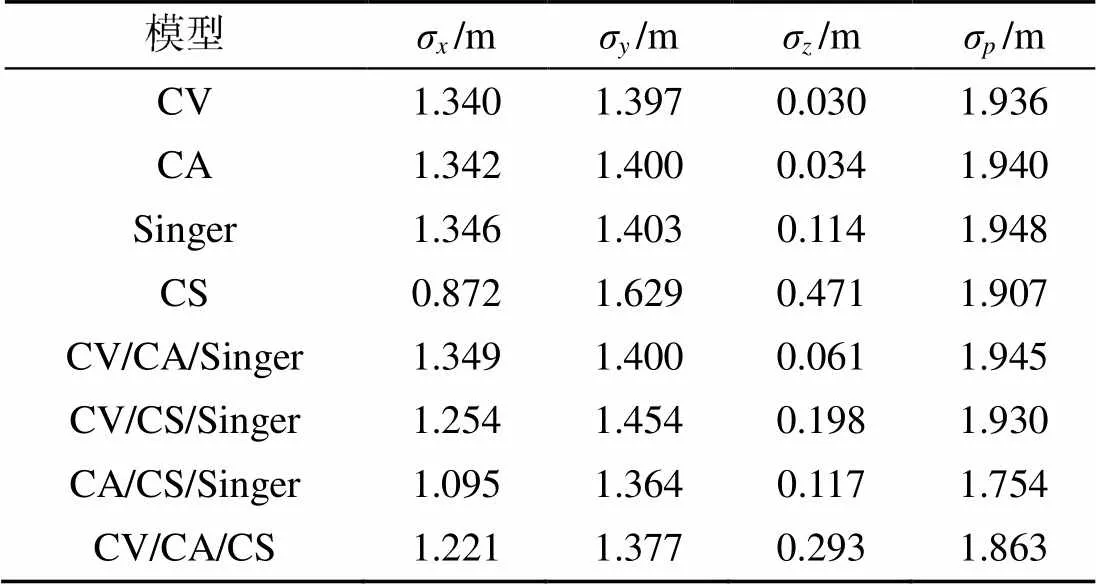
表2 基于USBL的AUV导航实测实验统计结果

2) 由IMM-KF结果可知, 当采用IMM-KF (CA/CS/Singer)模型时, 滤波精度最高, 其点位中误差为1.754 m, 当采用IMM-KF(CV/CA/CS)和IMM-KF(CV/CS/Singer)模型时, 滤波精度次之, 当采用IMM-KF(CV/CA/Singer)模型时, 滤波精度最差, 其点位中误差为1.945 m。当采用IMM- KF(CA/CS/Singer)和IMM-KF(CV/CA/CS)的模型时, 构建的运动模型与目标的实际运动状态相匹配, 保证了当目标的运动状态发生变化时, 可以利用IMM实现运动模型的自适应调整, 不仅避免了由于运动状态的变化造成的滤波精度降低问题, 而且达到了较好的跟踪效果; 当采用IMM-KF (CV/CA/Singer)模型时, 构建的运动模型集合没有涵盖CS模型, 当目标的运动状态发生机动变化时, 不能自适应调整, 导致滤波精度将降低; 采用IMM-KF(CV/CS/Singer)模型时, 虽然涵盖了CS模型, 但是CV模型和Singer模型本身在机动状态的滤波精度有限, 因此其结果仅仅略优于IMM-KF(CV/CA/Singer)模型。

3)对比KF和IMM-KF结果, 分别采用模型集合为IMM-KF(CA/CS/Singer)和IMM-KF(CV/ CA/CS)的滤波精度高于单模型KF的滤波精度; 而采用IMM-KF(CV/CS/Singer)和IMM-KF(CV/ CA/Singer)模型的滤波精度比单模型KF(CS)的滤波精度差。因此IMM-KF算法在多模型集合构建合理的情况下, 其状态适应性优于单模型KF算法, 否则不一定优于单模型KF。

5 结束语

在处理基于USBL的AUV跟踪定位问题时, 构建起与水下目标实际运动状态相一致的运动模型, 是保证KF精度和可靠性的重要前提。然而受复杂海洋环境动态变化的影响, AUV的运动状态具有低速度、高机动的特点, 难以先验性地确定水下目标的运动状态。因此, 当AUV运动状态发生变化时, 采用单一的机动或者非机动运动模型会使得滤波精度下降甚至滤波发散。文中分别采用仿真实验和实测实验对KF和IMM-KF进行测试分析, 结果表明单模型KF算法适应目标运动情况的效果较差, 当目标的实际运动状态与运动模型不一致时, 就会出现滤波精度降低的情况; 而IMM-KF算法在模型集合准确有效的情况下, 一定程度上克服了传统单模型KF算法无法全程适应目标运动状态变化的问题。

[1] Xin M Z, Yang F L, Liu H, et al. Single-Difference Dynamic Positioning Method for GNSS-Acoustic Intelligent Buoys Systems[J]. Journal of Navigation, 2020, 73(3): 646-657.

[2] Eric W, Michael A, John C, et al. Field Testing of Moving Short-baseline Navigation for Autonomous Underwater Vehicles Using Synchronized Acoustic Messaging[J]. Journal of Field Robotics, 2013, 30(4): 519-535.

[3] Huang J, Yan S G. A Precise Positioning Algorithm for Long Baseline Positioning System with Uncertain Sound Speed[C]//2nd International Conference on Applied Ma- thematics, Simulation and Modelling. Phuket, Thailand: Adv Sci & Ind Res Ctr, Phuket, 2017: 160-165.

[4] Francesco F, Niccolò M, Nicola P, et al. Development of an Ultra Short Baseline-aided Buoy for Underwater Targets Localization[J]. Journal of Engineering for the Maritime Environment, 2019, 233(4): 1212-1225.

[5] 辛明真, 阳凡林, 薛树强, 等. 顾及波束入射角的常梯度声线跟踪水下定位算法[J]. 测绘学报, 2020, 49(12): 1535-1542.

Xin Ming-zhen, Yang Fan-lin, Xue Shu-qiang, et al. A Constant Gradient Sound Ray Tracing Underwater Positioning Algorithm Considering Incident Beam Angle[J]. Acta Geo- daetica et Cartographica Sinica, 2020, 49(12): 1535-1542.

[6] 刘百峰, 罗坤. 超短基线定位系统误差分析与仿真[J]. 舰船电子工程, 2020, 40(5): 57-59, 84.

Liu Bai-feng, Luo Kun. Error Analysis and Emulator of Ultra-short Base Line System[J]. Ship Electronic Eng- ineering, 2020, 40(5): 57-59, 84.

[7] Liu H M, Wang Z J, Shan R, et al. Research into the Integrated Navigation of a Deep-sea towed Vehicle with USBL/DVL and Pressure Gauge[J]. Applied Acoustics, 2020, 159: 107052.

[8] 辛明真. GNSS-A水下定位与导航关键技术研究[D]. 青岛: 山东科技大学, 2020.

[9] 房晓丽, 陈玉敏, 方鑫钰. Singer模型算法在目标跟踪中的应用研究[J]. 电脑知识与技术, 2020, 16(27): 7-10.

Fang Xiao-li, Chen Yu-min, Fang Xin-yu. Research on Application of Singer Model Algorithm in Target Tracking[J]. Computer Knowledge and Technology, 2020, 16 (27): 7-10.

[10] 傅虹景, 于守江, 吉峰, 等. 基于“当前”统计模型的变结构交互多模型算法[J]. 无线电工程, 2020, 50(4): 318- 322.

Fu Hong-jing, Yu Shou-jiang, Ji Feng, et al. Variable Structure Interactive Multiple Model Algorithm Based on Current Statistical Model[J]. Radio Engineering, 2020, 50(4): 318-322.

[11] Meng Q H, Hou B W, Li D, et al. Performance Analysis and Comparison for High Maneuver Target Track Based on Different Jerk Models[J]. Journal of Control Science and Engineering, 2018, 2018: 1-6.

[12] Blom H A P, Bar-Shalom Y. The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients[J]. IEEE Transactions on Automatic Control, 1988, 33(8): 780-783.

[13] Hou B W, Wang J Q, He Z M, et al. Novel Interacting Multiple Model Filter for Uncertain Target Tracking Systems Based on Weighted Kullback-Leibler Divergence[J]. Journal of the Franklin Institute, 2020, 357(17): 13041-13084.

[14] Afshari H H, Dhafar Al-Ani, Saeid Habibi. A New Adaptive Control Scheme Based on the Interacting Multiple Model(IMM) Estimation[J]. Journal of Mechanical Scien- ce and Technology, 2016, 30(6): 2759-2767.

[15] 邹翔宇. 基于交互多模型的多滤波器机动目标跟踪研究[D]. 武汉: 武汉理工大学, 2019.

[16] 张杨. 改进的基于隐马尔可夫模型的自适应IMM算法[J]. 海军航空工程学院学报, 2018, 33(6): 531-538, 572.

Zhang Yang. Improved Adaptive IMM Algorithm Based on Hidden Markov Model[J]. Journal of Naval Aeronautical and Astronautical University, 2018, 33(6): 531-538, 572.

[17] 赵振轶, 李亚安, 陈晓, 等. 基于双观测站的水下机动目标被动跟踪[J]. 水下无人系统学报, 2018, 26(1): 40-45.

Zhao Zhen-yi, Li Ya-an, Chen Xiao, et al. Passive Tracking of Underwater Maneuvering Target Based on Double Observation Station[J]. Journal of Unmanned Undersea Systems, 2018, 26(1): 40-45.

[18] 吴新宏, 张紫琪, 王磊, 等. 基于自适应IMM算法的蛇形机动目标加速度估计研究[J]. 上海航天(中英文), 2020, 37(1): 18-23.

Wu Xin-hong, Zhang Zi-qi, Wang Lei, et al. Research on the Acceleration Estimation of Serpentine Maneuvering Target Based on the Adaptive IMM Algorithm[J]. Aerospace Shanghai(Chinese & English), 2020, 37(1): 18-23.

[19] 张蕾. IMM算法在雷达目标跟踪中的研究[J]. 民航学报, 2019, 3(1): 22-25, 4.

Zhang Lei. Research on IMM Algorithm in Radar Target Tracking[J]. Journal of Civil Aviation, 2019, 3(1): 22-25, 4.

[20] 金博楠, 徐晓苏, 张涛, 等. 超短基线定位技术及在海洋工程中的应用[J]. 导航定位与授时, 2018, 5(4): 8-20.

Jin Bo-nan, Xu Xiao-su, Zhang Tao, et al. USBL Technology and Its Applications in Ocean Engineering[J]. Na- vigation Positioning & Timing, 2018, 5(4): 8-20.

[21] 吴永亭, 周兴华, 杨龙. 水下声学定位系统及其应用[J]. 海洋测绘, 2003, 23(4): 18-21.

Wu Yong-ting, Zhou Xing-hua, Yang Long. Underwater Acoustic Positioning System and Its Application[J]. Hydr- ographic Surveying and Charting, 2003, 23(4): 18-21.

[22] 刘焱雄, 彭琳, 吴永亭, 等. 超短基线水声定位系统校准方法研究[J]. 武汉大学学报(信息科学版), 2006, 31 (7): 610-612.

Liu Yan-xiong, Peng Lin, Wu Yong-ting, et al. Calibration of Transducer and Transponder Positions[J]. Geomatics and Information Science of Wuhan University, 2006, 31 (7): 610-612.

[23] 冯守珍, 吴永亭, 唐秋华. 超短基线声学定位原理及其应用[J]. 海岸工程, 2002, 21(4): 13-18.

Feng Shou-zhen, Wu Yong-ting, Tang Qiu-hua. Principle and Application of Ultrashort Baseline Acoustic Positioning System[J]. Coastal Engineering, 2002, 21(4): 13-18.

AUV Ultra-short Baseline Tracking Algorithm Based on Interactive Multi-Model Kalman Filter

ZHANG Xiao-fei1, XIN Ming-zhen1,2, SUI Hai-chen3, LEI Peng3, LIU Yi-cheng3, YANG Fan-lin1,2*

(1. College of Geodesy and Geomatics, Shandong University of Science and Technology, Qingdao 266590, China; 2．Key Laboratory of Ocean Geomatics, Ministry of Natural Resources of China, Qingdao 266590, China; 3．Tianjin Research Institute for Water Transport Engineering, Ministry of Transport, Tianjin 300456, China)

Owing to complex marine environments, the tracking and positioning of autonomous undersea vehicles (AUVs) that use ultra-short baseline may be affected by various errors, and a Kalman filter based on the minimum mean square error is usually used to process the dynamic positioning data. It is important to ensure the accuracy and reliability of the Kalman filtering to construct a motion model that matches the actual motion of the target. However, the AUV is characterized by strong maneuverability, which often renders it difficult to a priori determine a single motion model to achieve the matching of all motion states. To address the inability of the single-model based Kalman filter to adapt to all the motion states of an underwater target, an interactive multi-model Kalman filter(IMMKF) algorithm was used to process the ultra-short baseline tracking data of an AUV. Furthermore, a probability matrix transfer between motion models was used to enhance the adaptability of motion states. The experimental results showed that the IMMKF algorithm was better than the Kalman filter algorithm for a single model when the multi model set was constructed reasonably.

autonomous undersea vehicle(AUV); ultra-short baseline; interactive multi-model; Kalman filter; motion model

张晓飞, 辛明真, 隋海琛, 等. 基于交互式多模型卡尔曼滤波的AUV超短基线跟踪算法[J]. 水下无人系统学报, 2022, 30(1): 29-36.

TJ630; P228

A

2096-3920(2022)01-0029-08

10.11993/j.issn.2096-3920.2022.01.004

2021-01-09;

2021-04-25.

国家重点研发计划(2018YFC0810400、2016YFB0501700); 国家自然科学基金(41930535); 山东省高等学校青创人才引育计划; 国家留学基金(202008370264); 中央级公益性科研院所基本科研业务费专项(TKS190302); 天津市交通运输科技发展项目(2018-b5).

通信作者简介:阳凡林(1974-), 教授, 博士生导师, 主要从事海洋测绘及全球卫星导航系统应用等研究.

(责任编辑: 杨力军)