涡轮叶片典型交叉肋结构的气热分析*
张俊峰 胡锡文 崔 凯 夏国正 陆禹铭 张 海
(1.中国核电工程有限公司;2.哈尔滨工程大学)
0 引言
随着燃气轮机在各种领域的广泛应用,对燃气轮机效率和推力的要求不断提高[1]。提高涡轮的进口温度可以达到提高燃气轮机热效率和推力的目的,研究表明:涡轮进口温度每提高55°,其功率和效率可提高10%[2]。所以提高涡轮进口温度是提升燃气轮机性能的重要途经[3]。但是提升后的燃气初温远高于涡轮叶片材料本身的耐高温极限,因此迫切需要发展叶片的冷却技术[4]。
目前世界上应用广泛的冷却方式主要有热障涂层冷却、气膜冷却[5]、对流冷却以及冲击冷却[6]。交叉肋冷却通道结构最早是在20世纪70年代由前苏联科学家发明并使用于燃气轮机高温涡轮叶片的冷却研究中[7],在强化换热方面有较好的效果。交叉肋冷却通道属于内部冷却方式,又被称为涡流矩阵通道(Matrix Cooling Channel)或网格肋通道[8]。Bunker[9]实验研究了交叉肋冷却结构在不同状态下的换热能力,实验结果显示交叉肋结构具有高换热性能,且壁面温度整体分布更加的均匀。Oh[10-11]等人对交叉肋冷却结构在旋转条件下进行换热和流阻特性实验,研究表明在静止条件下,吸力面和压力面子通道的努塞尔系数之比接近,随着旋转数增加,在吸力面上努塞尔系数之比增大,而压力面上变化不大。潘婷玉[12]对简化交叉肋模型进行数值模拟,计算结果表明肋片倾斜角在15°时综合换热效果最好。邓宏武等[13]对交叉肋结构和扰流柱结构进行实验研究,结果表明带交叉肋结构的通道换热效果好于带扰流柱结构的通道换热效果。
本文通过数值计算方法,研究了某型涡轮叶片内部交叉肋,通过改变几何参数进行气热分析,以期为燃气轮机涡轮叶片的交叉肋冷却方式提供思路。
1 数值计算方案
1.1 计算模型
现代燃机动叶前缘通常是热防护重点区域[14],图1所示为某型燃机涡轮叶片的交叉肋冷却结构,为了较好模拟涡轮叶片前缘内部,将图1(a)中所示红色虚线内区域简化为梯形截面内冷通道,模型设计按实际叶片尺寸进行模化,分别在通道进口和出口增加整流延长段,如图1(b)所示。模型设计厚度较小,代表叶片前部区域,气流从叶根垂直流入,经过交叉肋折转流出。保持整体尺寸不变,总长度为54mm。进口水力直径为8.06mm。同时本文设计了多组不同肋宽与肋间距之比w/t,肋倾角β的对比模型,不同几何参数如表1所示。
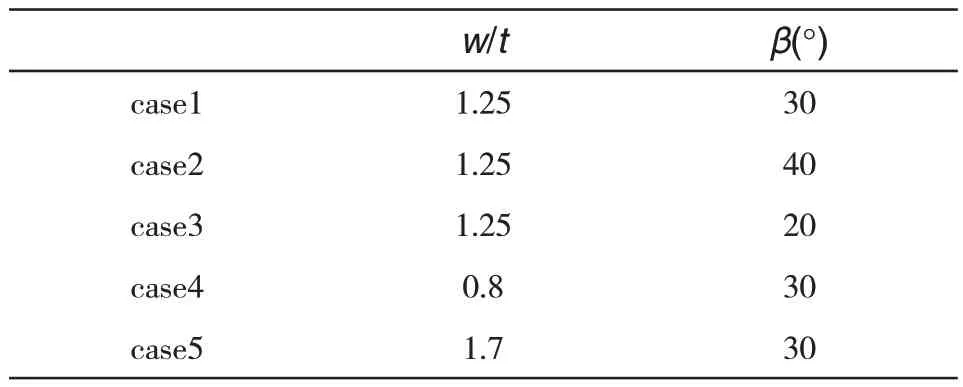
表1 交叉肋几何参数Tab.1 Geometric parameters of cross ribs

图1 某型涡轮叶片交叉肋Fig.1 A type of turbine blade cross rib
1.2 边界条件设置
边界条件为给定总温680K,进口雷诺数取6×104≤Re≤1×105,肋表面给定温度,其他壁面给定绝热无滑移壁面,出口给定静压1.04MPa。湍流模型利用SST湍流模型,收敛残差为10-6。同时,本文冷却气体在CFX里进行设置,采用的变比热容、变分子粘性以及热传导率。
1.3 网格划分和无关性验证
网格采用结构化网格划分,在肋近壁面处划分边界层,保证第一层网格高度为0.001mm,膨胀比为1.2,使其全局y+≈1。图2为前部交叉肋网格。

图2 前部交叉肋网格Fig.2 Front cross-rib grid
本文采用60万、120万、270万、400万和600万网格进行网格无关性验证,图3给出了不同数量网格计算的壁面平均努塞尔数随雷诺数的变化,可以发现网格数在240万以下时,模拟计算得到的数值偏小,当网格数达到270万以上时,可以看出曲线变化不大。因此本文选择了270万网格数量进行研究。

图3 不同数量网格计算的平均努塞尔数随雷诺数的变化Fig.3 The variation of the average Nusseltnumberwith Reynolds number for differentgrid number
1.4 评价指标
雷诺数是表征惯性力和粘性力的比值,本文雷诺数[15]计算表达式如下:
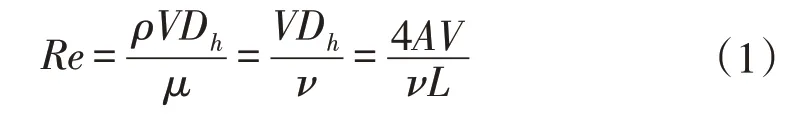
式中,ρ为进口气流密度;V为进口气流速度;Dh为水力直径;A为进口面积;L为进口湿周;μ为进口气流动力粘度,Pa·s;ν为运动粘度,m2/s。
换热特性采用努塞尔数(Nu)[16],它是跨越边界的对流热量与传导热量的比值,其表达式如下:

式中,h为换热系数;λ为热导率。
迪图斯-贝尔特(Dittus-Boelter)公式用于计算通过一个静止管道完全发展湍流的努塞尔数值(Nu0),因此换热增强比(Nu/Nu0)表达式如下所示:
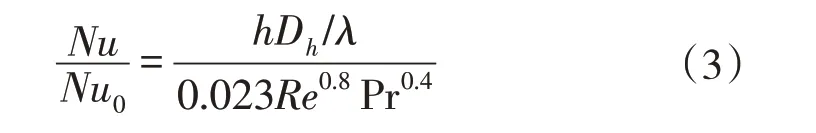
交叉肋通道流阻系数f采用以下公式计算:

由Blasius方程计算出光滑通道的摩擦系数f0:

定义流阻系数比为f/f0。引入综合热性能因子TPF(Thermal Performance Factor)来表示对流换热能力和压力损失的相对关系,其定义如下[17]:

2 肋倾角对流动换热的影响
本节主要研究不同肋角度前部交叉肋流动换热效果,图4给出了前部交叉肋壁面平均努塞尔数比、流阻系数比和综合换热效率。从图4(a)中可以看到20°时的Nu/Nu0最大,且随雷诺数增大先下降再增大再下降;当肋倾角为20°和30°时,随雷诺数增大而逐渐下降。从图4(b)可以看出在三个肋倾角的情况下f/f0都随着雷诺数增大而增大,其中肋倾角为20°时的阻力系数是最小的。图4(c)中20°肋倾角的综合换热效率最好,且各种肋倾角角度的交叉肋的综合换热效率都随着雷诺数的增加而下降。
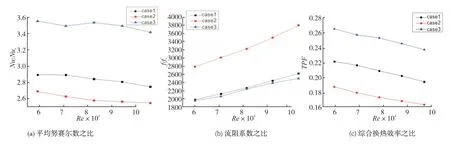
图4 不同肋倾角的交叉肋综合特性Fig.4 Comprehensive characteristics of cross ribs with different rib inclination angles
图5给出了不同角度肋倾角前部交叉肋的努塞尔数之比的分布图,左侧为进口,下方为出口。左侧进口附近可以看到努塞尔数之比非常大,该区域的换热能力非常好,可以带走大量热量,沿着叶片展向方向的努塞尔数之比逐渐变小,换热能力逐渐减弱,右上角处的努塞尔数之比是最小的,此处的流速也是最小,几乎没有对流换热的能力。右侧下方角区有强换热区域,结合图5(a)可以知道由于延长段局部回流增强局部湍流度和对流换热,同时图中也可以看到出口区域的努塞尔数之比要大于靠近叶片前缘区域的努塞尔数之比,这表明出口处的流动更为剧烈。case1和case3的努塞尔数之比明显大于case2,表明肋倾角角度较小时,有利于冷气在交叉肋通道中流动,冷气流动顺畅有利于增强换热。case2的肋倾角角度是40°,该结构只在进口处表现出高换热能力,而在展向方向的换热能力较弱,整体换热能力最不均匀,换热能力较差。

图5 不同肋倾角的交叉肋壁面努塞尔数之比分布图(Re=60000)Fig.5 Distribution of nus seltn umber ratio of cross ribs with different rib inclination ang les(Re=60000)
3 肋间距与肋宽之比对流动换热的影响
本节主要对不同肋宽与肋间距之比(0.8≤w/t≤1.7)的交叉肋的流动换热效果进行分析,图6是根据case1、case4、case5给出的前部交叉肋不同肋宽与肋间距之比的肋表面平均努塞尔数之比,流阻系数比和综合换热效率。可以看到不同肋宽与肋间距之比前部交叉肋Nu/Nu0和TPF值的变化趋势基本一致,都随着雷诺数的增加而趋向下降,但Nu/Nu0方面,case5>case4>case1,而TPF方面,case5>case1>case4。在流阻系数比方面,case4>case1>case5,case5的流阻系数比最小,因为肋宽固定,通道长度固定,因此肋间距增大一定会增大流道体积,由此可知通道的冷气量会增大,流阻就会减小。
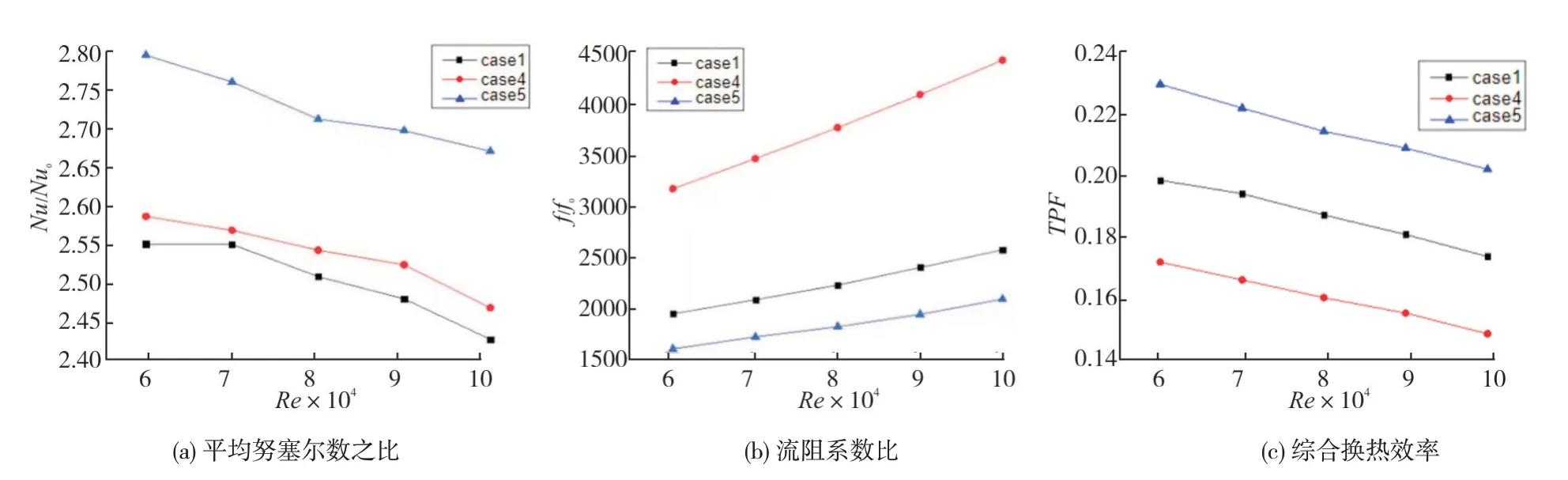
图6 不同肋宽与肋间距之比交叉肋综合特性Fig.6 Comprehensive characteristics of cross ribs with different ratios o f rib w idth to rib spacing
图7中给出了不同肋宽与肋间距之比的前部交叉肋Z=1.7mm和Z=-1.7mm截面马赫数分布图。图中可以看出进口处马赫数最高,靠近顶部马赫数最低,因此冷却流量也是最少。只有进口区域为高速区,其他区域基本都是低速区,换热能力较差。出口马赫数较高,压力较高,使得冷却气流在顶部和底部出口的空腔内具有较大涡系,这可以带走周围热量,增强换热能力。

图7 不同肋宽与肋间距之比前部交叉肋马赫数分布图(Re=60000)Fig.7 Distribution of Mach number of front cross ribs with different ratios of rib w id th to rib spacing(Re=60000)
图8中努塞尔数之比分布也出现上述现象,进口附近努塞尔数之比显著高于右上侧区域,努塞尔数之比多在6以上。

图8 不同肋间距与肋宽之比前部交叉肋努塞尔数之比分布(Re=60000)Fig.8 The ratio distribution of the frontcrossrib Nusseltnumber of different rib spacing torib width ratio(Re=60000)
4 基于响应曲面方法的前部交叉肋优化设计
图9是前部交叉肋的响应曲面图,图中左侧是肋倾角坐标轴,右侧为肋间距与肋宽之比坐标轴,纵向为综合换热系数(TPF)坐标轴。图中可以看到随着肋倾角增大,综合换热系数逐渐增大,随着肋间距与肋宽之比增大,综合换热系数先下降再逐渐增大。图中五角星为优化后交叉肋结构位置,圆圈为原交叉肋结构位置。在图中的综合换热系数最大值的位置就是优化后交叉肋结构位置,该值在肋倾角为20°,肋间距与肋宽之比为1.7处。

图9 前部交叉肋TPF响应曲面图Fig.9 TPF response surface of the front cross rib
图10是前部原始交叉肋结构和优化后交叉肋结构,在不同雷诺数下的综合换热系数对比图。图中可以清晰的看出,在不同雷诺数条件下,优化后交叉肋结构的综合换热效果都更好。

图10 不同雷诺数下前部交叉肋原结构与优化结构TPF值Fig.10 TPF values of the original structure and the optimized structure of the frontcross rib under different Reynolds numbers
在响应曲面中预测前部交叉肋在试验范围内换热与气动的综合效果最好的方案如表2所示,模拟计算的结果与响应曲面预测的结果相差5.15%。

表2 优化结果Tab.2 Optimization results
表3是原前部交叉肋结构和优化后交叉肋结构的几何参数和TPF值,对比可以看到前部交叉肋的综合换热效率提高了11.02%。

表3 原前部交叉肋结构与优化后结构的几何参数及综合换热效率Tab.3 Geometric parameters and comprehensive heat transfer efficiency of the original front cross rib structure and the optimized structure
图11和图12分别是原结构与改变结构参数的努塞尔数分布图。两组图中压力侧的换热效果要优于吸力侧的换热效果,且叶根处的换热效果也要优于叶顶。结构的改变对吸力侧靠近前缘处的部分低换热区换热效果有所增强,同时结构的改变降低了该部分交叉肋出口处的换热能力,但是结构的改变使得吸力侧的换热能力更加均匀。结构的改变增大了压力侧的高换热区面积,但是叶顶附近的换热能力稍显降低。

图11 原结构努塞尔数分布图Fig.11 Distribution of nusselt number of the originalstructure

图12 优化结构努塞尔数分布图Fig.12 Nusselt number distribution of optimized structure
5 结论
1)随着雷诺数的增加,努塞尔数之比逐渐下降,阻力系数之比逐渐增大,综合换热效率逐渐下降。
2)对比不同参数的交叉肋数值模拟,发现在相同雷诺数条件下,肋倾角为不同角度时,努塞尔数之比20°>30°>40°;不同肋间距与肋宽之比时,努塞尔数之比1.7>1.25>0.8。
3)对比不同参数的交叉肋数值模拟,发现在相同雷诺数条件下,肋倾角为不同角度时,流阻系数之比40°>30°>20°;不同肋间距与肋宽之比时,流阻系数之比0.8>1.25>1.7。
4)对比不同参数的交叉肋数值模拟,发现在相同雷诺数条件下,肋倾角为不同角度时,综合换热效率20°>30°>40°;不同肋间距与肋宽之比时,综合换热效率1.7>1.25>0.8。
5)当肋倾角为20°,肋间距与肋宽之比为1.7时综合换热效率最高,此时比原结构肋倾角为25°,肋间距与肋宽之比为1.55时提高了11.02%。
致谢:感谢中国航发稳定支持项目的支持。

