尾流作用下风机振动的控制研究
李秋明
(中铁第四勘察设计院集团有限公司)
0 引言
随着风能技术的发展,风电机组的发电容量也迅速扩大。为获得更大的容量,需要增大扫风面积以捕获更大的风能。上游风电机组对原风场产生扰动,使尾流区风场平均风速降低,湍流强度增大[1-4]。而风机尺寸的增大使得尾流区扩大,尾流特性更加复杂。已有研究表明[5-10],对于大型风电机组,尾流效应作用不容忽视,尾流区湍流强度的增加使下游风电机组疲劳荷载增大,风速降低使得下游风电机组输出功率减小。目前,对于尾流效应的影响,普遍采用的方法为“等效设计湍流强度”[11,12],用单一的设计参量代表原有的尾流效应。然而,随着风电机组尺寸的增大,该方法也逐渐失去其适用性。并且,无论是湍流度还是平均流场,尾流中的流场都会发生巨大的变化。因此,需要开展尾流作用下下游风电机组振动控制的相关研究,以减小尾流对其造成的不利影响。目前,关于此问题的相关研究并不多见,这可能是由于风机尾流与传统的大气边界层(ABL)有很大的不同,不适用于传统湍流生成方法[13],对确定尾流中运行的风力机的疲劳载荷带来许多困难,而且现有的商业程序也难以自定义尾流风场数据[14]。因此,必须进一步地研究尾流效应对机组载荷的影响,并对其进行尾流区风机振动控制来减小尾流效应对下游风电机组疲劳载荷的影响。
本文基于现有的致动线(ALM)理论,实现风机尾流风场仿真,以获取实时尾流风场数据;利用广义坐标系理论,在广义自由度下,建立塔架-叶片耦合体系的运动方程,编制陆上风机结构风致响应分析程序(AOWT),以实现考虑旋转叶片与塔架耦合整机时变体系风致响应分析。分别采用商业程序GH Bladed软件和自编程序对其进行分析,通过对比其计算结果,以验证自编程序的准确性。最后修改原运动方程,利用调谐质量阻尼器(TMD)、旋转惯性双调谐质量阻尼器(RIDTMD)进行风机结构振动控制,分析两种不同阻尼器最优控制参数,以及最优控制效果。
1 尾流风场仿真
1.1 控制方程
大涡模拟(Large Eddy Simulation,LES)利用亚网格尺度模型模拟小尺度涡旋对大尺度涡旋的影响,以获得滤波后的大尺度涡旋运动,滤波后的连续方程和动量方程如下:
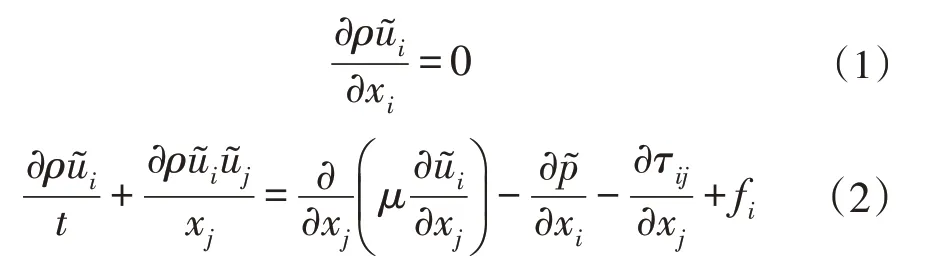
式中,和分别为滤波后的速度(u,v,w)与压强;μ为空气粘度;ρ为空气密度;τij为亚格子应力;fi为阻力源项,以表征风机对原流场的扰动效应。采用亚格子应力模型封闭以上方程[15]:
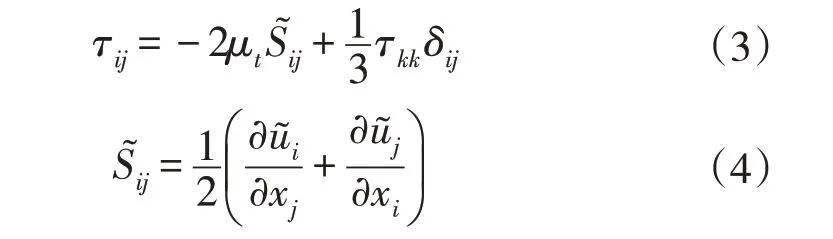
其中,μt为亚格子湍流黏性系数;为应变率张量。在求解μt时,本文采用Smagori-nsky-Lilly模型,其具体表达式为:
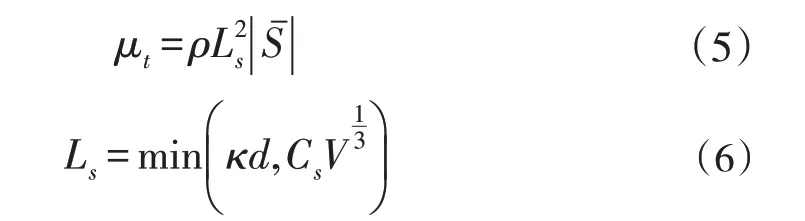
其中,Ls为亚格子混合长度;κ为冯卡门常数(0.42);d为到最近壁面的距离;Cs为Smagorinsky常数;V为控制体体积。在上述公式中,需要确定Smagorinsky系数Cs,在本文中,取Cs=0.032。
1.2 致动线(ALM)方法
为避免风机叶片贴体网格划分,在动量方程(式(2))中添加体积力源项(方程右第四项fi)以表征风机对原流场的扰动效应,详细计算过程如文献[16-17]所述。每个叶片都表示为一条随转子转速移动的线,并在计算气动力的径向截面上进行离散。
体积力源项可依据叶素动量理论(BEM)计算,将叶片沿径向离散为若干叶素,如图1所示,各叶素上的升力与阻力可按式(7)计算:

图1 叶素动量理论示意图Fig.1 Schematic diagram of BEM

式中,Cl与Cd分别表示升阻力系数,c为翼型弦长,Vrel为叶片与气流相对速度,可按图2中局部速度矢量三角形计算,即:

则,叶片所划过的网格单元添加的阻力源项为:
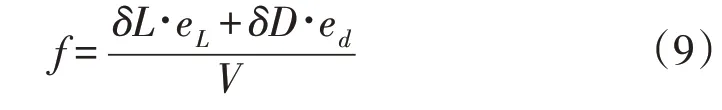
1.3 数值模型
本文采用缩尺比1:100的三菱MWt-1000模型风力发电机。缩尺模型的风轮直径D为0.57m,轮毂高度为0.7m。该风力机的额定风速Ur为10m/s。Ishihara等人[18]利用该模型机开展了风洞实验,获取了风机尾部流场信息。在该实验中,开展了两个不同的叶尖速度比(λ=5.52和9.69)和两个不同的流入紊流强度(Ia=0.035和0.137)下的四种工况。根据IEC规范第3版[19],考虑到该风力机在运行中的叶尖速比约为10.0,湍流强度始终在0.1到0.2之间,本文最后选择一个λ=9.69,Ia=0.137的工况进行研究。在该工况下,相应的俯仰角等于0°,推力系数CT=0.81。实验中轮毂中心处风速为10.2 m/s。雷诺数为ρUhHhub/μ,对于该缩尺度模型,等于4.8×105。风力发电机的关键参数见表1。关于本研究所选取风力发电机的详细参数,可参考Ishihara和Qian的相关研究[20]。

表1 MWt-100型号风机关键参数表Tab.1 Keyparam eters of wind turbines
为模拟传统的大气边界层条件,与Ishihara等人[18]开展的实验类似,在数值仿真中采用三个尖劈和一个围栏,人为制造湍流,如图2所示。计算域的长度、宽度和高度分别为15.5m、1.5m、1.8m。风力机位于进口下游8.0m处,轮毂中心为该计算域的原点(x=0,y=0,z=0)。三个尖劈布置在风机上游6.0m处,围栏位于风机上游5.5m处。在水平方向上,将风轮转子盘以0.01m的矩形网格单元均匀划分,并与主计算域平滑连接。主计算域由一组矩形网格单元划分,垂直方向靠近底面的最小网格尺寸为0.001m,水平方向为0.02m,总网格数为7.2×106。
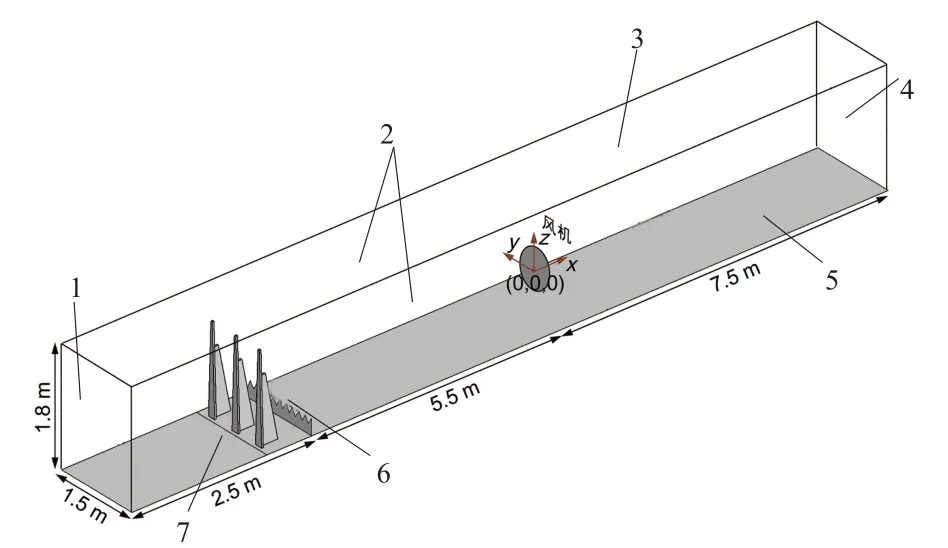
图2 计算域示意图Fig.2 Schematic diagram of calculation field
进风口采用均一流速度进口边界(velocity-inlet)条件,有u~=10m/s,∂p~/∂n=0;计算域底面、尖劈和围栏表面均采用壁面(wall)边界条件,有∂p~/∂n=0,u~i=0;计算域侧面以及顶面采用对称(symmetry)边界条件,在该边界处,有∂u~/∂n=∂v~/∂n=∂p~/∂n=0;出风口采用压力出口(Pressure-outlet)边界条件,此处有p~=0,∂u~i/∂n=0。
1.4 仿真结果
取y=0剖面,提取其轴向平均速度和脉动速度,其轴向平均速度云图与无量纲化后的风剖面如图3(a)所示、脉动速度云图与无量纲化脉动风速剖面如图3(b)所示,剖面位置分别为x=2D、4D、6D、8D。图3(a)可以看出,风经过风轮平面后,风速迅速降低,距离风机越远的位置处,风机对风场的扰动效果越弱。在风轮中心处,风速最小,向上向下逐渐增大,与实验变化趋势一致,数值仿真结果与实验值基本吻合。图3(b)可以看出,风经过风轮平面后,脉动风速值增加,距离风机越远的位置处,风机对风场的扰动效果减弱,脉动风速值减小。在叶尖高度处,脉动风速值最大,向上向下逐渐减小,与实验变化趋势一致,数值仿真结果与实验值基本吻合。

图3 尾流处速度场分布Fig.3 Velocity field distribution at wake
2 风机结构风致响应分析
2.1 运动方程
建立八自由度风力机模型,以简化旋转叶片与塔架耦合体系的动力响应计算。该风机模型基于广义坐标系,利用拉格朗日方程推导其动力学平衡方程。因风机在工作状态下,叶片保持旋转,机舱有时也产生偏航旋转,为描述该耦合体系,采用3套基准坐标系,如图4(b),(c)所示,X1坐标系固定于塔底,用于描述塔架的运动状态,其基向量为;X2坐标系固定于塔顶,用于描述机舱的运动状态,其基向量为;X3坐标系固定于叶片根部,并随叶片一起转动,用于描述叶片的运动状态,其基向量为时间t函数,可表示为。基向量均为顺风向,其余基向量均在风轮平面内。X1,X2坐标系各坐标轴互相平行,忽略主轴倾角及风轮锥角,将坐标系X1,X2绕y轴旋转ΨJ(t),可得X3坐标系。
八自由度风机模型坐标系示意图如图4所示,qJ(t)(J<3)表示三个叶片挥舞方向位移自由度,即挥舞方向一阶模态参与系数;qJ+3(t)(J<3)表示三个叶片摆振方向位移自由度,即摆振方向一阶模态参与系数。基于广义坐标系,在X3坐标系下,叶片J任意点的挥舞方向位移为uJ(r,t)和摆振位移vJ(r,t)可用下式表示:

图4 八自由度风机模型示意图Fig.4 Sketch of8-DOF wind turbine model

其中,Φ1J(r)为叶片J挥舞方向一阶模态;Φ2J(r)为叶片J摆振方向一阶模态,此处忽略轴向变形与扭转变形。同理,在X1坐标系下,塔架前后方向位移u(h,t)和左右方向位移v(h,t)可以表示为:
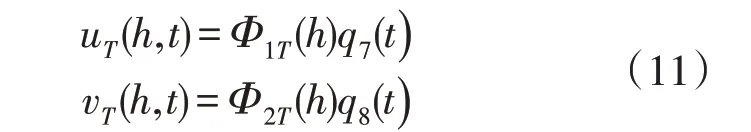
式中,Φ1T和Φ2T分别为塔架前后和左右一阶模态;q7和q8分别为前后和左右方向自由度,即对应的一阶模态参与系数。
考虑叶片J上一质点C,其速度向量为:

考虑塔体中所处高度为h的质点D,其位置矢量为:

则其速度矢量为:

风机体系的总动能为:

式中,M0为机舱总质量。
忽略扭转变形,对于叶片势能UJ,可分为弯曲势能UJ1、离心力势能UJ2与重力势能三两部分;塔架势能UT,主要分为弯曲势能UT1与重力势能UT2。

风机体系的总动能为:
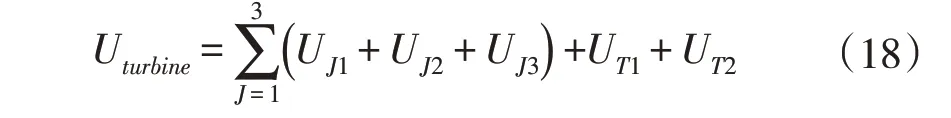
非保守力做功为:

应用非保守体系拉格朗日方程,

可推导其动力平衡方程为:

2.2 算例与验证
利用前述理论,编写陆上风机风致响应分析程序(AOWT)。该程序所包含的子程序,各子程序输入输出及其功能如表2所示,主程序框图如图5所示。

表2 子程序汇总Tab.2 Subroutine of subprogram

续表

图5AOWT程序框图Fig.5 Program chart for AOWT
利用该程序,对一台三叶片上风向风力机在湍流风场作用下的结构动力响应进行计算。该状态下,轮毂高度处的平均风速为10m/s,风剪切指数0.2,湍流强度为0.3,风轮转速10rpm。叶片内力时程如图6所示,塔底内力时程如图7所示,内力时程计算结果与商业程序Bladed相符,验证了本程序的可靠性。

图6 叶根内力时程对比Fig.6 Validation of internal force atblade root

图7 塔底内力时程Fig.7 Validation of interna lforceat tower base
3 工况设置
如文献[21]所述,因尾流风场平均速度降低,湍流强度增大,使下游风电机组载荷特性与上游风机有着显著区别,其疲劳荷载显著增大。本文计算工况与文献[21]一致,利用阻尼器进行各工况下振动控制,降低疲劳荷载。将下游风机放置于8个不同位置,其中4个为错列布置,4个为顺列布置。与上游风机间距分别为2D,4D,6D,8D。在错列布置中,下游风机与尾迹中心的展向距离为0.5D,各工况示意图如图8中所示。

图8 风机布置图Fig.8 Layout of the wind turbines
4 调谐质量阻尼器
4.1 TMD振动控制原理
将TMD控制系统放置于风机顶部机舱内,与机舱串联,以减小其风振效应。现考察TMD阻尼器对风机振动控制原理,其计算简图如图9所示。对于附加TMD阻尼器的风机结构,为描述体系运动状态,需外加质量块运动自由度qd,则:

图9 风机TMD控制结构构造图Fig.9 Wind turbine under TMD controller
TMD受控风机体系动能Td为:

势能Ud为:
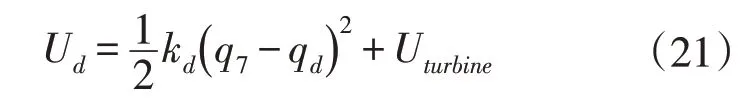
非保守力做功Wd为:
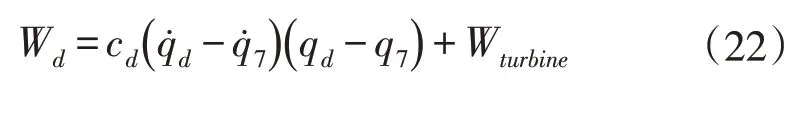
运用拉格朗日方程可得TMD控制体系运动方程为:

利用上式,修改前述第二章运动方程,添加TMD阻尼单元。
4.2 TMD参数优化
对于单自由度TMD控制体系,忽略了主结构阻尼影响,当外荷载为高斯白噪声时,可求解其理论最优解,如文献[22]所述。对于风机结构,所受外荷载激励复杂,尤其是处于下游的风电机组,尾流特性极其复杂。对于此体系,其TMD参数理论最优解无法获取。为与理论解对比,定义TMD质量系统质量比为,即质量块的物理质量与塔体一阶模态广义质量之比。本文采用数值检索方法,以塔顶位移方差σx为优化目标。
各工况下最优阻尼比、最优频率比随TMD质量比μ变化如图10和11中所示。从图中可看出,各工况下最优参数随质量比μ变化趋势大体一致,即最优频率比随质量比增大而减小,最优阻尼比随质量比增大而增大。除2DT、2DS、4DS工况外,其相对误差均在5%以内,在最优参数附近,目标值随参数变化较为缓慢,故最优频率比基本可按理论解取值。而对于阻尼比,仅有自由流和8DT工况下其相对误差较小,其余工况相对较大,超过20%,故对于其余工况下,TMD阻尼器最优阻尼参数应按数值解取值。

图10 最优频率比Fig.10 Optimal frequency ratio

图11 最优阻尼比Fig.11 Op tima ldam ping ratio
2DT工况下,取质量比为5%,TMD控制体系与无阻尼器塔底内力时程对比如图12所示,图中显示,TMD阻尼器减振效果显著,可降低尾流区风机结构疲劳荷载。质量比为5%的各工况下,TMD控制系统对等效疲劳载荷的影响如表3中所示,受控体系疲劳载荷显著降低,最优控制效果可将等效疲劳荷载降低50%左右。因前述TMD最优参数以塔顶速度均方根为优化目标,对等效疲劳荷载而言,并非一定为最优参数,故在某些工况下,其控制效果相对较差,等效疲劳荷载降低率仅有10%不到。
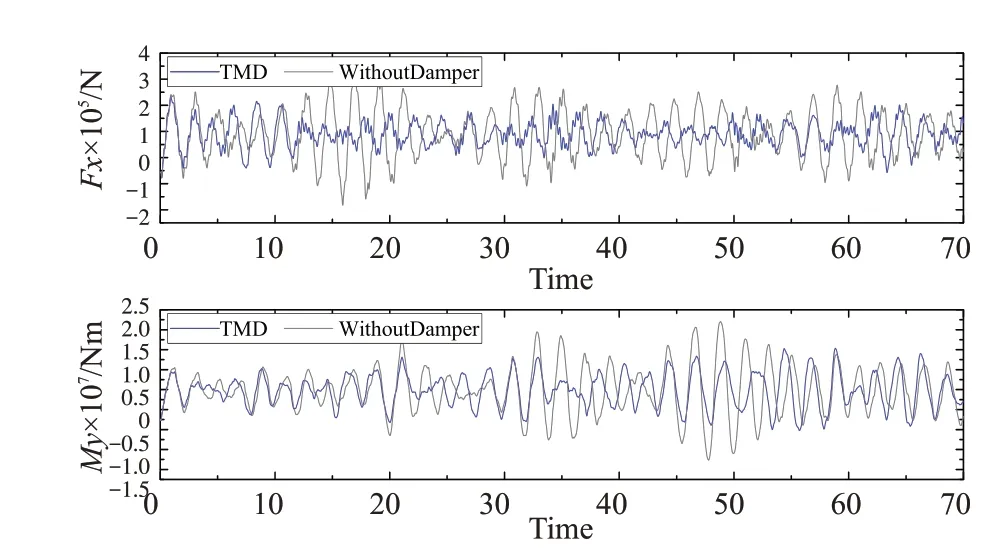
图12 TMD控制体系塔底内力时程对比Fig.12 Optimum dam ping ratio

表3 5%质量比等效疲劳载荷对比表Tab.3 Com parison table of equiva lent fatigue load with 5%m ass ratio
5 旋转惯性双调谐质量阻尼器
5.1 单自由度RIDTMD振动控制原理
为了提高TMD阻尼器减振效果,通常需加大TMD阻尼器质量。为改善TMD阻尼器,引入了旋转惯性质量装置,用于振动控制。该装置最早由Smith[23]提出,它能够将线运动转化为高速旋转运动,从而显著放大系统的物理质量。因此,它可以提供较大的惯性力,故被广泛用于土木工程结构[24-25]。该装置包含旋转惯性飞轮,其质量m1、转动惯量为J,弹簧k1、k2,阻尼c1基本单元,惯性飞轮与阻尼单元c1并联,与弹簧k2通过刚性底座串联,单自由度RIDTMD计算简图如图13所示。主结构位移为xs,质量块位移为x1,惯性飞轮底座位移为x2,主结构上作用外荷载F(t)。则:

图13 单自由度TIDTMD控制体系简图Fig.13 Sketch of1-DOFRIDTMD controlsystem
体系总动能为:
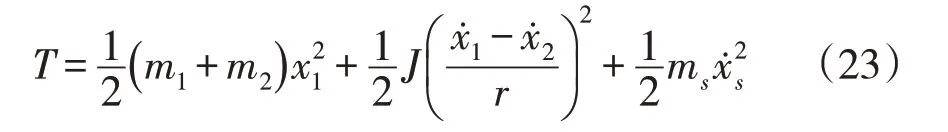
令阻尼器总质量mt=m1+m2,转动惯量J=βmtr2,上式可写为:
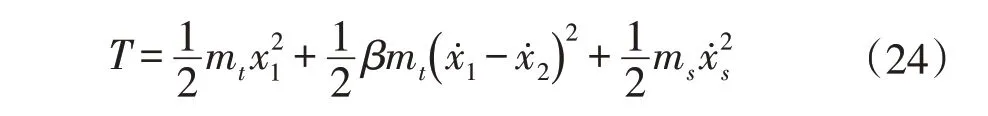
体系总势能为:
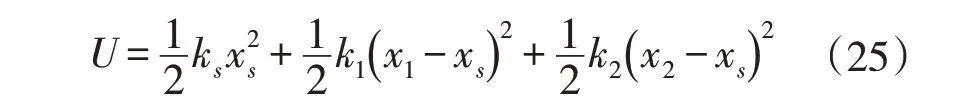
体系非保守力所做总虚功为:
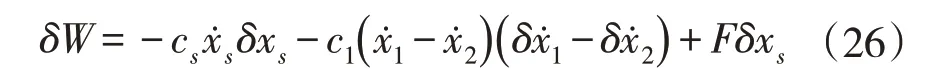
应用拉格朗日方程,可得其运动方程为:

令:


为进行结构动力响应的无量纲评估,定义动力放大系数为:

式中,Hs()ω为主结构位移频响应函数,详细表达式如文献[26]中所述。
对不同质量比μ条件下,分别按文献[22]、文献[26],取TMD与RIDTMD最优控制参数,主结构阻尼比取为0.02,保持两种阻尼器总质量一致。不同质量比μ条件下,动力放大系数随外荷载与主结构频率比ω/ωs变化如图14所示。图中SBTMD、SBRIDTMD分别表示TMD系统与RIDTMD系统控制频带,当外荷载位于此频带内,阻尼器可取良好的控制效果。图中表明,加大阻尼器质量比,对于动力放大系数最大值逐渐降低。且两类阻尼器控制频带显著加宽,故对于随机荷载作用下,其控制效果将随着质量比增加而增大。虽RIDTMD动力放大系数峰值大于TMD阻尼器,但当外荷载位于阻尼器控制频带内,RIDTMD控制效果明显优于TMD阻尼器。

图14 动力放大系数对比图Fig.14 Contrast diagram of DMF
5.2 风机结构RIDTMD振动控制
将RIDTMD阻尼器放置于风机机舱内,在旋转惯性质量装置内,小齿轮半径为rb,大齿轮半径为Rb,齿轮总质量为mb,总转动惯量为Jb。通过调节大小齿轮半径,可改变转动惯量Jb的值,如图15中所示。为描述风机受控直通运动状态,需额外附加质量块运动自由度x1,齿条运动自由度x2。

图15 风机RIDTMD控制体系Fig.15 Wind turbine with RIDTMD control system
则RIDTMD受控制风机体系总动能为:

体系势能为:

体系非保守力做虚功为:

运用拉格朗日方程可得风机结构RIDTMD运动方程:
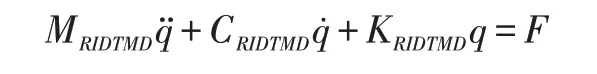
利用上式,修改第二章所述运动方程,添加RIDTMD阻尼单元。平衡方程将扩充为10自由度。
5.3 阻尼器参数优化与控制效果
采用MATLAB全局优化工具箱中的patternsearch算法[27]进行参数优化,在不同质量比μ情况下,以塔顶位移方差σx为优化目标。在不同工况下,RIDTMD最优参数(β,ν1,ν2,ξ)随质量比μ变化关系,与理论值对比如图16~19所示。图中表明,对于参数β,ν1,ν2,在自由流及其远尾流(x≥6D)作用下数值最优解与理论最优解基本一致,而在近尾流区域内差别较大。故在近尾流对于参数β,ν1,ν2应采用数值最优参数取值。各工况下,最优阻尼比数值解与理论解相差均较大,故对于参数ξ应采用数值最优参数。


图16 最优β对比Fig.16 Op timalβ
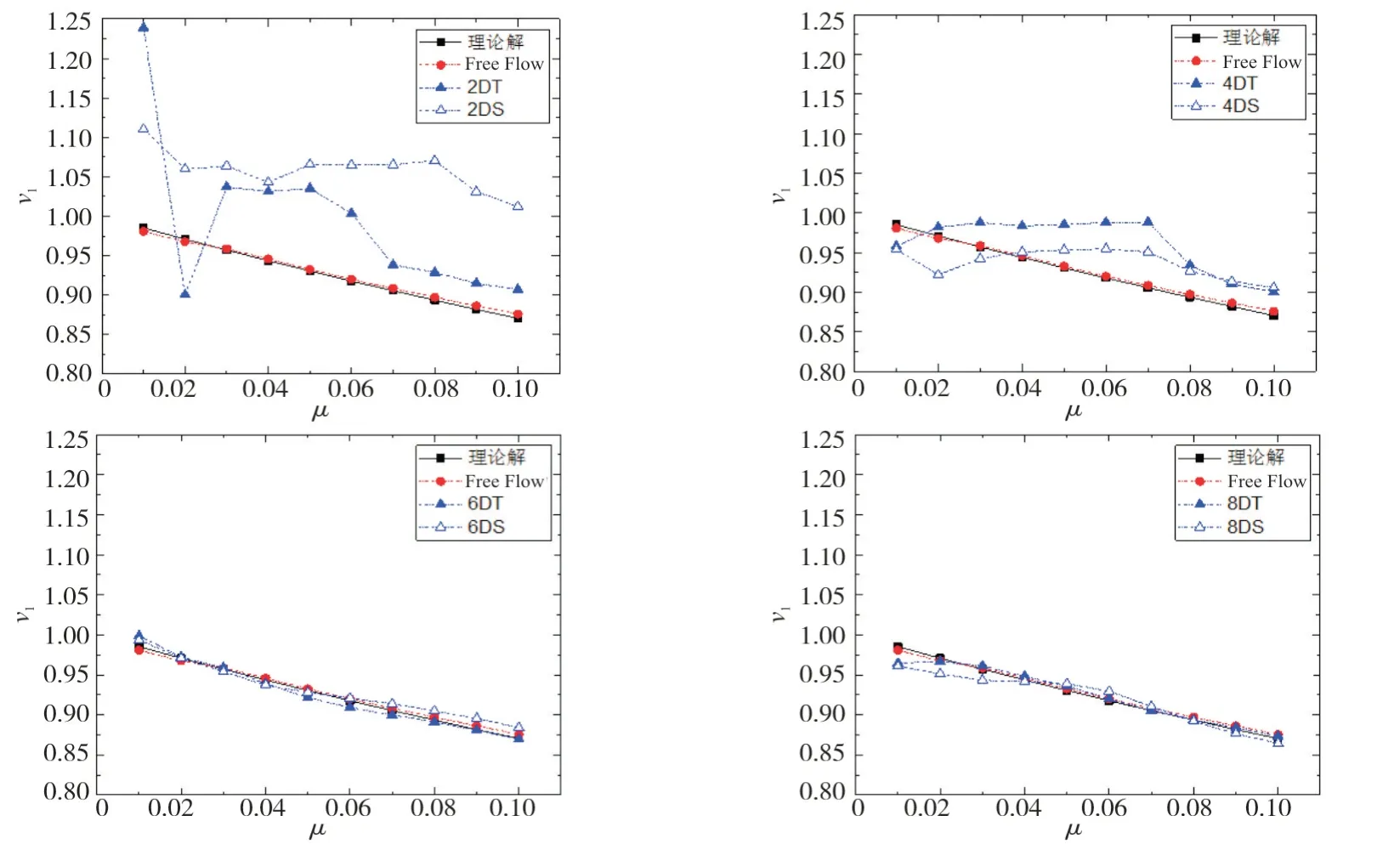
图17 最优ν1对比Fig.17 Optimalν1

图18 最优ν2对比Fig.18 Optima lν2

图19 最优ξ对比Fig.19 Optimalξ
取阻尼器质量比0.05,其余参数按上述数值最优解取值,2DT工况下塔底内力时程如图20所示。在不改变阻尼器总质量前提下,引入旋转惯性质量,可进一步降低风机振动响应,减小其等效疲劳荷载。

图20 塔底内力时程对比Fig.20 Comparison of internal force at towerbase
6 结论
本文主要开展了尾流作用下,下游风电机组振动控制研究工作。首先基于CFD模拟,采用了ALM方法进行了尾流风场的数值仿真;接着依据广义坐标理论,推导了考虑旋转叶片与塔体耦合时变体系的整机风机运动方程,利用C++程序语言,编制了陆上风机风致响应分析程序;最后采用TMD与引入旋转惯性质量的RIDTMD阻尼器对下游风电机组进行振动控制,对比分析了其减震效果。主要得到以下结论:
1)采用致动线方法获取的尾流风场数据与实验值相吻合,尾流风场呈现平均值降低,脉动值增大的特点;
2)所编制的陆上风机结构风致响应分析程序与商业程序Bladed计算结果吻合,该程序具有可读取任意风场数据、考虑旋转叶片与塔架耦合等特点;
3)引入TMD、RIDTMD阻尼器后,可降低下游风电机组的结构动力响应,在近尾流处,阻尼器参数与理论最优解差别较大,需按数值最优解取值。自由流作用下,其参数取值基本可按理论最优解取值;
4)利用TMD阻尼器,可极大降低下游风电机组等效疲劳荷载。在不改变阻尼器总质量的前提下,引入旋转惯性质量构成RIDTMD阻尼器可改进TMD阻尼器,使下游风电机组等效疲劳荷载进一步降低。

