风力机翼型多目标优化及尾缘加厚研究*
李志昂 王 军 尹国庆 王 威 彭 勇 覃万翔
(1.华中科技大学能源与动力工程学院;2.广东顺威精密塑料股份有限公司)
0 引言
翼型气动性能直接影响风力机的风能捕获能力。翼型优化设计方法可分为反设计方法和优化设计方法。反设计方法采用数学控制方程反推出满足目标速度或压力分布的翼型。优化设计方法直接以升阻力系数等翼型气动参数作为目标函数,在约束条件下,修正翼型几何形状及搜索目标函数极值来完成优化设计[1]。杨阳等[2]基于多目标遗传算法对风力机叶片进行优化设计,结果表明:优化设计后的叶片可以在叶片质量降低的条件下,提高封基里发电量。James Ferguson[3]等提出一种复合光滑曲面的函数表达方法;Hicks Henne[3]等将无粘空气动力学程序与共轭梯度优化算法相结合;Kulfan[5]等提出引入“形状函数”与“类函数”来描述翼型等任意的几何图形,极大地提高了翼型优化效率。
近年来,随着风力机不断发展,单机容量不断增大,考虑到风力机性能以及结构,对于钝尾缘翼型的研究也越来越多[6]。与具有相同最大厚度的尖尾缘翼型相比,在力学性能上,钝尾缘翼型具有更大的截面积以及更高的抗弯扭能力;在气动性能上,钝尾缘翼型具有更高的升力系数和失速攻角[7]。许多国内外学者在钝尾缘翼型加厚方法上进行了研究,Law SP等[8]采用直接截断法对翼型进行加厚,并且进行实验研究,发现钝尾缘翼型具有更佳的气动性能;Standish K J等[8]采用对称加厚法对尖尾缘翼型进行加厚,并进行数值分析;张磊等[10]通过非对称加厚法加厚翼型尾缘,结果表明:钝尾缘翼型使得风力机工作区向左移动;邓磊等[11]采用翼面刚性旋转法加厚翼型尾缘,并且对钝尾缘翼型气动性能进行模拟计算。
本文将翼型优化与钝尾缘技术相结合,采用多目标遗传算法与类别形状函数变换(CST)方法相耦合的方法对翼型外形进行多目标优化设计,采用指数混合函数方法对优化后的翼型尾缘进行非对称加厚处理,最大程度的提升翼型的气动性能。
1 研究对象和方法
NACA系列翼型具有较大的升力系数,较小的阻力系数以及桨距动量低的特点,其光滑的流线形状有利于进行参数化,在风力机中应用较多。选用相对厚度为18%的NACA4418翼型进行优化设计。
1.1 CST参数化方法
CST参数化方法使用一个类别函数C(x)和一个形状函数S(x)的乘积,再加上一个尾缘厚度项来表示一个尾缘不封闭的翼型。
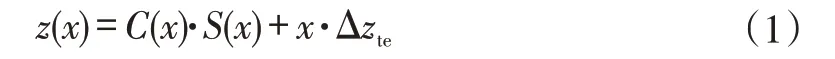
其中,类别函数定义为:

式中,N1和N2确定了所表示几何外形的类型,对于圆前缘尖尾缘翼型,分别取0.5和1.0。形状函数S(x)通常采用n阶Bernstein多项式来定义:

式中,Ki,n为型函数分量的组合数;bi(i=0,1,…,n)为权重因子,其值可由下式确定,

式中,Si(x)=C(xi)·Ki,n·(x)i(1-x)n-ixi∈(0,1),i=0,1,…,n
已知几何外形的控制点(xi,y(xi)),根据式(4)可验证CST参数化方法的单值性,参数化矩阵M和右端列向量Y的细微波动,会引起权重因子b的巨大变化,反之亦然。为了验证该参数化方法的准确性及精度,分别选择6,8,10,12个参数对NACA4418进行拟合,图1给出了不同参数个数的残差比较,可以看出P8和P12具有较高的准确度,P10在前缘处误差较大,可能是等距选取参数使前缘丢失某些点的特性。此外参数越多,占用的计算机资源越多,因此选择P8对翼型进行拟合。图2给出了8个参数时的CST参数化翼型与NACA4418翼型对比。
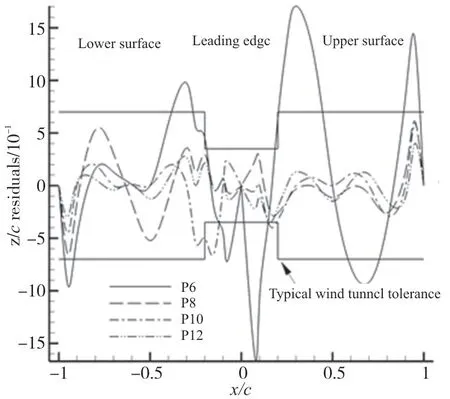
图1 不同参数个数的残差对比Fig.1 Comparison of residuals of different parameters

图2 P8参数化翼型与原始翼型对比Fig.2 Comparison of P8 airfoil and originalairfoil
1.2 指数混合函数方法
采用Standish K J等提出的指数混合函数法对翼型尾缘进行非对称加厚,采用幂函数分布来控制翼型尾缘厚度,保证了加厚翼型的几何连续性,设原始翼型的坐标为(x0,y0),加厚翼型的坐标为(x,y):
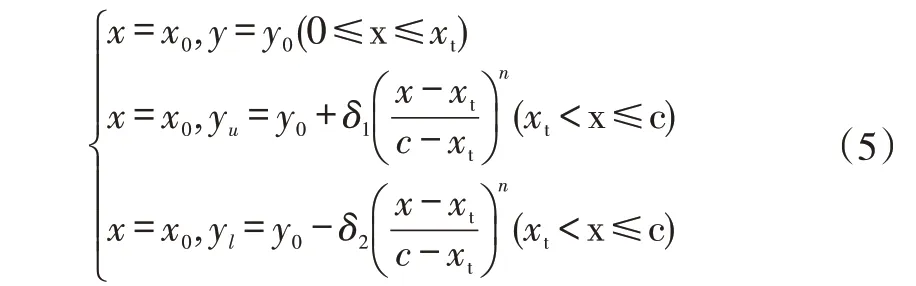
其中,xt为翼型最大相对厚度处位置;yu,yl分别为翼型上下表面坐标;δ1,δ2分别为翼型尾缘上下表面需要增加的厚度;c为弦长;n为幂指数,考虑到外形连续性及气动性能,取n=2。
1.3 数值方法与网格划分
翼型计算域和计算网格见图3。进口边界距翼型尾缘10倍弦长,出口边界距翼型尾缘20倍弦长。采用C型结构化四边形网格,网格节点分布为1024×85。对翼型周围网格做局部加密处理,网格总数约80000。

图3 翼型网格Fig.3 G rid diagram of NACA4418 airfoil
数值模拟采用FLUENT软件,采用稳态求解方法。本文来流雷诺数2×106,控制方程采用S-A单方程湍流模型,边界条件分别设置为速度进口和压力出口,离散方程采用有限体积法,扩散项采用中心差分格式,对流项采用误差更小的二阶迎风格式,速度和压力耦合采用SIMPLE算法,各项参数的残差小于10-5时认为计算收敛。
2 翼型多目标遗传算法优化
2.1 计算优化流程
对风力机翼型而言,升阻比是最重要的性能指标,其对于提高风力机运行效率和整个机组的性能影响重大。此外,保证翼型的高升力启动特性、平缓的失速特性也是风力机运行过程中很重要的环节。本文采用NSGA2遗传算法,将参数化建模,网格划分,CFD计算相耦合,生成翼型多目标优化的计算程序,图4为多目标优化设计流程图。

图4 多目标优化流程图Fig.4 Multi-objective optimizationm ethodo logy
选取6°攻角运行时的升阻比最大,2°低攻角下的升力系数最大,以及17o近失速攻角下的阻力系数最小为优化目标。以6o攻角时的升力系数不小于0.97为约束。翼型多目标优化问题可表示为:

约束条件:Cl6≥。为原始翼型在6o攻角下的升力系数,为0.97;Cl,Cd后的数字分别表示对应的运行攻角。
优化变量:依据CST参数化方法,共有8个优化变量,分别为上表面控制因子,b0,u,b1,u,b2,u,b3,u以及下表面控制因子b0,l,b1,l,b2,l,b3,l。变量范围设置为原始翼型控制变量数值上下20%,具体数值见表1。

表1 优化变量取值范围Tab.1 Disturbance range of optimization variables for CST method
遗传算法参数:种群规模数为50,进化代数为40,杂交概率为0.7,变异概率为0.1,变量采用实数编码。
2.2 优化结果与分析
图5(a)所示为多目标优化种群分布图,初始种群分布散乱,随着进化代数的增加,升力系数Cl与升阻比Cl/Cd增大,阻力系数Cd不断减小。
如图5(b)所示,从pareto解集中选取一组方案进行数值计算分析并与原始翼型进行对比。图中所示方案在任一优化目标数值上并无明显优势,但是综合考虑3个优化目标时,该方案具有一定的优势,所以选取图示方案与原始翼型进行对比。
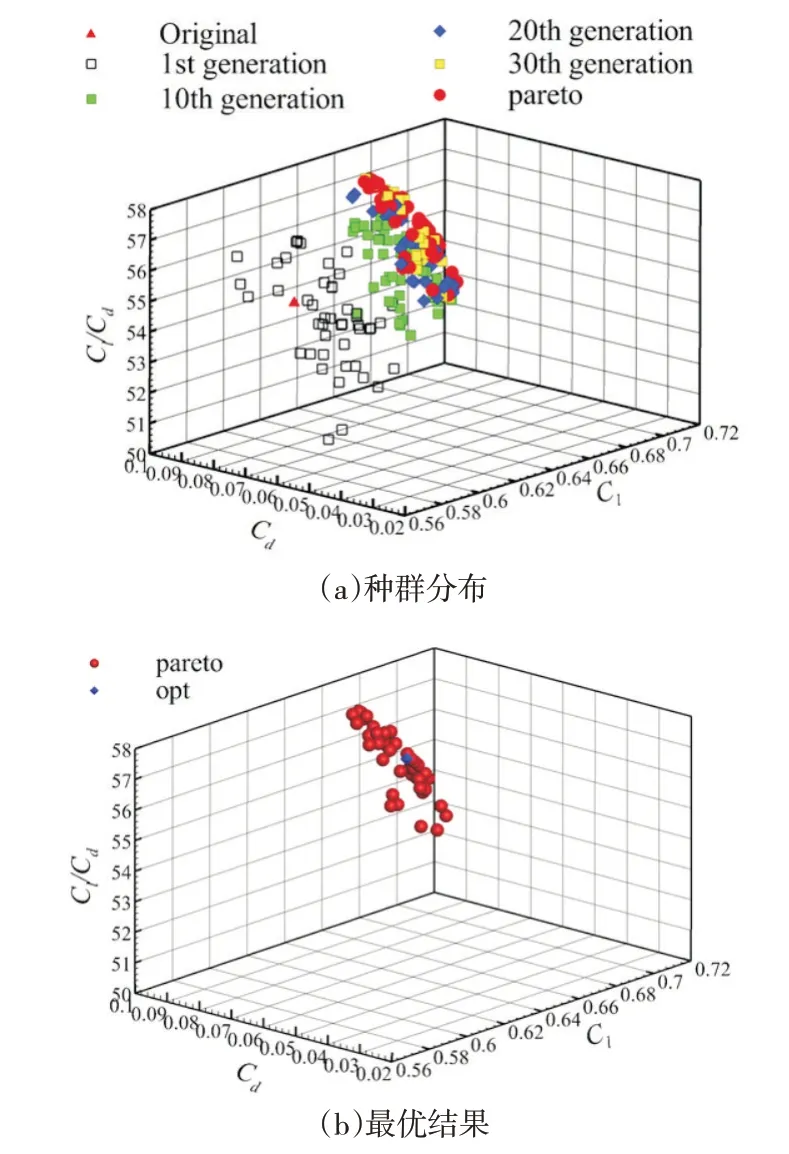
图5 多目标优化种群分布Fig.5 Population distributions of multi-objective optimization
对满足Pareto最优解的翼型进一步在0°~17°攻角下进行数值计算,选取其中一组进行分析,变量参数值如表2所示。优化翼型外形轮廓比较如图6所示,优化翼型与原始翼型在上表面结构差别不大,主要改变是前缘半径减小,翼型弯度增大,上表面外凸,下表面内凹,翼型最大厚度有所减小。

表2 优化翼型变量参数值Tab.2 The parameters of the optimized airfoil

图6 优化翼型与初始翼型外形比较Fig.6 Com parison of shape between the optimized airfoil and original airfoil
图7为压力系数比较图,可以看出上表面前段压力系数有所下降,后段与原始翼型基本保持一致,下表面压力系数增加,总的来说翼型上下表面压力差增大,导致翼型升力系数增大。
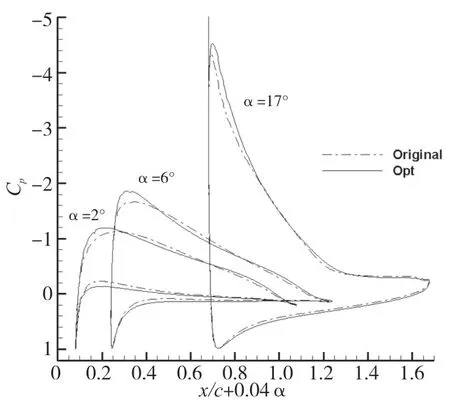
图7 优化翼型与初始翼型压力系数比较Fig.7 Com parison of pressure coefficients between the optimized airfoiland the originalairfoil
图8和图9为升阻比及升力系数对比图,可以看出在设计工况和非设计工况,翼型的升阻比及升力系数均有所提升,尤其是在2°攻角下,升力系数和升阻比分别提升了12.36%和12.20%,此外,大攻角下的阻力系数也下降了6.21%,其它运行工况下的升阻比系数也有不同程度的提高。这说明优化的翼型具有良好的运行效率及平缓的失速性能。

图8 优化翼型与初始翼型升阻比系数比较Fig.8 Comparison of lift-to-drag ratio between the optimized airfoiland the originalairfoil
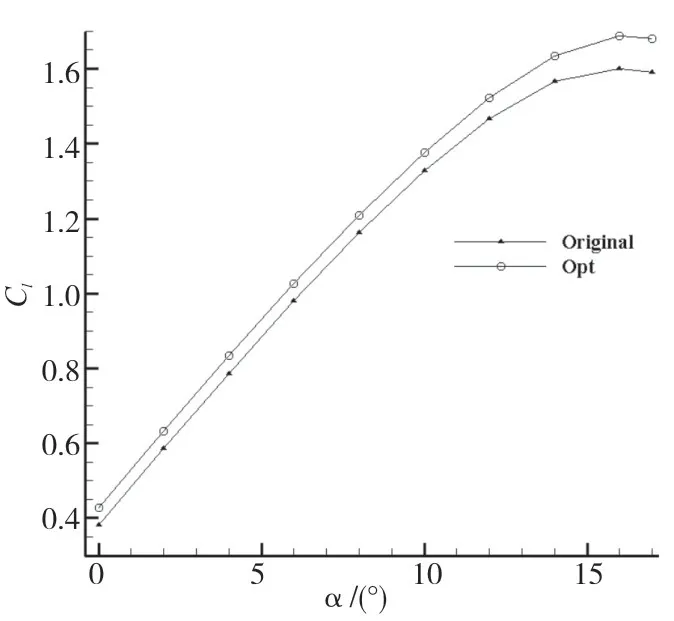
图9 优化翼型与初始翼型升力系数比较Fig.9 Comparison of liftcoeffi cientbet ween optimized airfoiland the origina lairfoil
3 翼型尾缘加厚优化
采用式(5)所示方法对Opt翼型尾缘进行加厚处理,尾缘加厚厚度为优化变量,以不超过0.05c为约束条件,由于变量较少,故采用正交试验法建立16组变量优化空间,考察翼型在0°~17°攻角下的升力系数及升阻比,选取一组升阻比及升力系数均有显著提升的翼型进行研究。加厚翼型与原始翼型外形对比如图10所示,翼型前半部分没有变化,后半部分翼型平缓过渡,尾缘上表面增加0.01c,下表面增加0.005c。
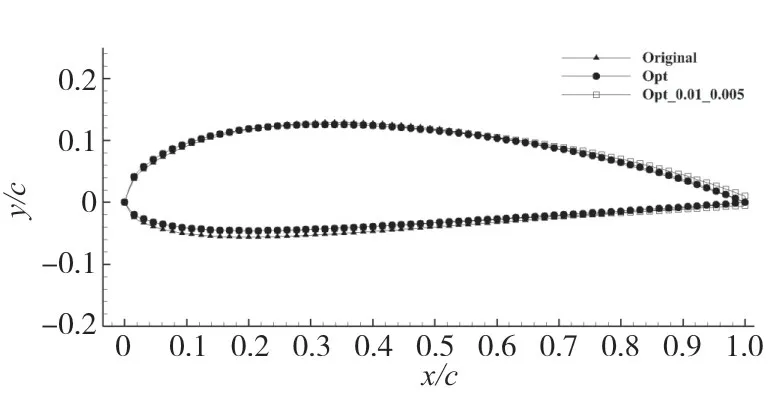
图10 两种优化翼型与初始翼型外形比较Fig.10 Comparison of the shape of two optimized airfoils and the originalairfoil
图11为压力系数比较图,钝尾缘优化后上下表面压力系数与Opt翼型在前半段基本一致,靠近尾缘部分,后翼型上表面压力系数更小,下表面压力系数更大,上下表面压力差增大,升力系数进一步增大。图12和图13为升阻比及升力系数对比图,可以看出钝尾缘翼型在所有工况下都要比Opt翼型好,相较原始翼型,在2°攻角,升力系数和升阻比分别提升23.55%和19.01%,17°攻角下的阻力系数减小了8.91%。钝尾缘翼型升阻力特性要优于原始翼型和Opt翼型。

图11 两种优化翼型与初始翼型压力系数比较Fig.11 Comparison of pressure coefficients between two optimized airfoils and the originalairfoil

图12 两种优化翼型与初始翼型升阻比系数比较Fig.12 Comparison of lift-to-drag ratio between two optimized airfoils and the originalairfoil

图13 两种优化翼型与初始翼型升力系数比较Fig.13 Comparison of lift coe fficientbetween two optimized airfoils and the originalairfoil
图14是三种翼型在不同攻角下的流线比较。由图14(a)可以看出,在14o攻角下,钝尾缘翼型的涡心位置要比原始翼型和Opt翼型靠后,且经过优化,翼型的分离点相较原始翼型后移了11.4%,涡结构也有所减小。图14(b)中,17o攻角为近失速攻角,相较14o攻角,涡心位置和分离点均前移,此时流动状况变得复杂,流动分离现象更加明显,翼型面临失速的风险。相较原始翼型,翼型经过优化和加厚处理后,其分离点和涡心位置分别后移了13.7%和3.4%,从流动层面解释了翼型升力系数的变化趋势。翼型的流线图表明该优化方案改善了翼型表面的流动状况,减缓了边界层的分离。


图14 三种翼型在不同攻角下的流线比较Fig.14 Stream lines of three airfoils atdifferentang le of attack
4 结论
本文将翼型遗传算法优化与钝尾缘技术结合起来,获得了气动性能具有很大提升的优化翼型及钝尾缘翼型。
1)将多目标遗传算法运用到风力机翼型的性能优化中,可节省翼型优化设计时间,同时能够得到一系列性能良好的翼型。
2)钝尾缘翼型的升力系数普遍要高于同工况下相同厚度的尖尾缘翼型,但阻力系数也会有一定程度的增加,尤其是在大攻角下,升阻力系数可能会出现不及原始翼型的情况。
3)翼型经过整体优化和钝尾缘加厚处理后,其分离点和涡心位置均后移,且涡结构有不同程度的减小,改善了翼型表面的流动状况,推迟了边界层的分离。

