基于机器学习聚类算法的水平井流型预测
*卢鑫 牛月
(长江大学地球物理与石油资源学院 湖北 430100)
1.引言
对于国内外各大油气田来说,测井前的测井方案设计是极为重要的环节,方案设计中包含对测井仪器的选取、产能预测以及井下流体流型判定等。在油田开展井下作业前,对井下流体流型进行预测是非常有必要的一项工作,通过对井下流型进行合理判断,能够有利于工程师制定科学有效的测井方案以及更加合理的仪器组合,有效的减少了人力物力消耗。
随着信息技术的发展计算机技术也在不断更新换代,机器学习发展也得到了极大的支撑,国内外利用机器学习已经发展成熟的渗透率预测以及岩性识别[2]等也给测井行业数据处理提供了新思路。同时测井知识与机器学习算法相结合,不仅能够促进智能地球物理事业发展,也能为后续生产测井中的产能预测提供理论支撑。
2.算法原理
(1)聚类算法
聚类算法(K聚类算法[3])基本原理如下:假定给定的数据样本X,包含n个数据对象集X={X1,...,Xn},其中每个数据对象都具有m维度的数据,在这里可以每个数据对象理解为矩阵中的向量。算法目标是将n个数据集,根据数据之间的相似性聚集到指定的个类别中去,数据集合中的每个数据仅仅只属于一个已经确定好的类簇,也就是说不会存在一个数据属于多个类别的情况。
聚类算法的步骤如下,首先需要初始化k个聚类中心{Center1,...,Centerk},然后通过计算每一个数据到每个中心点的距离,距离公式如下:

式中,Xi表示第i组数据(1≤i≤n);Centerj表示第j个聚类中心(1≤i≤k);Xit表示第i组数据中的第t个数据(1≤i≤m,m为数据的纬度)。
依次比较对象到聚类中心点的距离,将数据对象分配到距离最近的聚类中心点的类别中去,在处理完所有数据之后,就能得到一个含有k个类别的集合{Class1,...,Classk}。聚类算法用聚类中心来定义类簇,聚类中心就是每个类别内所有数据对象在各个维度的均值,计算公式如下:

式中,Centeri表示第i个聚类的中心点(1≤i≤k);|NClassi|表示属于第i个类别中数据的个数;Xi表示第i个类别中的第i个数据。
通过不断对聚类中心点进行更新,直至算法达到结束条件,算法结束条件如下:
①数据集合中所有数据不再被重新分配给不同的数据类别中去;
②多次对数据进行分类后,原有数据中心点不再发生变化;
③所有数据点都被访问完毕,但依旧没有找到合适数据中心点。
(2)数据降维
由于聚类算法处理的数值为二维数据(坐标系中常以点的形式呈现),对于测井数据而言,往往数据是多维的,井筒单层界面包含诸多需要考虑的因素,例如含水率、含油率、温度、井筒内液体流速度以及管柱结构等。在本文中能够由实验室模拟且参与计算的数据依次为:流体流速、井斜、含水率、温度以及井径。五组数据如何利用聚类算法进行数据分析,那么针对诸多数据首要的工作就是数据处理,数据处理包括对数据离散点的剔除以及数据降低维度,从而使得所有实验所得数据在不丢失关键信息的情况下,能够达到算法能够处理的数据规格。这里可以参照线性代数中求取矩阵特征值的方法,将测井数据假定为维度为N的矩阵,利用多维数据计算出来的特征值来代替原有的多维数据。
在数据线性变换过程中,可以从几何的角度来理解,针对三维直角坐标系而言,数据在三维坐标系中的每一个系都会存在点到面上的投影,线性变换的过程就是求取投影点的过程,主要步骤为以下两点:①重新确定单位向量,如公式1中的单位向量Y=[y1,...,yN]T以及X=[x1,...,xN]T,N为矩阵的维度;②将原始样本集所表示的向量在新的单位向量上投影。

对利用公式1求出来的所有单位向量进行均值(公式2)以及方差(公式3)计算,选取最小的方差数据组合,同时将所求的单位向量假定为所有数据的最合适的近似二维坐标,从而达到数据降维的目的同时也便于后续聚类算法对数据进行分类。
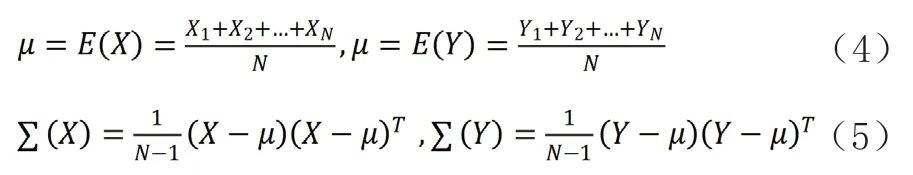
式中,X1为求出来的第1组X轴单位向量;Y1为求出来的第1组Y轴单位向量;μ为均值;Σ(X)以及Σ(Y)代表所求的XY轴数据的方差。
然而上述式中所设定的数据矩阵必须是数据个数等于数据维度,这对于测井行业来说是不现实的,在测井行业中数据分数往往大于或者是远大于数据维度,因此必须找寻一种能够代替矩阵的计算方法,此方法必须能兼备数据降维以及保存数据信息。这里就可以参考机器学习中的数据降维方法,通过对本文所用到的实验测井数据进行分析之后,发现PCA降维方法针对此测井数据类型的数据处理是最合适的。
主成分分析法(Principal Component Analysis,PCA):主成分分析法主要应用于具有连续属性的高维数据集,是一种较为常见的数据分析方法。此方法通过线性变换变化将原始高维数据变化为低维数据向量,且数据向量集合中必须包含整体数据的大部分数据特征。
PCA降维方法的整体降维步骤如下:
①首先将数据集合整体视为一个初始数据矩阵,如下式:

式中,X为整体数据矩阵;x11,...,Xnp整体数据集合中的每一个数据;X1为第一列数据向量集合;Xp为第p列数据向量集合。
②将数据矩阵以列为单位进行标准化处理,标准化处理后的的数据矩阵仍为X;
③标准化处理完成之后,求矩阵中每个元素的相关系数,同时构建为一个p×p的数据矩阵C=(coeij)p×p,其中每个元素相关系数的计算公式如下;

其中coeij=coeji,coeii=1。
④构建矩阵的特征方程,求出矩阵特征值;

其中式中λ大于0。
⑤确定矩阵主成分个数;

式中的α一般被称为数据贡献率,主要是用来衡量当前数据对于整体数据分析的重要性,在计算中当某一数据的α大于80%时,我们一般称此数据为不可丢失数据。
⑥计算n个向量对应的单位特征向量;
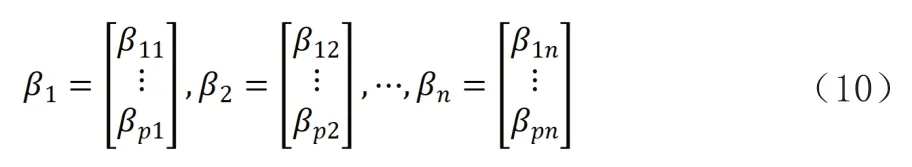
⑦计算每列数据主成分。

通过上述步骤即可将矩阵为n×p的高维数据集合降低为一维数据向量集合,针对测井数据的降低维度我们设置了两种数据规格—影响因素大于某阈值的设置为x轴坐标,影响因素小于某阈值的设置为y轴坐标,至此完成了整个高维数据降维的过程。在实际数据分析测试中,未降维的数据集合数据预测准确率在75%-80%之间,而利用PCA降维后的数据集合进行数据预测整体准确率在83%以上,同时极大的较少了数据分析时间。
3.方法应用
首先利用聚类算法随机在数据集中选取3个不重复的中心点(本节中假定需要分析的测井数据最终结果为3种流型),分类过程如下,首先确定第一个中心点Center1,中心点选取完成之后不断地计算中心点到其他点之间的距离之和S1;同时选取另外一个随机中心点Center2,并且计算这个中心点到其他点之间的距离之和S2,比较两者之间的大小,如果S1大于S2,此时第一个大类的中心点由Center1变为 Center2;反之,数据中心点不变。通过不断的重复上述步骤,直到所有的点都参与了分类计算过程,聚类算法结束。
通过上述描述可以发现实际聚类算法只是单纯为数据分类,在实际测井作业中,工程师更想看到的为图、表格、坐标系或者文本展示分类结果。例如在直角坐标系中,对于不同类别的数据点我们可以设置不同的颜色并标识出他们的中心点,这样就真正实现了聚类算法的数据可视化。
图1(a)、图1(b)为分类结果以坐标系形式展示示意图,图1(a)为数据整体的直角坐标系,图1(b)为分好类别后的直角坐标系,图1(b)中五角星标识为数据中心点。通过对比两张图版可以发现,针对庞大的数据集机器学习聚类算法的分类效果非常理想。
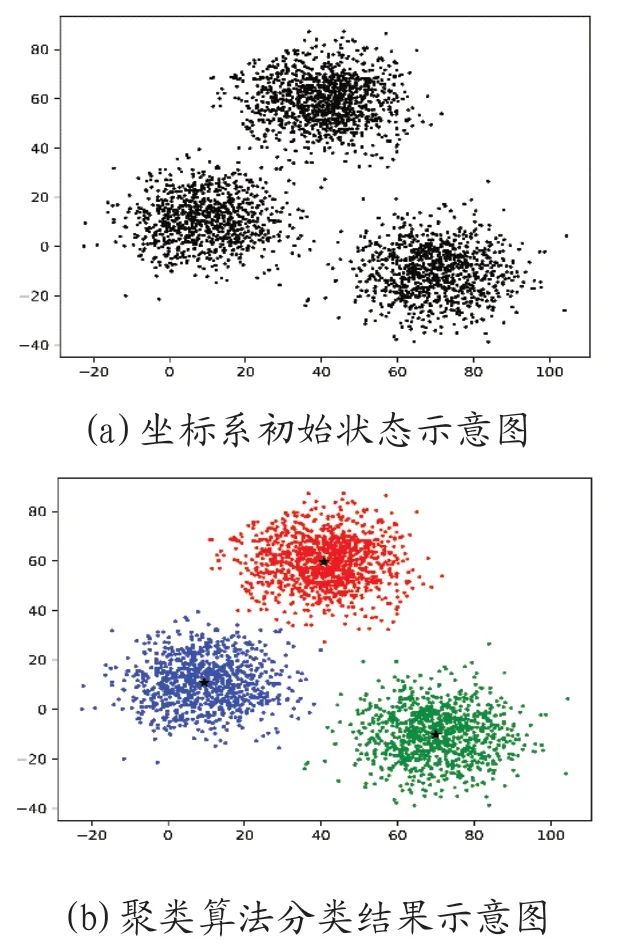
图1
4.实验
(1)设计实验
本次实验将数据分为算法训练数据以及实际测试数据两大类,训练数据用于算法构建预测模型,测试数据中的各项数据将被用来当作算法计算值,并对数据进行流体流型预测。最后将算法得到的预测流体流型同实际流体流型进行对比,从而达到检验算法的准确性。
通过对实验所测出的数据进行数据分析,通常测试数据中包含的数据有:流量、井斜、井径、温度、管径及含水。检测数据预测准确性的方法大致为以下两种方式:
①对现有实验数据,将预测结果同实验结果进行对照;
②对实验尚未测量数据,按照生产测井导论中的流型模型图来进行对照。
通过分析算法在不同流量、不同含水以及不同井斜时的准确度,来判定算法是否适合井下流体流型预测,同时也能判断出算法的可行性。
(2)预测结果分析
在算法整体过程结束之后,选取流量为600m3/d预测结果数据中井斜为0°、60°、85°、90°(含水数据对应为20%、40%、40%、90%)的四组数据,随后以同样的方式选取流量为300m3/d及100m3/d预测结果的四组数据共组成12组数据,将所选12组数据流体流型预测结果与实验真实结果进行对比,从而验证聚类算法针对流型预测准确率,具体信息如表1所示。
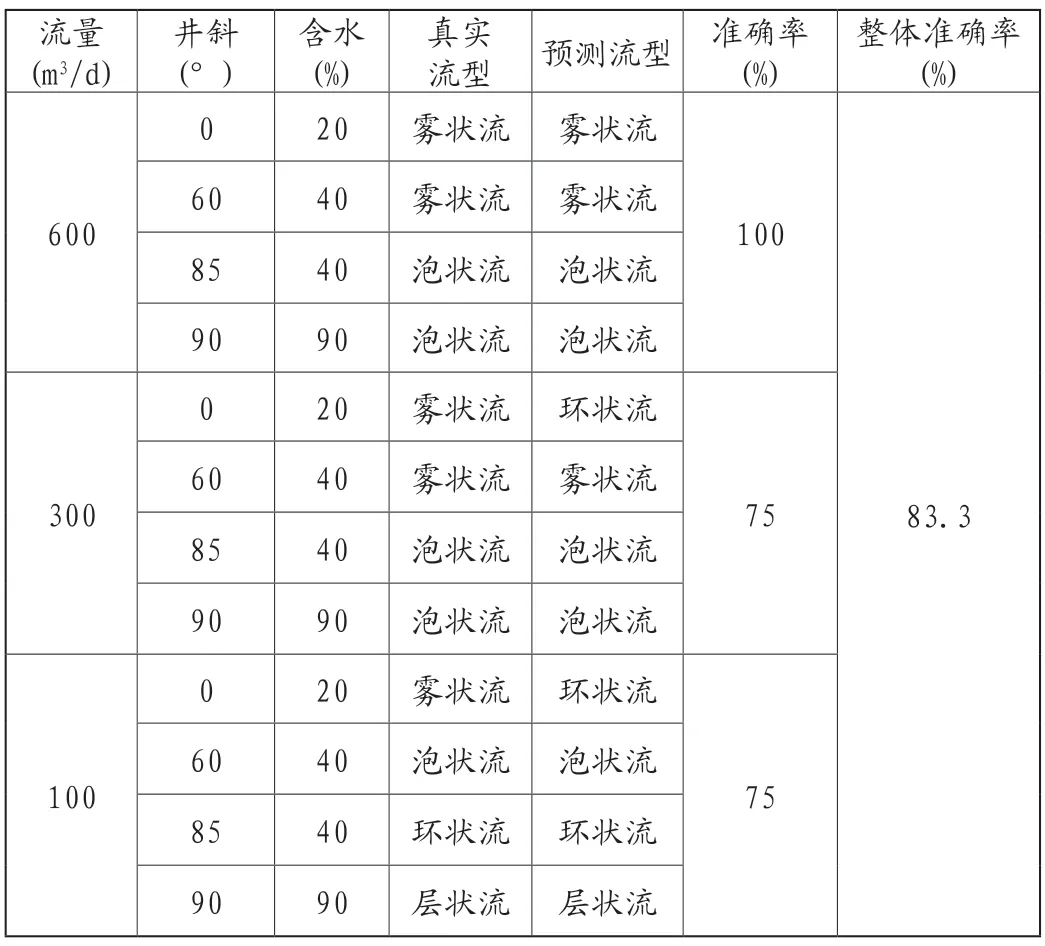
表1 算法预测结果同真实结果对比
由表1中可以得出,在流体大流量时算法针对数据预测结果相较于小流量时准确度有大幅度提升,在小流量以及垂直井或近垂直井时对流体流型的预测准确度较低,因此该算法在大流量水平井中比较适用。(注:井斜为90°指水平井,井斜为0°指垂直井)
5.结论
通过将机器学习算法预测得到的流体流型同实际流体流型对比,并对数据的准确率以及消耗时间进行分析可以得出如下结论:
(1)通过利用机器学习算法聚类算法进行井筒流体流型预测,提供了流体流型预测的新思路;
(2)利用合适的降维方法对高维数据进行预处理,在保证的数据信息完整的情况下对数据进行批量降维,降低了计算机处理数据的难度,提高了方法对处理数据的效率;
(3)通过选取合适的测井资料作为数据库,能使算法对井下流体流型预测结果更加准确,算法为后续预测水淹层情况提供了新思路,具有较高研究价值;
(4)后续可对算法进行不断优化同时建立合适的数据模型,从而提高算法准确度值并扩大算法适用范围。

