高速低载频比下电流型逆变器有源阻尼策略研究

王晓琳， 王强， 鲍旭聪

(南京航空航天大学 自动化学院，江苏 南京 211106)

0 引 言

高速电机具有能量密度大、体积小等优点[1-2]，在飞轮电池、离心压缩机和小型电主轴等需要高速直驱动力源的场合有着广泛的应用[3-4]。长期以来，电压型逆变器一直是电机驱动器的研究重点，然而，电流型逆变器电流特性良好[5]，且具有升压特性，十分适用于驱动高速电机。电流型逆变器的直流侧以电感作为储能元件，相比于电压源型逆变器电容储能方案可靠性高，随着磁性材料技术的发展，尤其是超导材料的发展，电流型逆变器存在更广阔的发展空间[6]。

电流型逆变器由于滤波换相电容的存在，其交流侧呈现为二阶特性，在谐振频率处电流环幅频响应存在尖峰，同时相位会发生负180°跳变，这容易造成逆变器系统震荡甚至不稳定，因此，必须提高系统阻尼系数[7]。常用阻尼策略分为无源阻尼和有源阻尼。无源阻尼策略通过在拓扑中增加电阻来提高阻尼系数，该方法已得到广泛应用，但无论使用何种连接方式，总有电流流经阻尼电阻，系统存在额外的功率损耗，效率低下[8]。无源阻尼策略则通过改变控制回路以提高系统阻尼，主要分为反馈型有源阻尼及滤波器型有源阻尼[9]。反馈型有源阻尼通过额外的电压传感器引入了电压反馈内环，实时抑制谐振尖峰，理想情况下能够实现和无源阻尼相同的效果[10]。滤波器型有源阻尼在电流环前向通道中插入一陷波器，通过削弱电流矢量中谐振频次分量的方法实现提升阻尼系数的目的[11]。

在实际控制系统中，受限于数字信号处理器的性能，高速电机运行于低载频比状态，控制延迟对电流环性能影响增大。文献[12]建立了电压型逆变器基于复系数传递函数的电流环控制模型，在此基础上分析了高速低载频比下电流环失稳的原因，提出了一种带角度误差补偿的复系数PI控制器，实现了对拖平台在高速低载频比时的稳定运行。数字控制系统中，有源阻尼策略在改变控制回路的同时会将控制延迟引入系统，这会造成有源阻尼策略的失效。针对该问题的研究集中在LCL并网逆变方向，文献[13-14]分析了电容电流反馈有源阻尼受控制延迟影响时并网逆变器出现不稳定的原因，并通过电容电流的即时采样与反馈系数优化设计增大了系统稳定裕度，保证了并网逆变器的正常运行。

本文针对电流型逆变器驱动的高速永磁同步电机，利用复矢量将其交流侧微分方程化简为单状态变量表达式，并对高速低载频比下数字控制延迟及其引入的角度误差对系统造成的影响进行定量分析，构建数字控制电流型逆变器电流环模型。针对谐振尖峰的问题，本文分析对比反馈型有源阻尼及滤波器型有源阻尼，对二者作用机理进行统一。在考虑数字控制延迟时，本文通过对控制回路各环节Bode图的分析，得出反馈型有源阻尼不适合本文设计的电流型逆变器的结论，并提出带角度误差补偿的陷波器的设计方法，实现电流环在高速低载频比下的稳定运行。对电机耦合项引起的谐振尖峰偏移，通过构建中间函数指出分段陷波控制的设计方法，解决电流环性能受电流基频影响的问题。

1 数字控制电流型逆变器

1.1 基于电流型逆变器的永磁电机复矢量模型

电流型逆变器电路拓扑如图1所示，直流侧由电流源供电，经由电感Ldc滤波后输入逆变桥；逆变桥中开关管顺向串联二极管以保证反向阻断能力；滤波电容C在滤除开关频率及其整数倍谐波的同时，在换流时吸收电机电感中存储的能量。下标w、c、s分别表示逆变器侧、电容端及定子侧电气参数，附加项为受角速度ω影响的反电势扰动。

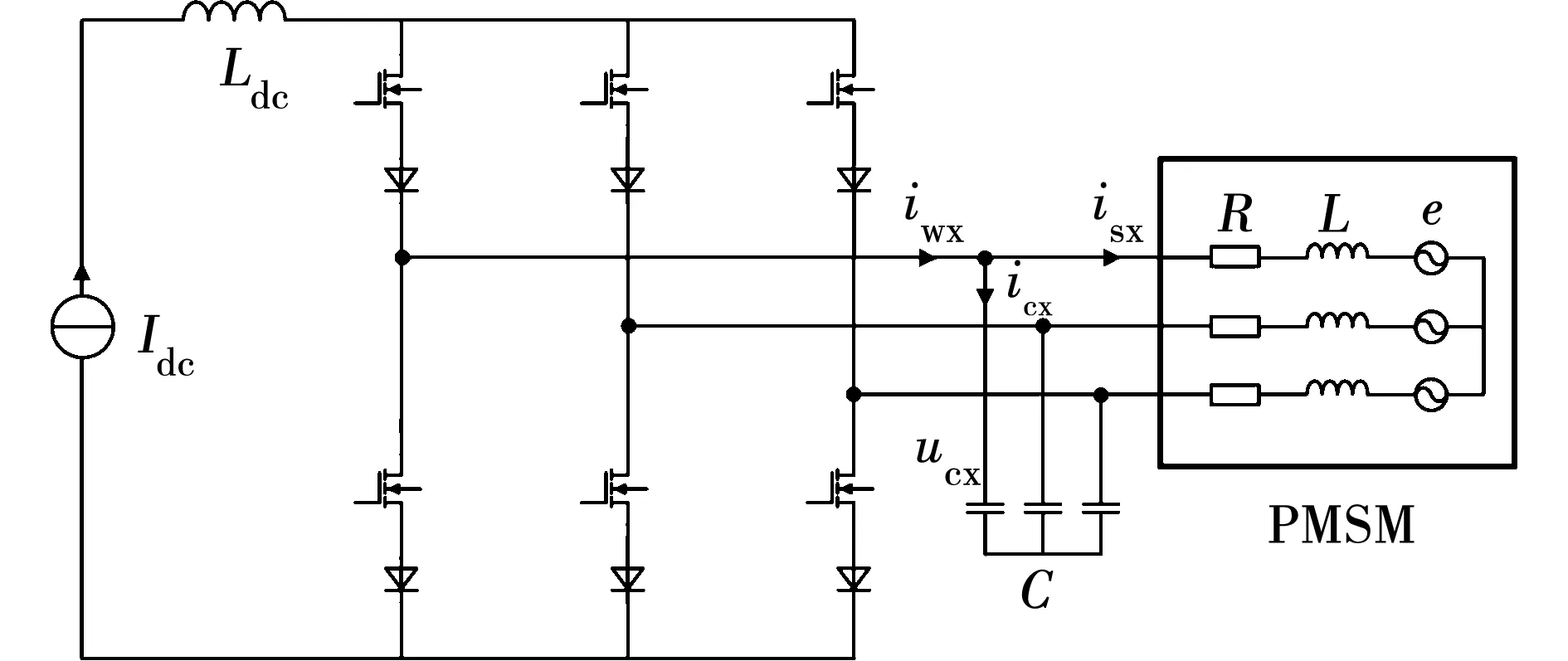
图1 电流型逆变器电路拓扑Fig.1 Topology of curent source inverter

基于矢量控制的电流型逆变器交流侧d-q坐标系下的状态方程为

(1)

从式(1)可以看出，电流型逆变器驱动的永磁同步电机是一个耦合的双输入双输出系统，采用复矢量模型可以在表征耦合项的同时使用经典控制理论对其进行分析。经推导可得到基于复矢量的交流侧微分表达式为

(2)

由此绘制电流型逆变器交流侧结构图如图2所示，其中i，u分别表示电流及电压复矢量。

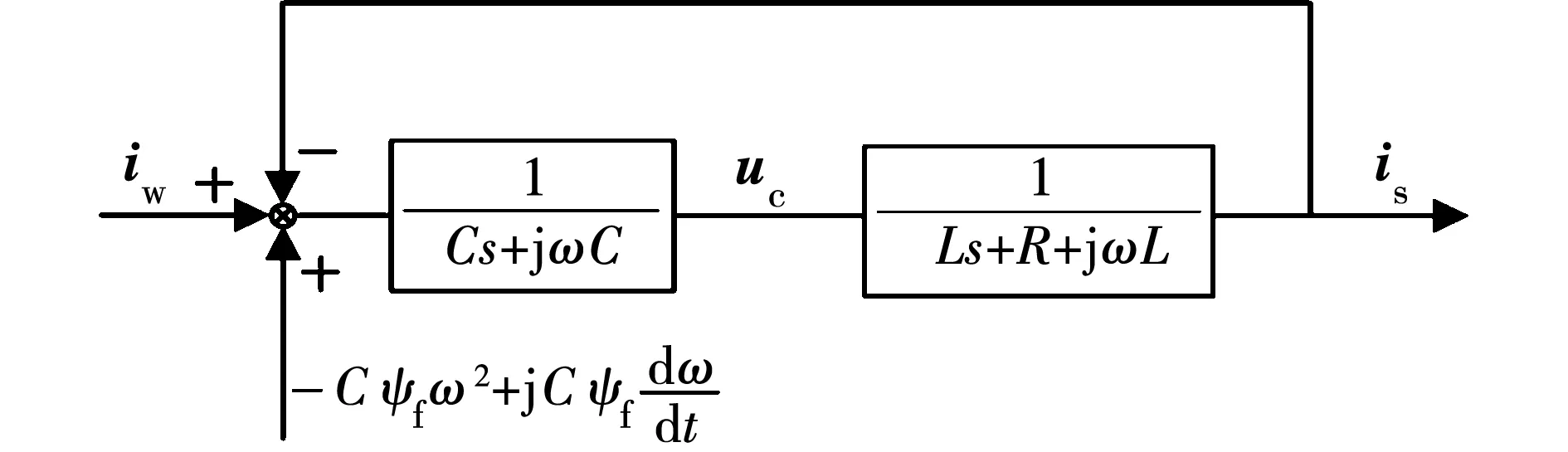
图2 基于复矢量的交流侧结构图Fig.2 Structure diagram of AC side based on complex vector

1.2 数字控制电流环建模

采用数字控制器实现电机的闭环控制时，电流环内存在一拍固有延迟Z-1；占空比在装载后一个周期内保持不变，等效为零阶保持器(zero-order holder，ZOH)，以上二者共同构成了时间延迟。在采样到占空比装载这段时间内，电机仍在运行，电机实际电角度将超前反帕克变换时使用的电角度，这将导致期望电流矢量与输出电流矢量存在角度误差，可表示为

(3)

式中：θ，is为采样时刻电机电角度及电流矢量幅值；T为控制周期。随着转速的升高，角度误差θd=1.5ωT对系统影响逐渐增大。电机在额定转速且控制频率设定为100 kHz时，电流矢量存在49.5°的角度误差，该角度误差将在开环相频响应中造成相同数值的相位跌落，对电流环性能造成严重影响。

采用数字控制的电流型逆变器电流环结构图如图3所示，角度误差与时间延迟共同串联于前向通道中构成控制延迟。交流侧开环传递函数由于滤波电容的存在呈现为高阶系统，存在谐振尖峰，需要采取适当阻尼策略加以抑制。

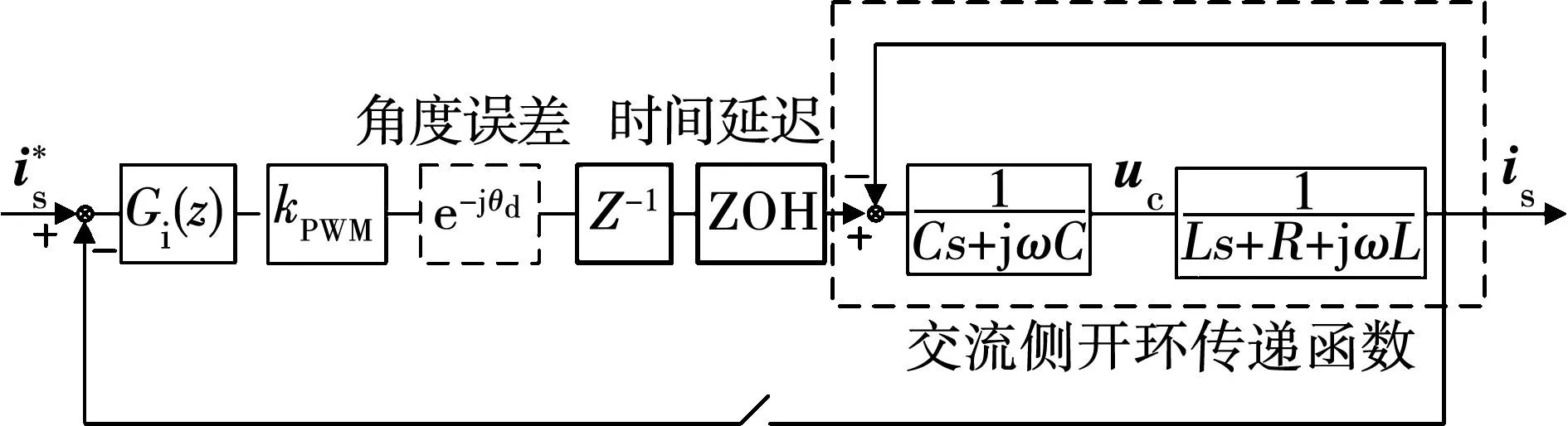
图3 数字控制电流型逆变器电流环结构图Fig.3 Structure diagram for current source inverter’s AC side when using digital control

2 反馈型有源阻尼

2.1 反馈型有源阻尼机理分析

电容电压反馈有源阻尼是电流型逆变器常用反馈阻尼方法，不考虑控制延迟时，其结构图如图4所示，其中反馈系数kR决定着阻尼效果。

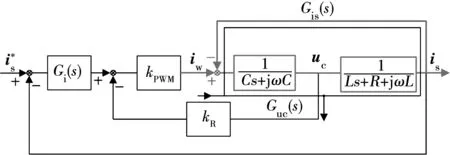
图4 电容电压反馈有源阻尼连续控制框图Fig.4 Structure diagram for active damping of capacitor voltage feedback type when using continuous control

分别写出逆变器输出电流iw到定子电流is和电容电压uc的复系数传递函数Gis(s)和Guc(s)，即：

(4)

其中Gis(s)即为交流侧开环传递函数。

根据式(4)将电流环控制框图变化为图5双闭环形式，电容电压反馈有源阻尼等效于电流环内一比例控制电压环，分别绘制电压闭环、交流侧开环和电流环开环的Bode图如图6所示。

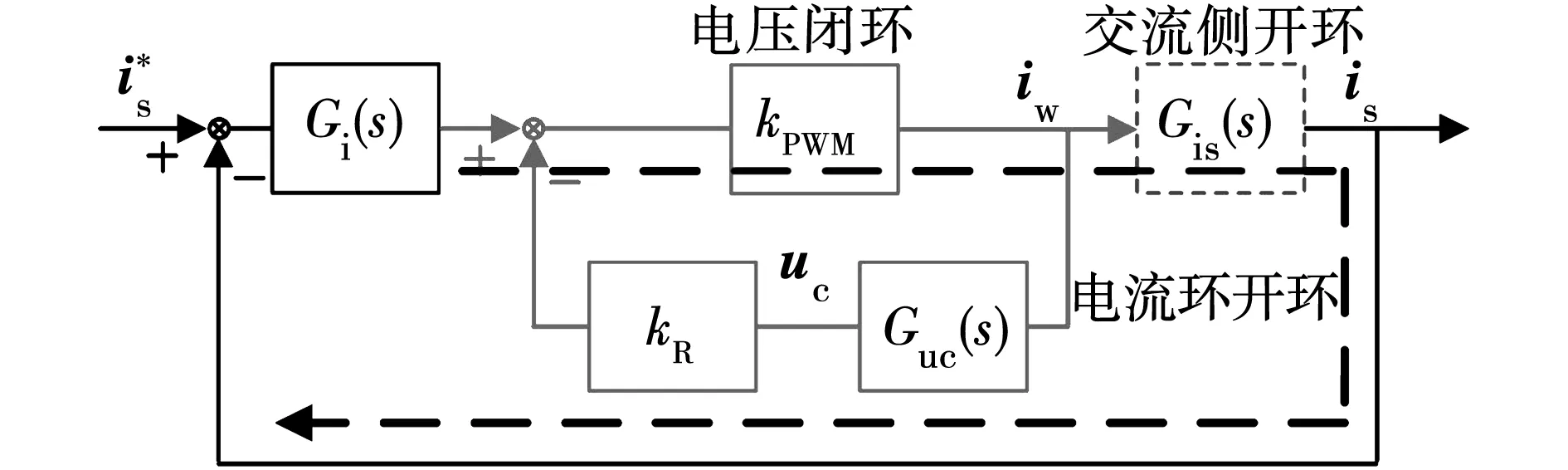
图5 电容电压反馈有源阻尼双闭环型结构图Fig.5 Double-closed-loop structure diagram for active damping of capacitor voltage feedback type

由图6可知，电容电压反馈等效于串联于前向通道中的陷波器，其在谐振频率处产生幅值衰减，抑制谐振尖峰。由闭环反馈控制原理可知，反馈系数越大，电压闭环在谐振频率处幅值降落越大，阻尼效果越好。与此同时，过大的反馈系数将导致截止频率增大，降低电压环稳定裕度。

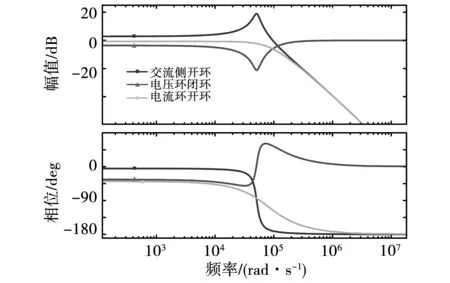
图6 电压反馈闭环、交流侧开环和电流环开环的Bode图Fig.6 Bode for closed loop of voltage feedback, open loop of AC side and current

2.2 控制延迟对电容电压反馈有源阻尼的影响

考虑控制延迟时，采用电容电压反馈有源阻尼的电流型逆变器控制框图，如图7(a)所示，同样可以根据式(4)将其变换为图7(b)双闭环形式，列写电压反馈环闭环传递函数为

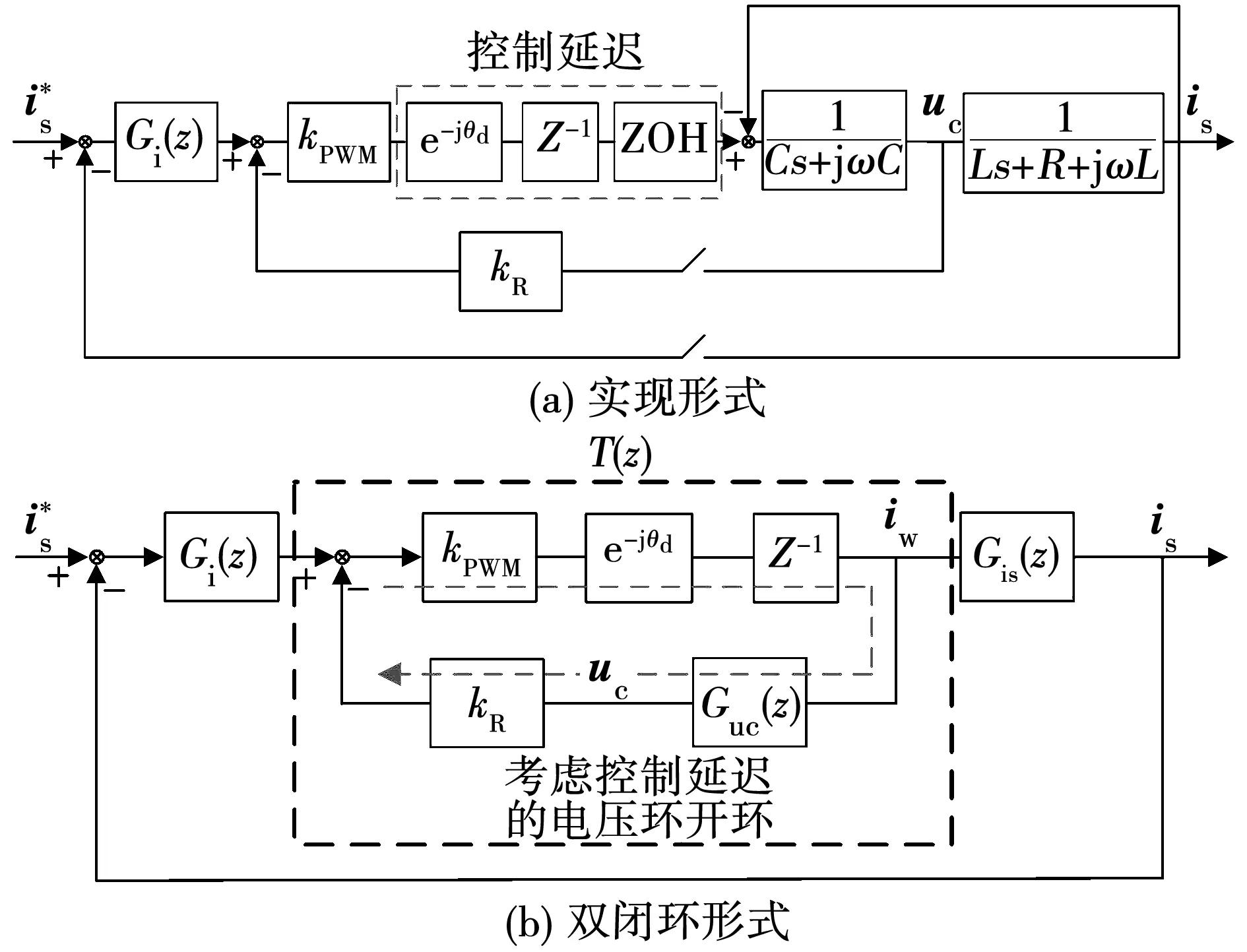
图7 数字控制电容电压反馈有源阻尼控制框图Fig.7 Structure diagram for active damping of capacitor voltage feedback type when using digital control

(5)

样机参数如第4节所示，由文献[15]可知，抑制谐振尖峰的充要条件为反馈系数kR小于等于0.4，此时，电压环闭环传递函数T(z)将含单位圆外极点。因此，电压反馈环无法在抑制谐振尖峰的前提下保证稳定。

控制延迟对电压反馈环开环Bode图的影响如图8所示，角度误差在全频段造成相位滞后，时间延迟引起的相位滞后随频率增加而增大。选取能够抑制谐振尖峰的反馈系数时，主要受时间延迟影响，截止频率将大于穿越频率，电压环不再满足稳定裕度的要求。

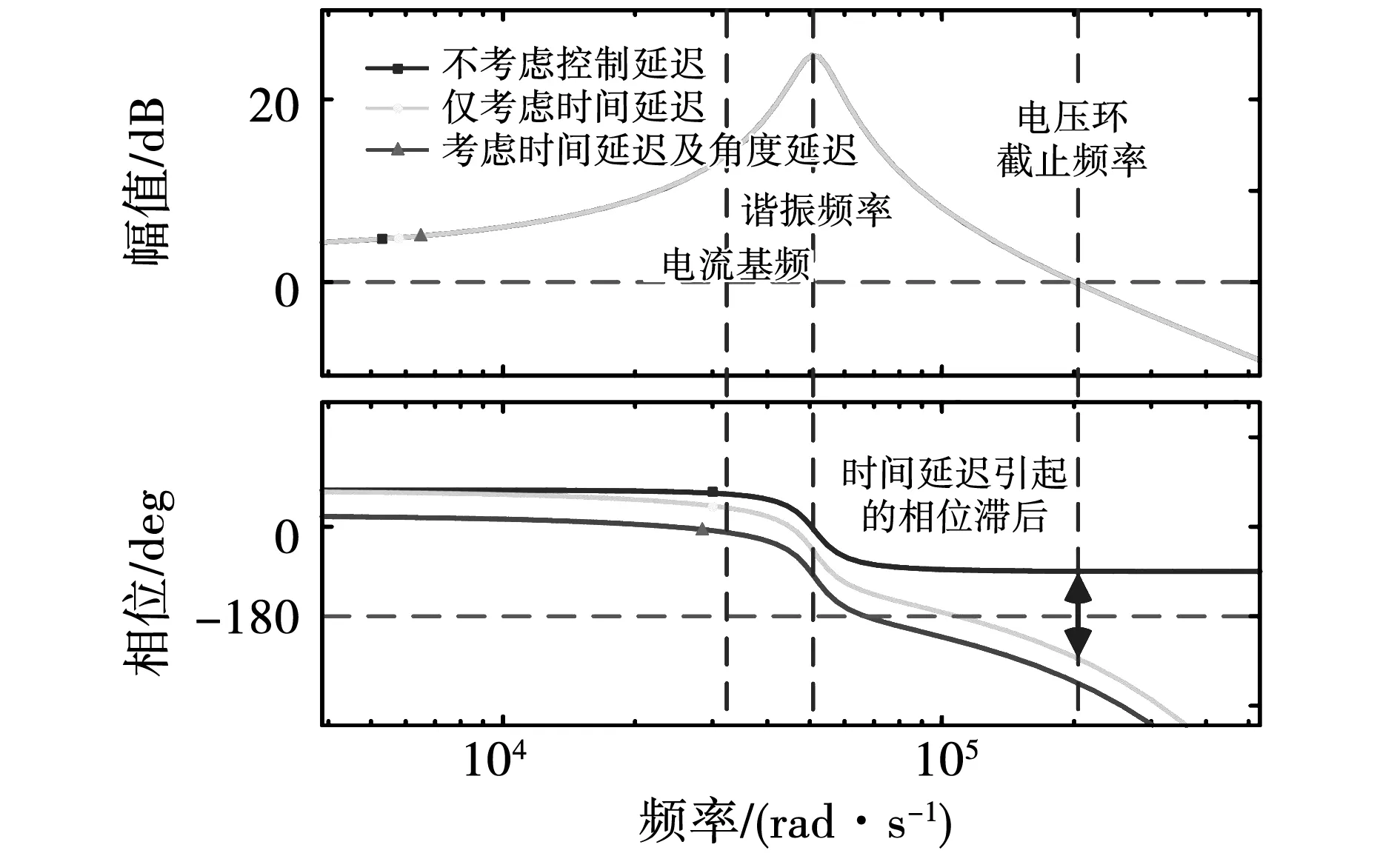
图8 控制延迟对电压环开环Bode图的影响Fig.8 Effect imposed on open loop Bode by control delay

为保证电流基频幅值不衰减，设计滤波电容时应确保谐振频率大于电流基频[16]，而电压反馈环截止频率总大于谐振频率，因此截止频率与额定电流频率正相关，截止频率处时间延迟引起的相位滞后大小也与额定电流频率正相关。在满足谐振抑制效果的前提下，对额定为550 kr/min的高速电机而言，电压环截止频率处时间延迟引起的相位滞后超过100°，传统不依赖模型的校正方法无法补偿时间延迟造成的电压环失稳。因此，电容电压反馈有源阻尼策略不适用于针对样机设计的电流型逆变器。

3 滤波型有源阻尼

3.1 带角度误差补偿的陷波器设计

通过在电流环前向通道中串联陷波器，可以改造其幅频特性，在拓展动态响应能力的同时避免电容压采样与引入电压反馈环导致的失稳。陷波器在连续域中的传递函数为

(6)

其中ωr为陷波频率，对应幅值降落称为陷波深度aωr，图9是陷波器Bode图，图中0.5aωr对应的频率之差称为陷波宽度2Δω，陷波深度及宽度与λ、ρ的关系为：

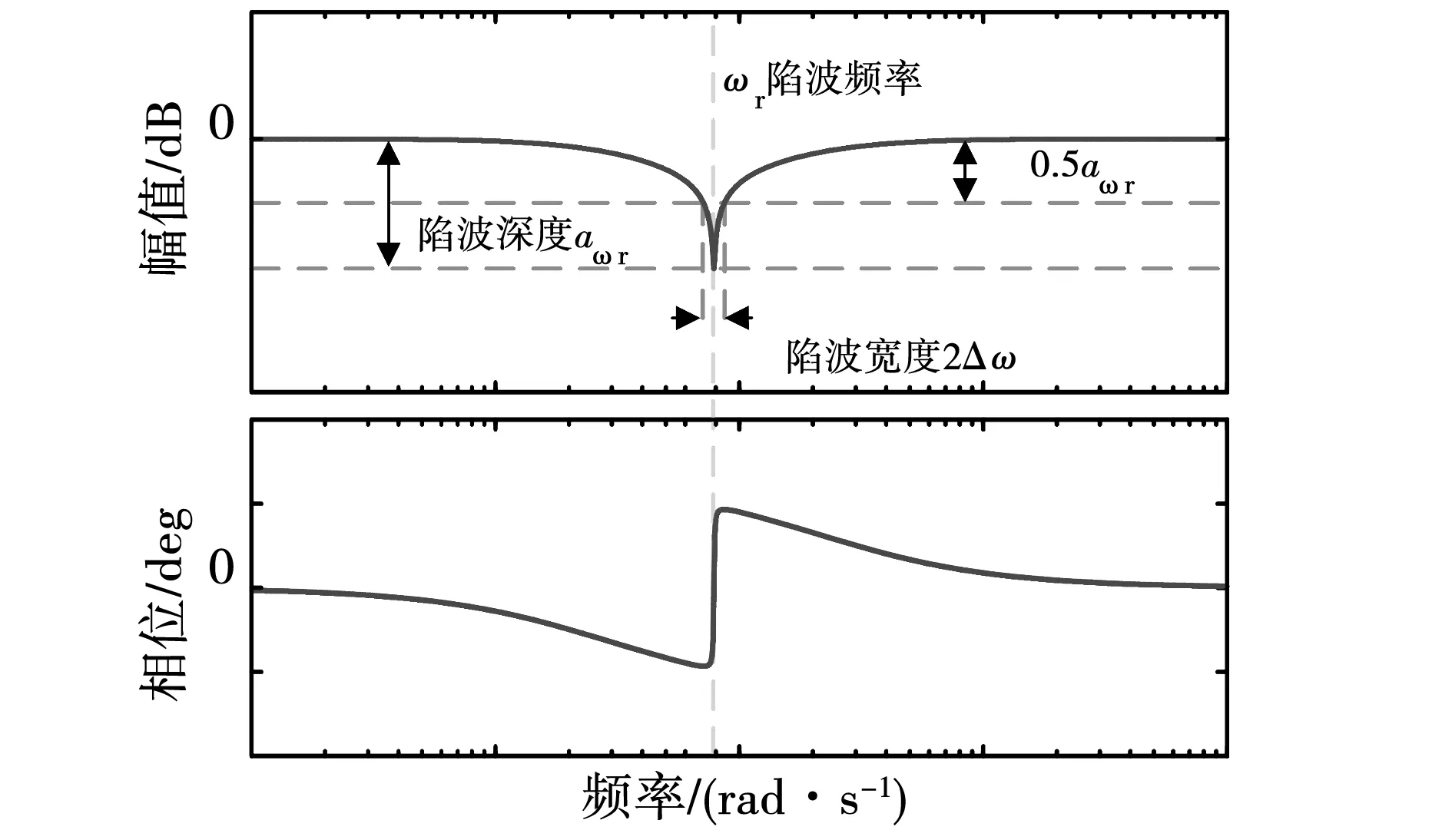
图9 陷波器Bode图Fig.9 Bode for notch

(7)

文献[17]对该结论进行了证明。

设定陷波器陷波频率等于谐振频率，在幅值降落0.5aωr时对消谐振尖峰，同时将陷波宽度设计为陷波频率ωr的十分之一，即2Δω=0.1ωr，以此加强陷波器在电机参数变化时的鲁棒性[17]。为保证陷波器在陷波频率处频率特性保持不变，采用预修正双线性变换对陷波器进行离散化，即

(8)

将式(8)代入式(6)即可得离散化后公式。

控制延迟对加入陷波器后的电流环开环Bode图的影响如图10所示。电流环截止频率小于谐振频率，由时间延迟引起的相位滞后造成的影响相较于反馈型有源阻尼大大减小，此时，影响系统稳定性能的主要是角度误差。如图11所示，在前向通道中加入角度误差补偿量即可提高系统稳定裕度。

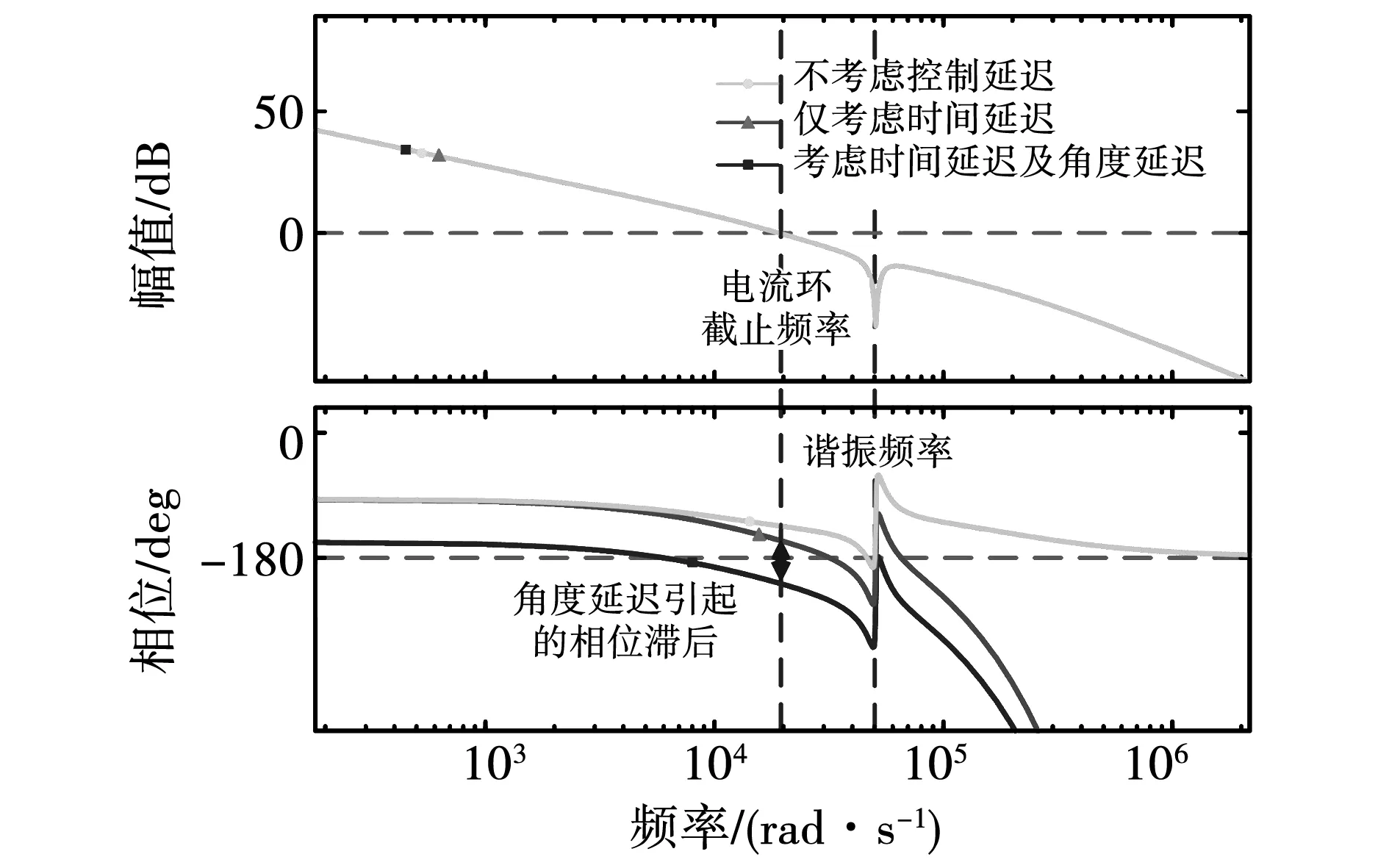
图10 控制延迟对加入陷波器的电流环Bode图的影响Fig.10 Effect imposed on current loop with notch by control delay

图11 带角度误差补偿的陷波器控制框图Fig.11 Structure diagram for notch with angle error compensation

3.2 陷波器阻尼方法全速域鲁棒性研究

式(1)所示电机耦合项在交流侧开环传函Gis(s)中引入了电机角速度，谐振频率不再只受电机参数影响，而随速度增大而减小，其变化趋势如图12所示。

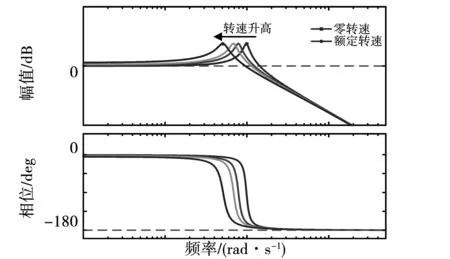
图12 谐振频率随转速变化Fig.12 Change of resonant frequency with speed variation

特定陷波器陷波频率固定，不同转速时交流测开环传函的谐振频率变化会影响阻尼效果，图13为根据额定转速(550 kr/min)及低速(100 r/min)设计的陷波器在额定转速时对谐振尖峰的抑制效果。加入陷波器后，谐振尖峰在一定程度上都受到了抑制，避免了电流环失稳，但相比于根据额定转速设计的陷波器，根据低转速设计的陷波器的幅值裕度大大下降，因此，不同转速对应谐振频率的变化会严重影响电流环的性能，在此基础上提出了陷波频率随转速变化的分段陷波器。

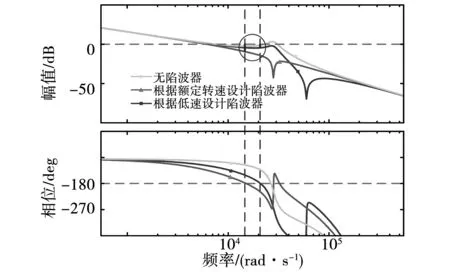
图13 根据不同转速设计的陷波器在额定转速的 阻尼效果Fig.13 Effect of damping when using different notch designed in different speed

开环传函Gis(s)的频率特性表达式为

G(jx)=

(9)

式中含有虚数j，其对应幅频特性表达式分母为两个根号项之和，通过求导计算谐振频率较为复杂。对其分析可以发现，电机电阻项起阻尼作用，对谐振频率影响较小。因此，构造无阻尼幅频特性和其取极值时对应频率(即为谐振频率)分别为：

(10)

(11)

式(11)所示谐振频率ωr与角速度ω呈正比，与图12中结论一致，将谐振频率代入陷波器传递函数Gnotch(s)，并在保持其它参数不变的前提下离散化，即可实现自适应陷波。为减少数字控制器计算负担，全速域以50 kr/min为一段划分，进行分段陷波控制，根据速域中点进行陷波器设计，以增强系统鲁棒性。各速域切换时，采用滞环切换方法以避免转速波动引起的震荡。

4 仿真与实验

4.1 仿真分析

为验证对高速低载频比下电流型逆变器有源阻尼策略的理论分析，在MATLAB/Simulink平台搭建仿真模型进行验证，电机参数与分析中一致，如表1所示，电机仅运行电流环，电流基频非特殊说明设定为额定值。

表1 高速永磁同步电机参数

图14为仅运行电容电压反馈环时d-q轴电容电压波形，在采样完成后即时反馈即可实现电压内环无延迟控制。q轴电压在给定从1 V阶跃至2 V时能够快速跟随，由于电压内环为比例控制，d-q轴电压将存在静差。加入控制延迟且补偿角度误差后系统失稳，说明电容电压反馈内环受时间延迟无法维持稳定。

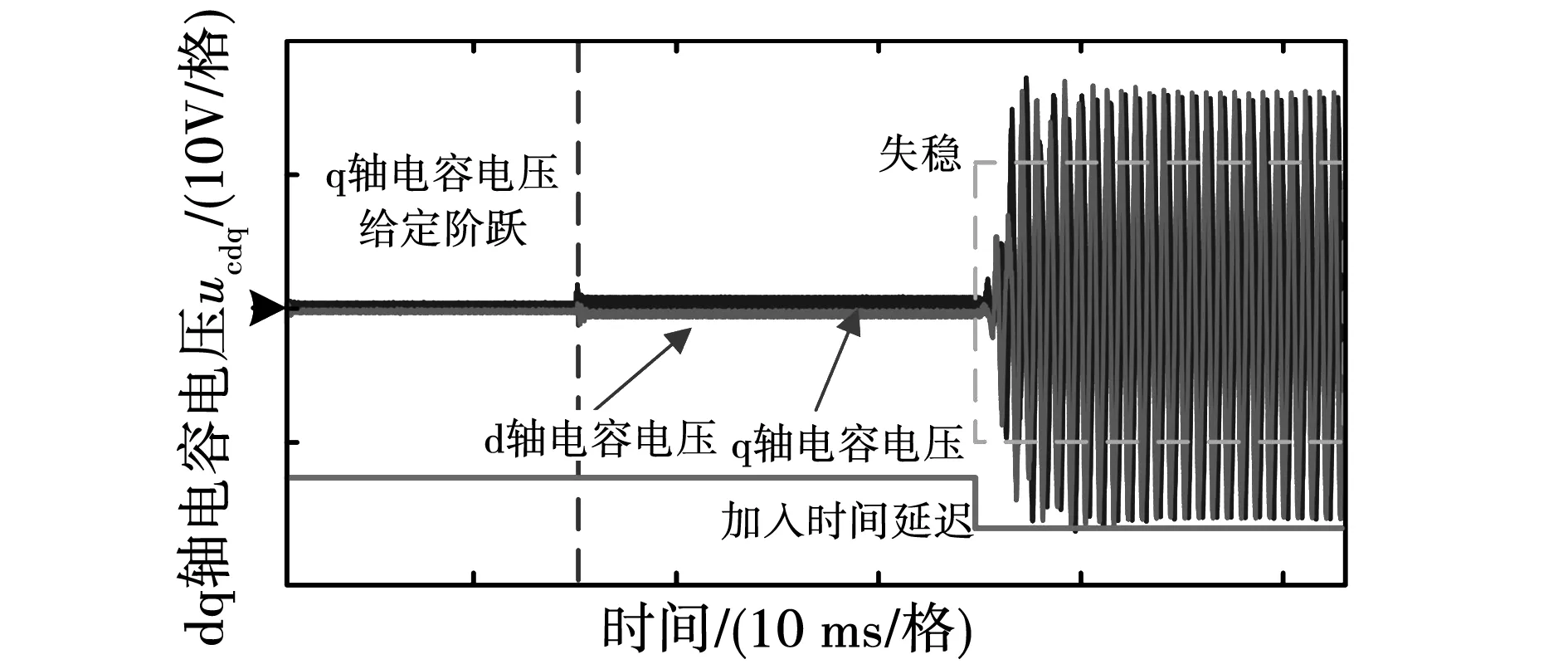
图14 电容电压反馈型有源阻尼dq轴电容电压Fig.14 d-q axis voltage when using active damping of capacitor voltage feedback type

陷波器串联在PI控制器之后，输入为期望逆变器电流量，陷波器滤除电流量如图15细节图所示，对其进行FFT频谱分析可知，该电流差值主要含谐振频率及开关频率附近分量，由此可知，数字陷波器能够实现滤除谐振频率附近分量的功能。旁路陷波器后，d-q轴电流逐渐失稳，重新加入陷波器后又能够恢复稳定，因此，陷波器能够提高系统稳定裕度，抑制谐振尖峰对稳定性的影响。

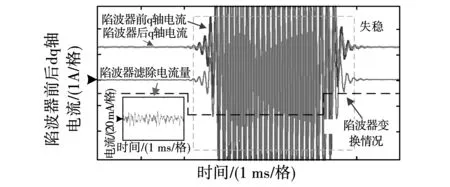
图15 陷波器对q轴电流的影响Fig.15 Effect of notch on q axis current

图8所示电容电压反馈内环中造成相位跌落的主要原因为时间延迟，电压环截止频率为20 100 rad/s时(kR=0.4,谐振尖峰得到抑制)，不同工作情况对应相位跌落如图16所示，即使在低速高控制频率时，由于截止频率过高，时间延迟造成的相位跌落仍然超过100°，对系统造成了难以补偿的影响；图10中造成电流环相位跌落的主要原因为角度误差，随着控制频率的下降及转速的升高，该相位跌落将如图17所示逐渐增大。控制频率选为100 kHz，角度误差在电流频率为8 050 Hz(且kp=0.27，ki=70)时造成了43.5°的相位跌落，此时电流环不再能维持稳定，三相电流如图18所示失稳。在前向通道中串联角度误差补偿后，电流环中角度误差造成的相位跌落消失，系统能够在额定工作点跟随给定。在不同电流基频采用了不同陷波器，其陷波中心频率随基频升高减小，基频升高过程中电流稳定，陷波器平滑切换。

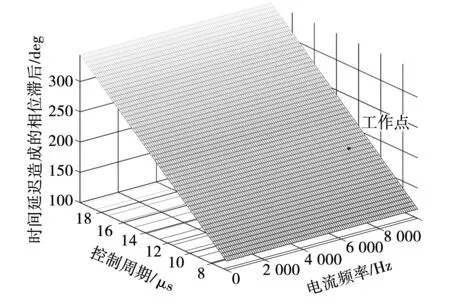
图16 采用反馈型有源阻尼时时间延迟对应相角 裕度降落Fig.16 Effect on phase margin imposed by time delay when using active damping of capacitor voltage feedback type

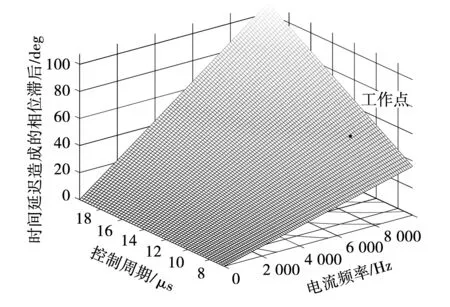
图17 采用滤波型有源阻尼时角度误差对应相角 裕度降落Fig.17 Effect on phase margin imposed by angle error when using active damping of filter type

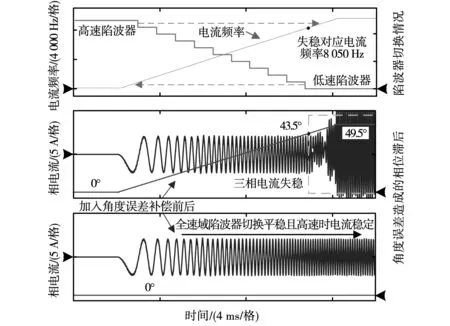
图18 角度误差补偿前后相电流随电流基频变换Fig.18 Change of current with frequency before and after compensating angle error

4.2 实验验证

为进一步验证理论研究及仿真结果，搭建如图19所示实验平台。功率器件选用安森美半导体公司的NVMFD6H852NL，主控芯片采用TI公司的TMS320F28377D且控制频率选为100 kHz，被测电机参数同表1且仅工作于电流环。

图19 电机及驱动平台Fig.19 Motor and driver

实验中数字控制器无法实现电流环即时运算，为验证控制延迟会导致电压反馈环失稳的结论，将电流环截止频率取为较小值(kp=0.1，ki=30)，此时谐振尖峰不再影响系统性能，电流环稳定裕度大。加入电压反馈且反馈系数与仿真中一致，相电流与电容电压立即失稳如图20所示，反馈型有源阻尼引入了失稳的电压反馈内环，电流环出现了单位圆外极点，与分析中一致。由于电压反馈环的失稳只与反馈系数有关，反馈型有源阻尼不适合针对样机设计的电流型逆变器。

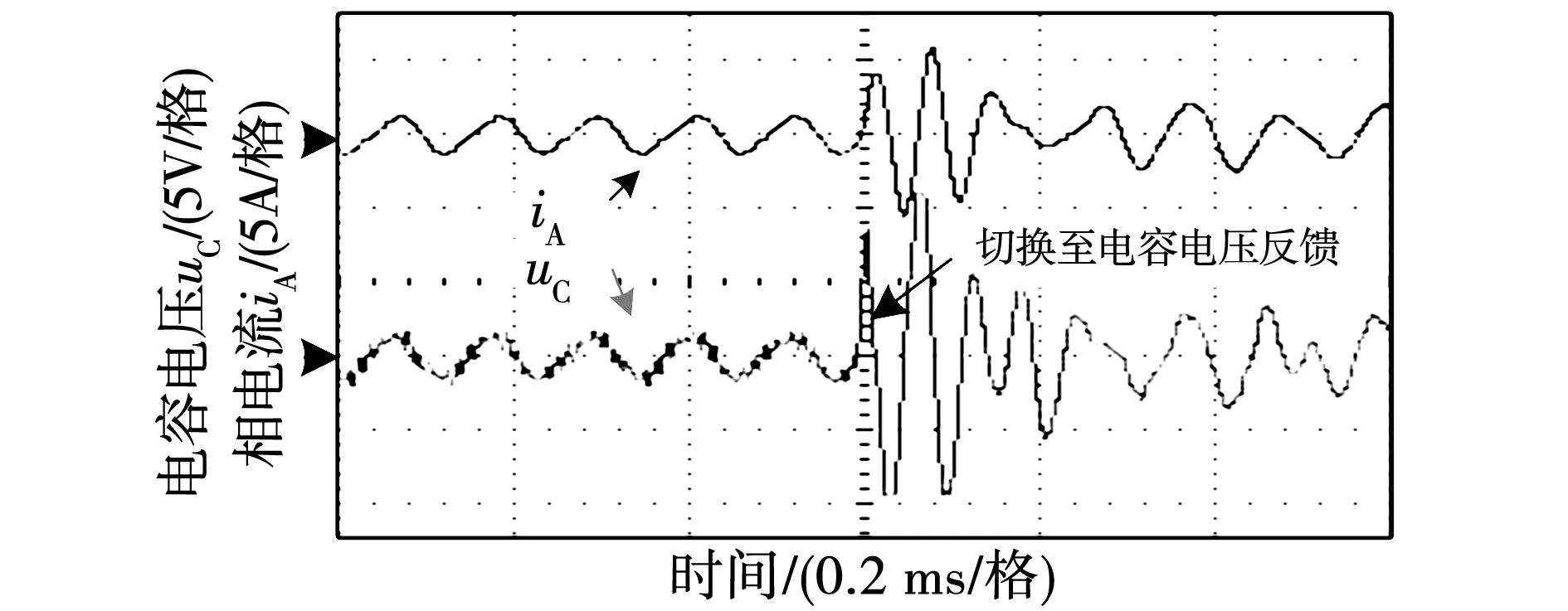
图20 电容电压反馈型有源阻尼相电流与电容电压Fig.20 Phase current and capacitor voltage when using active damping of capacitor voltage feedback type

陷波器对电流环影响如图21所示，去除陷波器后电流环失稳，重新加入后能恢复稳定，因此，数字陷波器能够有效抑制谐振尖峰，提高系统稳定性能。角度误差补偿对电流环影响如图22所示，随着电流频率增大，未加角度误差补偿的三相电流在6 900 Hz(413 kr/min)时失稳，而加入角度误差补偿的电流环在额定9 170 Hz(550 kr/min)仍能稳定运行，说明角度误差补偿在高速时能够有效补偿控制延迟引起的相位滞后，实验结果与图18仿真结果一致，证明了提出的带角度误差补偿的陷波器的有效性。

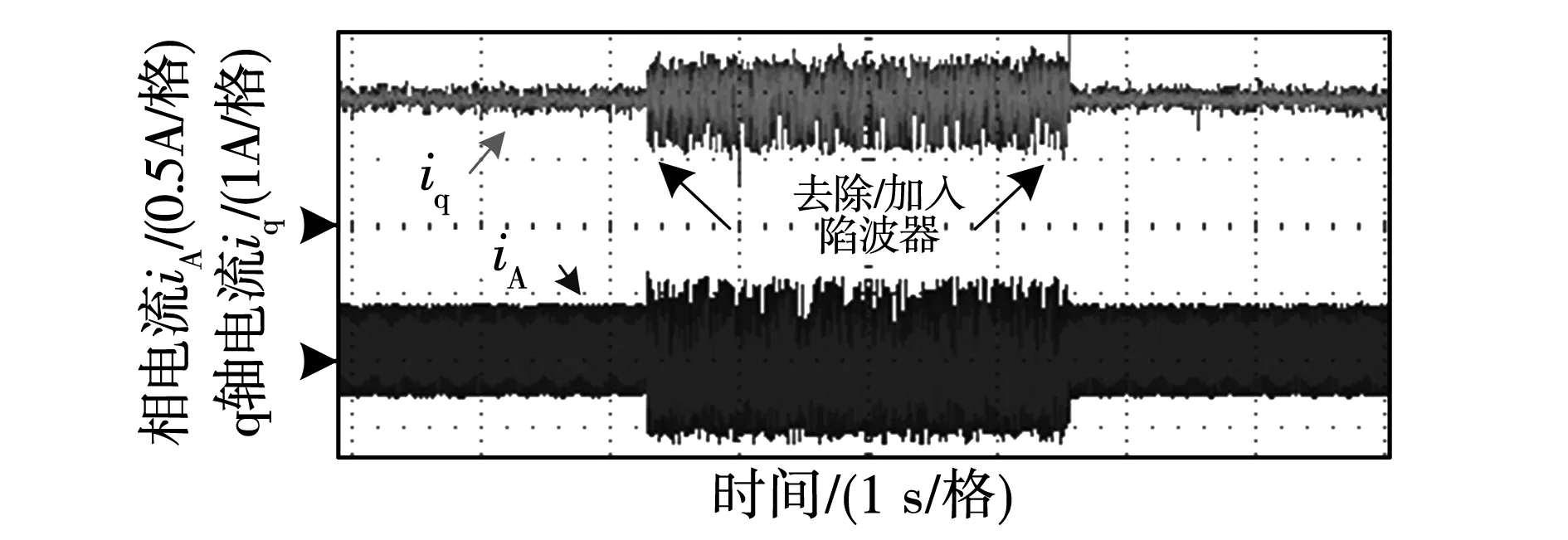
图21 加入/去除陷波器前后q轴与相电流Fig.21 q axis current and phase current before and after adding notch

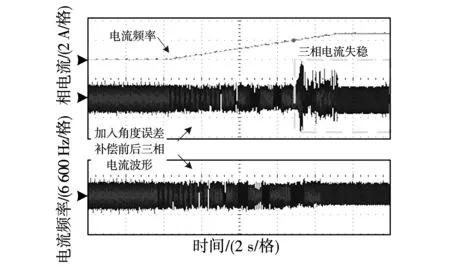
图22 角度误差补偿前后相电流随电流基频变换Fig.22 Change of current with frequency before and after compensating angle error

为说明根据不同转速设计的陷波器对额定基频下电流环的影响，在额定基频时将低速(100 r/min)陷波器切换至高速(550 kr/min)陷波器，q轴电流稳定性如图23所示明显提高，对应相电流波动减小，验证了谐振频率随转速的变化将影响电流环稳定裕度的结论。图24为相临速域陷波器切换时的相电流波形，由于两个陷波器在切换前同步运行，能够实现陷波器平滑切换，设计的分段陷波器能够满足全速域鲁棒控制的要求，实现如图22所示的全速域稳定运行。

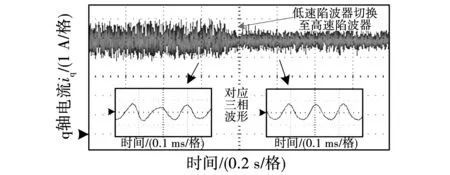
图23 根据不同转速设计的陷波器在额定基频时 阻尼效果Fig.23 Effect of damping when using notch designed in different speed

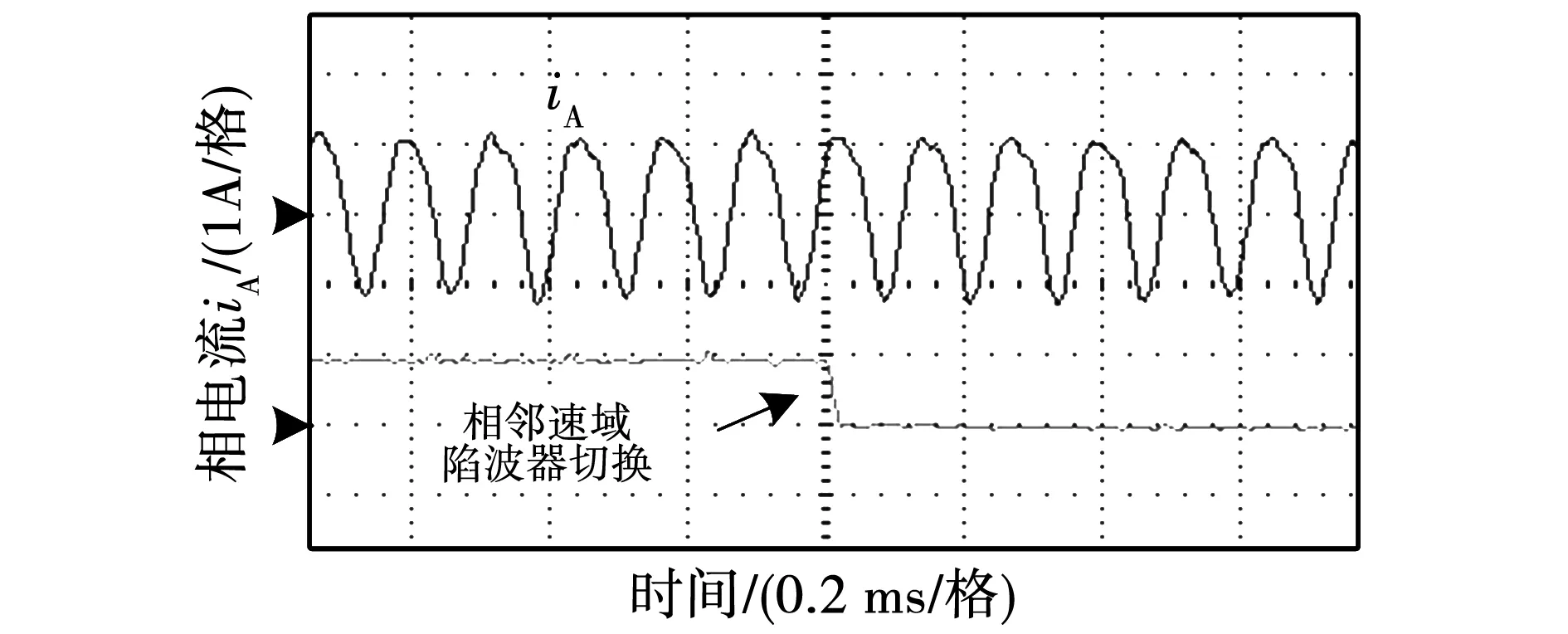
图24 相临速域陷波器切换时相电流波形Fig.24 Phase current when neighbouring notch changes

5 结 论

本文首先使用复矢量对电流型逆变器进行了建模，并对比了反馈型及陷波器型两种有源阻尼策略。其后分析了数字控制延迟造成严重相位滞后的原理，得出了采用反馈型有源阻尼将存在单位圆外极点的结论。为实现电流环在额定频率的稳定运行，本文提出了带角度误差补偿的陷波器，并通过分段陷波的方法实现了全速域鲁棒控制。最后，本文通过仿真及实验验证了高速低载频比下对电流型逆变器有源阻尼策略的研究。