不同通风结构下高铁异步牵引电机温度场分析

曹君慈， 闫华， 李栋， 王宇， 李伟力

(北京交通大学 电气工程学院，北京 100044)

0 引 言

随着高速铁路的不断发展，列车对牵引性能的要求逐渐提高，牵引电机向着高效率、高功率密度发展[1]。异步电机具有结构简单、维护量小等优势，在动车组牵引电机中得到普遍应用。近年来我国高速动车组异步牵引电机运行中出现了较多的热问题，这些热问题多是由于电机通风不畅而导致的温升过高。因此，计算电机温升、优化电机通风结构、降低电机温度是亟待解决的关键性问题。

电机温升计算方法有简化公式法、热网络法和数值计算方法[2-4]，其中数值计算方法又包括有限元法、有限差分法、有限体积法等。简化公式法模型简单但准确性较低。热网络法类比电路模型构建网络，计算速度较快，文献[5-10]分别采用热网络法计算了不同种类电机温度场并通过实验验证了热网络法的准确性。数值计算方法中，有限差分法主要用于早期温度场计算[11]；有限元法对计算机要求较高，适合处理复杂区域[12]；有限体积法对网格的适应性很好，近几年来被广泛应用。文献[13-17]分别采用有限体积法计算了不同功率的永磁同步电机温度场，分析了不同因素对电机温升的影响规律，并开展了温升实验验证。文献[18-20]分别采用有限体积法计算了立式鼠笼异步电动机、全轴向通风无刷励磁机和变压器绕组的温升。近几年，有部分学者利用新颖的神经网络等算法预测了电机的温度分布[21-22]，为电机温度场研究开拓了新的方向，但热网络法和有限体积法仍是目前电机温度场计算的主流方法。文献[23]分别利用热网络法和有限体积法计算了330 MW汽轮发电机一齿一槽区域的三维温度场，两种方法计算的绕组最大温度仅相差3.7 ℃，热网络法计算时间为5 s，而有限体积法计算时间为3 h，可见热网络法计算更加快捷，但与实验数据相比，有限体积法的误差更小，计算精度更高。

本文采用有限体积法对一台600 kW异步牵引电机进行数值分析，在原始通风结构的基础上研究了通风孔孔径对电机温度场的影响规律，结合电机定子槽数提出了正对电机定子槽的通风结构，并研究了该结构对电机散热的影响。此外，本文提出两段截面的定转子通风结构，大幅降低电机最高温度，平衡了电机轴向温差，为风冷异步牵引电机的冷却流道研究提供一定的意义。

1 电机模型

1.1 电机参数

本文所述电机为600 kW高速列车用异步牵引电机，采用无外壳结构，轴向分别开定子和转子通风孔，采用强迫风冷的散热方式，绝缘等级200级，基本参数如表1所示。

根据电机参数建立的电机三维全域仿真模型如图1所示，电机采用径向入风、轴向出风的通风方式，冷却空气经入风口流入后，分别经过定子通风孔、转子通风孔和气隙流到出风口，其中定子通风孔和转子通风孔均为圆柱形结构，定子通风孔为36个、孔径22 mm，转子通风孔16个、孔径24 mm。

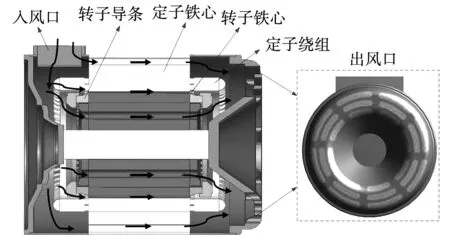
图1 异步牵引电机结构示意图Fig.1 Structure of asynchronous traction motor

1.2 数学模型

本文对电机额定状态下的稳态温度场进行计算，热量传递不考虑热辐射，主要以热对流和热传导的形式发生。在笛卡尔坐标系下，异步牵引电机各向异性介质的三维热传导方程如下式所示，导热方程中不含时间项，但含有热源[24]：

(1)

式中：T为待求温度；kx、ky、kz分别是x、y、z方向的导热系数；qv为热源密度；S1为绝热面；S2为散热面；α为散热表面的散热系数；Tf为周围流体的温度。

所有的流动传热过程都受物理规律制约，基本的守恒规律包括：质量守恒规律、动量守恒规律和能量守恒规律，各基本控制方程的通用形式[25]为

(2)

式中：Φ为通用变量；ρ为流体密度，kg/m3；υ为速度矢量；Γ为广义扩散系数；s为源项。

此外，该电机流体区域的雷诺数远大于2 300，因此电机内流体状态属于湍流。本文采用Realizablek-ε湍流模型进行数值模拟，其湍流动能和耗散率的输运方程[13]为：

(3)

式中：k为湍流动能；ε为扩散因子；ρ为流体密度；t为时间；Gk表示由于平均速度梯度产生的湍流动能；Gb表示由于浮力影响产生的湍流动能；YM表示可压速湍流脉动膨胀对总的耗散率的影响；C2和C1ε是常数，σk、σε分别是湍流动能及其耗散率的普朗特数,C1ε=1.44、C2=1.9、σk=1.0、σε=1.2。

1.3 基本假设

为合理简化流固耦合模型的求解计算过程，做出基本假设如下[26-27]：

1)由于电机采用强迫通风方式，在标准大气压下流体浮力和重力对电机内流体流动影响很小，故对其忽略不计；

2)电机内流体流动速度小于声速，流体作为不可压缩流体处理；

3)绕组绝缘浸漆均匀；

4)认定槽楔与绝缘同宽，具有相同的绝缘属性；

5)假定热源密度在电机各部件中均匀分布。

1.4 边界条件

根据电机额定状态的运行性能及计算域的特点，列出边界条件如下：

1)入口边界定义为速度入口：25.5 m/s；

2)出口边界定义为压力出口：初始压力为1个大气压；

3)与空气接触的固体表面均为无滑移边界条件。

1.5 热生成率计算

电机的各部件损耗是计算温度场的热源，但有限体积法进行热分析所需热源为体热源，即需要把电机各部分损耗转换为单位体积的热生成率，电机各部分热生成率如表2所示。

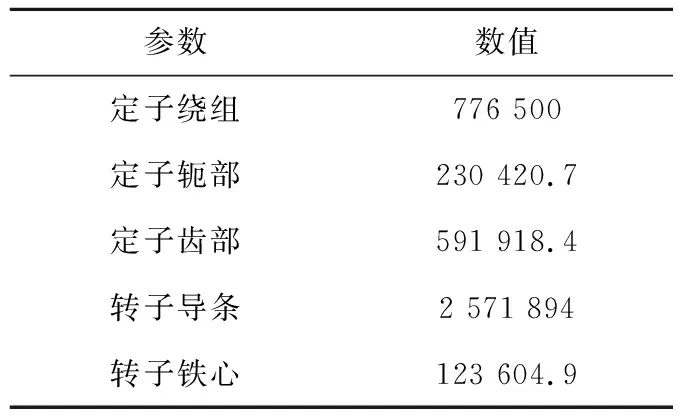
表2 异步牵引电机热生成率

1.6 网格划分

有限体积法计算电机温度场和流体场需要把空间上连续计算区域内的控制方程进行离散，这就需要对模型进行网格划分，网格质量对计算收敛度及结果的准确性具有很大影响。本文采用多面体网格对模型进行网格划分，与四面体网格相比，相同条件下多面体网格数量更少，计算精度较高，且与相邻网格之间的连接性较好，可以极大地提高计算收敛性，网格划分结果如图2所示，该网格数量为6 894 121，网格整体质量较好，计算收敛较快。

图2 网格划分结果Fig.2 Meshing results

2 原始通风模型分析

2.1 原始模型温度场和流体场分析

利用有限体积法对原始通风模型进行仿真，得到流体迹线图如图3所示，可以看到，空气经进风口流入后，径直流入进风口侧机腔，且在两侧形成环流，而后分别通过定子通风孔、转子通风孔和气隙流到出风口侧机腔，在定转子通风孔出口处也形成了环流，最后经出风口流出。

图3 原始通风模型流体迹线图Fig.3 Streamline of the original ventilation model

原始模型的温度分布如图4所示，可以看到，电机各部分温度分布趋势一致，均是入风口侧温度较低，出风口侧温度较高，其中电机整体最高温度为248.57 ℃，位于靠近出风口侧的转子导条端部。

图4 原始通风模型温度分布Fig.4 Temperature distribution of original ventilation model

2.2 原始模型实验验证

为验证仿真结果的正确性，利用图5所示的实验平台进行测试实验。温升实验测得额定状况下图6所示A点的温度，即靠近定子槽底的铁心轭部位置，其温升为110.6 ℃，而A点的仿真温度为130 ℃，其中环境温度为16 ℃，温升为114 ℃，仿真温度与实测温度的误差约为3%。此外，实验还测取了进风口的压力：静压1 906 Pa，动压727 Pa；而仿真得到的进风口静压和动压分别为1 807 Pa和694 Pa，误差分别为5.2%和4.5%。实验数据与仿真数据的对比结果误差较小，符合工程要求，证明了仿真结果的正确性。

图5 实验测试平台Fig.5 Test bench for experiments

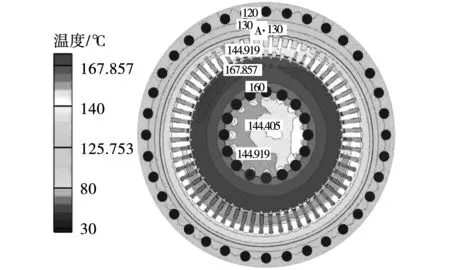
图6 原始通风模型径向截面温度分布Fig.6 Radial section temperature distribution of the original ventilation model

3 不同定子通风结构对电机温度场的影响

3.1 通风孔孔径对电机温度场的影响

为探究通风孔孔径对电机温升的影响规律，改变原始通风模型定子通风孔的孔径，方案如表3所示。

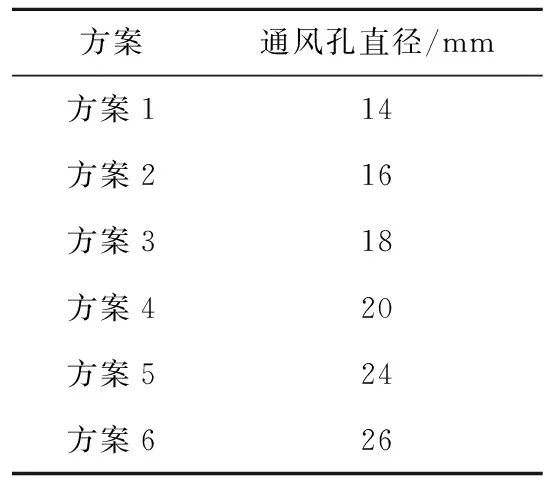
表3 通风孔孔径变化方案

对具有不同通风孔直径的电机模型进行仿真，迭代计算收敛后，得到电机各部分最大温度如图7所示。可以看出，随着通风孔截面直径的增大，电机各部分温度变大。转子绕组和转子铁心的温度呈线性增大趋势，而定子部分从方案3到方案6温度增加较为明显，当通风孔截面直径小于方案3所设计的18 mm时，定子部分温度变化较为平缓。

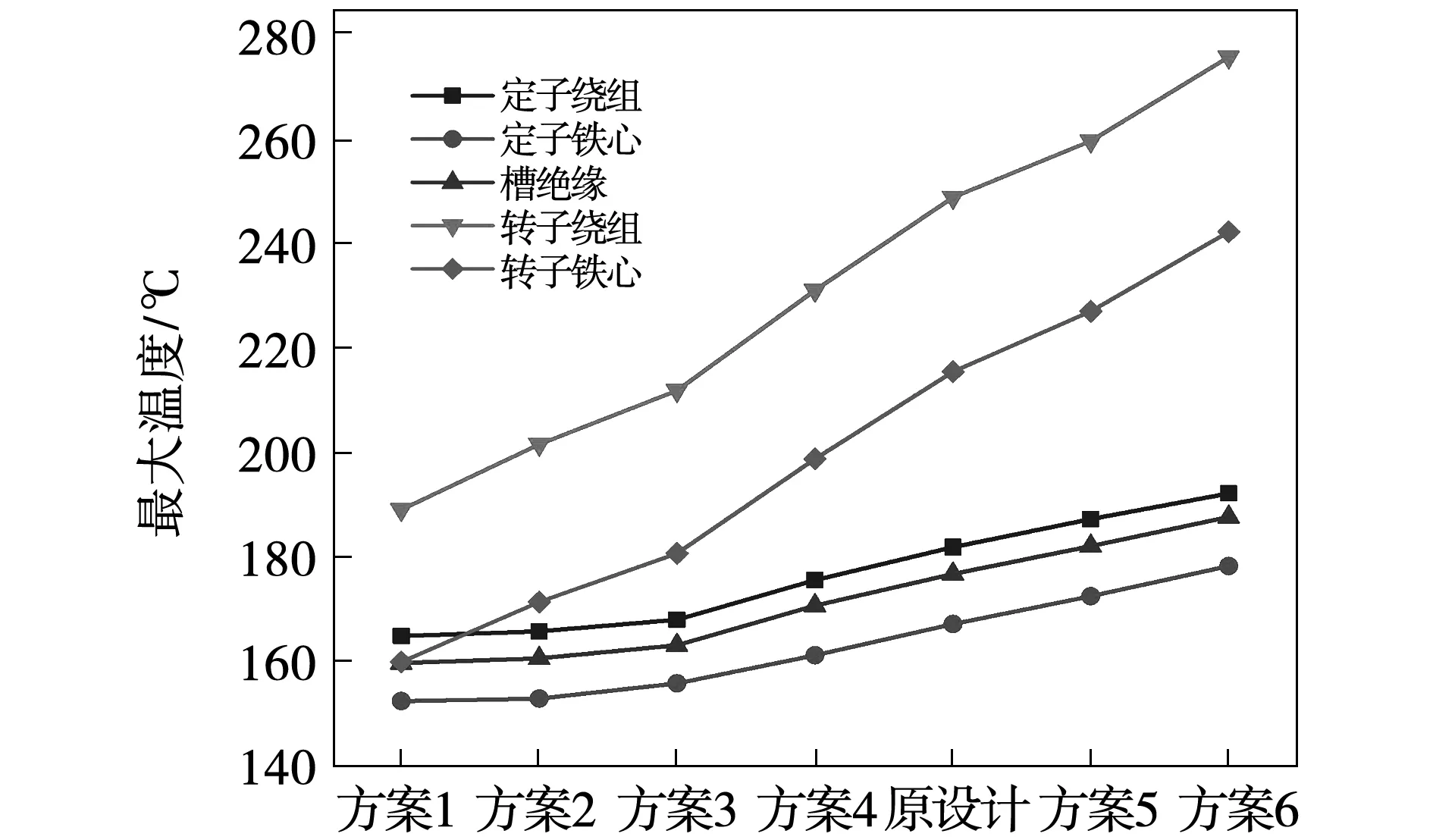
图7 孔径不同时各方案温度对比Fig.7 Temperature comparison of schemes with different diameter

图8给出了通风孔截面直径变化时，各方案定子通风孔和转子通风孔内的轴向风速变化图，其中横轴轴向位置指从入风口侧到出风口侧。冷却风从入风口流入后，以较大的压力流向定子和转子通风孔，导致轴向起始位置风速较大，但进入定子和转子通风孔后，风速几乎不再变化。

康川司法所接收的社区服刑人员一般为被判处缓刑的人员。在缓刑期内，如果服刑人员遵守法律规定并遵守社区矫正的工作规定，在缓刑期满30日前，社区服刑人员写出个人总结上交司法所。矫正期满时，司法所根据服刑人员的实际表现填写鉴定矫正期满表并公开宣告解除社区矫正。湟中县司法局向社区服刑人员发出解除社区矫正的证明书，之后便将解除社区矫正的人员纳入安置帮教管理工作中。

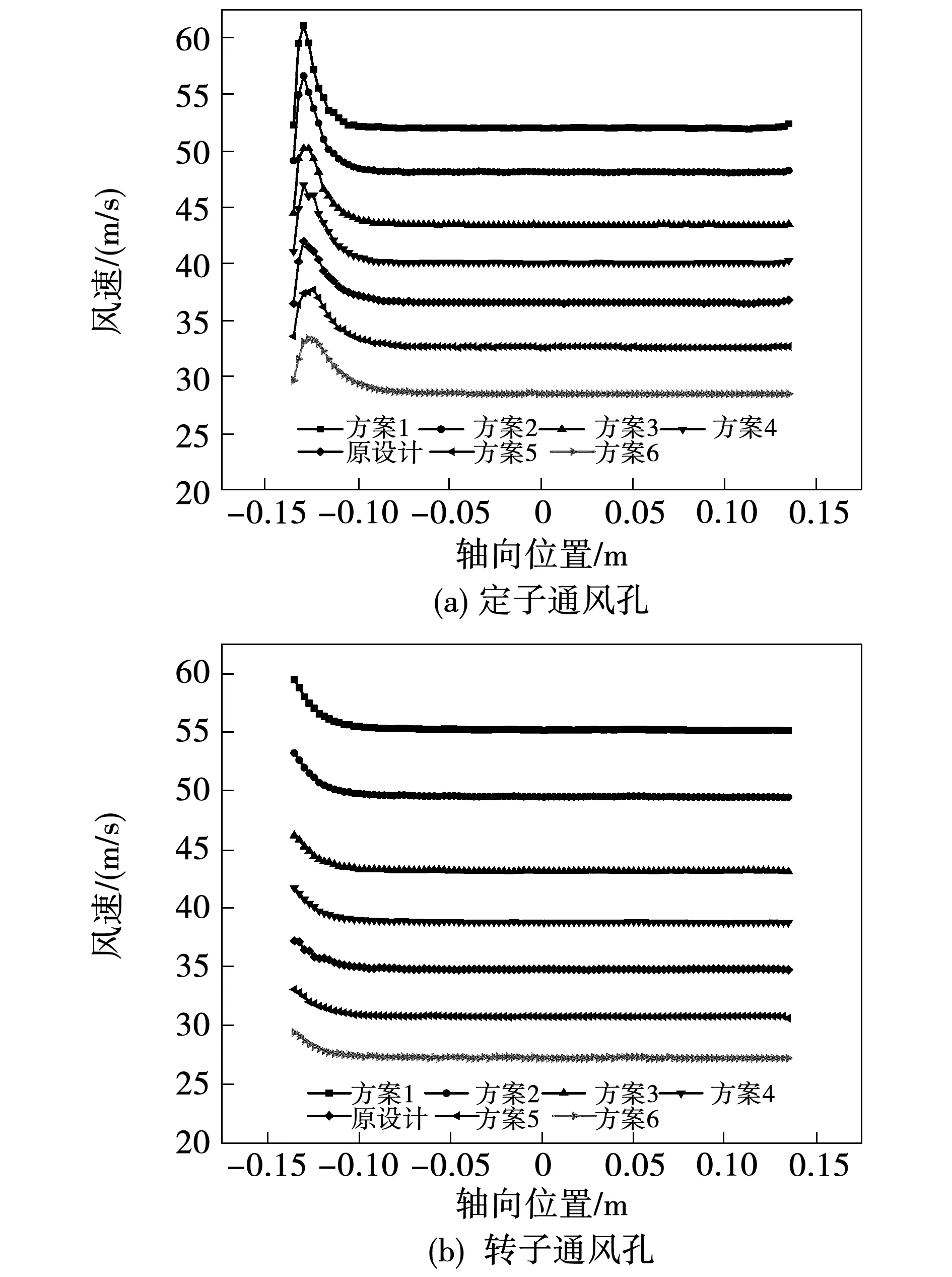
图8 孔径不同时各方案风速对比结果Fig.8 Velocity comparison of schemes with different diameter

从方案1到方案6，通风孔截面直径逐渐变大，定子通风孔和转子通风孔内风速下降明显，其中定子通风孔最大风速差约为24 m/s，而转子通风孔最大风速差约为28 m/s。

由温度和风速对比可知，通风孔截面直径对电机温度影响显著，截面直径越大，通风孔内风速越小，带走热量的能力越弱，从而电机各部分温度越高。但图7所示的转子部分温度变化比定子部分温度变化更显著，为了探究这一现象，分别提取不同孔径方案下定子和转子通风孔的入口流量进行分析，对比结果如图9所示。可以看出，从方案1到方案6，即随着孔径的增大，定子通风孔内流量持续上升，这对定子部分的温度上升起抑制作用；而转子通风孔内流量持续下降，进一步促进了转子部分的温度增加；因此，定子通风孔孔径增大时，转子部分比定子部分温度变化更显著。

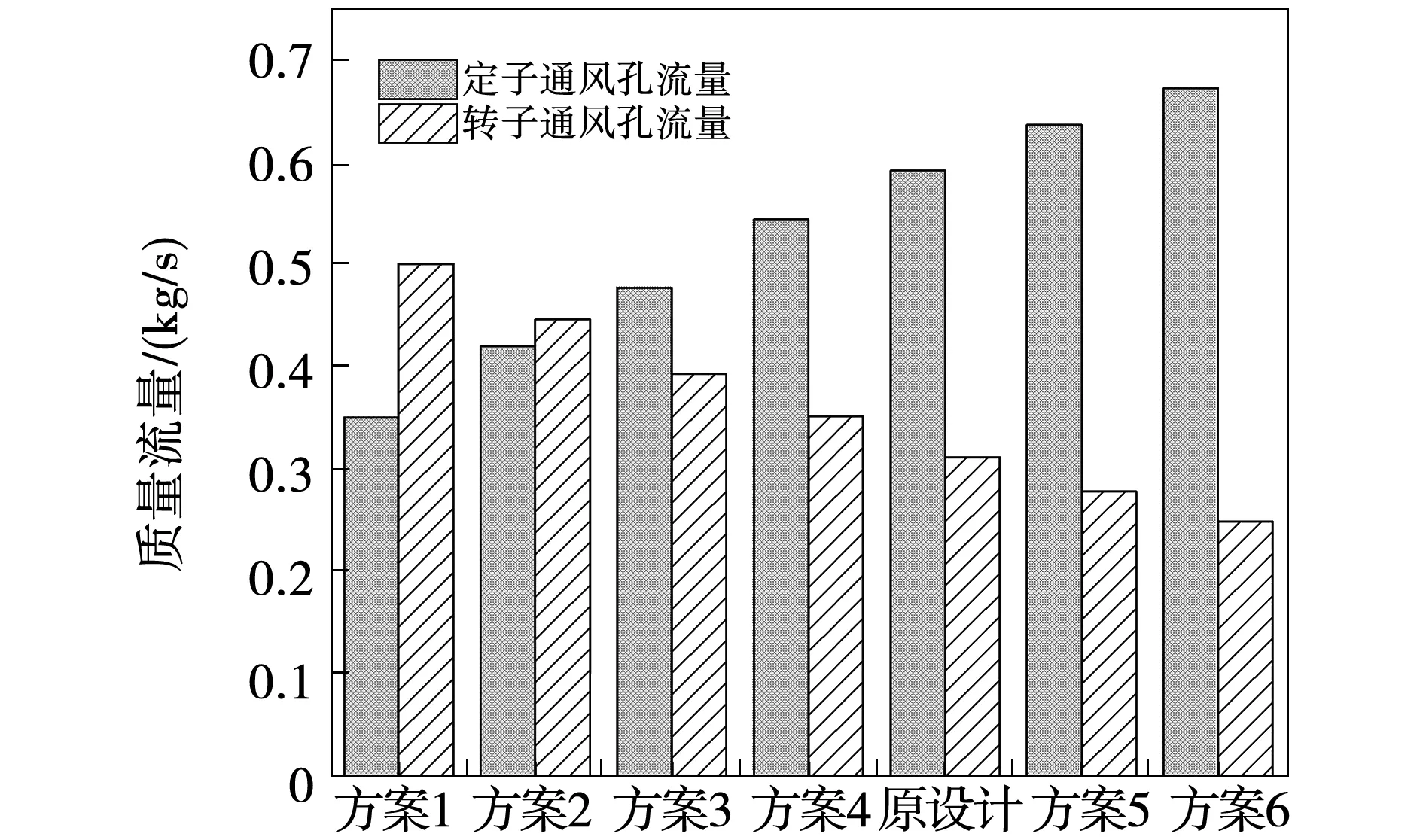
图9 孔径不同时通风孔流量对比结果Fig.9 Mass flow comparison of ventilation holes with different diameter

综上所述，当定子通风孔孔径变化时，电机温度变化同时受风速和通风孔流量的影响，但是风速影响作用更大，起决定性作用。

3.2 正对定子槽的通风孔对电机温度的影响

由于通风孔孔径减小时冷却效果明显，本节把原始模型中36个直径为22 mm的通风孔孔径减小，又因所述电机定子槽数为60，为了进一步研究定子通风孔对电机绕组的影响，本节在保证定子通风孔体积不变的前提下，将原始模型中36个22 mm的定子通风孔修改为60个正对定子槽的通风孔，对应孔径减小到17.04 mm，探究正对定子槽的通风结构对电机温度的影响规律，定子通风孔位置示意图如图10所示，定义该方案为方案7。

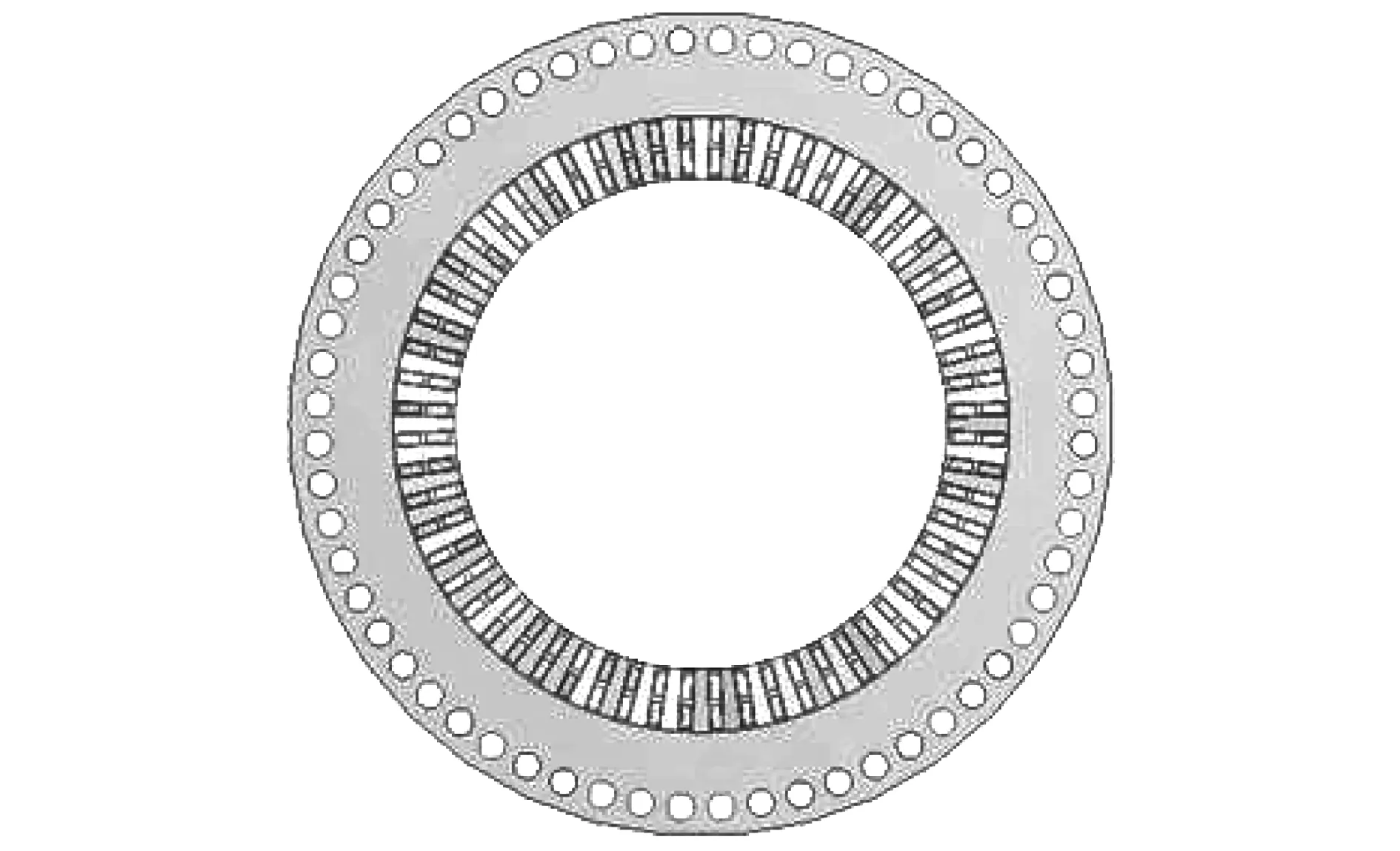
图10 方案7定子通风孔位置示意图Fig.10 Schematic diagram of stator ventilation holes location in scheme 7

图11为方案7模型的温度仿真结果，可以看出，电机温度从入风口侧到出风口侧逐渐增大，各部件最高温度均出现在出风口侧，这与原始模型的仿真结果相同，原因是入风口侧通风孔内风速较大且风温较低，有较强的能力带走热流量，但是随着轴向距离的增加，通风孔内风温逐渐增加，带走热量的能力减弱，导致出风口侧温度较高。该结构与原始模型相比，定子绕组部分温度均有所下降，其中定子绕组、定子铁心和绝缘最高温度分别减小6.2%、8.4%和7.6%，转子部分温度变化不明显，转子导条和转子铁心的最高温度变化不足2%。

图11 方案7温度分布Fig.11 Temperature distribution of scheme 7

图12为原始模型和方案7的定子通风孔和转子通风孔的壁面传热系数对比图，可以看到，传热系数最大值均位于入风口侧，方案7的定子通风孔传热系数最大值比原始模型提升15.8%，而转子通风孔仅提升7.9%。

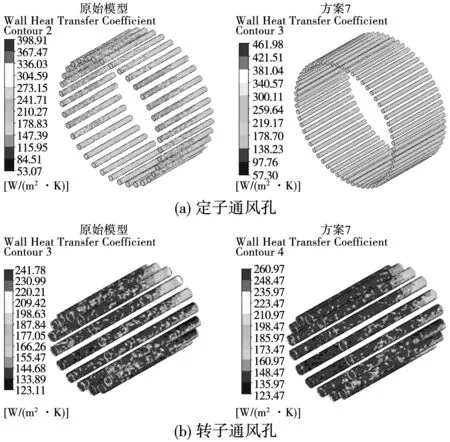
图12 定转子通风孔壁面传热系数对比结果Fig.12 Comparison of wall heat transfer coefficient of stator and rotor ventilation holes

两方案下定子通风孔和转子通风孔的平均壁面系数对比如表4所示，与原始模型相比，方案7的定子通风孔的平均传热系数增大8.944 W/(m2·K)，而转子通风孔平均壁面传热系数仅增大0.68 W/(m2·K)。由此可知，方案7在定子通风孔体积不变的情况下，孔径减小导致定子通风孔内风速增大，定子通风孔流量增多，平均壁面传热系数显著增大，散热能力提升，从而有效降低了定子部分的温度。

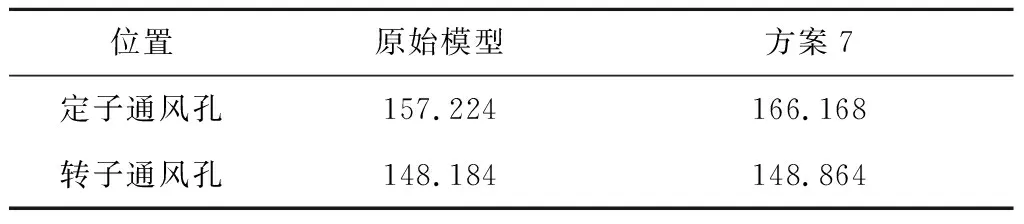
表4 定转子通风孔平均壁面系数对比结果

3.3 分段式通风孔对电机温度的影响

由上述研究可知，减小定子通风孔的孔径可有效降低定子绕组最高温升，但是通过电机的温度分布趋势可以看出，电机各部分轴向温度分布不均匀，出风口侧温度较高，存在轴向温差较大的问题。结合文献[28]提出的冷却流道结构形式，在3.2节所述的通风结构的基础上，把定转子通风孔出风口侧孔径减小为原始模型的一半，得到分段式定转子通风孔，结构示意图如图13所示，定义该模型为方案8。

图13 分段通风孔结构示意图Fig.13 Schematic diagram of segmented ventilation holes

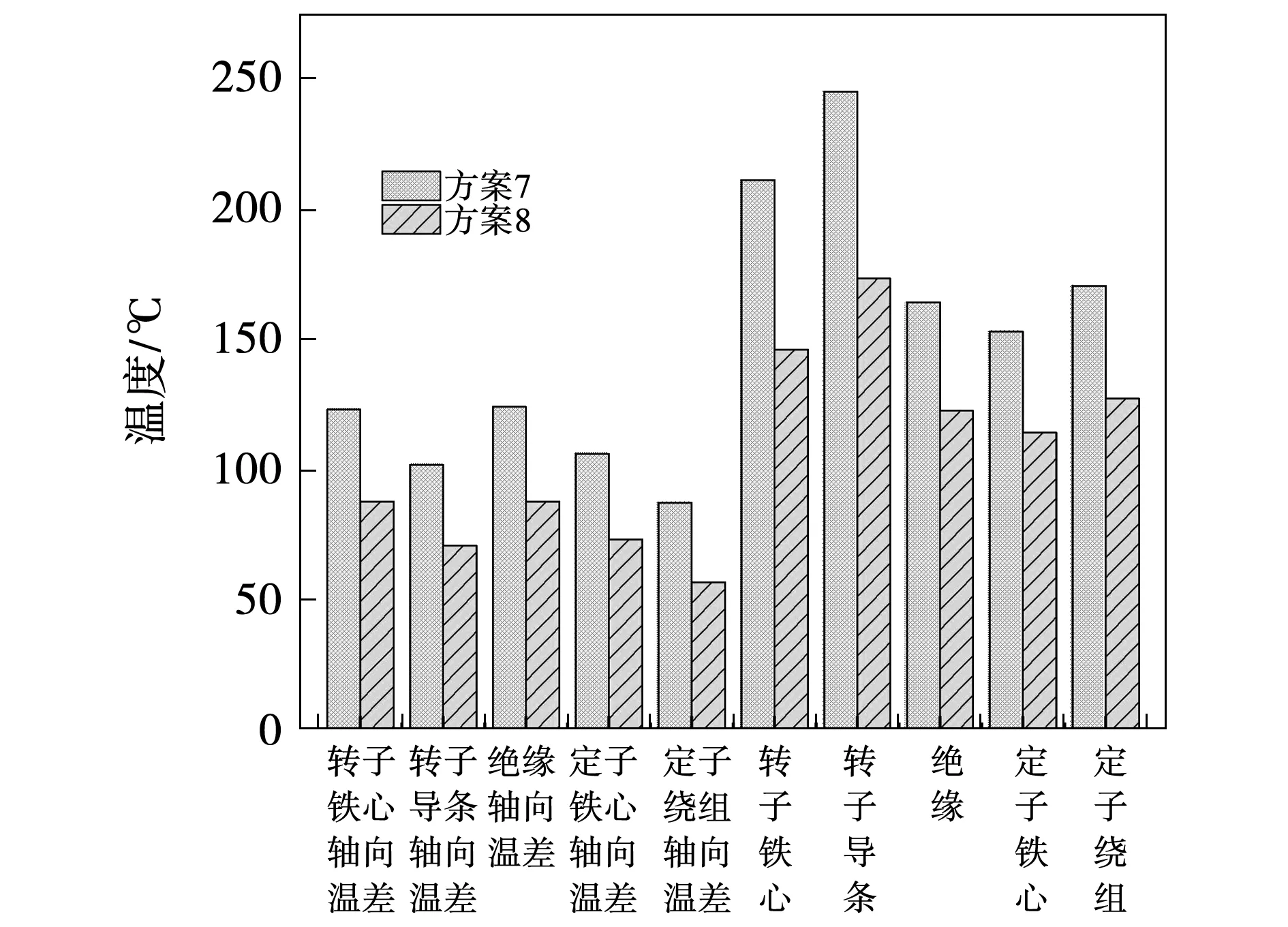
图14 方案8与方案7的温度对比结果Fig.14 Temperature comparison between scheme 8 and scheme 7

图15给出了方案7与方案8的定子通风孔和转子通风孔的风速对比，可以看出，与方案7相比，方案8靠近出口侧的定子通风孔和转子通风孔风速均显著增高，且风速在分段处均发生了阶跃升高。具体来看，定子通风孔内两方案起始位置风速相差较小，但方案8的定子通风孔内风速在分段处阶跃式增加到95 m/s，随着轴向位置的增加，风速最终稳定在83 m/s，平均风速比方案7提升78%。转子通风孔采用分段后，入风口侧风速减小，但在分段处风速也呈阶跃式增加，风速最终稳定在81 m/s左右，平均风速比方案7提升64%。

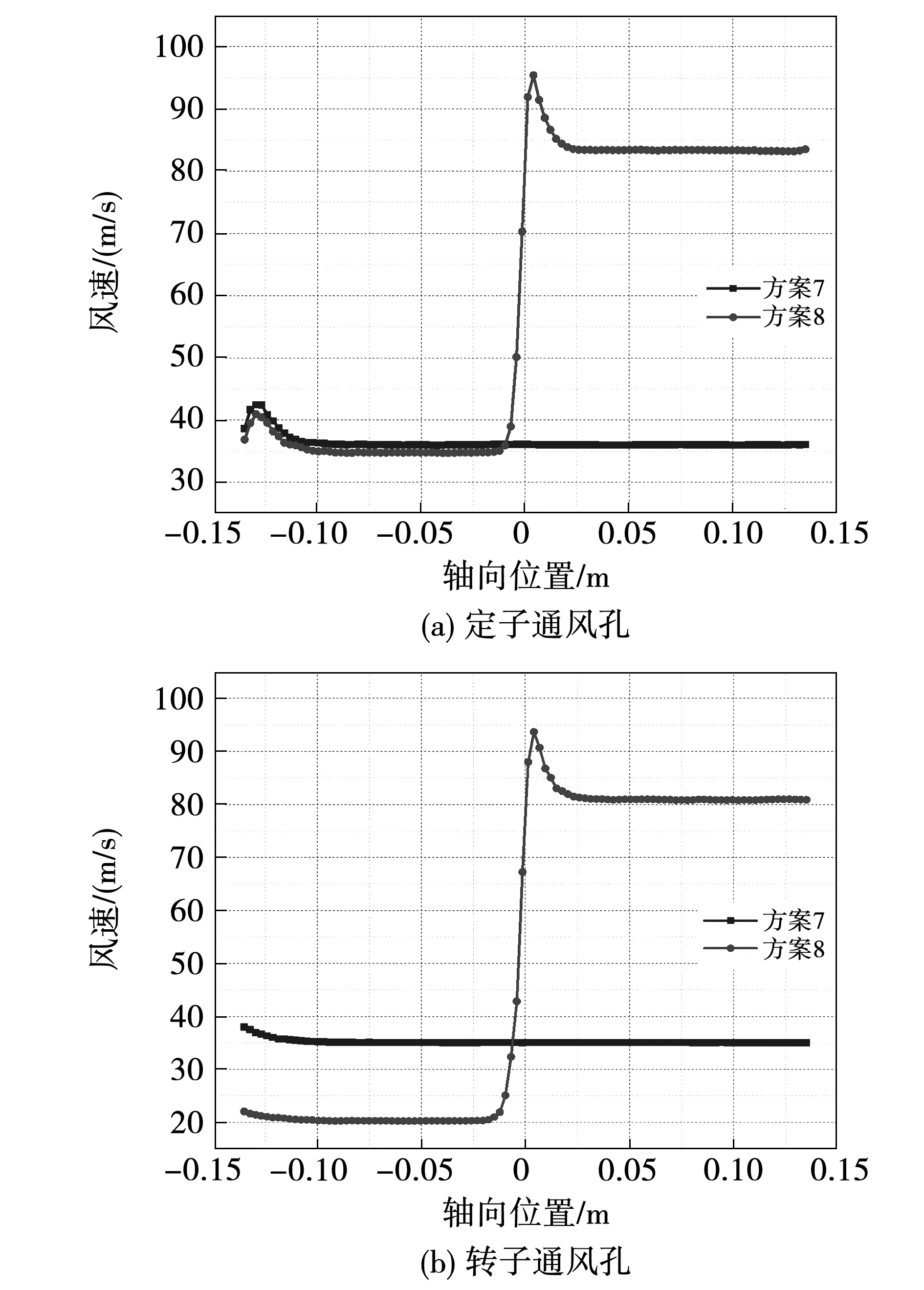
图15 方案7与方案8风速对比结果Fig.15 Velocity comparison between scheme 8 and scheme 7

方案8入风侧转子通风孔内风速变化更为明显，为了探究这一问题，提取方案7和方案8的流体域动压进行对比，结果如图16所示。可以看出，方案7的流体域压力分布较为均匀，轴向压力几乎无变化。而采用分段截面后，方案8的定子和转子通风孔内入风侧风压均有所下降，但转子通风孔入口侧风压下降幅度更大，出风口侧风压显著增加，同时气隙内风压约增加为原来的6倍。由此可见，分段通风结构使得电机流体域的风量分配发生了变化。

图16 方案7与方案8动压对比结果Fig.16 Dynamic pressure comparison between scheme 8 and scheme 7

综上所述，定转子通风孔采用分段处理后，流体域风压变化显著，导致出风口侧孔径较小的地方风速呈阶跃式增加，通风孔带走热量的能力变强，使得电机最高温度降低，从而有效减小了电机轴向温差。

由于上述分段定转子通风孔仅是在通风结构探索过程中结合文献[28]提出的，该结构并非该电机最优通风结构，在后续研究中需要进一步利用优化算法对电机的通风孔个数、孔径及分段数进行综合优化，找到有利于电机散热的最优解。

4 结 论

本文对600 kW的高速列车异步牵引电机进行流固耦合仿真，得到以下结论：

1)减小孔径可有效降低电机绕组温度，但是当孔径减小到一定值时，定子部分温度下降不再明显，但转子部分温度仍继续减小。此外，孔径的选取还需要考虑电机轻量化等因素，需要在保证满意的通风效果的前提下优先选择孔径大的通风孔；

2)在保证定子通风体积不变的前提下，将定子通风孔修改为正对定子槽的结构可有效减小定子绕组、定子铁心和绝缘的温度；

3)定子通风孔和转子通风孔采用分段处理后，降温效果明显。通风孔内风速在分段处阶跃式增加，通风孔内平均风速显著提高，有效降低了电机温度，从而平衡了轴向温差。