非理想磁链永磁同步电机转矩脉动抑制

郭鸿浩， 曹睿， 林欣欣， 张文峰

(南京邮电大学 自动化学院、人工智能学院，江苏 南京 210023)

0 引 言

永磁同步电机具有体积小、效率高、功率密度高、转动惯量比高以及调速范围宽等优点，如今被广泛应用于航空航天、高精度数控机床、机器人、电动汽车驱动等领域[1-3]。然而，在PMSM驱动系统中，由于电机存在齿槽效应和转子磁极结构引起的气隙磁场畸变，同时逆变器存在死区时间、管压降等非线性特性，电机将产生较大的转矩脉动，从而使电机系统产生振动和噪声，甚至会损坏转轴等机械结构件，对高精度场合的应用存在不利的影响[4]。因此，如何有效地抑制转矩脉动一直以来是研究的热点问题。

目前抑制转矩脉动的方法主要分为两个方向。第一种是从电机本体入手，对电机的本体结构进行优化，从而减少气隙磁场的谐波和齿槽转矩影响[5-6]，例如：定子斜槽或转子斜极、优化电机绕组类型、优化定转子磁路等。另一种是从控制策略入手，通过优化定子电流来抵消转矩中的谐波分量，从而使转矩输出更加平滑。这种方法不需要改变电机的本体结构，可以灵活地应用在不同的电机驱动系统中，因此具有更广阔的应用前景与研究意义。

一直以来，为了获得优化定子电流指令，国内外的研究学者们提出了一系列的方法。文献[7]使用了梯度下降算法，文献[8-9]设计了迭代学习控制器，通过对速度闭环控制系统做出改进，用新的控制器代替传统速度环PI控制，从而减小速度与转矩脉动。以上方法中并未考虑谐波电流的影响，电流控制仍采用传统PI控制，因此转矩脉动抑制效果有限。文献[10]推导了考虑谐波磁链的转矩模型，在此基础上建立了三相电流的几何模型，并设计了神经网络算法计算最优定子电流。文献[11]用LaGrange乘数法作为优化算法推导出了最优谐波电流的解析式。文献[12]建立了包含三目标的目标函数，并采用遗传算法寻找最优谐波电流。这些抑制方法都需要根据转矩模型经过复杂的公式推导，计算出谐波转矩的幅值并作为约束对象进行最优电流寻优。由于解析计算的复杂性，推导过程都忽略了谐波磁链相角的影响，降低了其结果的精确性和适用性。

为解决上述问题，提出了一种考虑谐波磁链相角的非理想磁链PMSM转矩脉动抑制方法，该方法用数值序列拟合出转矩的波形，将一个电角度周期内的转矩峰峰值作为优化对象，无需推导出谐波转矩的幅值，有效降低了计算复杂性。此外，该方法考虑了电机损耗的问题，建立了多目标函数，能够同时保证转矩脉动和损耗的最小化。最后，通过实验对所提抑制方法进行了有效性验证。

1 非理想磁链PMSM电磁转矩分析

根据磁共能模型[13]，PMSM的电磁转矩可以表示为

te=Kp[λdiq-λqid+(Ld-Lq)idiq+

(1)

式中：te为PMSM的总转矩；Kp=3p/2，p为电机的极对数；λd、λq分别为d、q轴转子永磁磁链；id、iq分别为d、q轴定子电流；Ld、Lq分别为d、q轴电感；θe为电角度；tcog为齿槽转矩。

为了便于分析PMSM数学模型，通常会假定转子磁链正弦分布于气隙中。但实际情况中，当磁链无法做到完全理想的正弦分布时，其将既包含直流分量也包含谐波分量。同时考虑到后续用电流的谐波分量来抑制转矩脉动，则λd、λq、id、iq可以用直流分量与谐波分量的和来表示，即

(2)

(3)

式中：λ0为d轴磁链的直流分量；λdh、λqh分别为d、q轴磁链的谐波分量；Id0、Iq0分别为d、q轴电流的直流分量；idh、iqh分别为d、q轴电流的谐波分量。

为了分析电磁转矩的构成分量，将式(2)、式(3)代入式(1)中并进行分类，则转矩可以表示为直流分量与谐波分量的总和，即

te=T0+th=T0+(th1+th2+th3+tcog)。

(4)

其中

T0=Kp(λ0Iq0+LΔId0Iq0)，

(5)

th1=Kp[λ0iqh+LΔ(Iq0idh+Id0iqh)]，

(6)

(7)

th3=Kp(λdhiqh-λqhidh+LΔidhiqh+

(8)

式中：T0为直流转矩；th=th1+th2+th3+tcog为谐波转矩；LΔ=Ld-Lq。

根据式(4)～式(8)可知，谐波转矩主要由四部分组成：th1表示仅由谐波电流引起的谐波转矩部分；th2表示仅由谐波磁链引起的谐波转矩部分；th3表示由谐波电流和谐波磁链共同作用引起的谐波转矩部分；tcog表示齿槽转矩。对于成品PMSM，其磁链和齿槽转矩均无法改变，因此谐波转矩th2和tcog是不可人为控制的，而th1和th3都与谐波电流有关，故可以通过调节定子谐波电流的方式来实现该部分转矩的控制。此外，分析式(6)～式(8)可见，转速的大小只会影响谐波转矩的频率，而不会对谐波转矩的大小造成影响。综上所述，抑制转矩脉动的核心思想便是寻找最优的定子谐波电流，使谐波转矩的可控部分与不可控部分相抵消，从而实现总谐波转矩的最小化。

2 最优谐波电流计算方法

2.1 转矩的序列表示

在使用优化算法寻找最优谐波电流之前，首先需要根据定子电流与转矩之间的约束关系建立目标函数。通常方法是将谐波磁链、谐波电流和齿槽转矩的具体展开式代入转矩公式，提取出转矩的幅值并使其最小。根据文献[14]，谐波磁链、谐波电流和齿槽转矩可以表示为

(9)

(10)

(11)

式中：λdk、λqk为d、q轴磁链的k次谐波幅值；φλdk、φλqk为d、q轴磁链对应次数谐波的相角；Idk、Iqk为d、q轴电流的k次谐波幅值；φidk、φiqk为d、q轴电流对应次数谐波的相角；Tck和φck分别为齿槽转矩的k次谐波幅值与相角。

将式(9)～式(11)代入式(4)，虽然可以得到谐波转矩的幅值与相位，但推导过程复杂，结果表现形式冗长，不利于构建目标函数。同时，推导过程中常常忽略了th3项的影响，且对谐波磁链的d、q轴相角进行了近似化处理。如文献[11]中为了便于提取谐波转矩的幅值表达式，将φλdk和φλqk皆取为0，与实际情况有偏差，这样使其计算结果只能反映特殊情况，不具有普遍性，极大地限制了该抑制方法的精确性和应用范围。

为了解决上述问题，可以用足够密集的数值序列来表示出谐波磁链和谐波电流的波形。在一个电角度周期中，将电角度θe的变化区间0～2π平均分成n等分，这样每一个角度都有一个对应的磁链与电流值，即可用一组n维数值序列将一个周期内的谐波磁链和谐波电流表示为

(12)

(13)

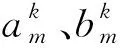
齿槽转矩也可以用一组n维序列表示，即

(14)

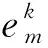
在PMSM中，谐波转矩的频率为6的整数倍基频[12]，对于不同次的谐波转矩，可以用相应次的谐波电流单独进行抑制。以k次谐波为例，将式(12)～式(14)代入式(1)，可以得到仅保留k次谐波时的转矩序列为

(15)

其中

(16)

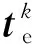
从式(15)中可以看到，转矩直接根据磁链和电流的序列获得，使用了最基本的转矩公式，不仅避免了复杂的公式推导过程，还考虑了磁链相角对转矩的影响，因此具有更高的准确性和适用性。

2.2 基于遗传算法的优化电流设计

PMSM的转矩脉动峰峰值可以表示为

(17)

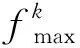
在PMSM转矩脉动抑制中，电流寻优的目标就是找到合适的谐波电流idh、iqh，使转矩波动的峰峰值最小。同时，谐波电流也会引起额外的损耗，损耗的大小与谐波电流幅值的平方和有关[15]，故电流寻优还需考虑减小谐波电流的平方和。此时，该优化问题包含两个目标函数，即

(18)

对于一个多目标函数优化问题，难以直接计算出优化结果。虽然可以采用类如LaGrange乘数法推导出最优谐波电流的表达式[11]，但前提是只有在对磁链相角进行近似化处理后表达式才成立。在考虑实际磁链相角的情况下，本文选择使用遗传算法进行谐波电流优化设计。将式(18)两个目标函数用一个函数来表示：

(19)

式中：k1和k2为权重系数，影响了各自目标在函数中所占的比重，数值越大，说明该项对总体结果的影响越大；x为函数的解，即包含了k次谐波电流的幅值Ikd、Ikq与相位φidk、φiqk。

基于遗传算法的最优谐波电流搜寻过程如流程图1所示。首先需要对种群进行初始化，参数设置参照遗传算法一般取值范围，并通过观察结果的收敛性进行适当调整。设置初始种群数N为100，且每一代种群总数均保持不变，设置最大迭代次数MAXGEN为200，交叉概率Pc和变异概率Pm分别为0.8和0.2，权重系数k1和k2分别为10和1。算法自动生成100组x作为第0代，并计算出各自的F(x)，将其中的最优解x储存。接着依次进行选择、交叉、变异的操作，从而产生新的子代，并计算出子代各自的F(x)，更新最优解。重复进行选择、交叉、变异，直至达到最大迭代次数，输出此时储存的最优解。

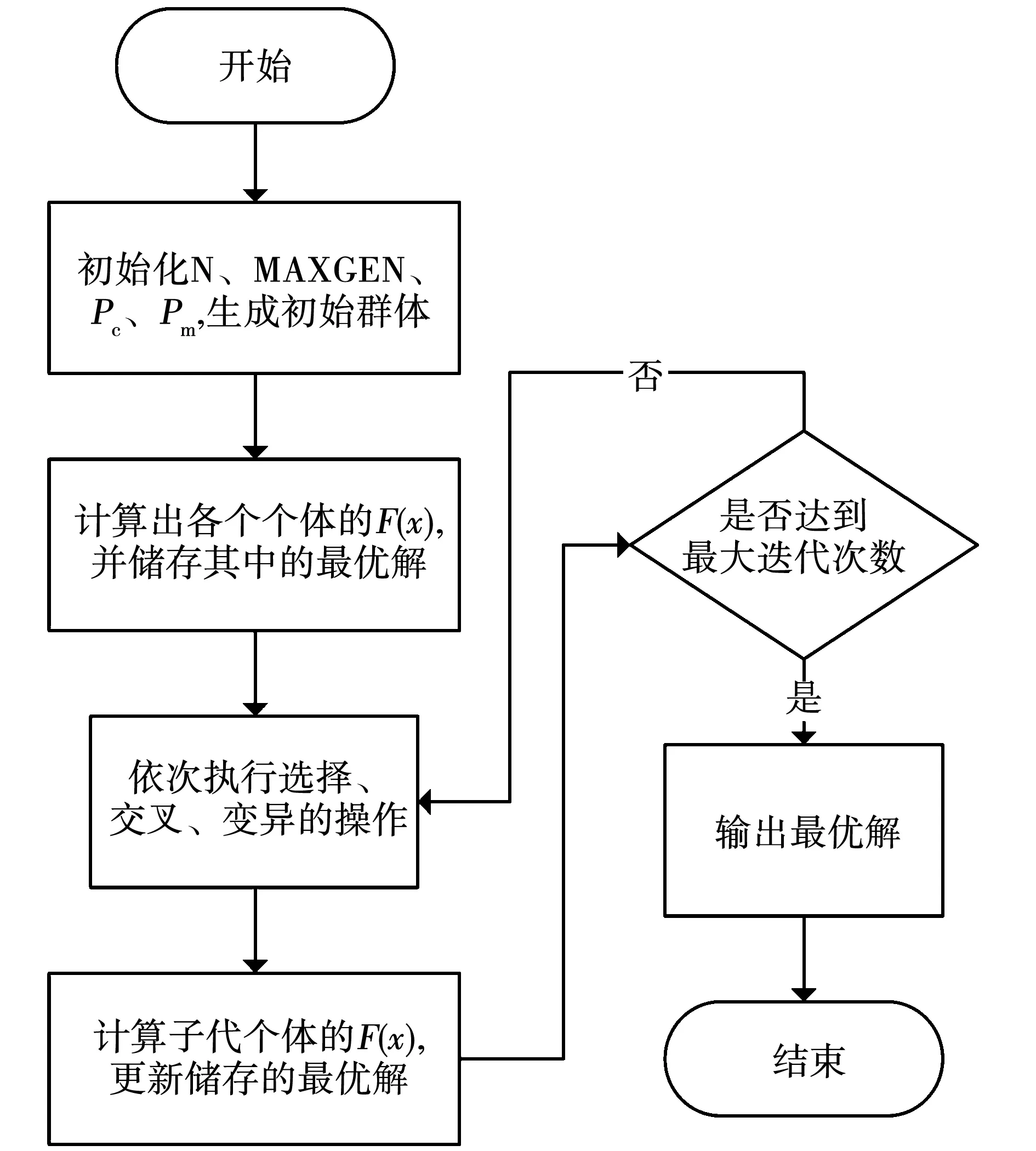
图1 基于遗传算法的最优谐波电流搜寻流程图Fig.1 Optimal harmonic current searching flow chart based on genetic algorithm

图2给出了Id0=0 A，Iq0=6.75 A时遗传算法的计算结果。图2(a)结果表明，经过迭代，最终F(x)的值明显降低且趋于稳定。此时，对应最优谐波电流时的单周期转矩理论波形如图2(b)所示，转矩波动只有0.04 N·m。将该组最优解作为谐波电流的给定值注入电机，便可以实现转矩脉动的抑制。

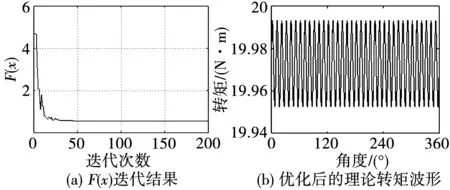
图2 遗传算法计算结果Fig.2 Result of genetic algorithm

3 最优谐波电流控制系统设计

根据以上分析建立PMSM最优谐波电流控制系统，其原理图如图3所示。

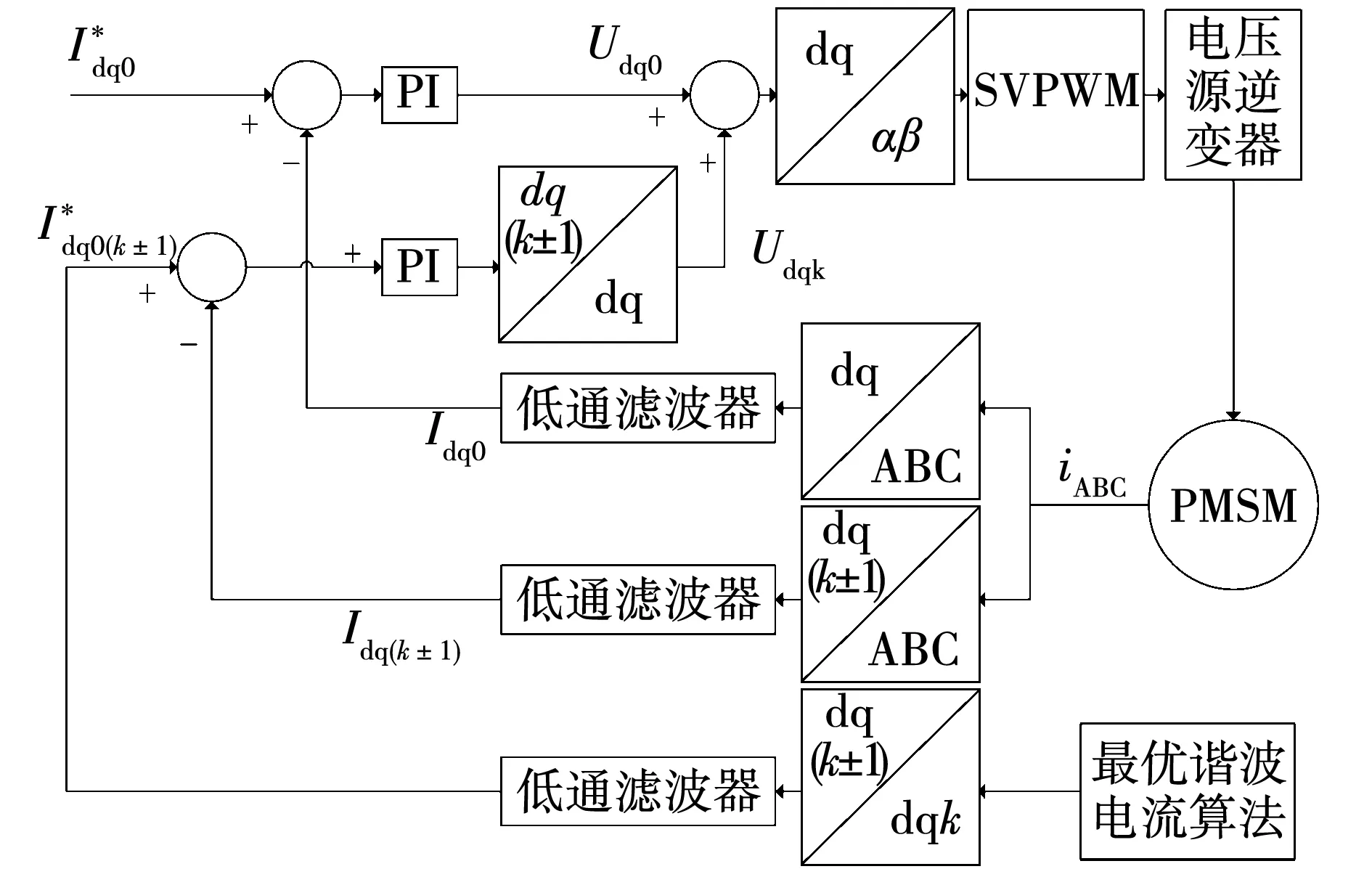
图3 最优谐波电流控制系统原理图Fig.3 Schematic diagram of optimal harmonic current control system

从图3中可以看出，d、q轴参考电流包含了直流给定值和谐波给定值两部分。其中，直流给定值由系统的速度环输出决定，谐波给定值则由遗传算法根据电机当前的运行工况获得。为此，需要设计两个独立的电流控制器。由于PR控制器的控制效果受离散化方式影响，不便于设计，而多同步旋转PI控制器只需要经过一系列的坐标变换即可实现谐波电流的跟踪控制，因此本文采用多同步旋转PI控制器[16]。首先，对实际电流和参考电流进行谐波坐标变换，并使用低通滤波器提取出它们各自在该次坐标系上的直流量。然后，在不同次坐标轴上分别使用PI控制器使实际电流跟踪参考电流，产生谐波电压信号Udqk。最后，将谐波电压信号应用于逆变器控制，实现转矩脉动的抑制。

当电机处于稳态运行时，其转矩波动呈现为幅值稳定的周期变化，因此对于每一个稳态，都有一组与之相应的最优谐波电流。在实际应用中，可以通过遗传算法预先算出不同负载状态时的最优谐波电流，生成一组查找表。当电机运行时，只要根据查找表选择当前的最优谐波电流，这样大大简化了系统在线计算流程，更易于实现系统的实时控制。

4 仿真及实验验证

4.1 仿真分析

本文对所提出的转矩脉动抑制方法首先进行了仿真验证。在MATLAB/Simulink中搭建了系统的仿真模型，系统结构图如图3所示，最优谐波电流算法目标函数如式(19)所示，其中k1=10、k2=1。仿真中电机参数设置与实验电机参数一致，如表1所示。

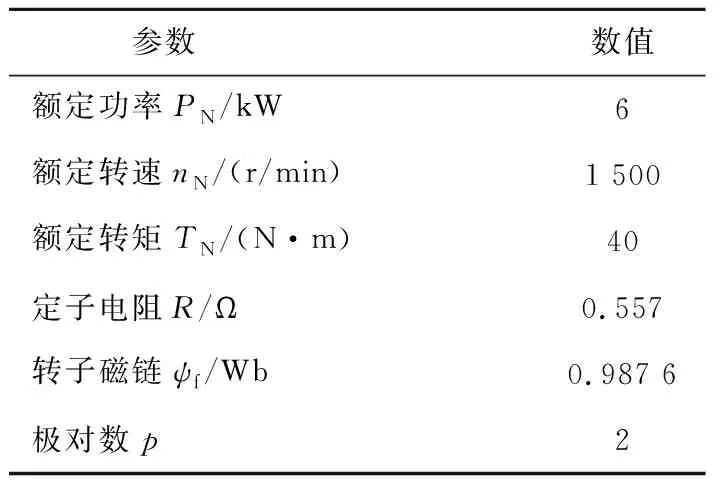
表1 永磁同步电机参数

该实验待测IPMSM中谐波磁链的主导分量为18次谐波，因此为方便说明所提出转矩脉动抑制方法的效果，仿真及实验主要针对18次的转矩脉动进行抑制。分别对负载转矩为20 N·m和40 N·m时，加入抑制算法前后的仿真结果进行分析。

图4给出了转速为1 500 r/min额定转速，负载转矩为20 N·m时的仿真结果。通过仿真结果可以看出，未施加抑制策略时电压与电流谐波较小，转矩脉动约有10%。采用遗传算法计算当前稳态工况下的最优谐波电流，此时算法输入为Id0=0 A，Iq0=6.75 A，输出18次谐波电流幅值Id18、Iq18分别为-0.190 7 A和-0.338 0 A，相位φid18、φiq18分别为3.749 7 rad和0.981 9 rad。施加抑制策略，将最优谐波电流注入控制系统后d、q轴电流上叠加高次谐波，转矩脉动峰峰值由2.03 N·m降低为0.12 N·m。

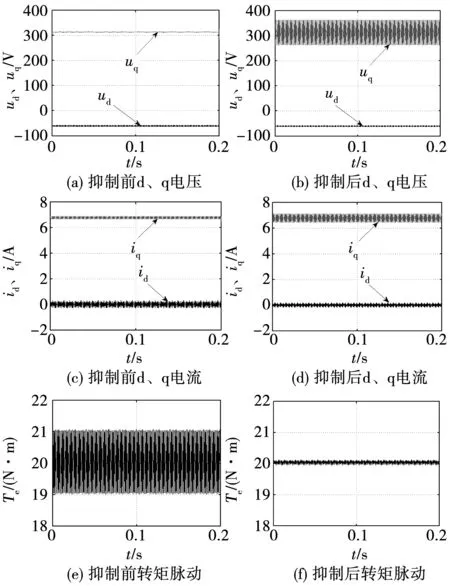
图4 负载转矩20 N·m时仿真结果Fig.4 Simulation results when load is 20 N·m

图5给出了同样转速下，负载转矩为40 N·m时的仿真结果。由于工况发生改变，此时算法的输入发生改变，输入变为Id0=0 A，Iq0=13.5 A，得出该工况下18次谐波电流幅值Id18、Iq18分别为0.524 9 A和-0.663 6 A，相位φid18、φiq18分别为0.987 3 rad和1.114 7 rad。通过施加转矩脉动抑制策略，转矩脉动峰峰值由3.82 N·m降低为0.79 N·m，具有显著的转矩脉动抑制效果。

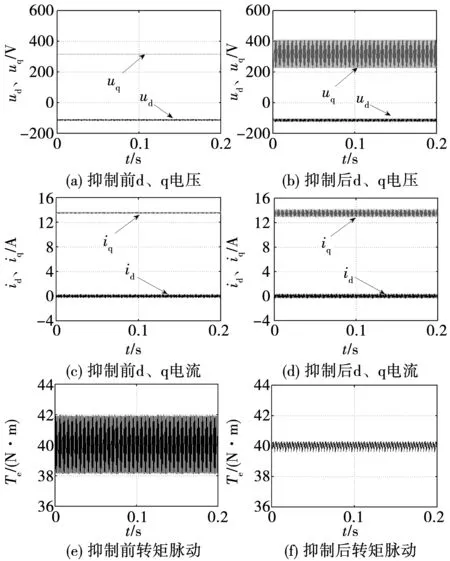
图5 负载转矩40 N·m时仿真结果Fig.5 Simulation results when load is 40 N·m

4.2 实验结果

实验平台如图6所示。该平台包含被测电机、光电编码器、转矩传感器、逆变器、负载电机以及伺服控制器。其中，被测电机为内置式PMSM(IPMSM)，具体参数如表1所示。伺服控制器采用Opal-RT实时仿真控制器，该控制器中运行着由仿真模型编译成的算法，并与硬件电路相连实时采集信号，可以通过上位机进行控制和观测。

图6 实验平台实物图Fig.6 Photograph of experimental platform

与仿真工况相对应进行实验分析，在1 500 r/min的额定转速下进行两组实验，分别给出了负载转矩为20 N·m和40 N·m时加入抑制算法前后的实验结果。需要指出，实验中考虑到算法计算量大，存在延迟，因此通过离线计算预生成查找表，所采用目标函数与仿真一致，实际实验时最优谐波电流通过查找表确定。

启动电机至额定转速1 500 r/min，施加20 N·m负载转矩待电机运行至稳态，此时即未施加抑制策略时的d、q轴电压与电流稳态波形如图7(a)、图7(b)所示。

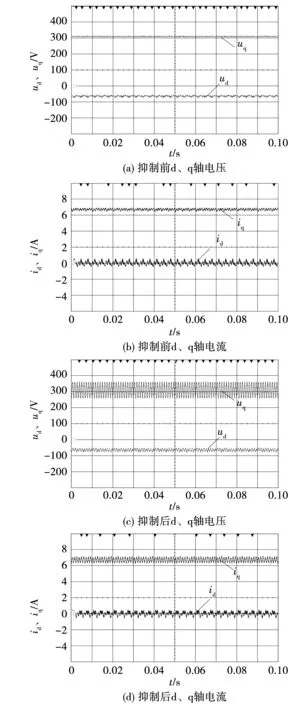
图7 20 N·m时抑制前后d、q轴电压与电流稳态波形Fig.7 dq-axis voltages and current before and after torque minimization when load is 20 N·m

电流的跟踪控制通过对实际电流进行采样，比较实际电流与参考电流的误差并送入电流控制器，最终将电流控制器输出的参考电压即d、q轴电压注入空间电压矢量调制器实现。可以看到，此时由于未施加抑制策略，最优谐波电流尚未注入，PI控制器仅能对电流中的直流分量进行控制，因此电流控制器输出的d、q轴电压中谐波分量较少。施加抑制策略，待注入最优谐波电流幅值Id18、Iq18分别为0.115 5 A和0.322 1 A，相位φid18、φiq18分别为1.503 7 rad和4.093 1 rad，注入后d、q轴电压与电流稳态波形如图7(c)、图7(d)所示。从图中可以看出，此时d、q轴电流上叠加高次谐波，相应的d、q轴参考电压也会产生很大的高次谐波以保证谐波电流的跟踪，与仿真结果吻合。此外，实验时开关频率为20 kHz，需要注入的谐波电压为900 Hz，由于开关的非线性，会使得注入的电压产生一定的失真。

图8为负载转矩20 N·m时施加抑制策略前后的转矩波形。从图中可以看出，抑制前转矩脉动峰峰值为2.54 N·m，施加抑制策略后，转矩脉动峰峰值为0.82 N·m，降低了67.71%。实验中转矩脉动大于仿真结果，是由于仿真建模时仅考虑了18次的谐波，而实际电机还存在6次、12次等频次谐波。

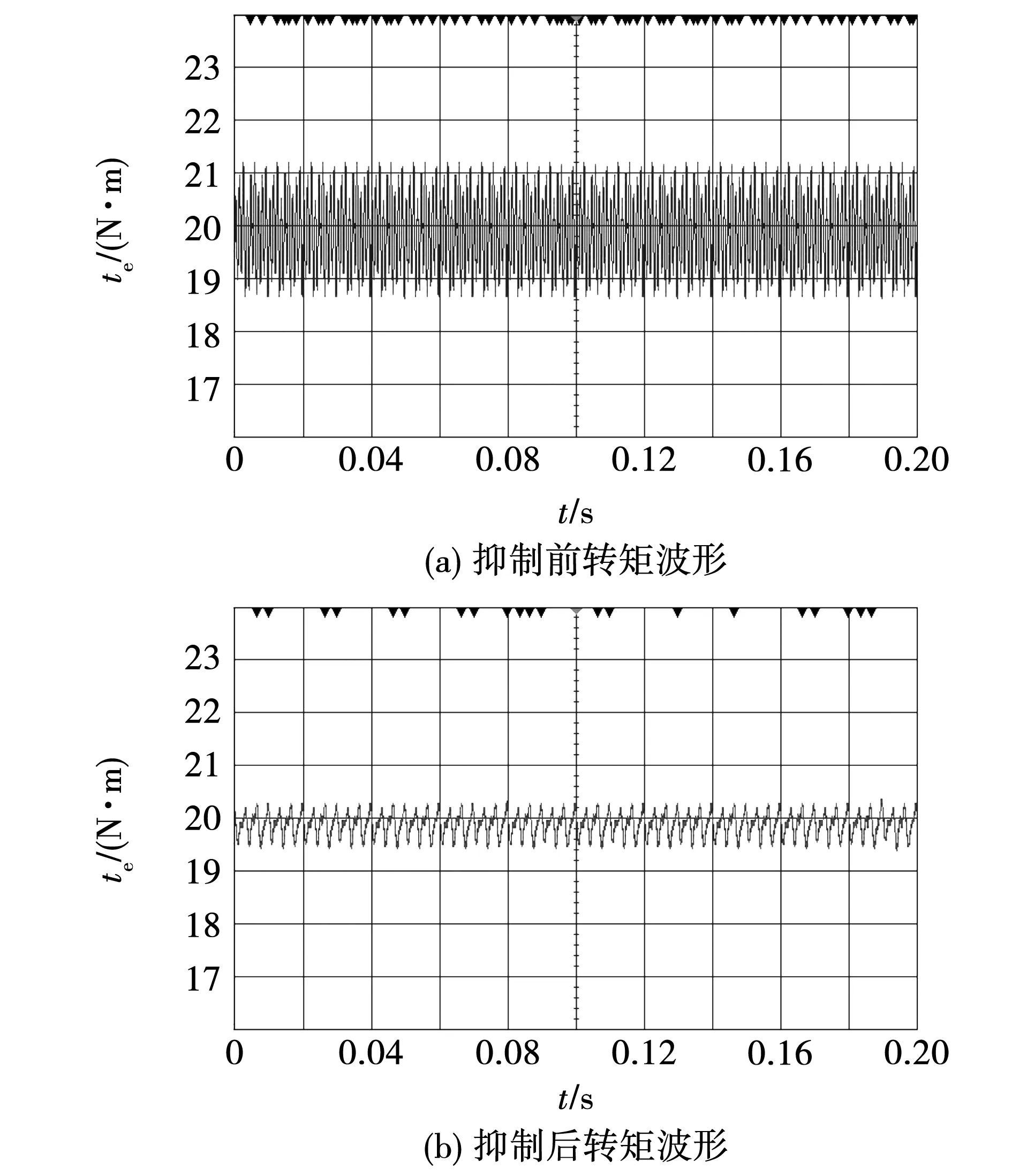
图8 20 N·m时抑制前后转矩稳态波形Fig.8 Measured torque before and after torque minimization when load is 20 N·m

将负载转矩增加为40 N·m，待系统进入稳态后，d、q轴电压与电流稳态波形如图9(a)、图9(b)所示，此时尚未施加抑制策略。注入该工况下的最优谐波电流，幅值Id18、Iq18分别为-0.324 5 A和0.732 8 A，相位φid18、φiq18分别为1.976 9 rad和4.001 0 rad。注入后的d、q轴电压与电流稳态波形如图9(c)、图9(d)所示。

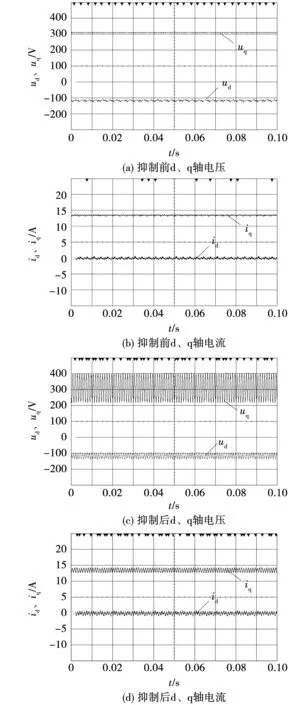
图9 40 N·m时抑制前后d、q轴电压与电流稳态波形Fig.9 dq-axis voltages and currents before and after torque minimization when load is 40 N·m

图10给出了负载转矩40 N·m时施加抑制策略前后的转矩波形。可以看到，施加抑制策略后，转矩脉动峰峰值由4.83 N·m减小为1.66 N·m，降低了65.63%，与仿真结果吻合。以上实验结果表明，基于遗传算法的永磁同步电机转矩脉动抑制方法通过注入额外的谐波电流产生额外的谐波转矩，与已有的谐波转矩相抵消，能有效地降低转矩脉动。

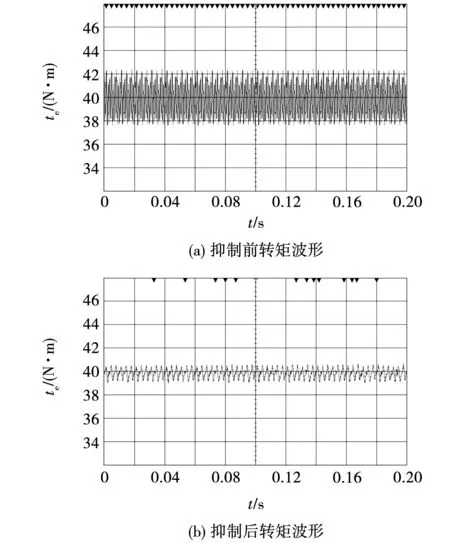
图10 40 N·m时抑制前后转矩稳态波形Fig.10 Measured torque before and after torque minimization when load is 40 N·m

5 结 论

本文针对PMSM驱动系统的转矩脉动问题，设计了一种考虑谐波磁链相角的PMSM转矩脉动抑制方法。通过理论分析和实验验证，得出以下结论：

1)采用序列表示谐波磁链、谐波电流及谐波转矩，能反映磁链相角对谐波转矩的影响。该方法能够准确反映转矩的变化，同时也避免了复杂的公式推导；

2)遗传算法根据不同的工况计算出相应的最优谐波电流，通过离线计算生成最优谐波电流查找表，使该方法可以很好地适用于不同的工况；

3)实验结果显示，采用本文所提出的转矩脉动抑制方法，转矩脉动减少了约67%，具有很好的转矩脉动抑制效果。