油纸绝缘典型缺陷局放特性及缺陷类型识别

池明赫， 夏若淳， 罗青林， 张潮海， 曹津铭， 关毅， 陈庆国

(1. 哈尔滨理工大学 工程电介质及其应用教育部重点试验室，黑龙江 哈尔滨 150080；2.特变电工股份有限公司，新疆 昌吉 750306；3. 哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150006)

0 引 言

油浸式变压器因其具有良好的电气与机械的性能，作为关键设备被广泛应用于高压电网[1-2]。油浸变压器内绝缘主要是油纸组合绝缘，变压器纸质绝缘件在制造、装配或运行过程中可能出现气隙、金属颗粒等缺陷。各类缺陷使得绝缘内部的电场分布出现畸变，引发局部放电，进而对变压器绝缘造成损伤，对变压器的运行寿命产生影响[3-5]。有研究资料表明，变压器安全事故中很大部分是因绝缘缺陷造成的[6-7]。因此，应对变压器进行有效的局部放电检测，在事故发生以前及时发现故障并进行排除[8-10]。

目前因国内外学者在局部放电的研究对象与测量方式的不同，其分析与识别局部放电信号的方法也不尽相同。目前采用的机器学习的方法主要有K-邻近法(K-nearest neighbors,KNN)[11-12]、决策树与随机森林(decision tree and random forest,DT&RF)[13]、K均值聚类分析法(K-means)[14]与支持向量机(support vector machine,SVM)[15]等。目前较为常见的方式是对局部放电图谱包含的各类特征统计参量进行特征提取再运用机器学习的对局部放电信号进行分析[16]。浙江大学的杜浩等人研究了直流电压下的交联聚乙烯电缆的三种典型缺陷模型的局部放电特性，并通过局部放电参数的时域图谱，提出四类统计特征图谱以进行表征[17]。X.Peng等人提出了一种可用于电缆检测系统的方法，该方法基于K-means方法且无需相位参考信息即可识别局部放电的模式[18]。朱永利等人以SVM回归代替基于变量预测模型的模式识别方法(variable predictive model based class discriminate,VPMCD)中原有的多项式回归，以样本之间预测最小误差平方和最小为依据进行放电模式识别，解决了原有方法对高维度小样本数据预测精度差的问题，结果表明其较传统的SVM与VPMCD方法的更为优秀[19]。N.Pattanadech与Y.Zang等人运用主成分分析与KNN相结合的方法对局部放电类型进行识别，并研究了不同训练集与测试集比例下的识别精度[20-21]。秦雪等人运用二维Littlewood-Paley经验小波变换的特征提取方法，分解四种电缆绝缘缺陷的φ-q-n局部放电图谱，得到小波系数子图并对其特征值进行提取，得到了相较传统方法的更高精度的识别效果[22]。

以上常用的局部放电识别算法均属于传统机器学习范畴的算法。传统的机器学习方法因其结构上过于简单而需要提取更有效的特征量来解决实际问题[23]，同时也无法通过对训练数据集的增加来对其进行持续改进[24]。因此其在运用层面已经落后于当前主流的深度学习，深度学习因需求少、功能性优化且能借助大数据以及算法和硬件的革命以实现更高的性能而受到了越来越多的关注[24]。深层神经网络(deep neural networks，DNN)是深度学习中基础的网络结构形式，其被广泛应用于其他各领域，它是从传统人工神经网络中的反向传播神经网络(back propagation neural networks，BPNN)演变而来的。因不同研究对象及不同类型的局部放电性状不同，基于DNN的识别效果也不同，但是却少有基于上述情形而对DNN参数与结构的研究，尤其是针对变压器油纸绝缘的局部放电类型识别问题上的优化。

为此，本文提出一种基于局部放电信号及深层神经网络的油纸绝缘缺陷分类方法，以不同缺陷试样在任意局部放电阶段下的局部放电信号的特征算子作为模式识别的特征参量，利用DNN网络实现油纸绝缘缺陷的类型识别。同时，本文探究DNN参数对于识别效果的影响，得到最适合于变压器纸质绝缘件内部局部放电识别的DNN模型并与传统及其学习方法对比了识别效果，验证所提方法有效性。

1 试验方法

1.1 试验平台及电极

本试验在局部放电屏蔽室内进行，按照图1所示搭建局部放电测试系统。该局部放电测试系统主要包括调压器T0，无局放试验变压器T1，保护电阻R1，分压器R2C1、R3C2，耦合电容器Ck以及检测阻抗Zm和采集系统X1。

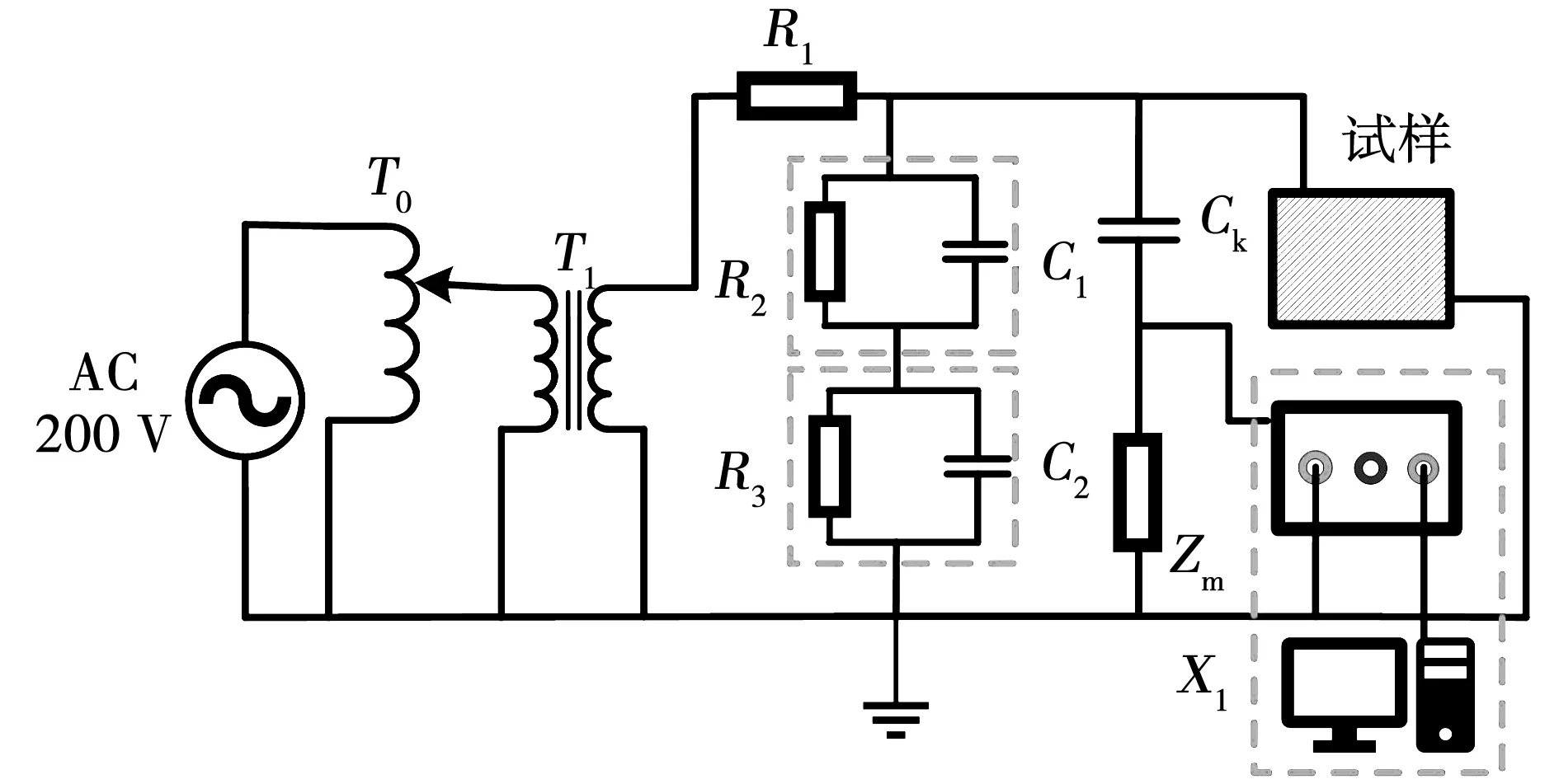
图1 试验电路图Fig.1 Diagram of test circuit

根据测量标准IEC60243-1:1998，本次试验使用柱板电极，其中柱电极直径为25 mm，附带半径为3 mm的边缘倒角，板电极为直径80 mm的圆盘，电极尺寸图与实物图如图2所示。

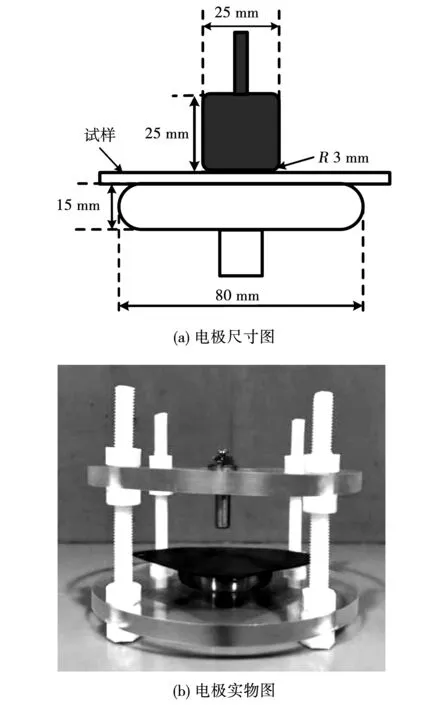
图2 柱板电极示意图Fig.2 Schematic diagram of column-plate electrodes

1.2 缺陷模型的制作及加压方式

本试验依照实际工程运行条件下出现的缺陷类型制备了无缺陷纸板、含气隙缺陷纸板和含金属杂质纸板进行局部放电测试，分别对应模拟纸质绝缘件内无缺陷但设计或制造不合理导致的油中放电、绝缘件内含气隙以及含金属杂质导致的绝缘件内部放电。仿照目前工程上制备电气绝缘纸板的方式，以电工级的未漂针叶木材硫酸盐纸浆为原材料，经纸浆打浆、疏解、称取、沥水操作后，在纸板未干燥时把纸板分成两份，将聚酯膜置于两张湿纸板之间，进行压榨和烘干，抽去聚酯膜制成含气隙缺陷纸板试样；制作含金属杂质纸板时将上述过程中的聚酯膜替换为金属薄片，且压制烘干后将金属片留在纸板中，试样尺寸如图3所示。

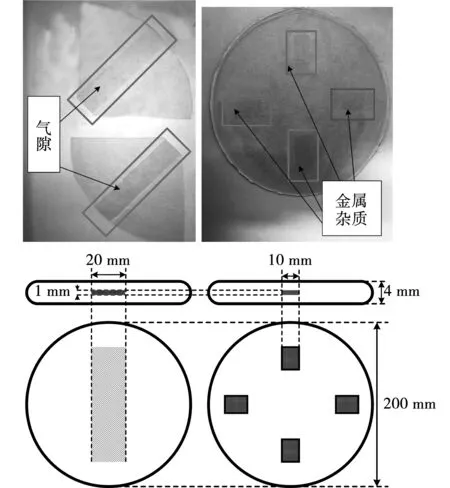
图3 缺陷尺寸图Fig.3 Diagram of defect size

升压方式上采用恒压法与阶梯升压法结合的升压方式[25-26]。首先，以每次2 kV的步长开始升压，每次进行一次升压操作后维持该电压5 min，以观察局部放电信号是否出现(选取3 pC作为起始局放量)。记录下首次出现局部放电信号时的电压值，然后再以每次2 kV的速率升压至上述电压的1.5倍数值附近后获取较为稳定的局部放电信号。

1.3 局部放电信号采集与处理

选取尺寸相同的3种试样模型进行局部放电试验，并从放电起始时刻至临近击穿时刻随机采集数据，总共1 200组放电信号数据。按着上述试验方式采集到的无缺陷纸板、含气隙纸板和含金属杂质缺陷纸板各自在不同阶段的局部放电二维图谱如图4所示。从图4的局部放电图谱可以看出，这3种局部放电信号图谱具有一定的相似性，难以通过直观识图判断是何种缺陷导致的放电，应用智能识别算法是解决该问题的有效途径。

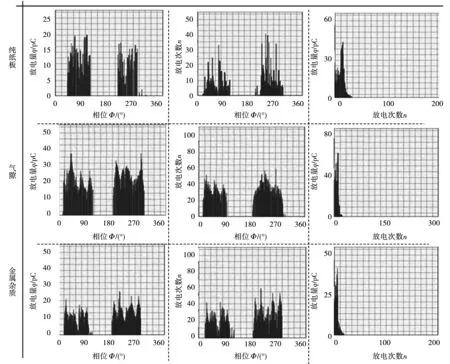
图4 试样局部放电特性图Fig.4 PD characteristic diagram of sample

随着统计学在高压与绝缘领域上的应用，基于放电统计图谱的局部放电类型识别成为了当前研究的热点，通过对局部放电的各类图谱进行统计特征提取，得到能够定量描述图谱形态及其变化情况的特征参数，能够很大程度上提升对局部放电的模式识别的效果[27-28]。常用的统计参数有偏斜度Sk、峭度Ku、不对称度Asy、互相关系数CC以及Weibull参数α、β。偏斜度与峭度分别代表图谱的偏斜程度和图谱分布特性，不对称度代表放电量相对于相位的不对称度；互相关系数用以表征不同类型图谱在正负半周上的形状分布相似程度，Weibull参数α为图像的尺度参数、β为图像的形状参数。以上参数的计算公式如表1所示，所提取到的统计参数如表2所示。

表1 统计特征量参数

表2 用于局部放电识别的特征量

提取的部分特征参数如图5所示，通过对3种试样的部分特征参量的比较可以看出，它们的特征量在整体分布上没有明确的规律，同时其分散性不佳，因此不能直接用其进行局部放电类型的识别。鉴于神经网络方法在分类与聚类问题已有一定规模的运用，其效果远高于人工识别分类。将局部放电图谱统计参数与深层神经网络结合，对不同缺陷局部放电进行识别。

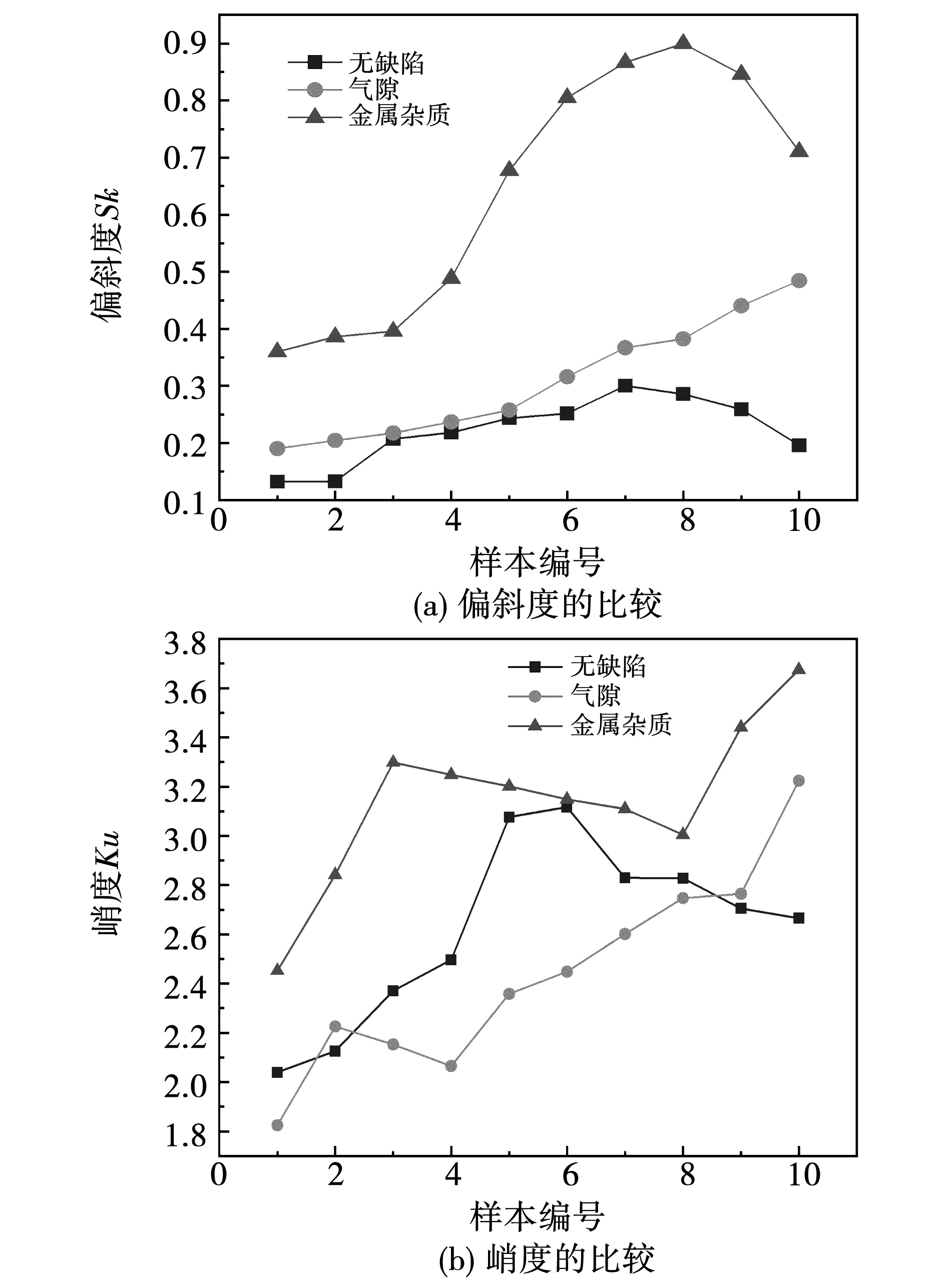
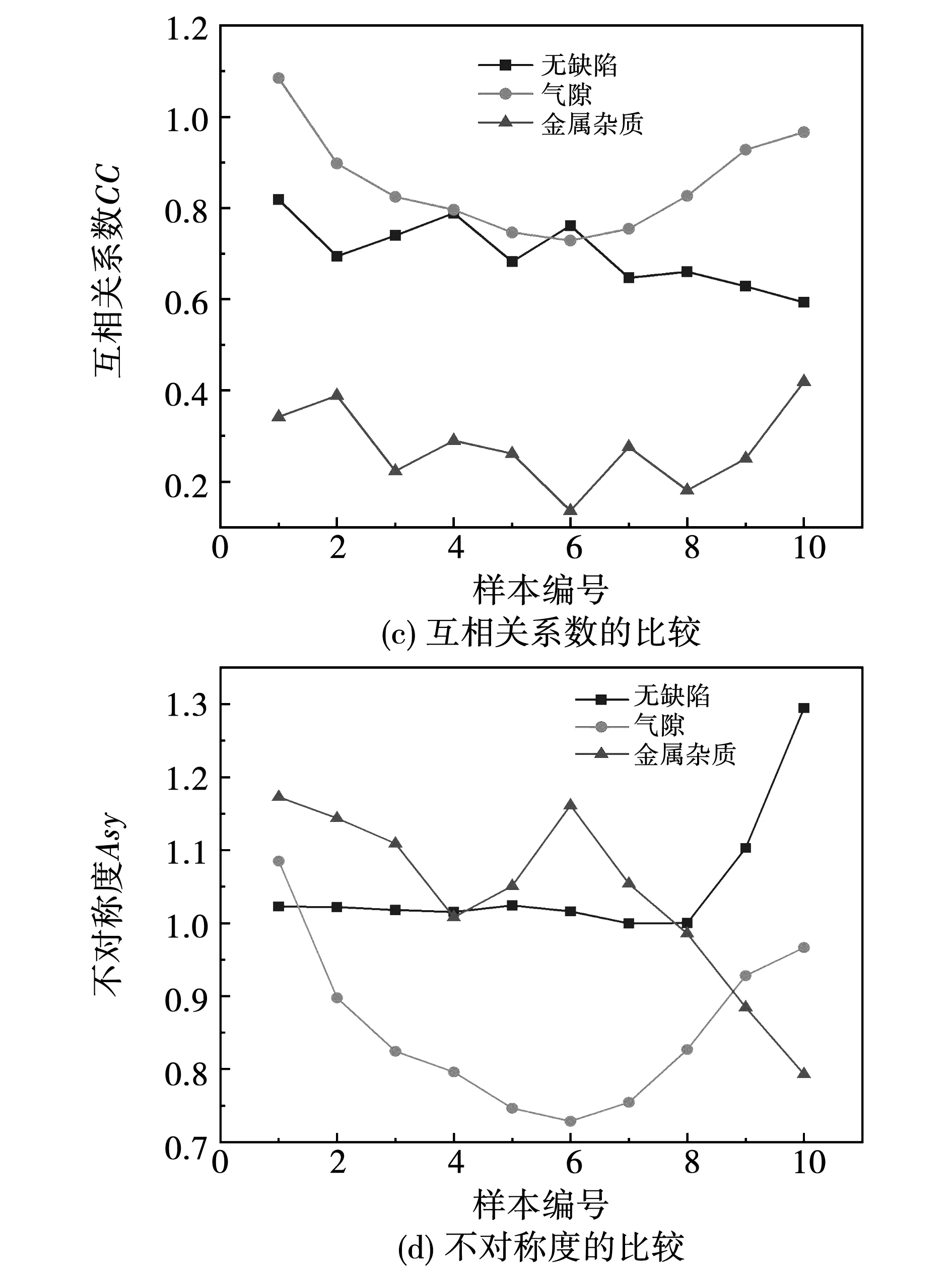
图5 不同试样的部分统计特征量比较Fig.5 Comparison of partial statistical features of different samples

2局部放电模式识别

2.1 深层神经网络的结构与运行

深层神经网络的结构包括输入层、隐含层以及输出层。深层神经网络相比于BP神经网络具有更多的隐含层，使得深层神经网络具有更优异的非线性模拟能力与特征学习能力[29]。在FAN Fenglei等人[30]的启发下采用了一种三阶神经元的深层神经网络，其较单阶神经元具备更优异的非线性模拟能力，同时不像更高阶神经元那样引起过拟合，其结构如图6所示。

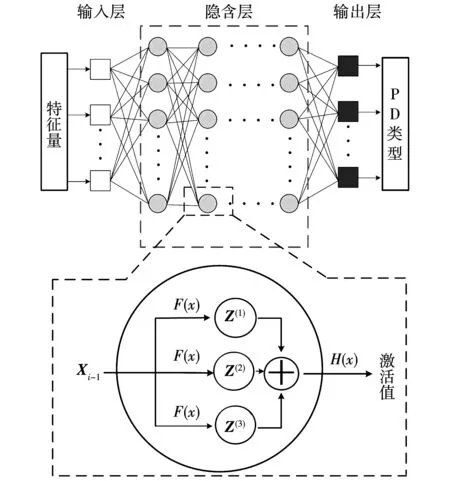
图6 深层神经网络与三阶神经元Fig.6 Structures of DNN and the three-order neuron

深层神经网络的前向运算为输入值向量x与权值矩阵W以及偏差向量b进入神经元后通过激活函数F(x)的运算获得激活值的过程。从输入层开始逐层运算，上一层的输出值作为下一层的输入，在神经元中进行运算并产生新的输出矩阵Z，依此层层运算至输出层并得到输出为止。表达式为

Zi=F(Wi·xi-1+bi)。

(1)

式中：Zi表示第i层的输出向量；Wi表示上一层连接第i层的权值矩阵；xi-1表示来自第i-1层的输出向量；bi表示第i层的偏差向量；F(x)表示激活函数，由于Tanh函数具有较好的非线性拟合特性，神经元内处理目的是让神经元具有更强的非线性拟合能力，因此在此采用Tanh函数。

在上述基础上使用三阶神经元，其使神经元内每个预激活值被分别激活三次，以获得更好的非线性模拟能力，其表达式为：

(2)

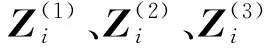
2.2 深层神经网络的参数寻优

神经网络的误差优化算法、学习率以及隐含层层数会对神经网络运行的迭代速度与误差下降速率产生影响，进而影响识别过程中的识别效率。因此对影响神经网络分类的因素进行对比，从而寻找变压器纸质成型件的局部放电类型识别的最适合神经网络模型。将总共采集到1 200组数据以8∶2划分为训练数据集与测试数据集，以图7所示的流程运行神经网络。

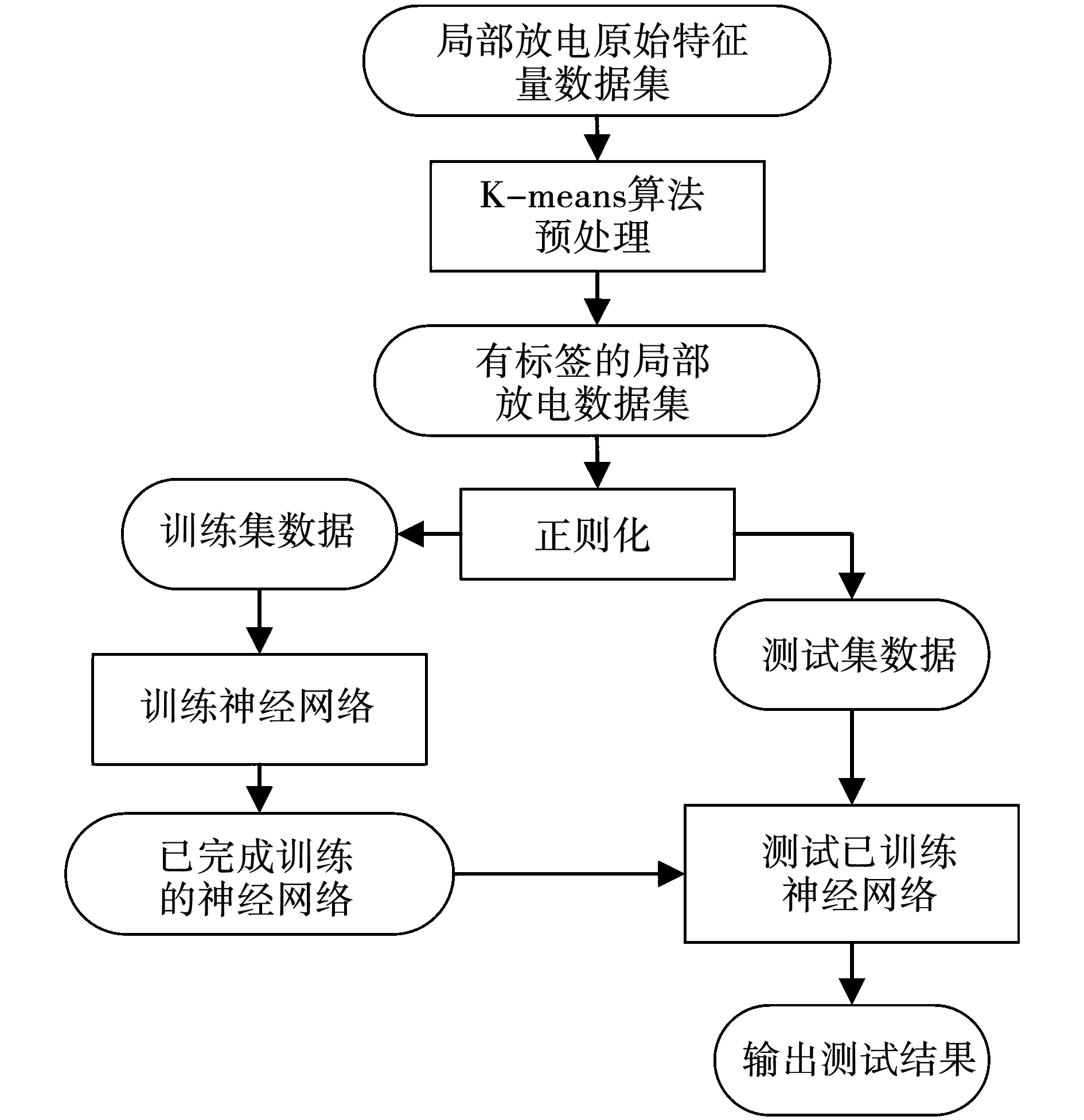
图7 神经网络的训练测试流程图Fig.7 Flow chart of neural network training and testing

适合的优化算法会使神经网络在运行过程中损失函数做到快速减少，达到较高的识别精度。为对比优化算法对运行效果影响，在使用64-32-32-16(数字代表每层隐含层的神经元数量)的4层结构作为神经网络结构(经初步测试该结构的拟合度较高、不易出现欠拟合或过拟合)、控制神经网络其他参数不变、暂定学习率为0.01的情况下，对神经网络在使用梯度下降法、RMSProp算法与Adam算法情况下损失函数的下降情况和训练集识别精度进行了对比，不同优化算法下损失函数曲线如图8所示。可以看出，相比于梯度下降法，Adam算法收敛效果较好，且不像梯度下降法那样易走向局部最优。同时Adam算法的收敛表现也不像RMSProp算法那样表现出较大程度的振荡并最终难以收敛。运用Adam算法后损失函数在大约750次迭代后趋于稳定。不同优化算法的训练集精度随迭代次数的变化曲线如图9所示。可以看出Adam算法具备高识别精度的优势，且不像RMSProp算法那样随着迭代次数增加而精度出现振荡现象，Adam算法不仅收敛速度快而且在收敛过程中精度一直处于稳定的状态。

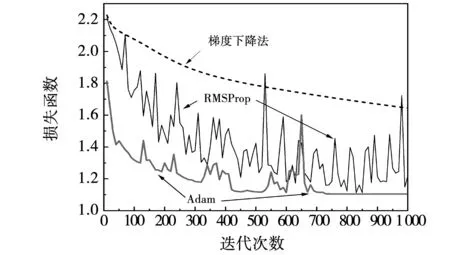
图8 3种优化算法的损失函数变化Fig.8 Changes in the loss function of the three optimization algorithms

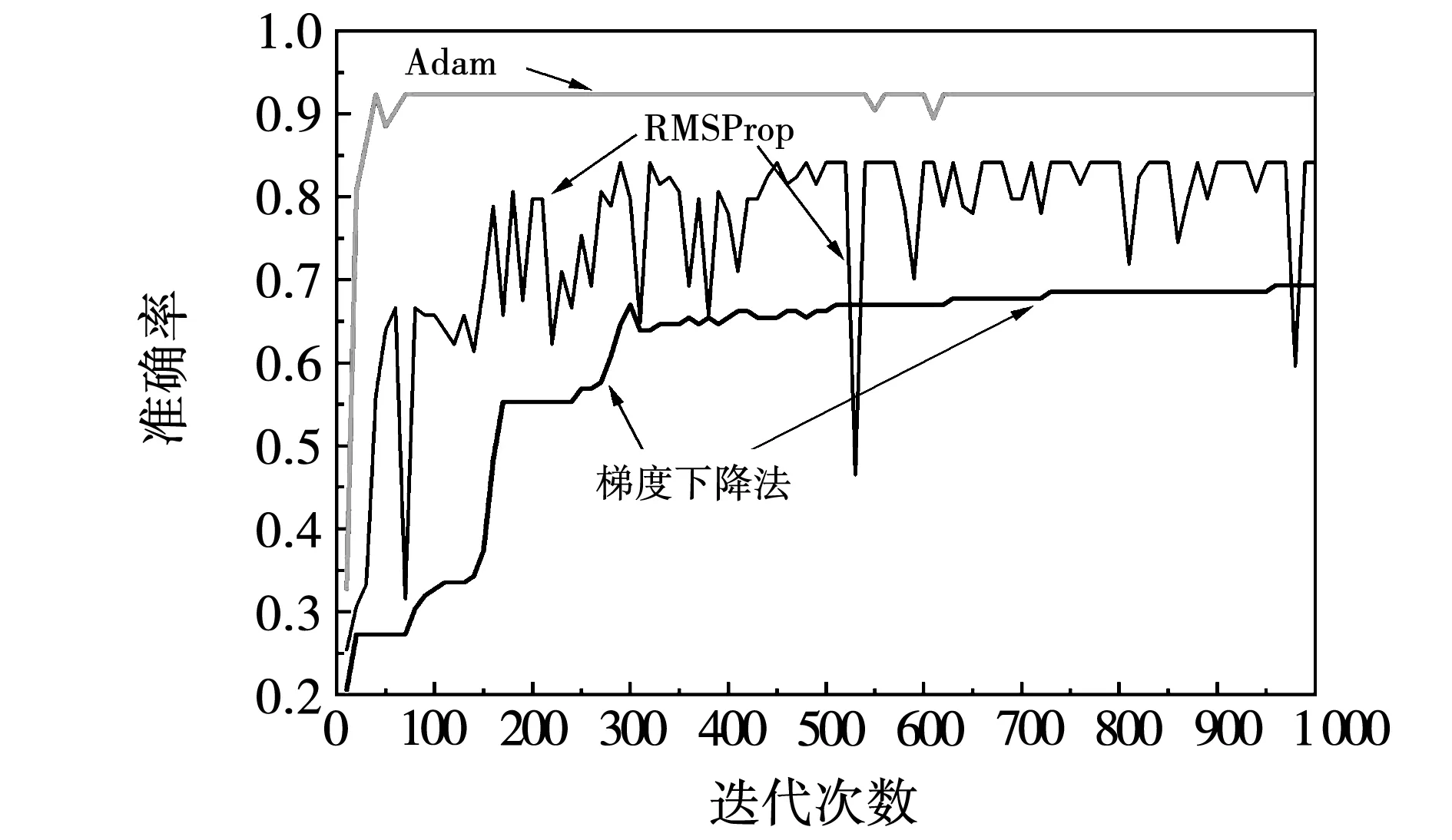
图9 3种优化算法下训练集精度变化曲线Fig.9 Variation curve of training set accuracy under different optimization algorithms

学习率会影响神经网络的误差优化算法的表现，因此这里对不同神经网络的学习率进行参数寻优，对比在学习率为0.1、0.01、0.001、0.000 1的情况下优化算法的表现，以使神经网络获取更好的训练集的学习和测试集的识别效果。控制神经网络其他参数不变，神经网络结构采用64-32-32-16的4层结构的，优化算法采用上述已优选的Adam算法，不同学习率的损失函数变化曲线如图10所示。可以看出，当学习率为0.1时，损失函数几乎不变，而当学习率为0.000 1时，损失函数曲线则是一条下降的曲线，直到1 000次迭代后仍是发散状态。这说明学习率过高，步长过大，使得函数无法做到收敛；学习率过低，步长过小，使得计算量极大，损失函数收敛速度极慢，由此说明应设定一个适中的学习率以兼顾收敛性与收敛速度，对比学习率为0.01与0.001时的收敛性与收敛速度，可以看出后者的收敛性与收敛速度更优，因此最终将学习率设定为0.001。

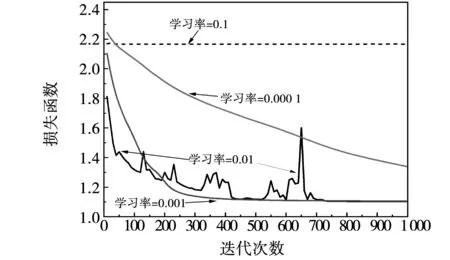
图10 3种学习率的损失函数变化Fig.10 Changes in the loss function of the three learning rates

神经网络的深度是神经网络参数中一个很重要的参数，神经网络的深度由隐含层的层数来表征，其在很大程度上影响该神经网络的非线性模拟能力与特征学习能力。控制神经网络其他参数不变，选择前文已优选的Adam算法和0.001为损失函数的优化算法与学习率，以此选取合适的深度。共对比3种隐含层结构的神经网络，如表3所示，其中64-32-32-16表示共有4个隐含层，其神经元数量依次为64、32、32、16，其他结构同理。

表3 用于对比的隐含层结构

这3种隐含层结构之所以选择64、32、16的组合是因为输入的特征量为16个，在此基础上成倍数选择神经元。经过初步测试后，在表3所示的这3种隐含层结构的拟合度最高，未出现欠拟合或者过拟合，由此选择这3种结构进行比较。不同隐含层数下的损失函数曲线如图11所示。可以看出Group 2为相对最优选择，其既不使损失函数下降速率相对过慢，且在达到相似效果的前提下(Group 2与Group 3曲线高度重合)具有较Group 3更为简单的结构，网络的结构过深、过复杂的网络结构会使网络的运行陷入梯度消失现象或梯度爆炸现象，由此采用Group 2的结构作为神经网络的隐含层结构。

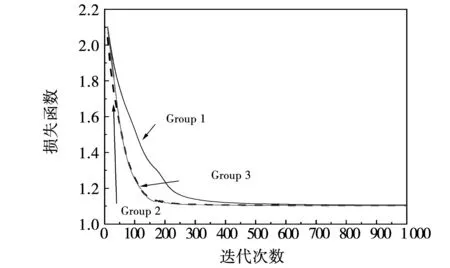
图11 3种隐含层的损失函数变化Fig.11 Changes in the loss function of the three type of hidden layers

根据上述结果建立了被优化的深层神经网络，其神经元为三阶神经元；隐含层结构为Group 2：64-32-32-32-16；损失函数优化方案选择为Adam算法+0.001的学习率。依据图7所述的流程对优化的深层神经网络进行训练与测试，并与相同条件下的使用KNN、SVM和BP神经网络的结果进行对比，其结果以混淆矩阵的形式呈现，如图12所示。可以看出，优化后的深层神经网络的表现优于其他三者的表现，前者的整体正确识别率已超过90%。

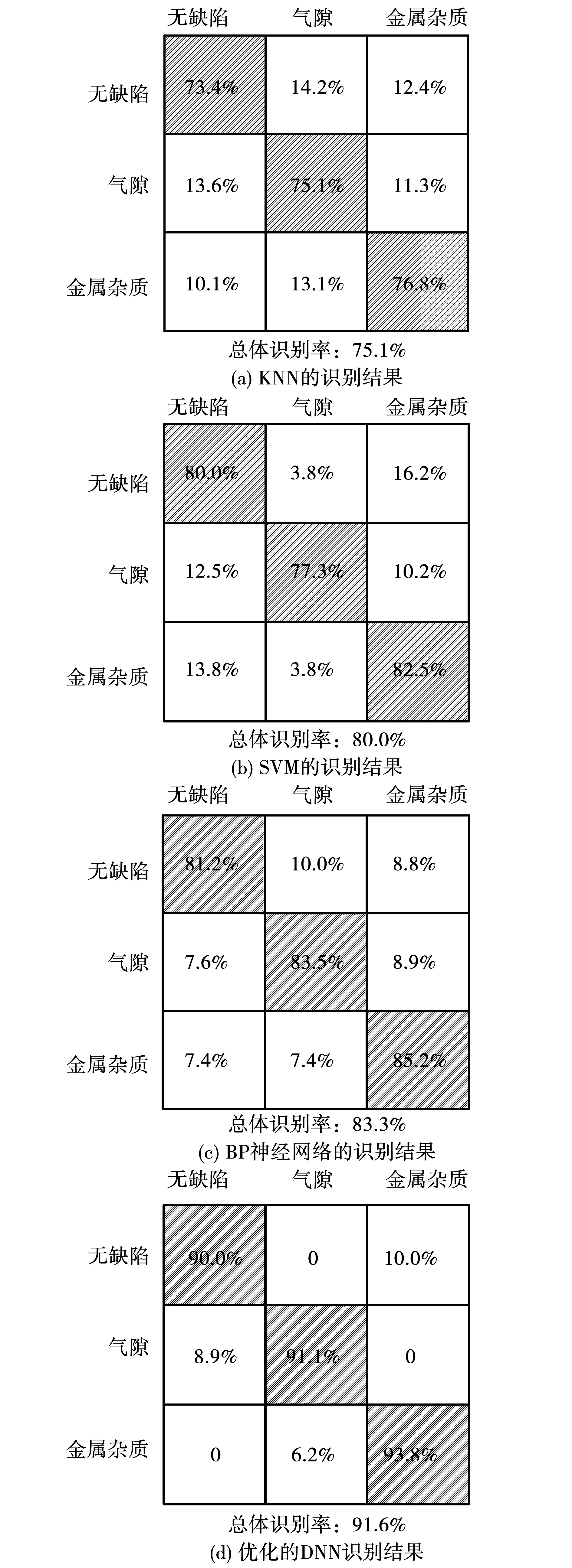
图12 不同方法的识别结果的混淆矩阵Fig.12 Confusion matrix of classification results with different methods

以上结果可以看出，采用深层神经网络+三阶神经元的结构处理局放特征量的方式，对无缺陷、含气隙缺陷以及含金属杂质缺陷的绝缘纸试样识别率可以达到91.6%以上，能够有效识别纸质绝缘件含缺陷导致的故障。在实际运用中，含气隙缺陷和金属杂质缺陷为主要的缺陷类型，因此该方法便于对变压器纸质绝缘件缺陷导致故障的快速处理。当局放超标，对局放特征分析结果为绝缘件含气隙或金属杂质时，可将筛查目标首先定位为纸质绝缘件，采用X光重点检查；分类结果为无缺陷时，应检查绝缘件是否有变形或安装不到位导致的油中放电。

3 结 论

1)运用Adam算法使损失函数能迅速下降并收敛，识别准确率相对最佳;当学习率设置为0.001时,使用Adam损失函数能迅速下降并收敛；当深层神经网络隐含层结构为64-32-32-32-16时，神经网络性能达到最优且未出现过拟合。

2)采用深层神经网络+三阶神经元的结构处理局放特征量的方式，对无缺陷、含气隙缺陷以及含金属杂质缺陷的绝缘纸试样识别率可以达到91.6%，优于传统KNN、SVM和BP神经网络的表现，进而能够有效识别纸质绝缘件含缺陷导致的故障，便于对变压器纸质绝缘件缺陷导致故障的快速处理。