开绕组永磁同步电机零矢量注入模型预测控制

冯智煜， 高琳， 殷凯轩， 付文华

(西安交通大学 电气工程学院，陕西 西安 710049)

0 引 言

永磁同步电机功率密度高，运行可靠，高效且控制简单，被广泛应用于工业领域中，成为伺服系统执行电机的首选[1-3]。但随着电动汽车、高铁以及工业产业链的发展，出于对其安全性及效率等方面的考虑，永磁同步电机的驱动系统中需要使用电压等级更低的直流电源，因此对提升电机驱动系统中直流母线电压的利用率提出了更高的要求，也成为目前永磁同步电机一个很重要的研究方向。

近年来，开绕组永磁同步电机(open-winding permanent magnet synchronous motor，OW-PMSM)受到广泛关注[4-7]，这种电机供电系统的拓扑结构是将星形连接的三相定子绕组的中性点打开，在定子绕组的首端和末端分别接入供电逆变器，同时采用两组逆变器对电机进行驱动控制。开绕组永磁同步电机在保持电机本身基本电磁结构不变的情况下，通过采用SVPWM调制中的多极开关组合，打破了传统星接电机驱动系统中SVPWM调制对直流母线电压利用率的提升极限，理论上可以提升到2倍，并能够提高逆变器的容错能力[8-11]。按照不同的供电方式，开绕组永磁同步电机的供电拓扑结构可分为隔离母线型和共母线型两种。隔离母线型拓扑结构采用两个独立的直流电源分别为两组逆变器供电，而共母线型拓扑结构是采用一个直流电源同时为两组逆变器供电，所以相比而言，共母线型拓扑结构的供电系统具有更小的驱动系统成本和体积。星接绕组永磁同步电机在采用SVPWM调制方法控制时，由于受星接结构制约，逆变器输出的零序电压不会产生零序电流。隔离母线型拓扑结构由于也不存在零序电流回路，因此也避免了零序电流的产生，同时两侧供电直流电源可选用大小不同的电压，在相绕组上产生更多电平等级，所以灵活性更好[12]。而在共母线型拓扑结构中，采用的共母线为零序电流提供了通路，零序电流的存在不仅占用逆变器容量，而且还会引起电机转矩的脉动，因此针对共母线型拓扑结构中零序电流的抑制已成为开绕组永磁同步电机的研究热点[13-15]。

在共母线型拓扑结构的开绕组永磁同步电机中，逆变器输出的零序电压会产生零序电流，同时定子绕组中的三次谐波反电势也会产生零序电流。电机内部永磁磁链的三次谐波分量在定子绕组中感应产生三次谐波反电势，进而产生三次谐波电流，也就是零序电流。为了抑制零序电流，文献[16]提出了电压矢量的中六边形调制方法，使两组逆变器在不同开关组合内均产生大小相等,同相位的零序电压，它们相互抵消，因此逆变器组的输出电压中不含零序分量。同时这种方法选取的电压矢量位于电压矢量图的中六边形上，是传统SVPWM调制采用的正六边形电压矢量的1.7倍，因此可将直流电源的电压利用率提高1.7倍。文献[17]通过提高逆变器开关频率并采用补偿装置来抑制逆变器产生的零序电压，从而减小零序电流。文献[18]在控制系统中将永磁磁链产生的三次谐波反电势考虑在内，增加对零序回路的控制，利用比例谐振(PR)控制器，对回路内指定频率的零序分量进行抑制，使逆变器输出的零序电压与电机内部的三次谐波反电势相抵消。但这种方法采用的是SPWM调制，丢失了SVPWM调制所具有的直流母线电压利用率高的优点。文献[19]提出了一种重新分配零矢量作用时间产生指定零序电压的方法，即带零序电压输出的SVPWM技术，将三次谐波反电势考虑在内，配合控制环，对回路零序电流进行抑制。为降低零序电流对转矩脉动的影响，文献[20]提出了一种q轴电流注入法，在q轴电流中注入与零序电流产生转矩脉动相当的六倍频电流分量，直接抵消零序电流产生的转矩波动，提高电机运行性能。

模型预测控制由于其控制系统结构简单，滚动优化响应性能好等优势，逐渐被引入到开绕组永磁同步电机控制系统中。文献[21]针对开绕组电机，在传统模型预测的控制策略中引入一种含零序电流的价值函数，对0轴电流进行跟踪，进而选取出最优开关电压矢量，但这种方法对零序电流的抑制效果有限。

文献[22]提出一种混合双矢量的控制策略，能同时抑制逆变器和电机三次谐波反电势产生的零序电流。逆变器的输入采用不产生零序电压的开关矢量与零矢量组合的调制信号，通过零矢量在其中一个逆变器上的混合调制，对电机三次谐波反电势进行抑制。该调制方法能够有效地抑制零序电流，但其调制方法对d轴电流的控制效果不佳，d轴电流脉动大，影响电枢电流及电磁转矩的稳定性。且直流母线电压利用率等同于中六边形调制方法，仅提升至传统SVPWM调制的1.7倍，没有达到理论上的2倍，并受零序电压控制的影响。文献[23]提出一种基于开绕组结构的四桥臂变换器驱动系统的新型拓扑结构，但其控制方法与中六边形调制法类似，并未将电机永磁磁链产生的三次谐波反电势考虑在内，不能对零序电流产生完全抑制的控制效果。

为了有效地抑制回路零序电流，并最大限度地提升直流母线电压的利用率，本文针对共母线型拓扑结构的开绕组永磁同步电机提出一种改进的模型预测控制策略。根据电机预测模型得到αβ0坐标系下的期望电压，设计一种电压误差代价函数，按照电压误差最小化原则选取出最优电压矢量及其最优作用时间，并计算出所需补偿的零序电压大小。采用零电压矢量注入方式对控制系统进行补偿，并计算出零序电压的补偿限度，在预测模型中对其进行限幅。仿真计算表明，本文提出的方法能够有效地抑制开绕组电机中的零序电流，并将直流母线电压的利用率提高到传统SVPWM调制的2倍，达到理论最大值。该方法中的最优电压矢量从基本电压矢量中选取，无需矢量合成，因此调制方法更简单，而且最优电压矢量的占空比采用一定精度的刻度选取，刻度大小的选择可根据用户处理器能力以及对目标控制精度的要求灵活选取。

1 传统模型预测控制

1.1 OW-PMSM数学模型

图1所示为共母线OW-PMSM的驱动系统原理图，两组逆变器由同一个直流电源供电，可见这样的拓扑结构为零序电流流通提供了回路。

图1 共母线OW-PMSM驱动系统原理图Fig.1 Schematic diagram of OW-PMSM drive system with common DC bus

开绕组PMSM在abc坐标系下的定子电压方程可表示为

(1)

式中：ua、ub、uc分别为定子三相电压；ia、ib、ic分别为定子三相电流；ψa、ψb、ψc分别为定子三相磁链；Rs为绕组每相电阻。

如图1所示，由于零序电流回路的存在，定子绕组匝链的转子永磁磁链的三次谐波分量需被考虑，因此OW-PMSM磁链方程可表示为

(2)

式中：Laa、Lbb、Lcc分别为三相绕组自感；Lab、Lac、Lba、Lbc、Lca、Lcb分别为abc三相绕组间互感；ψf为定子绕组匝链的永磁体磁链的幅值；ψ3f为匝链的永磁体磁链三次谐波分量幅值，θ为电机转子d轴与a相绕组之间的电角度。

经过坐标变换，OW-PMSM在dq0坐标系下的数学模型为

(3)

式中：ud、uq、u0分别为定子dq0轴电压；id、iq、i0分别为定子dq0轴电流；Ld、Lq、L0为定子dq0轴电感；Rs为定子每相电阻；ωe为转子电角速度。

1.2 OW-PMSM驱动系统电压矢量

共母线OW-PMSM的驱动系统具有双逆变器结构，两组逆变器共同作用于电机，如图1所示。图2为两组逆变器电压矢量图，每个逆变器的输出同传统SVPWM的空间矢量图，可产生23=8个电压矢量。对于开绕组电机，作用在其定子绕组上的电压矢量是由两组逆变器产生的合成电压矢量，即

uαβ=uαβ-1-uαβ-2。

(4)

式中：uαβ为在αβ坐标系中作用在开绕组电机定子上的电压矢量；uαβ-1和uαβ-2分别为图2所示单一逆变器电压矢量图。因此，开绕组电机驱动系统具有26=64种开关组合，能够在空间上合成更多的电压矢量，从而产生类似三电平逆变器的控制效果。图3为双逆变器合成电压矢量图，一共有19种不同的电压矢量空间分布(分别用A-S表示)。

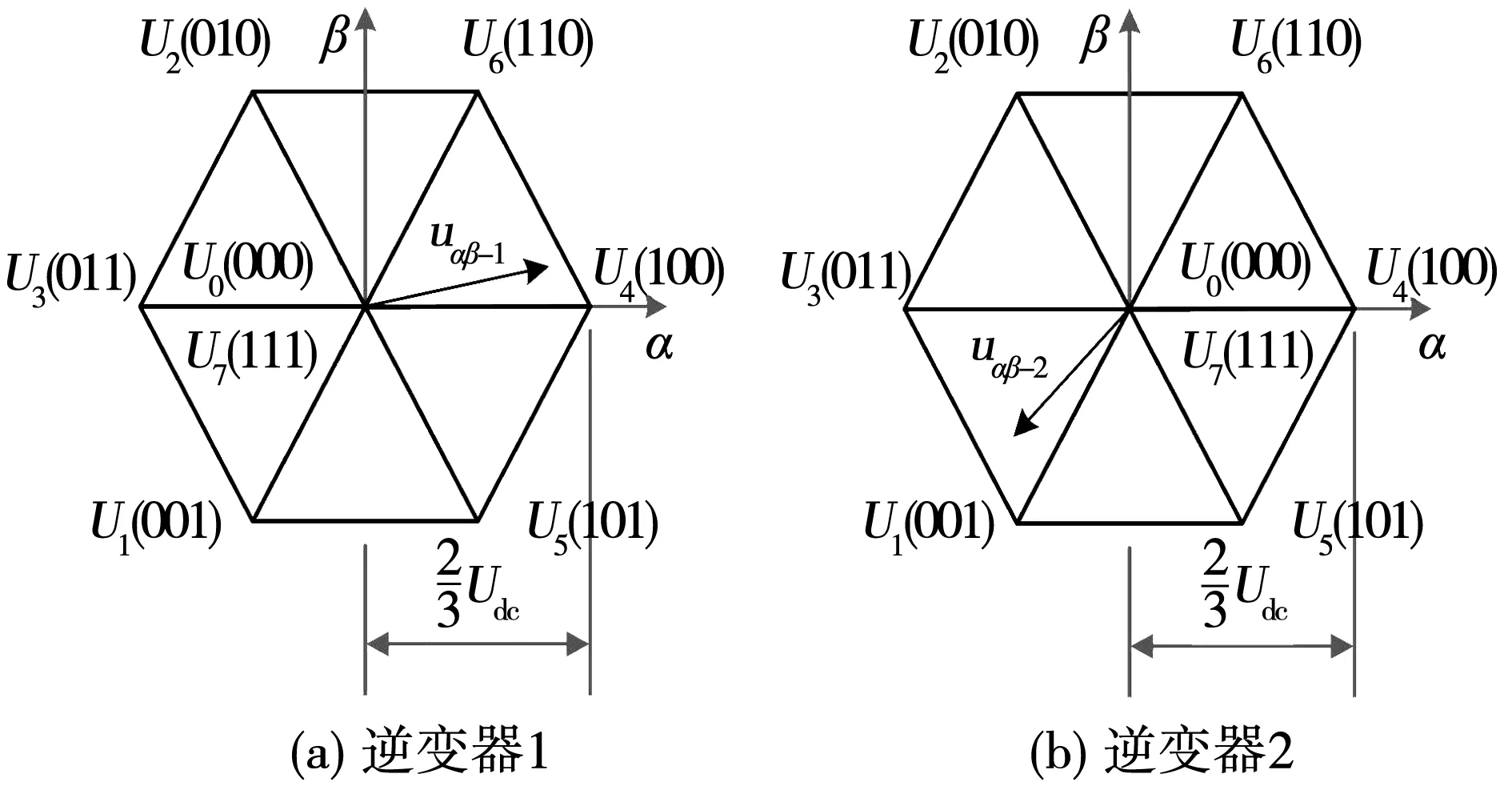
图2 两组逆变器电压矢量图Fig.2 Voltage vector of each inverter

图3 双逆变器电压合成矢量图Fig.3 Voltage vector distribution of dual inverters

双逆变器在产生不同电压合成矢量的同时，各个开关组合形成的零序电压矢量大小也不相同，两组逆变器会分别产生幅值为0、1/3Udc、2/3Udc和Udc的零序电压，其差值为作用在开绕组电机上的零序电压幅值，即

u0=u0-1-u0-2。

(5)

式中：u0为开绕组电机定子上的零序电压矢量；u0-1和u0-2分别为逆变器1和逆变器2产生的零序电压矢量，因此能产生7种不同幅值的合成零序电压矢量，即-Udc、-2/3Udc、-1/3Udc、0、1/3Udc、2/3Udc和Udc。图3中各节点所产生的零序电压大小如表1所示，其中括号内的两位数为双逆变器所产生的64种开关组合，第一位的0-7表示逆变器1的8种开关状态，分别为000、001、010、011、100、101、110、111，第二位的0-7表示逆变器2的8种开关状态，例如K点的开关组合(12)表示逆变器1的开关状态为1(001)，逆变器2的开关状态为2(010)。

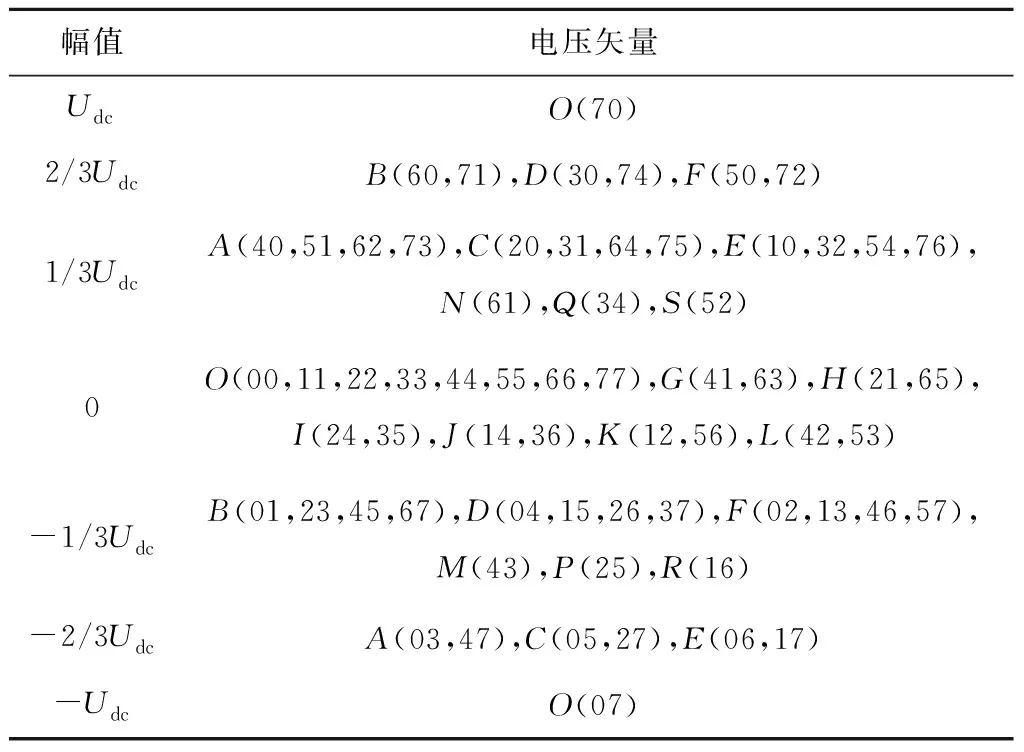
表1 双逆变器合成电压矢量中的零序电压幅值

1.3 共母线OW-PMSM系统的传统模型预测控制

传统模型预测控制方法通过预测模型及代价函数，来选择出作用于电机的最优电压矢量及开关组合。首先分析OW-PMSM系统的预测模型，并选取相应的价值函数。对式(3)电压方程利用前向欧拉法展开，得到开绕组电机控制系统的流预测模型

idq0(k+1)=Aidq0(k)+Budq0(k)+H。

(6)

式中：

其中e0为电机反电势的三次谐波分量，其大小关系满足e0=3ωeψ3fsin3θ。

传统模型预测电流控制(model predict current control，MPCC)方法主要实现对给定电流的跟踪，即给定idref、iqref和i0ref，在价值函数中引入电流项，表示为

g=|idref-id|+|iqref-iq|+λ|i0ref-i0|。

(7)

当λ=0时，式(7)所示的价值函数就是星接PMSM系统MPCC的代价函数。

对于开绕组PMSM系统，由式(3)可得零序通路的电压方程

(8)

可见，由于零序回路中的零序电感L0较小，若存在零序电压将会产生较大的零序电流，而传统MPCC在一个开关周期内仅有一个电压矢量起作用，控制系统精确度差，因此，传统MPCC存在较严重的零序电流问题。

由此，基于式(7)价值函数在27种控制电压矢量中可选取下一控制周期内的最优电压矢ubest。

2 改进的零矢量注入模型预测控制

本文针对共母线OW-PMSM系统提出一种改进的模型预测控制方法，该方法基于混合矢量法，将αβ0轴上的电压矢量分为两步进行控制，达到对零序电压的完全抑制。第一步先对由系统无差拍预测模型所得到的参考电压矢量进行跟踪，第二步则根据所选取的电压矢量及其在单个开关周期内的作用时间，计算得到所需补偿的零电压矢量，并在开关周期内对其进行混合。最终，对零序回路中的零序电压完全抑制，并在最后对零序电压的抑制限度进行分析。

2.1 参考电压的模型预测跟踪

不同于常规模型预测电流控制MPCC对轴系中全部27种电压矢量组合进行选取，也不同于文献[22]中仅选取不产生零序电压的中六边形混合矢量调制，在本文所提改进后的模型控制中，为在不增加计算负荷的同时，最大限度提升直流母线利用率，选取电压矢量图中外侧12种电压矢量于价值函数内进行筛选，即GHIJKLMNPQRS两六边形。

同时，为了更好地跟踪所需电压矢量，引用无差拍模型预测控制理论，定义转速环的输出为iqref，采用的id=0控制方法，设定idref为0，为后续抑制零序电流，亦设i0ref为0，并将其代入到式(6)开绕组电机系统的电流预测模型中，即令

(9)

根据式(6)，将式(9)代入得

(10)

式中：

再经过坐标变换，将同步旋转坐标系dq轴下的参考电压udqref转换到两相静止坐标系内得到uαβref，方便后续控制过程中利用价值函数进行比较筛选。

在本文所提控制方法的第一步中，仅需实现对αβ轴参考电压uαβref的跟踪，后续0轴电压则采用零电压矢量的注入来进行补偿控制，因此设定第一步筛选时的价值函数为

g=|uα(k+1)-uαref|+|uβ(k+1)-uβref|。

(11)

由上节分析知，在图3中最外侧电压矢量共有12个，根据式(11)所示价值函数进行最优比较后，可选取得到最优矢量Vi，此次比较筛选为第一次筛选，旨在选取得到最优矢量角度并作为后续选取最优矢量模。

在选取得到Vi之后，需经历第二次筛选得到其在一个开关周期内的最优作用时间占比n，建立一定取值间隔的时间占比数组ni=0,…,1，将其作为电压矢量的作用时间占比构建一系列的电压矢量V(ni)，如图4所示。在这些电压矢量中进行第二次最优筛选：

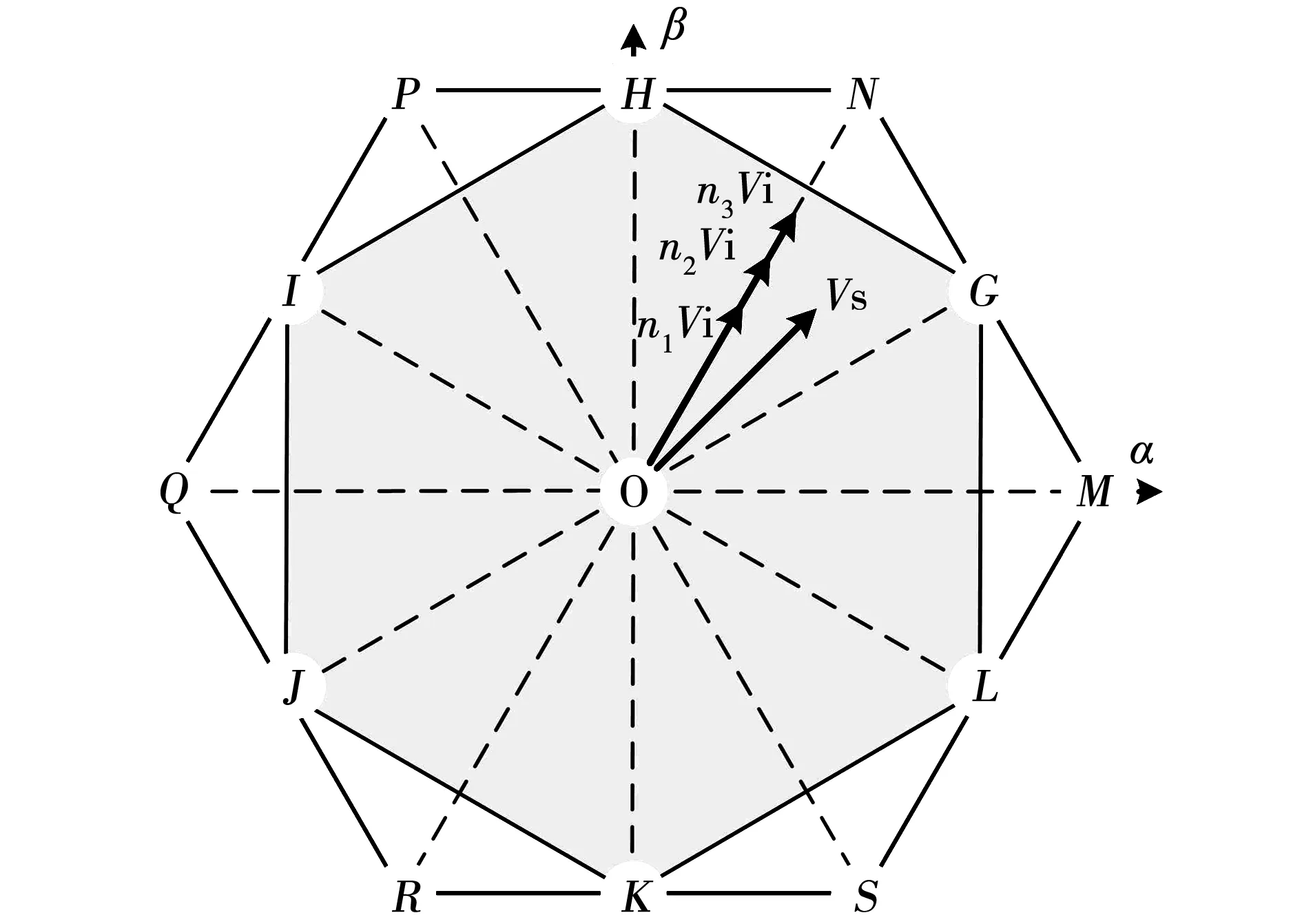
图4 αβ平面电压矢量调制Fig.4 Voltage vector modulation of the αβ subspace

V(ni)=niVi,ni⊆(0,1)。

(12)

考虑到计算负荷和控制效果，应该适当选取参数n的取值间隔Δn，当取值间隔选取过大，将会导致最优作用时间占比选取精确度不足，系统响应慢，控制效果不好；而当取值间隔过小，虽然控制精确度高，但会导致计算负荷大。具体取值间隔大小的选取可根据用户处理器运行能力选取，用户可根据自身处理器能力以及对目标控制精度自我把握平衡评估次数。本文为确保结果不失一般性，设定取值间隔Δn=0.1，此时ni=0,0.1,0.2,…,1，共11个电压矢量，在其中选取最优非零电压矢量。选取此取值间隔，既达到了一定的控制精确度，也减轻了系统负担，系统响应快。

利用相同的价值函数即式(11)筛选得到一个开关周期内的最优矢量作用时间n，以此得到最优电压矢量V(n)，最终再与第二步控制中注入的零矢量进行混合调制。

2.2 零序电压抑制补偿

考虑到电机自身永磁磁链3次谐波的存在，其反电势中存在零序电压分量，仅由中六边形调制法不能完全消去零序回路中的零序电流，在式(10)中，得到0轴参考电压u0ref，若能使逆变器0轴电压输出跟踪其参考电压，则回路内零序电压便可以被完全补偿。

当第一步所得的电压矢量V(n)确定后，通过计算，可以得出其产生的零序电压大小，记为u10，由于电机运行状况不定，这一零序电压大小必定与所需的参考电压u0ref之间存在差值，若需补偿这一部分差值，需要产生对应差值大小的零序电压，且对前面所得到的αβ轴电压矢量不产生影响，在图3中，零电压矢量(O点)既不影响αβ轴电压矢量，又存在正负零三种大小的零序电压，故可通过注入不同开关组合产生的零电压矢量来补偿所需零序电压，于本文中称为零矢量注入法，零轴电压参考矢量u0ref和第一步筛选所得到的电压矢量u10共同决定所需注入的零序参考电压，即所需注入的零序电压为u20满足以下等式：

u20=u0ref-u10。

(13)

式中，u20的符号不定，可为正亦可为负，当u20为正时，需要能够产生正零序电压的零电压矢量进行补偿，其开关组合为70(111000)，此开关组合能够产生幅值大小为Udc的零序电压，将其注入前面的到的电压矢量V(n)中即可得到所需电压矢量；同理，当u20为负时，则需要能够产生零序电压大小为-Udc的开关组合07(000111)进行补偿并注入。通过计算得到注入零矢量作用时间占比a后，注入V(n)中即可得到最终参考电压矢量。由于70和07产生的零序电压幅值相同，均为Udc，因此零矢量作用时间占比a的表达式可以进行合并统一，计算得到，补偿的零电压矢量作用时间占比为

(14)

因此，最终得到的电压矢量为

V′(n)=nVi+aV0。

(15)

其中V0为70或者07，剩下的开关周期用00或11补齐。

2.3 零序电压补偿限度

注意到零序电压的补偿需要特定的零电压矢量占用开关周期时间，可见在产生所需电流的非零电压矢量占用大部分开关周期后，零序电压的抑制也受限，下面分析其受限区间。

当第一步筛选得到电压矢量V(n)后，所占用的开关时间为nTS，则零电压矢量补偿时间最大为(1-n)TS，又由于零电压矢量产生的零序电压大小为Udc或者-Udc，则0轴参考电压的限幅为

u0ref⊆(-(1-n)Udc+u10,(1-n)Udc+u10)。

(16)

当u0ref超过限幅时，u0ref的取值应限制在式(16)所示区间内。

2.4 改进后模型预测控制整体方法

图5所示为改进后模型预测控制框图，首先，利用无差拍电流预测的原理，转速环PI调节器输出得到q轴电流的参考值iqref，本文仿真电机选用表贴式开绕组永磁同步电机，控制方法是基于id=0控制，为实现对零序电流的抑制作用，0轴电流参考值为0，由当前时刻电机运行状态通过电流预测可得参考电压udq0ref。经过坐标变换得到αβ轴参考电压后，通过先后两次价值函数的筛选得到基础电压矢量及其占比；然后根据所选电压矢量及0轴参考电压计算得到所需补偿零电压矢量及其作用时间，并对其进行限幅，最后对电压矢量进行零矢量注入，得到最终电压矢量V′(n)，并将其作用于逆变器组。由此，本文所提出改进型模型预测控制的两步调制完成。

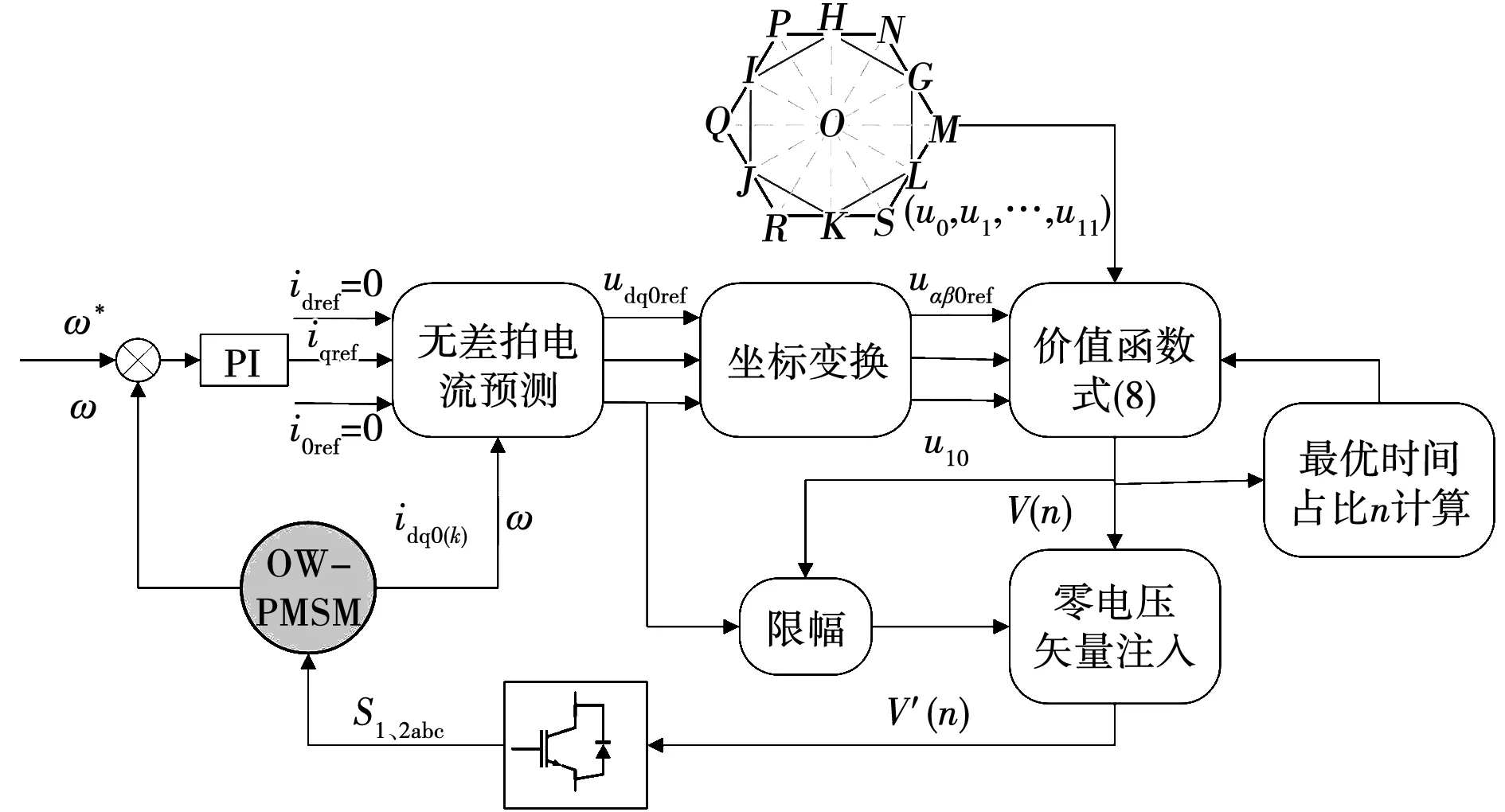
图5 改进后模型预测控制框图Fig.5 Improved model predictive control scheme

3 仿真验证及分析

在MATLAB/Simulink环境中搭建id=0控制策略下的开绕组永磁同步电机模型预测控制模型。电机参数见表1，控制周期T=100 μs。

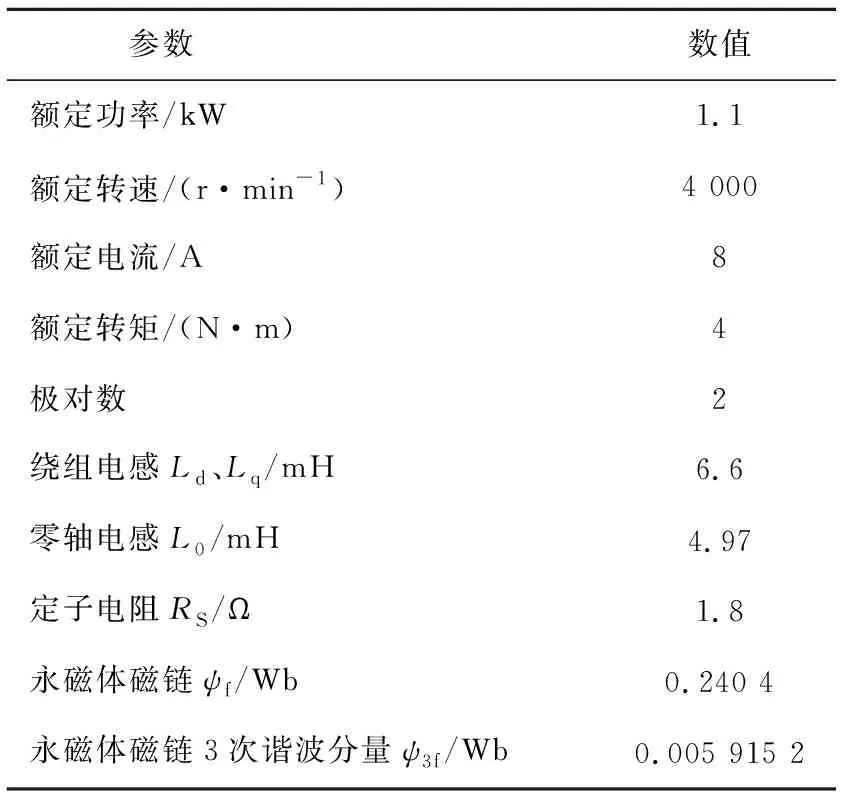
表2 仿真模型的参数[22]

3.1 零序电流抑制仿真验证

为了验证本文所提方法的有效性，对电机在不同工况下运行，速度环采用传统的PI控制器，相对于传统MPCC控制，对比改进后的模型预测控制与其的稳态性能。在三种不同转速运转情况(即低速1 000 r/min、中速2 000 r/min、额定速度4 000 r/min)下进行仿真。图6～图8为在额定负载4 N·m下的仿真运行情况对比。在低速1 000 r/min工况运行时，电机在0 s空载启动，并在0.1 s加额定负载，由图6(a)和图6(b)可见，相比于传统MPCC，改进后的模型预测控制的稳态运行情况大大改善，首先零序电流的电流脉动Δi0基本消去，同时dq轴电流脉动明显减小，电枢电流总谐波畸变率THD从35.47%降至10.82%。

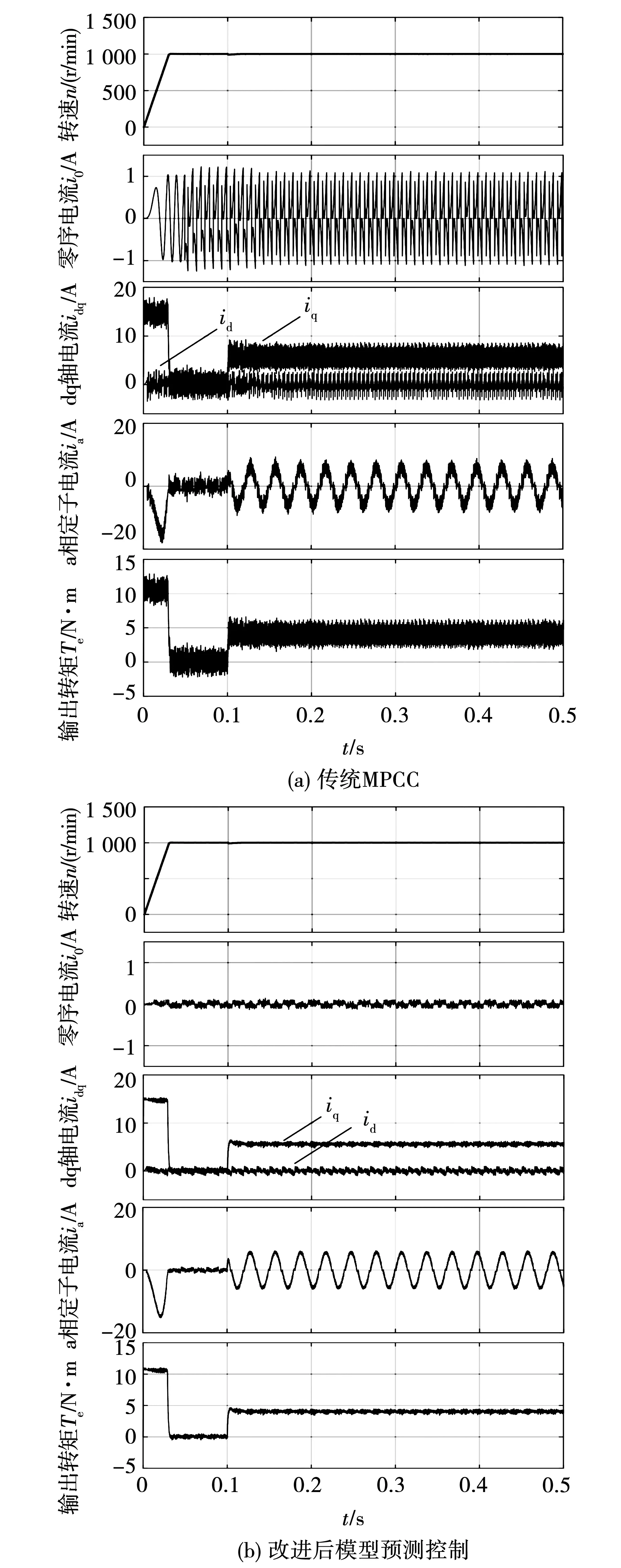
图6 两种方法在低速工况1 000 r/min下的仿真对比Fig.6 Simulation results of two methods at low speed of 1 000 r/min

在中速2 000 r/min工况运行时，同样，电机在0 s空载启动，并在0.1 s加额定负载，对比图7(a)和图7(b)可见，相比于传统MPCC，稳态运行情况亦大大改善，零序电流的电流脉动Δi0从1.3 A降低并基本消去，同时dq轴电流脉动明显减小，电枢电流总谐波畸变率THD从35.85%降至10.03%。

图7 两种方法在中速工况2 000 r/min下的仿真对比Fig.7 Simulation results of two methods at medium speed of 2 000 r/min

而在额定转速4 000 r/min工况运行时，电机在0 s空载启动，并在0.25 s加额定负载，对比图8(a)和图8(b)可见，相比于传统MPCC，稳态运行情况亦大大改善，零序电流的电流脉动Δi0从4 A降至1.8 A，同时dq轴电流脉动明显减小，电枢电流总总谐波畸变率THD从36.89%降至12.78%。

图8 两种方法在额定工况4 000 r/min下的仿真对比Fig.8 Simulation results of two methods at rated speed of 4 000 r/min

3.2 直流母线利用率提升仿真验证

为了验证本文所提方法在直流母线利用率提升方面的有效性，相对于中六边形调制法[16]，本文给出电机在同参数条件下两种方法的电机转速提升极限，整体控制方法基于id=0控制，负载转矩在额定负载4 N·m，以模拟电机在实际工况运转时转速在额定转速上的提升情况。

图9给出在额定负载转矩下，两种方法的转速提升极限情况，给定转速为6 400 r/min(此转速值大于中六边形调制法所能达到的理论转速极限)，由图9(a)和图9(b)对比可以看出，中六边形调制法不能达到给定转速，仅能将转速提升至6 150 r/min，而本文所提方法由于直流母线利用率的提升，可以达到普遍中六边形调制法所达不到的转速。可见，本文所提方法对直流母线利用率提升的有效性。

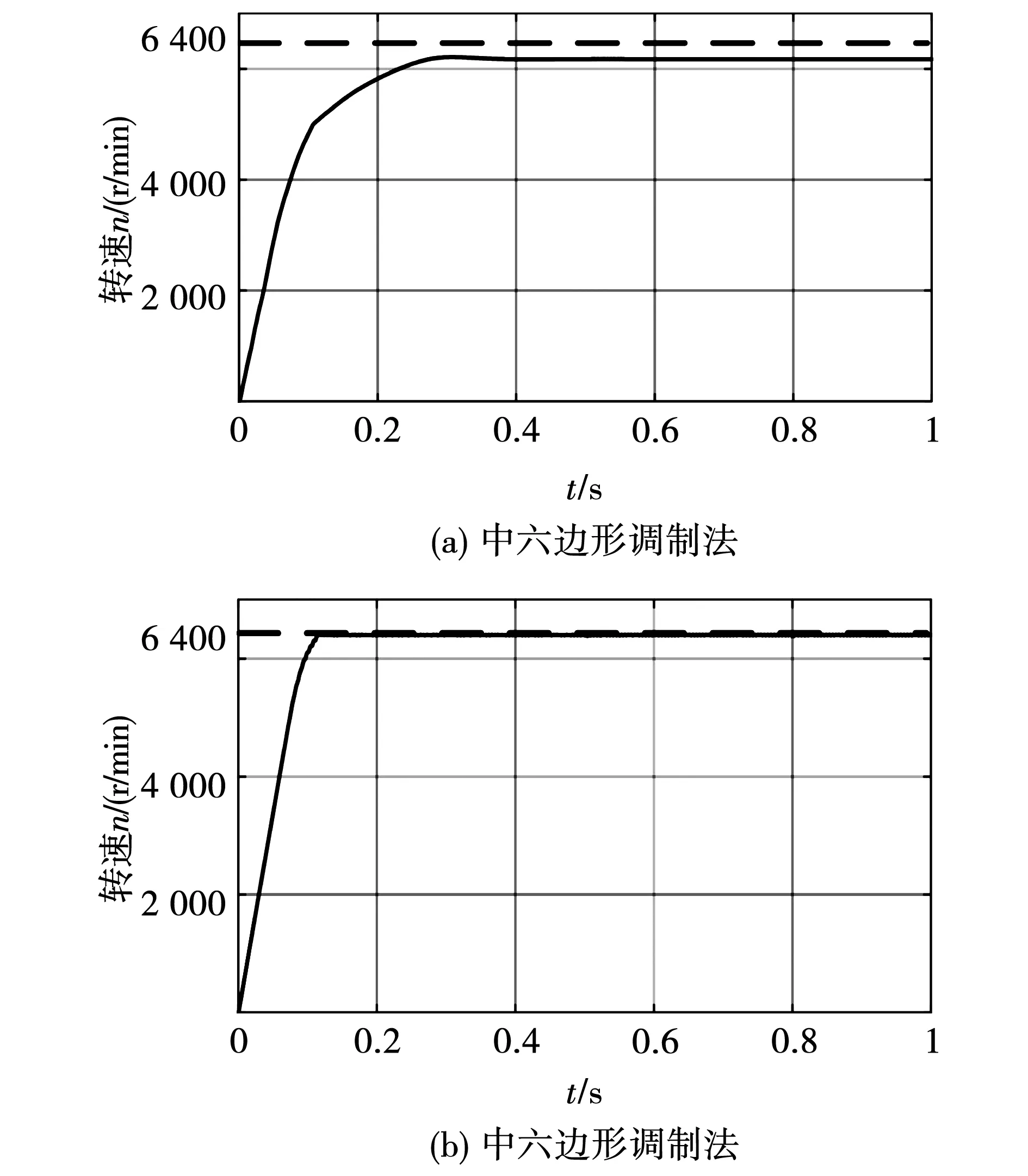
图9 两种方法在额定负载转矩4 N·m下转速提升 仿真结果对比Fig.9 Simulation results of two methods at speed increase with 4 N·m load

3.3 不同控制精确度控制器负担对比仿真验证

进一步对本文所提零矢量注入法的控制器负担进行分析，电机参数固定为同一准确参数值，电机空载启动。以上述仿真结果所设最优时间占比取值间隔Δn=0.1为参考，给出在不同取值间隔下的控制器负担及q轴电流脉动对比，如图10所示，其中控制器相对负担为同等环境下不同取值间隔与参考取值间隔控制时间的比值。

图10 不同取值间隔下的控制器负担及q轴电流 脉动对比Fig.10 Controller burden and q-axis current ripple at different value intervals

从图10知，取值间隔在0.1到1之间时，随着取值间隔的增大，控制器相对负担减小，q轴电流脉动增大，代表q轴电流控制精确度下降。综上，不同的最优时间占比取值间隔Δn将会影响系统控制精确度和控制器负担，更小的取值间隔带来更高的控制精确度，但对控制器的负担也会更大。

4 结 论

本文提出一种适用于共母线型开绕组永磁同步电机的改进模型预测控制方法，通过对无差拍预测电压跟踪以及对零序电流抑制的零电压矢量注入的两步调制方法，可以实现对零序电流的抑制以及dq轴电流的准确跟踪，相对于传统预测方法，有效的抑制了零序电流，具有更好的稳态性能，同时，相对于中六边形调制法，进一步提升了直流母线利用率。