基于功热转换机理修正SUS301L-MT不锈钢J-C本构模型

丁浩谞，朱 涛，肖守讷，王小瑞，阳光武，杨 冰

(西南交通大学牵引动力国家重点实验室，成都 610031)

0 引 言

不锈钢是轨道列车车体结构的常用材料之一，其中SUS301L不锈钢因具有良好的抗晶间腐蚀性和较高的强度而得到广泛应用[1-2]。轨道列车在碰撞过程中的冲击动能主要通过车钩缓冲装置、防爬吸能装置及车体端部等结构的塑性变形来吸收[3]。建立完整的材料动静态本构关系是准确模拟轨道列车吸能装置和车体端部结构塑性变形过程的首要前提[4]。

针对宏观角度构建的动态本构模型方面，工程中常采用表达形式简单、模型参数获取方便的Johnson-Cook(J-C)、Cowper-Symonds(C-S)等经典本构模型。然而，由于模型参数数量较少，对材料应变速率或温度等效应的表征能力有限，这些经典本构模型在应用于某些材料时的准确度较差。为此，研究人员针对不同材料对这些经典本构模型进行了修正。HUH等[5]对60TRIP钢和60C钢进行了准静态拉伸及霍普金森动态拉伸试验，并对J-C模型进行了修正，通过压溃管的试验与仿真验证了修正模型的有效性。杨晓康等[6]针对TC17钛合金在高温高应变速率条件下的不连续屈服现象，通过引入相关系数及平均相对误差对J-C模型进行了修正。汪振兴等[7]针对U75V钢在环境温度为500～700 ℃时具有的动态应变时效现象，引入临界温度与强化系数对J-C模型进行了修正。罗登等[8]针对Q1100钢的应力-应变曲线由动态回复型转变为动态再结晶型的现象利用多项式修正了J-C模型的温度项。

在从微观角度构建不锈钢动态本构关系方面，国内外学者主要对不锈钢的马氏体转变效应进行了研究。LU等[9]研究发现，低温时304不锈钢屈服强度提高而塑性下降的现象与低温下马氏体转变有关。李顺荣等[10]研究发现，应变增加使得304和316不锈钢中马氏体含量增加。王步美等[11]研究了室温下304不锈钢在准静态(0.000 5 s-1)和低应变速率(0.02 s-1)下的拉伸行为，发现在应变小于15%时准静态拉伸产生的马氏体量小于低应变速率时产生的马氏体量，而在应变大于15%时则相反。吴亮等[12]研究发现，马氏体沉淀硬化不锈钢FV520B具有典型的应变速率硬化效应与温度软化效应，且Power-Law模型比经典J-C模型更适用于描述该不锈钢的力学性能。这些研究大多定性地研究了不锈钢的微观机制，或仅定性地考虑了微观机制与宏观力学性能之间的联系。

综上所述，多数学者对不锈钢本构关系的研究主要集中在宏观唯象分析或微观定性分析上，针对不锈钢材料所建立的本构模型没有考虑不锈钢的马氏体相变过程和绝热温升的影响，所以本构模型对金属材料力学行为的描述精确度低。因此，作者对SUS301L-MT不锈钢进行了准静态及动态拉伸试验，获得了不同应变速率下的应力-应变曲线，并基于其功热转换机理对经典J-C本构模型进行了修正。

1 试验方法与结果

试验材料为国内某钢厂提供的SUS301L-MT不锈钢板，尺寸为500 mm×500 mm×3 mm，热处理工艺为1 050 ℃保温30 min水冷，其主要化学成分见表1，符合JIS G4305: 2005标准要求。SUS301L-MT不锈钢板的显微组织由原始奥氏体晶粒和板条马氏体构成[13]。按照GB/T 228-2002，在不锈钢板上截取片状准静态及动态拉伸试样，试样厚度均为1 mm，试样尺寸如图1所示。采用MTS809.25型材料试验机进行准静态拉伸试验，应变速率为0.000 5 s-1，采用位移控制，变形数据通过引伸计测试。采用ZWICKHTM5020型高速拉伸试验机进行动态拉伸试验，应变速率分别为0.1，1，10，100，500 s-1，拉伸速度通过试样标距段长度(12.5 mm)进行估算。动态拉伸试验前在动态拉伸试样表面喷涂白色底漆并喷洒均匀一致的黑色散斑点，使用数字图像相关法(DIC)测试应变，DIC测试标距段长度为8 mm。准静态及动态拉伸试验每组均重复3次，取平均值。

图1 准静态及动态拉伸试样尺寸

表1 SUS301L-MT 不锈钢板的化学成分

由图2可以看出：SUS301L-MT不锈钢在准静态拉伸过程中具有明显的应变硬化效应，流动应力-塑性应变曲线呈S形；SUS301L-MT不锈钢在动态拉伸过程中具有明显的应变速率强化效应，且随应变速率的增加，流动应力-塑性应变曲线逐渐趋于直线形，即试验钢的应变硬化效应随着应变速率的增加而减小。这是由于SUS301L-MT奥氏体不锈钢在准静态拉伸过程中，塑性变形至一定程度后发生马氏体相变，使其本构曲线斜率上升；而在动态拉伸过程中，塑性应变较小时快速拉伸不能及时诱发交滑移以及晶界滑移等塑性变形机制，使得马氏体相变量增加，而应变较大时产生的绝热温升抑制了马氏体相变，最终使得动态本构曲线斜率呈先增大而后减小的趋势[14]。

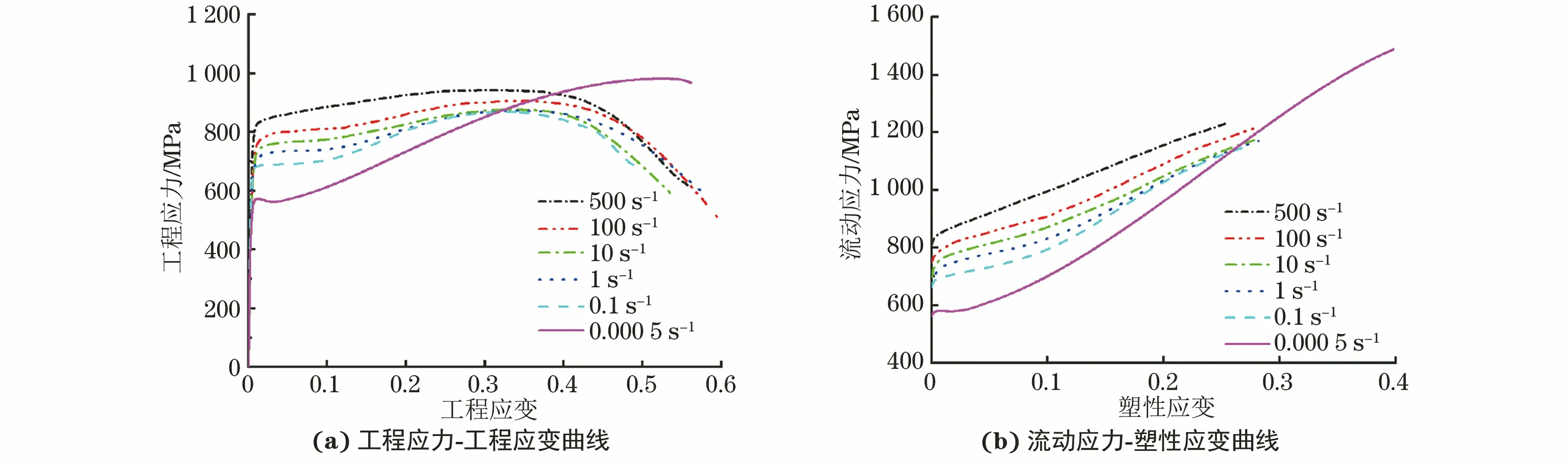
图2 不同应变速率下拉伸时SUS301L-MT不锈钢试样的工程应力-应变曲线和流动应力-塑性应变曲线

2 经典J-C模型

经典的J-C本构模型[15]由描述试验钢应变硬化效应、应变速率效应和热软化效应3部分组成，其表达式为

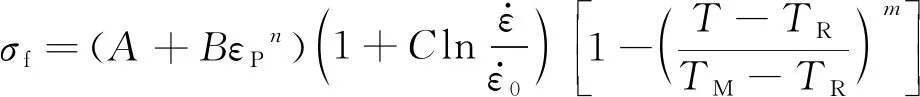
(1)

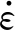
恒定室温条件下，试验钢的塑性变形可视为等温过程，此时有T=TM，则式(1)可变为

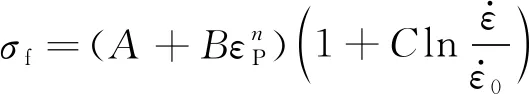
(2)

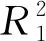
表2 参考应变速率下拟合得到的J-C本构模型参数

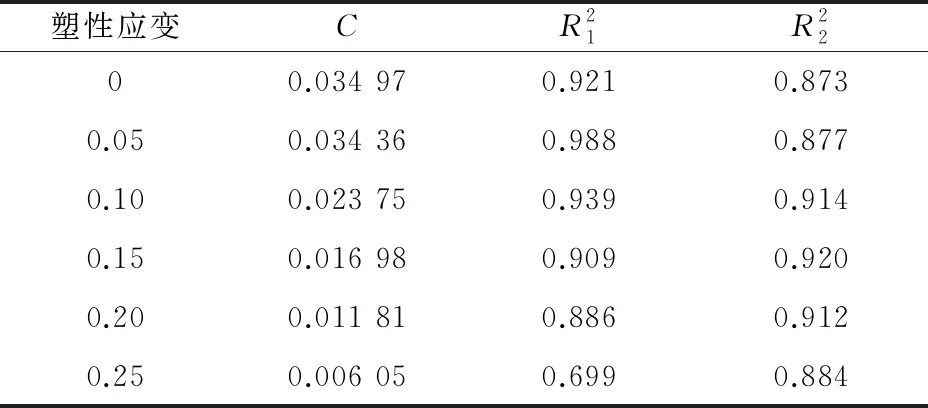
表3 不同塑性应变下拟合得到的J-C本构模型参数

匹配优度通过计算不同应变速率下试验钢在不同塑性应变下拟合应力值与试验应力值的平均相对误差得到，可反映本构模型在不同应变速率下对试验数据拟合的综合优劣程度，其公式为

(3)

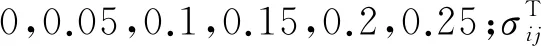
由表3可知，不同塑性应变下拟合得到的应变速率敏感系数差异较大，拟合优度与匹配优度无明显对应关系。这说明采用经典J-C本构模型曲线拟合应变速率敏感系数时，一般只能保证不同应变速率下在选取的固定塑性应变点处拟合效果较好，而不能保证在同一应变速率不同塑性应变下的拟合精度。

分别取拟合优度与匹配优度最大时，即塑性应变为0.05和0.15时拟合得到的C值，及表2中得到的A，B，n值，通过经典J-C本构模型拟合得到流动应力-塑性应变曲线，将其与试验结果进行对比。由图3可以明显看出，无论是使用拟合优度还是匹配优度最佳的应变速率敏感系数，经典J-C本构模型在动态下的拟合效果均较差。

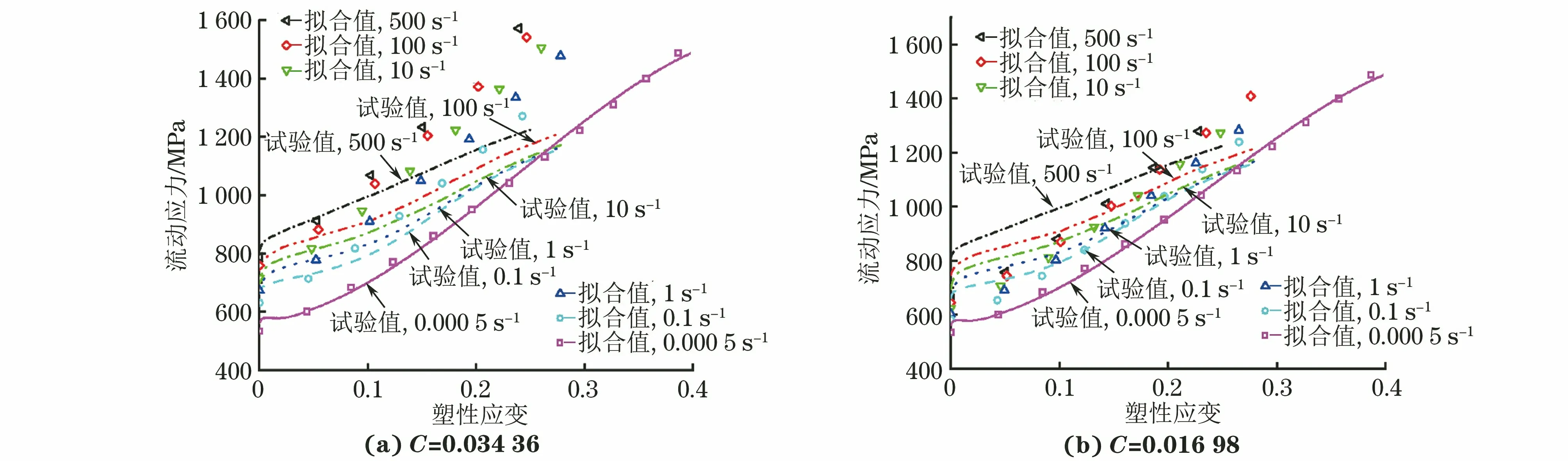
图3 不同应变速率敏感系数下经典J-C本构模型拟合得到试验钢流动应力-塑性应变曲线与试验结果的对比

流动应力放大因子DIF[16]可直观反映出应变速率效应对材料本构关系的影响，其定义为

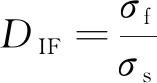
(4)

式中：σs为在准静态应变速率下相同应变所对应的工程应力。

为了更直观地表征不同应变速率下流动应力放大因子对塑性应变的敏感程度，定义了一个新参数——动态放大模量DIM，其表达式为

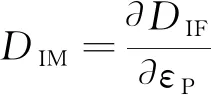
(5)

由图4和图5可以看出，SUS301L-MT不锈钢的流动应力放大因子及动态放大模量均受应变速率与塑性应变的共同影响：在塑性变形的前半阶段，流动应力放大因子随塑性应变的增加而增大，不同应变速率下动态放大模量则较为一致；在塑性变形的后半阶段，流动应力放大因子随塑性应变的增加而减小，不同应变速率下动态放大模量差异较大，均呈先显著下降再缓慢变化的趋势。对于经典的J-C本构模型，应变速率敏感系数为一定值，同时试验钢的动态放大模量DIM值为0，该模型无法反映不同应变速率下马氏体含量随试验钢塑性变形不断变化以及绝热温升软化效应导致的流动应力放大因子DIF和动态放大模量DIM不断变化的现象。

图4 试验钢的流动应力放大因子与塑性应变的关系曲线

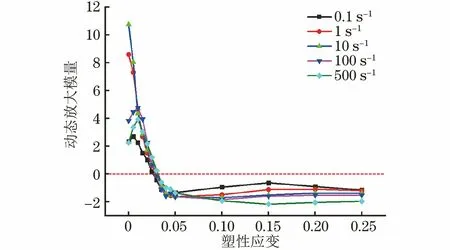
图5 试验钢的动态放大模量与塑性应变的关系曲线

以上现象和分析充分说明，经典的J-C本构模型无法准确拟合流动应力放大因子DIF和动态放大模量DIM变化较为复杂的不锈钢的应力应变关系，其原因是缺乏对不锈钢微观机制的描述，需要针对其局限性对经典J-C本构模型进行改进与修正。

3 基于功热转换机理修正的J-C模型

由图4和图5可知，在不同应变速率下均存在着某一塑性应变量，在该塑性应变前后试验钢的动态放大行为有着截然不同的表征，将该塑性应变量定义为临界应变。SUS301L-MT不锈钢在动态拉伸时绝热温升与应变速率对马氏体相变的影响存在竞争关系，当达到某一塑性应变后，绝热温升的影响更大[4]。将该塑性应变与SUS301L-MT不锈钢在准静态拉伸时开始进行马氏体相变的塑性应变视为一致，并取SUS301L-MT不锈钢在不同应变速率下DIF最大值的均值，即DIM为0时所对应的塑性应变的均值为临界应变。在临界应变前考虑准静态拉伸时试验钢的显微组织主要为原始奥氏体和板条马氏体以及动态拉伸时随应变量的增大试验钢中马氏体相变量增加，在临界应变后考虑准静态拉伸时马氏体相变量增加以及动态拉伸时绝热温升抑制马氏体相变，并基于经典J-C本构模型对准静态行为的描述，对上述两个阶段的准静态拉伸结果分别进行拟合，并保证曲线在分段点光滑连续，即保证两阶段曲线在各个交点处的一阶导数相等，其公式为

(6)

式中：ε0为临界应变；B1，B2，n1，n2为应变硬化参数。

在SUS301L-MT不锈钢动态应力-应变曲线的第一阶段，不同应变速率下该材料的DIF-塑性应变曲线近似为直线或凸型二次曲线，但该阶段塑性应变很小，线性或非线性过程产生的应变在数值上差异很小，故将该阶段的DIF-塑性应变关系视为线性关系，即将经典J-C本构模型中的应变速率敏感系数修正为与应变相关的线性函数，即C=C1ε+ε2。模型修正后的第一阶段本构关系为

(0≤εP≤ε0)

(7)

式中：C1与C2为与应变相关的应变速率敏感系数，可由第一阶段动态拉伸试验曲线拟合得到。

第二阶段时，考虑绝热温升对试验钢的马氏体相变的抑制作用。绝热温升主要是由于金属塑性变形时产生的塑性功转化为内能，而内能没有足够的时间耗散使得材料温度上升造成的。KAPOOR等[17]提出的绝热温升ΔT的计算公式为

(8)

式中：η为功热转换系数；ρ及Cv分别为材料密度及材料比热容。

在进行高应变速率拉伸时，η可取0.9[18-19]，而准静态拉伸可视为等温稳态过程，因此令功热转换系数为一个关于应变速率的函数，即

(9)

得到绝热温升与塑性应变的曲线如图6所示，可以看出，不同应变速率下绝热温升与塑性应变近似为线性关系，且各曲线斜率与应变速率相关。根据以上分析得到绝热温升与塑性应变及应变速率的关系式为

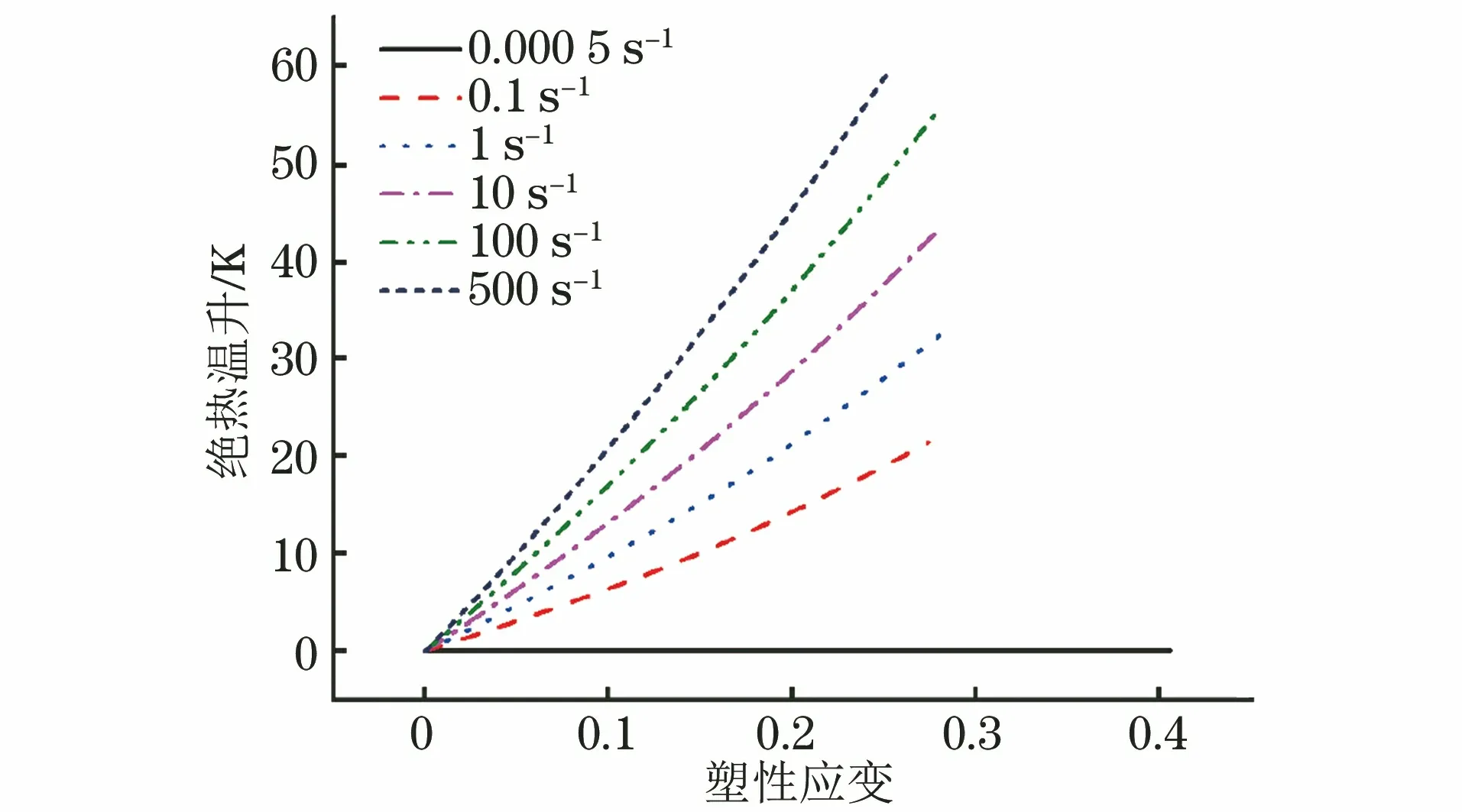
图6 不同应变速率下试验钢的绝热温升与塑性应变的关系曲线

(10)

式中：D为绝热温升影响系数，通过最小二乘法拟合可得D值为16.948。

当绝热温升与塑性应变呈线性关系时，温度项一阶导数与绝热温升的对应关系可类比为前述的DIM与塑性应变的对应关系。SUS301L-MT不锈钢在塑性变形第二阶段的DIM随塑性应变增加而先显著下降再平稳变化。故认为在试验钢塑性变形的第二阶段，由快速拉伸导致的马氏体相变量的增加量不再改变，即应变速率敏感系数重新变为一定值，该值为试验钢塑性变形第一阶段的终止值，此时绝热温升的软化效应占主导作用，且该效应随塑性应变的增大而增大。引用文献[20]中提出的温度软化项，结合前文绝热温升与塑性应变、应变速率的关系，得到第二阶段的本构关系为

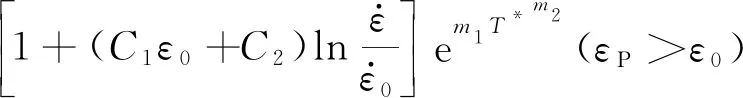
(11)

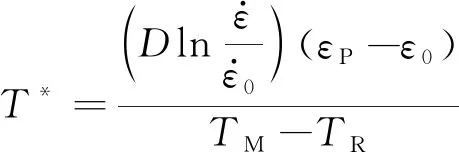
(12)

式中:m1和m2可由第二阶段动态拉伸应力应变曲线拟合得到。

综上所述，SUS301L-MT不锈钢基于功热转换机理修正的J-C模型完整表达式为

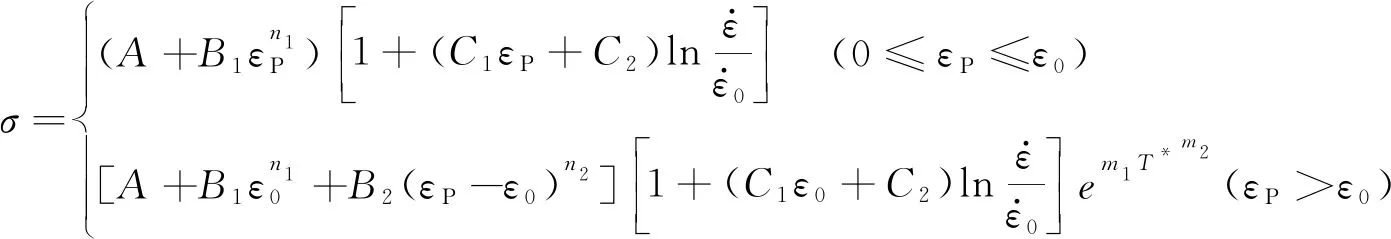
(13)

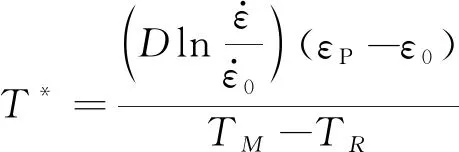
(14)

4 模型验证与讨论

根据上述基于功热转换机理修正的J-C本构关系，仍取参考应变速率为0.000 5 s-1，其中m1与m2取各应变速率下拟合结果的均值，最终确定的各参数见表4。

表4 基于功热转换机理修正的J-C模型参数

将表4中的参数代入式(16)、式(17)，拟合得到的流动应力-塑性应变曲线如图7所示，可以明显看出，基于功热转换机理修正后的J-C本构模型可以较好地反映出SUS301L-MT不锈钢的马氏体相变导致的强化效应及绝热温升导致的软化效应，且与试验结果基本吻合，采用修正模型拟合的匹配优度为0.985，远高于经典J-C本构模型。虽然该修正J-C本构模型拟合参数较多，但对于试验钢在高应变速率下拉伸时诱导马氏体相变及绝热温升抑制马氏体相变等微观机制在其宏观应力-应变关系上的映射相对于经典模型具有一定的优越性。

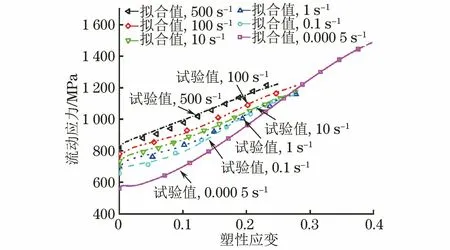
图7 不同应变速率下基于功热转换机理修正J-C本构模型拟合得到的流动应力-塑性应变曲线与试验结果的对比

5 结 论

(1) SUS301L-MT不锈钢具有明显的应变硬化效应，且试验钢的应变硬化效应随着应变速率的增加而减小；高应变速率下试验钢中存在马氏体相变效应和绝热温升效应，其本构关系划分为两个阶段；由于应变速率与随之产生的绝热温升现象对马氏体相变的竞争性影响，试验钢的应变速率强化效应随塑性应变的增加先减弱后趋于稳定。

(2) 引入了动态放大模量DIM，以其值为0时对应的塑性应变定义为临界应变；经典J-C本构模型无法较好地表现SUS301L-MT不锈钢在高应变速率塑性变形时的马氏体相变强化效应和绝热温升软化效应，其对动态拉伸试验数据的拟合效果较差，匹配优度较低。

(3) 基于功热转换机理修正的J-C本构模型第一阶段将流动应力放大因子修正为与应变相关的线性函数，第二阶段考虑了绝热温升软化项，该修正模型与试验结果的匹配优度高达0.985，能较好地表征SUS301L-MT不锈钢的动态拉伸性能。