防旋板结构的迷宫密封转子动力特性研究

薛文松,方志,王天昊,李志刚,李军

(西安交通大学叶轮机械研究所,710049,西安)

环形密封结构是安装在透平机械中转子与静子件之间,在高压差下控制泄漏量的结构。迷宫密封由于其结构简单、加工制造成本低、容易维护更换等优势而在透平机械中广泛应用。然而,相对于孔型密封[1]、袋型密封[2]等阻尼密封结构,迷宫密封更加容易因为转子涡动产生的非定常气流激振力而引起转子稳定性不足[3]。由于进口预旋与转子转动的影响,迷宫密封内部产生的周向旋流对密封交叉刚度具有很大影响[4]。负交叉刚度会产生与转子涡动方向相反的切向气流激振力,交叉刚度的增加表明气流激振力抑制转子向前涡动的能力减弱[5]。

李志刚等发展了基于非定常、动网格的多频涡动模型的密封转子动力特性求解方法,阐明了迷宫密封进口周向旋流是影响密封交叉刚度的主因[6]。同时,李志刚等数值分析了迷宫密封在不同运行工况下转子动力特性系数的变化,表明进口预旋和转速的增加会导致直接刚度与有效阻尼的减小[7]。目前改善透平机械转子动力特性的方法主要有采用阻尼密封结构、调整动静间隙、安装防旋板或旋流控制装置[8],但旋流控制装置不仅安装复杂,而且引入的气流会增加密封泄漏量从而降低透平效率[9]。

Benckert等采用实验方法测量了迷宫密封的直接刚度与交叉刚度,指出进口预旋会导致交叉刚度的增加,在采用进口防旋板之后显著地降低了交叉刚度[10]。Child等通过实验测量了直角与反旋流防旋板结构对迷宫密封转子动力特性的影响,实验表明采用防旋板对迷宫密封的直接刚度与直接阻尼影响有限[11]。Xu等数值研究了防旋板对迷宫密封、袋型密封、孔型密封的转子动力特性系数的影响,结果表明在有进口预旋的情况下加装防旋板对3种密封结构的有效阻尼均有明显提高[12]。Chen等采用多频涡动模型分析了防旋板距密封齿轴向距离对迷宫密封转子动力特性的影响,当轴向距离为零时直接刚度与有效阻尼明显增加[13]。冀大伟等研究了传统防旋板、反旋流防旋板、流线型防旋板对迷宫密封转子动力特性系数的影响,结果表明流线型防旋板能最大地提高有效阻尼[14]。Soghe等研究了防旋板倾斜角、交错角、相对节距对防旋板出口旋流强度的影响,研究表明防旋板倾斜角能够有效地降低密封出口旋流强度,防旋板交错角对防旋板出口旋流强度的影响可以忽略,防旋板相对节距存在最佳值使得防旋板出口旋流强度最小[15]。Iwatsubo等研究了防旋板数目和安装位置对气流周向速度和转子面流体激振力的影响,结果表明当防旋板安装在顺气流流动方向的第一个腔室和第二个腔室时,防旋板对气流周向抑制效果最佳,当防旋板安装在气流出口腔室时,防旋板对气流周向抑制作用不太理想[16]。Sun等研究了不同转速和压比下防旋板高度、数目对密封泄漏量和转子动力特性的影响,指出增加防旋板数目或防旋板高度能够加剧交叉刚度的降低幅度和直接阻尼的增加幅度,从而进一步增加密封转子稳定性[17-18]。Untaroiu等将DOE实验设计方法应用到防旋板几何参数对密封转子稳定性影响的分析上,结果表明气流平均周向速度与防旋板投影到气流流动方向上的长度、交错角以及进口预旋呈明显的二次函数关系[19]。

为了进一步改善迷宫密封的转子动力特性,在迷宫密封中间添加了二级防旋板来进一步降低周向速度,降低交叉刚度并提高有效阻尼。本文采用实验测量一组原始迷宫密封的转子动力特性系数对数值计算结果的准确性进行了验证。在此之后,开展了添加进口带倾斜角防旋板和密封齿间静子带凸台的交错角防旋板结构在两种进口预旋条件下的转子动力特性研究,可为防旋板的设计和优化分析提供参考。

1 实验和数值方法

1.1 实验台简介

(a)密封实验段剖视图

1—激振器;2—静子件;3—电机;4—轴承座; 5—辅助支撑;6—分流管;7—T型平台;8—台架。

图1给出了基于谐波激励机械阻抗法设计建设的密封气流激振转子动力特性实验测量平台。转子通过膜片式联轴器与电机相连,静子件通过激振杆与激振器相连。密封实验段采用对称设计,从而使得气流从静子中部流入、静子左右两侧流出,有利于抵消左右两侧的气流轴向推力。实验台静子采用分体式设计,分为密封实验件、静子套筒、左右两侧静子端盖以及预旋环。为了使预旋环前的进气来流尽可能均匀,实验台在进气口与预旋环之间设置了周向贯通的进气腔。采用两组6根支撑杆进行密封实验段的轴向定位和垂直方向的部分支撑。

压缩机组承担着给密封实验段进口提供具有稳定压力的干燥气流,供气系统由压缩机组、储气稳压罐、旁通阀、冷冻式干燥机、进气阀、热式质量流量计、调节阀以及分流管组成且密封进口压力的改变通过调节阀和旁通阀的共同调节来实现。控制电脑、变频柜以及变频电机给密封转子提供转速。电机自由端布置有转速传感器测量转速。气泵以及轴承油气润滑装置给转子轴承提供连续可靠的油气润滑。控制电脑、功率放大器、激振器等设备给密封静子件提供一定的正余弦激振力,从而使得密封静子偏离中心位置进行小幅度周期性涡动。通过更换带有不同角度预旋孔的预旋环可改变密封进口预旋。进口总温对泄漏量与转子动力特性的影响可以忽略,因此只需通过调节阀和旁通阀来使进口压力相同。由于密封出口与大气相通,所以密封出口静压始终与大气保持一致。

1—温度传感器;2—毕托管;3—静压引压管; 4—电涡流传感器;5—加速度传感器;6—力传感器。图2 实验台测量仪器及安装位置Fig.2 Mesurement system and installation positions

测量系统由传感器、信号采集器以及控制电脑共同组成。图2给出了密封静子件上所需布置的测量仪器,包括Pt100铂电阻温度传感器、毕托管、静压引压管等静态测量仪器,以及电涡流位移传感器、压电式加速度传感器、压电式力传感器等动态测量仪器。密封进口压力采用毕托管进行测量,测量过程中需要将总压孔正对切向来流方向,然后将毕托管总压孔中的气流引入到压力传感器中进行测量,与此同时,密封进口腔室内壁面静压通过静压引压管引入到压力传感器中进行测量。表1给出了实验中直接测量到的物理量以及所用仪器的精度,根据误差传递公式计算得到刚度系数与阻尼系数的相对误差为±(5%～20%)。

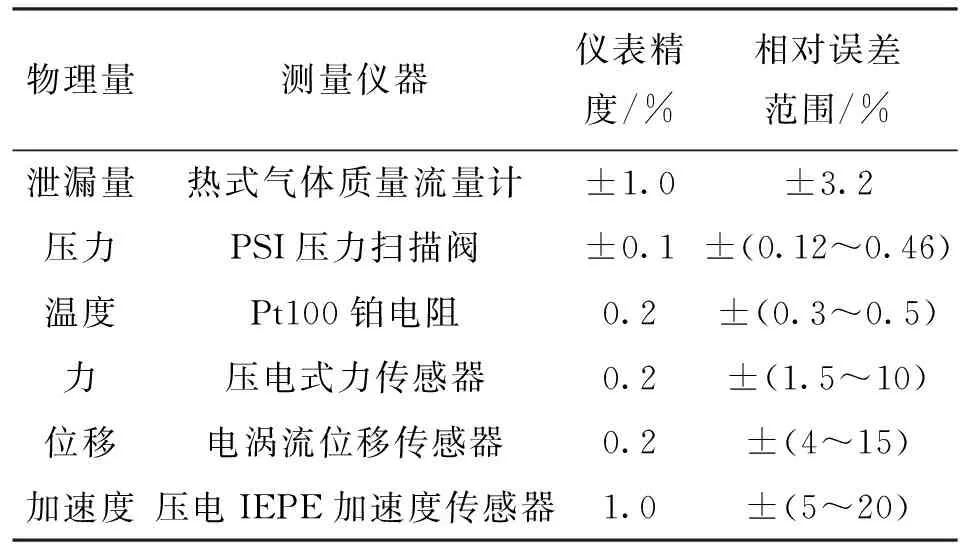
表1 直接测量物理量及精度

1.2 测量方法

在实验台无转速且无气流通过的情况下,进行密封静子件激励实验以测量实验台的基准刚度系数与基准阻尼系数。在每一个测量频率下通过控制两侧激振力的大小分别进行两组互不相关的x方向激励与y方向激励。当激振力达到给定数值时记录密封静子件的激振力、加速度、涡动位移随时间的变化。根据测量得到的数据,通过编程迭代使两个方向的直接刚度频率无关并得到正确的静子质量[Ms],在此基础上得到实验台基准动力系数Hij_bl。根据小位移涡动理论可知,对于工质为理想空气的密封结构而言,密封腔室内作用在转子上的气流激振力与转子涡动位移存在如下关系

(1)

(2)

(3)

其中Ω为涡动频率。

采用FFT变换将方程(1)中时域信号下的转子气流激振力和涡动位移转化为频率信号进行求解,则频域求解的力-位移方程为

(4)

式中H=K+jΩC为密封阻抗系数。

实验测量过程中密封腔室内气流激振力可以通过对静子件受力分析得到,如下所示

(5)

式中:下标x表示激励的方向;下标y表示流体激振力、转子位移、加速度的方向。

实验台中密封实验件左右对称布置,因此实验台系统动力系数减去实验台基准动力系数的一半即为密封件内气流激振力产生的转子动力特性系数Hseal,即

Hseal=Hts-Hbl

(6)

式中:下标ts表示实验台系统;bl表示实验台基准。

直接阻尼系数和交叉刚度系数是切向力的来源,所以它们对转子系统的稳定性具有重要影响。为了综合衡量交叉刚度与直接阻尼对转子向前涡动的影响,通常引入密封有效阻尼来综合评价密封转子稳定性,有效阻尼定义[5]如下

Ceff=Cxx-Kxy/Ω

(7)

1.3 密封模型

采用设计的两种预旋环来得到进口预旋比。两种预旋环的内径为92 mm、宽度为30 mm。在预旋环轴向中心位置沿周向平均分布有72个直径为2 mm的通孔,通孔的轴向与预旋环的径向夹角分别为0°和60°。

图3 密封几何尺寸及实验件Fig.3 Labyrinth seal geometry and test seal

图3给出了迷宫密封几何尺寸及实验件。密封转子长度为266 mm、直径为170 mm,齿数为14,齿顶宽度为0.3 mm、齿根宽度为2.288 mm,密封间隙为0.3 mm,齿间距为5 mm,腔室深度为4.01 mm。无防旋板的原始迷宫密封命名为Design 1。

根据迷宫密封的平均周向速度沿轴向的变化规律设计了进口防旋板与二级防旋板,如图4所示。进口防旋板与二级防旋板整圈均为90个。为了应对迷宫密封进口的高预旋,进口防旋板采用带有40°倾斜角(防旋板绕顶部顺旋转方向倾斜为负,逆旋转方向倾斜为正)。倾斜角防旋板在尾缘处沿反旋转方向流动的气流会引导气流从尾缘向前缘流动,从而在齿前缘附近产生了负旋流强度。随着进口预旋增加,防旋板通道内涡流强度增强,产生的负旋流强度越大。改变Design 1第一个密封齿的齿型并设计进口防旋板的结构,命名为Design 2。

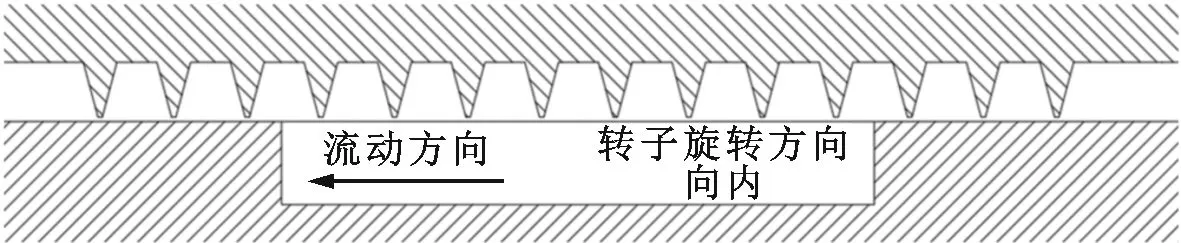
(a)Design 1几何结构

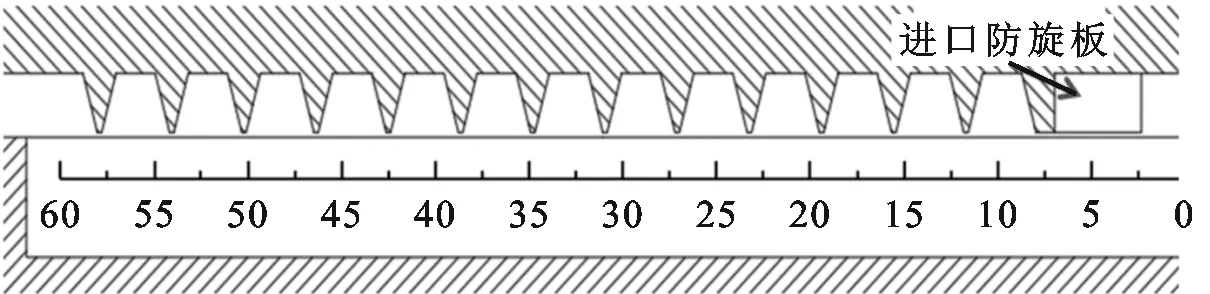
(b)Design 2几何结构

(c)Design 3几何结构图4 3种迷宫密封结构子午面示意图Fig.4 Cross section of three labyrinth seals

由于二级防旋板不改变转子结构,考虑到迷宫密封间隙射流速度远大于腔室内的流速,仅在进口设计防旋板不足以明显改变旋流强度,因此将二级防旋板之前的一个迷宫齿间隙调整为1.0 mm,同时在静子件上设计凸台,保持二级防旋板径向高度为0.7 mm,密封间隙为0.3 mm。由于在采用零预旋环带有进口防旋板的工况下,密封内部气流受到转子转动黏性拖拽作用在第5个密封齿附近的平均周向速度升高到了进口防旋板上游的大小。在保持进口防旋板的基础上将第5个密封齿设计为二级防旋板来进一步降低平均周向速度,该结构命名为Design 3。在图4b中给出了提取平均周向速度的60个截面轴向位置,图4c中给出了提取云图的3个截面位置。

1.4 数值方法及验证

图5给出了Design 3的几何模型,预旋环及进气管侧设为对称交界面。在4根进气管道设置进口边界条件,总压300 kPa,总温20 ℃,出口设为静压100 kPa。

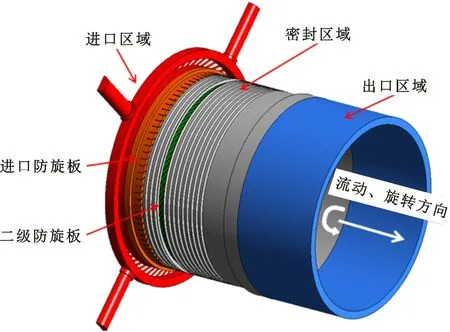
图5 Design 3计算模型Fig.5 Computational model of Design 3 preswirl ring

分别对进气管、预旋环、防旋板、密封段进行结构化网格划分,对壁面进行加密处理使y+保持在100以内以满足k-ε湍流模型的需要。当非定常计算的动量方程和湍流方程的残差下降到10-5、转子面上的受力Fx和Fy成周期性振荡,且相邻周期的受力波动小于0.2%时,认为计算收敛。图6给出了密封模型的计算网格。

(c)二级防旋板 (d)密封区域图6 Design 3不同区域计算网格Fig.6 Computational mesh of various parts of Design 3 preswirl ring

为了评价密封进口旋流大小,定义进口预旋比为

λ=60Vt/πDn

(8)

式中:Vt为密封进口的气流周向速度;D为转子直径。

9 000 r/min转速下,60°预旋环时密封进口的平均周向速度为105.7 m/s、预旋比为1.32,0°预旋环时密封进口的平均周向速度为10.2 m/s、预旋比为0.13。采用基于转子多频椭圆涡动模型的非定常数值方法来进行RANS方程求解。动网格技术是通过网格变形技术实现的,可以人为给定转子的运动。基于动网格技术的三维非定常CFD已被应用于求解迷宫密封内部三维瞬态流场、非定常流体激振力和频率相关的转子动力特性系数。相比于实验方法和Bulk Flow方法,CFD方法具有不受物理模型限制、可给出密封内部流场细节等优点,还可进一步提高对转子动力特性系数的预测精度。阻尼密封的转子动力特性系数具有很强的频率相关性,研究其随频率的变化规律对掌握转子动力特性具有重要作用,基于动网格技术的三维非定常CFD技术可以求解宽频域下的转子动力特性系数。

非定常计算过程中给定转子的多频椭圆涡动轨迹,且每个频率组分下椭圆涡动轨迹长轴均为密封初始间隙的1%,短轴为密封初始间隙的0.5%。表2给出了非定常计算方法以及多频椭圆涡动模型参数设置。

表2 转子动力特性非定常数值求解方法

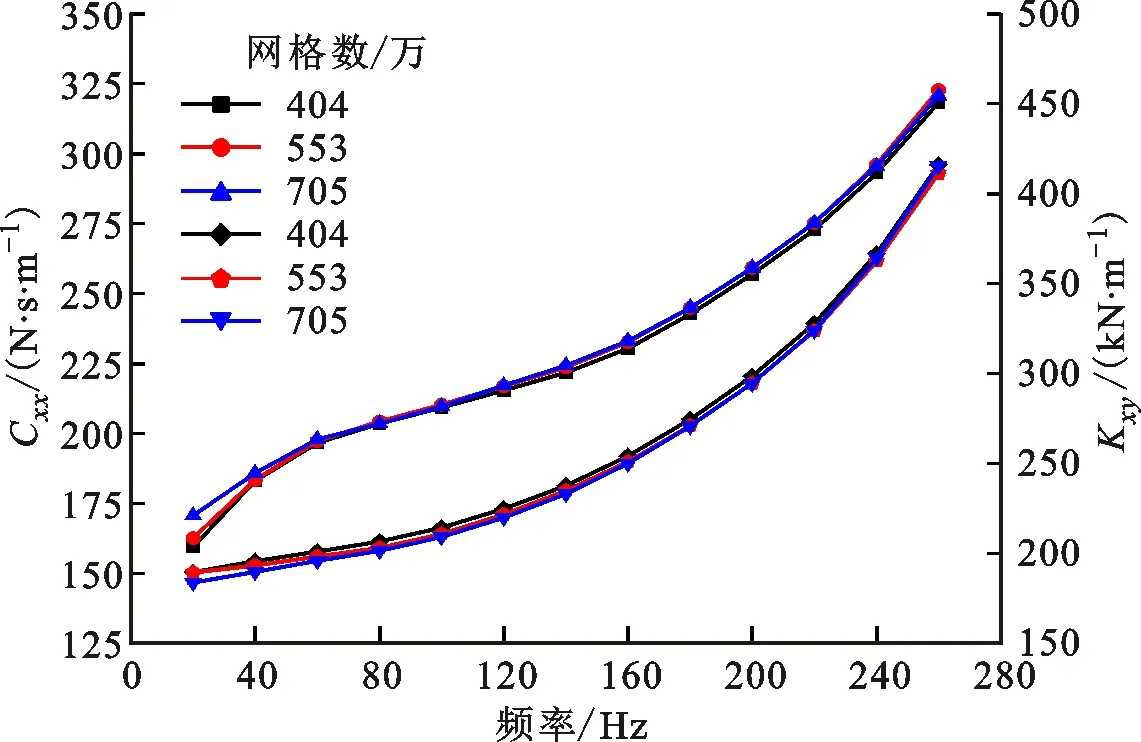
图7 Design 1不同网格数的直接阻尼与交叉刚度Fig.7 Direct damping and cross-coupling stiffness of Design 1 at different meshes

采用3种不同网格数(404万、553万、705万)对预旋比为1.32的Design 1结构进行网格无关性验证。在不同网格数下泄漏量均为0.0378 kg/s,其差别小于0.3%。图7给出了直接阻尼、交叉刚度随网格数的变化。就直接阻尼而言,当网格数从404万增加至553万时,密封直接阻尼在整个涡动频率范围内略微增加,约为0.37%～1.98%;当网格数从553万继续增加至705万时,密封直接阻尼在涡动频率为80、100、240、260 Hz时略微减小,在其余涡动频率范围内略微增加,变化范围为-0.63%～4.92%。就交叉刚度而言,当网格数从404万增加至553万时,交叉刚度在涡动频率范围内降低1.67%以内;当网格数从553万继续增加时,交叉刚度在涡动频率低于180 Hz时降低,在涡动频率高于180 Hz时增加,变化范围为-2.98%～1.04%。综合考虑网格数对计算准确性与计算资源的影响,包括预旋环、防旋板、迷宫密封的整体结构的计算网格数约为553万。

(a)直接刚度与交叉刚度

(b)直接阻尼与有效阻尼图8 刚度系数与阻尼系数的CFD与实验结果对比Fig.8 Rotordynamic coefficients vs whirling frequency

图8给出了Design 1的实验测量数据与数值结果的比较,该两组数据的预旋环与密封进口之间的静压保持为400 kPa,出口静压为100 kPa。为了避免振动频率靠近了系统的固有频率而产生共振,实验过程中在10～70 Hz、110～145 Hz的频率范围每隔5或10 Hz测量一次转子动力特性系数。如图8所示,数值模拟得到的直接刚度系数略比实验结果偏高,阻尼系数和交叉刚度与实验结果吻合得很好。数值预测结果和实验测量数据总体上吻合良好,验证了数值方法的可靠性。

2 结果分析

2.1 防旋板对周向平均速度的影响

选取包含进口防旋板及迷宫密封段的轴向位置,等距选取60个垂直于轴向的截面,如图4b所示。在每个截面提取出质量平均周向速度,图9给出了Design 1、2、3密封腔室及防旋板内气流平均周向速度沿轴向的分布。

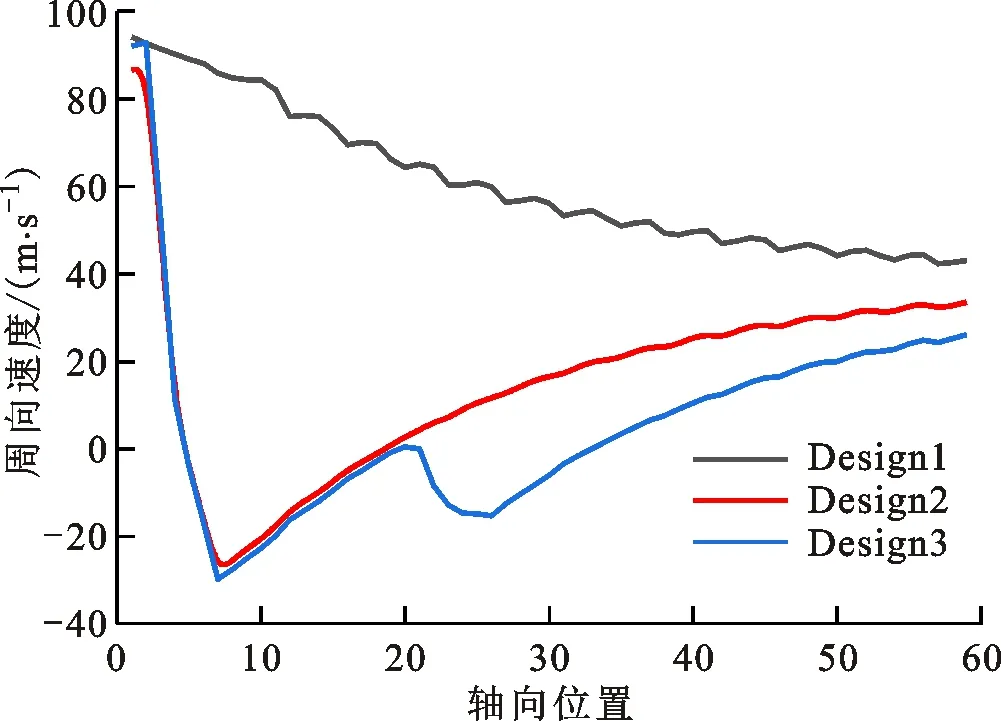
(a)预旋比为1.32时气流平均周向速度分布

(b)预旋比为0.13时气流平均周向速度分布图9 气流平均周向速度沿不同轴向位置分布Fig.9 Circumferential velocity vs axial position at seal cavities

研究发现在Design 1结构中,预旋比为1.32时气流平均周向速度沿轴向减速下降、预旋比为0.13时气流平均周向速度沿轴向减速增加,这是密封腔室内气流在转子面黏性力周向拖动作用下的结果。另一方面,气流平均周向速度会在进口防旋板段内快速下降之后沿轴向减速增加,且在预旋比为1.32时进口防旋板能达到的最小周向速度为-27.9 m/s,优于预旋比为0.13时的-2.9 m/s。在密封进口腔室设计防旋板结构的Design 2中,上游携带高进口预旋的气流冲击防旋板压力面,从而在齿前缘附近产生了负旋流。高进口预旋,防旋板通道内涡流强度增强引起齿前缘附近逆旋转方向周向平均速度增加,在Design 3中的二级防旋板则采用逆旋转方向交错角的导流作用来降低间隙射流的平均周向速度。

2.2 防旋板对泄漏量的影响

表3列出了3种迷宫密封结构在高低2种预旋比下的泄漏量。6个工况下的进口总压为300 kPa,总温为20 ℃,出口静压为100 kPa。在相同的边界条件下高预旋比使泄漏量下降了约3.6%。类似于迷宫密封随着转速增加泄漏量减小,在高进口预旋比时迷宫密封进口的高速旋转带动密封腔室中的流体周向流动,同时密封齿在轴向的阻隔,在密封腔室中形成强烈的旋涡流动,使气流的动能有效地耗散为内能,从而使泄漏量减小。设计第二级防旋板为了提高导流作用将上一个密封齿的间隙增加到1.0 mm,因此导致泄漏量的增加,在预旋比为0.13时泄漏量增加约1.1%,在预旋比为1.32时增加约2.0%。

表3 3种密封结构在两组进口预旋比下的泄漏量

2.3 预旋比为1.32时防旋板对转子动力特性的影响

图10给出了进口防旋板和二级防旋板对迷宫密封刚度系数的影响,并给出了Design 1结构的刚度系数作为对比分析。当密封进口腔室设计进口防旋板后,Design 2相对于Design 1的直接刚度均显著增加,表明进口防旋板能够使得直接刚度产生的径向向内的激振力增加,从而进一步限制转子径向向外移动,提高密封转子的聚中能力。设计二级防旋板的Design 3相对于Design 2的直接刚度略微下降,但其直接刚度仍明显大于Design 1结构,因此相比Design 1结构,Design 2、3结构使密封在进口预旋比为1.32时仍能提升转子聚中能力。

图10 预旋比为1.32时防旋板结构对直接刚度的影响Fig.10 Direct stiffness coefficients vs whirling frequency at the inlet preswirl ratio of 1.32

如图11所示,比较3种密封结构,Design 1结构沿轴线分布的平均周向速度最大,因此具有最大的交叉刚度。当设计进口防旋板结构后,Design 2相对于Design 1的交叉刚度大幅降低,且降幅达到63.3%～86.3%,这将使得交叉刚度产生的与转子涡动方向相同的正切向激振力降低,有利于密封转子稳定运行。当设计二级防旋板时,Design 3相对于Design 2的交叉刚度降低了12.9%～39.4%,即设计进口防旋板与二级防旋板能够削弱交叉刚度产生的与转子涡动方向相同的正切向激振力,从而增加迷宫密封转子稳定性。

图11 预旋比1.32时防旋板结构对交叉刚度的影响Fig.11 Cross-coupling stiffness coefficients vs whirling frequency at the inlet preswirl ratio of 1.32

图12给出了防旋板对迷宫密封直接阻尼系数的影响。设计进口防旋板时,防旋板结构对迷宫密封直接阻尼系数几乎没有影响,Design 2结构相比Design 1的直接阻尼变化范围在-2.3%～17.6%之间,相比Design 2,Design 3的直接阻尼增加17.7%～22.6%,表明二级防旋板结构增加了迷宫密封直接阻尼产生的与转子涡动方向相反的负切向激振力。

图12 预旋比为1.32时防旋板结构对直接阻尼的影响Fig.12 Direct damping coefficients vs whirling frequency at the inlet preswirl ratio of 1.32

图13给出了进口防旋板和二级防旋板对迷宫密封有效阻尼系数的影响。Design 1的有效阻尼系数穿越频率为175.1 Hz,即有效阻尼在涡动频率低于175.1 Hz时为负值,表明作用在转子上的净切向激振力与转子涡动方向相同,从而可能诱发转子失稳。当设计进口防旋板结构后,显著下降的交叉刚度最终使得Design 2结构的有效阻尼增加,且有效阻尼项穿越频率从175.1 Hz降低到28.3 Hz,即迷宫密封安全稳定运行的频率范围在进口防旋板引入后明显增加。在设计了两级防旋板的Design 3中,迷宫密封有效阻尼进一步增加,有效阻尼项的穿越频率消失。相比Design 2,Design 3具有更大的转子涡动频率安全范围,从而具有更加优越的迷宫密封转子稳定性。

图13 预旋比为1.32时下防旋板结构对有效阻尼的影响Fig.13 Effective damping coefficients vs whirling frequency at the inlet preswirl ratio of 1.32

2.4 预旋比为0.13时防旋板对转子动力特性的影响

图14给出了预旋比为0.13时防旋板结构对迷宫密封直接刚度的影响。3种结构的直接刚度相对于预旋比为1.32时有明显增加,说明高进口预旋会降低迷宫密封转子的聚中能力。设计进口防旋板和二级防旋板对迷宫密封的直接刚度的影响与预旋比为1.32时类似,其中Design 2增加直接刚度的能力最大。

图14 预旋比为0.13时下防旋板结构对直接刚度的影响Fig.14 Direct stiffness coefficients vs whirling frequency at the inlet preswirl ratio of 0.13

图15给出了预旋比为0.13时防旋板结构对迷宫密封交叉刚度系数的影响。Design 1在预旋比为0.13时的交叉刚度在240 Hz以下时均小于0,同时相比高预旋比1.32工况时进口防旋板结构Design 2对降低交叉刚度的能力明显减弱。Design 1在预旋比为0.13时相比预旋比为1.32时交叉刚度下降了97.0%～113.8%,且频率越小下降越多。在迷宫密封齿中段设计二级防旋板的Design 3,交叉刚度的绝对值相对于Design 2在不同频率下增加了24.4%～153.0%。

图15 预旋比为0.13时防旋板结构对交叉刚度的影响Fig.15 Cross-coupling stiffness coefficients vs whirling frequency at the inlet preswirl ratio of 0.13

图16给出了预旋比为0.13时防旋板结构对迷宫密封直接阻尼系数的影响。Design 1在预旋比为0.13时相对于预旋比为1.32时直接阻尼下降了6.3%～25.2%,且频率越高下降越多,Design 2相比Design 1直接阻尼增加了14.3%～21.4%。设计二级防旋板对迷宫密封的直接阻尼提高的幅度与进口防旋板相当,在20 Hz之后Design 3相比Design 2直接阻尼增加了12.6%～34.6%。

图16 预旋比为0.13时防旋板结构对直接阻尼的影响Fig.16 Direct damping coefficients vs whirling frequency at the inlet preswirl ratio of 0.13

图17给出了预旋比为0.13时防旋板结构对迷宫密封有效阻尼系数的影响。预旋比为0.13时在20 Hz之后,Design 2相比Design 1的有效阻尼增加31.6%～60.0%,Design 3相比Design 2的有效阻尼增加26.9%～38.0%。对比图13与图17,低预旋比时设计了二级防旋板对增加有效阻尼的效果与添加进口防旋板类似,因此在低预旋时二级防旋板对有效阻尼提升效果更好。

图17 预旋比为0.13时防旋板结构对有效阻尼的影响Fig.17 Effective damping coefficients vs whirling frequency at the inlet preswirl ratio of 0.13

2.5 防旋板对流场的影响

图18为进口防旋板在预旋比为1.32、0.13时沿轴向截面的周向速度云图与矢量图。在预旋比为1.32时气流沿旋转方向冲击防旋板后逆时针流动,并在周向上一个防旋板与转子的间隙中向逆转动方向流动,产生了反向旋流。在预旋比为0.13时由于气流对于防旋板的冲击减弱,防旋板腔室中的涡流强度减弱使周向速度仅降低至-10.7 m·s-1。

(a)预旋比为1.32时进口防旋板内部流场

(b)预旋比为0.13时进口防旋板内部流场图18 Design 2(截面1)周向速度云图及速度矢量图Fig.18 Circumferential velocity contours and streamlines in the section 1 of Design 2

图19为Design 3截面2中二级防旋板内不同轴向位置的周向速度云图。由于二级防旋板与转子保持了0.3 mm的间隙,因此在间隙内气流仍保持着较高的与转子旋转同向的周向速度。二级防旋板仅对0.7 mm内的气流沿反旋转方向进行导流。

图19 Design 3(截面2)周向速度云图Fig.19 Circumferential velocity contours in the section 2 of Design 3

图20给出了x方向激励、t=0.1 s时截面3上静压分布云图以及转子激振力相位图。在x方向激励、t=0.1 s时,转子涡动至x方向最大位移处且涡动速度与y方向平行。气流激振力与实际情况保持相同相位,力矢量长度按照相同比例缩放。

(a)Design 1 (b)Design 2

(c)Design 3 图20 预旋比为0.13时截面3静压云图及气流激振力 相位图(x方向激励、t=0.1 s)Fig.20 Static pressure contours in section 3 and response forces acting on the rotor for three brake configurations at the inlet preswirl ratio of 0.13

Design 1的径向气流激振力方向与位移方向相同不利于转子聚中,这和直接刚度在高频下为负值有关。与Design 1相比,Design 2的径向气流激振力下降了59.2%,说明进口防旋板能有效改善迷宫密封转子聚中能力。Design 3的径向气流激振力相比Design 1下降19.9%,不同结构激振力大小与直接刚度的相对大小一致,直接刚度越大径向气流激振力越小。

相对于径向气流激振力,切向气流激振力在不同的结构下变化更为明显。Design 1的切向气流激振力的方向与转子旋转方向相反,因此切向气流激振力越大越有利于减小涡动。设计进口防旋板的Design 2切向气流激振力增加55.6%,Design 3的切向气流激振力相对于Design 2增加46.8%,说明设计进口防旋板、二级防旋板均有利于提升迷宫密封转子稳定性。切向气流激振力与有效阻尼变化规律一致,切向气流激振力越大有效阻尼越大。

3 结 论

通过研究高低两种预旋比下无防旋板结构迷宫密封、进口设计防旋板迷宫密封和进口与二级防旋板设计的迷宫密封气流激振转子动力特性,得到如下结论。

(1)高预旋比1.32会导致无防旋板结构迷宫密封Design 1的直接刚度和有效阻尼减小,而交叉刚度和直接阻尼增加。高预旋比削弱了迷宫密封转子聚中能力,也弱化了抑制转子涡动的能力。同时迷宫密封的直接刚度越大与位移方向相同的径向气流激振力越小,有效阻尼越大与涡动方向相反的切向气流激振力越大。

(2)进口设计防旋板迷宫密封Design 2在高预旋比1.32时显著影响转子动力特性,大幅降低交叉刚度并使有效阻尼增加,且在防旋板出口平均周向速度相较预旋比为0.13时降低更明显。预旋比为1.32时Design 2相比于Design 1交叉刚度下降了63.3%～86.3%,有效阻尼的穿越频率从175.1 Hz降低到28.3 Hz。2种高低预旋比下设计进口防旋板均能提高迷宫密封的直接刚度,增强转子聚中能力。

(3)在进口防旋板的基础上,设计二级防旋板的迷宫密封Design 3相比于Design 2会略微降低迷宫密封的直接刚度,但仍大于Design 1结构。设计二级防旋板会降低迷宫密封的交叉刚度,增加直接阻尼。