用于全色锐化的相对平均生成对抗网络

陈婷,王松涛,高涛,刘梦尼,陈友静

(长安大学信息工程学院,710000,西安)

为充分利用不同传感器图像之间的互补特征,一些图像融合技术被相继提出[1-3]。作为遥感图像融合的一种方式,全色锐化可将低空间分辨率的多光谱(LRMS)图像和高空间分辨率的全色(PAN)图像进行融合,从而获得高分辨率多光谱(HRMS)图像,目前已被广泛用于目标检测、土地覆盖分类[4-5]等领域。然而,遥感卫星对地面同一区域拍摄时,仅能获得一对LRMS图像和PAN图像,导致遥感图像信息无法被充分利用。因此,如何通过图像融合来获得HRMS图像已经成为遥感图像处理领域的研究热点之一。

目前,全色锐化算法可大致分为4类[6-7]。第1类是基于成分替代的全色锐化算法,最具有代表性的算法是基于强度色调饱和度(IHS)的全色锐化算法[8]。该算法通过将原始多光谱图像从RGB空间转换到IHS空间,并使用PAN图像代替IHS空间的强度(intensity)分量,由此得到全色锐化图像。由于该变换只适用于三通道图像,Rahmani等提出了AIHS算法,使该变换更适用于多通道图像[9]。然而,基于成分替代的全色锐化算法普遍存在融合图像光谱失真的现象。第2类是基于多分辨率分析的全色锐化算法:King等将小波变换用于全色锐化获得融合图像[10];Liu J.等提出了一种基于平滑滤波器的强度调制(SFIM)来调节注入的空间细节[11]。但是,该类算法过于依赖图像配准的准确性。与第1类算法相比,基于多分辨率分析的算法能够有效保持光谱信息,但容易造成融合图像空间失真。第3类是基于变分模型的全色锐化算法,该类算法根据先验知识进行假设,并通过最优解得到融合结果。Tian等提出了基于梯度稀疏表示的变分全色锐化算法,取得了良好的效果[12]。然而,该类算法需要合理的假设,否则容易导致融合图像产生失真。第4类是基于深度学习的全色锐化算法。Masi等提出了基于卷积神经网络的全色锐化算法(PNN)[13],将3层简单超分辨率网络用于全色锐化,但该算法只是将全色锐化问题当作深度学习的一个黑盒子,缺乏合理的物理解释。为此,He等将基于成分替代/基于多分辨率分析模型在一个统一的细节注入框架中表示,使提出的网络结构具有明确的物理解释[14]。然而,这种将原图像以堆叠方式输入网络的算法忽略了LRMS图像与PAN图像间的显著性差异,不利于特征提取。Liu X.等利用两个3层子网络分别提取原图像的层次特征来获取PAN图像和LRMS图像之间的互补信息,并在特征维度对图像进行融合重建,使融合后的图像取得了良好的效果[15]。Shao Z. F.等利用两个不同深度的卷积层分别从PAN图像和LRMS图像中提取空间特征和光谱特征[16]。另外,在深度学习算法中,由于对抗网络(GAN)能够生成现实中不存在的图像而被用于全色锐化[17]。Liu Q.等提出了PSGAN,首次将GAN用于全色锐化[18]。在此基础上,Shao Z. M.等提出了残差编解码器条件生成对抗网络(RED-cGAN),将自编码器与GAN相结合以保持光谱信息和空间信息[19]。

虽然基于深度学习的全色锐化算法在全色锐化问题中取得了进展,但依然存在对原图像特征提取不充分而导致细节信息丢失,以及忽略了特征间的差异而导致特征冗余并产生融合失真的问题。针对这些问题,本文基于相对平均生成对抗网络(RaGAN)[20]提出了一种用于全色锐化的相对平均生成对抗网络(Pan-RaGAN),融合后的图像具有更多的空间细节信息和光谱信息。

1 相关内容

1.1 相对平均生成对抗网络

GAN的基本思想是通过生成器与鉴别器之间的对抗博弈使生成器生成足以以假乱真的假样本,网络结构如图1所示。

图1 生成对抗网络结构Fig.1 Architecture of GAN

为解决GAN生成图像质量不高以及训练过程不稳定的问题,一些GAN的变体被相继提出[20-23]。相对平均鉴别器的使用有助于生成器恢复更真实的图像纹理细节,相对平均鉴别器的函数表达式为

DRa(xr,xf)=σ(S(xr)-Exf[S(xf)])→1

(1)

DRa(xf,xr)=σ(S(xf)-Exr[S(xr)])→0

(2)

Exf[ln(1-DRa(xf,xr))]

(3)

Exf[ln(DRa(xf,xr))]

(4)

1.2 特征提取

基于深度学习的全色锐化网络输入方式通常有堆叠的输入结构和两流输入结构这2种。PNN使用堆叠的方式将PAN图像与LRMS图像进行堆叠,形成多通道图像作为网络输入。PSGAN使用两流的3层结构作为网络输入,分别提取PAN图像与LRMS图像的特征。与堆叠的输入结构相比,两流输入结构虽然能够提升网络的性能,但由于网络结构简单,导致特征提取不足,如果通过增加网络的深度来提取特征会造成网络训练困难等问题。Huang等提出了一种密集块体系结构,在可以提取更多特征信息的同时改善了网络中的信息流和梯度,使网络易于训练[24]。因此,本文提出使用密集块作为网络结构的特征提取模块。

1.3 注意力机制

注意力机制通过网络学习得到一组用于保留感兴趣特征的权重参数,同时能够抑制不必要的特征。陈一鸣等将注意力机制应用于低级视觉处理任务,并取得了成功[25]。在全色锐化问题中,本文利用空间注意力机制对特征进行重新分配权重,从而获得了更多有用的细节信息作为融合图像的高频信息,有效地增强了细节信息的融合。Hu等提出由两个卷积层构造的空间注意力单元(SA),其结构如图2所示[26]。定义C表示图像的通道数,W和H表示图像的宽和高,SA中的卷积核尺度为1×1,输出特征通道数分别为C×n和1,n为增加通道数的比例,本文设置为2。若X是空间注意力模块的输入,尺寸为H×W×C,则空间注意力掩模α表示为

α=σ(W2*δ(W1*X+b1)+b2)

(5)

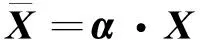
(6)

图2 空间注意力单元结构Fig.2 Architecture of spatial attention unit

2 用于全色锐化的相对平均生成对抗 网络

Pan-RaGAN网络结构如图3所示,生成器网络包括特征提取、特征融合、特征细化和特征重建共4个部分,主要用于生成HRMS图像。鉴别器结构使用全卷积网络进行构建,主要用于判断图像是否为生成器生成的图像。

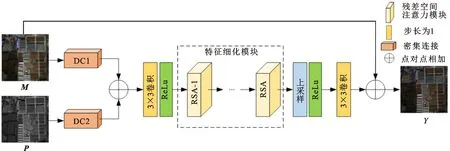
(a)生成器

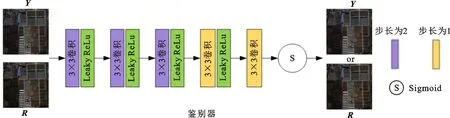
(b)鉴别器图3 Pan-RaGAN网络结构Fig.3 Architecture of Pan-RaGAN

2.1 特征提取模块

由于PAN图像只含有一个较长波段范围的波段而LRMS图像由多个不同波长范围的波段组成(本文选用的GF-2卫星和QB卫星的LRMS图像具有4个通道),因此通常认为PAN图像具有丰富的空间信息,LRMS图像具有更多的光谱信息。为充分利用原图像空间和光谱信息,Liu X.等在两流输入结构中使用3层卷积网络来提取PAN图像与LRMS图像的互补信息[15],这会导致对原图像特征提取不充分并最终影响融合效果。由于批归一化(BN)层在GAN网络训练下会产生伪影,缺少稳定性[18],因此本文对密集块[24]进行改进,剔除原密集块中的BN层,得到密集连接结构如图4所示。

在模块开始端输入原图像,将每个卷积层的输出都作为后面卷积层的输入,卷积层的输出特征表示为

(7)

图4 密集连接结构Fig.4 Architecture of dense connection

式中:Hi(·)表示Conv-ReLu运算;[·]表示张量连接运算(concat);i={1,2,…,K}表示第i个卷积层,K表示卷积层总数,本文设置K=4;xi表示第i个卷积层的输出特征;x0表示输入的图像。最终,得到改进的密集块输出为

Ffe=fDC[x1,…,xK]

(8)

式中fDC表示张量连接运算函数。

本文利用DC模块形成用于提取原图像特征的两流输入结构,如图3a中的DC1和DC2所示,通过这种输入结构尽可能多地利用原图像的中间层特征。两个密集块具有相同的结构不同的权值,由于PAN图像与LRMS图像具有不同的通道数量,因此密集块输入层的特征通道数分别为1和4。

2.2 特征融合模块

为了将提取的特征进行融合,大多数算法使用张量连接将提取的特征进行拼接,然后送入下一卷积层进行处理,本文使用像素相加的融合策略将两个独立分支提取的PAN图像空间信息和LRMS图像光谱信息进行融合,该融合规则相比张量连接可以减少模型的参数。像素相加的融合策略可表示为

(9)

2.3 特征细化模块

生成器网络的核心在于学习目标图像与LRMS图像之间的残差信息,这些残差信息主要包含图像的高频细节信息和少量的光谱信息,而特征提取融合后的信息对残差信息的构建具有不同的作用。为了从融合的特征中选择出PAN与LRMS图像的互补信息同时剔除冗余信息,本文通过特征细化模块对融合的特征重新分配权重,对残差信息构建贡献度较大的特征分配较大的权值,对残差信息构建贡献度较小的特征分配较小的权值,从而有效地选择出高频信息。

(10)

图5 特征细化模块Fig.5 Module of feature refinement

2.4 图像重建模块

图像重建模块包含一个上采样层和一个卷积层,通过上采样层将细化的特征上采样到与目标图像相同的尺寸,卷积层输出理想图像与LRMS图像之间的残差,最后根据细节注入模型[14],使用跳跃连接将上采样的LRMS图像与卷积层的输出相连接得到融合图像。

2.5 鉴别器结构

本文鉴别器由5层全卷积神经网络构成,如图3b所示。卷积滤波器的尺寸均为3×3。网络前3层卷积步长设置为2,等同于池化运算用于提取特征,最后两个卷积层步长设置为1。除最后一层使用Sigmoid函数用于预测图像的真实性外,其余4层均使用LeakyReLu激活函数。

2.6 损失函数

本文网络的损失函数包括生成器损失和鉴别器损失两个部分。生成器损失函数表示为

LG=αLadv+βLcont

(11)

式中:Lcont为内容损失;α和β为平衡参数,用于平衡对抗损失和内容损失,实验中分别设置为1和100[18-19];Ladv表示生成器与鉴别器间的对抗损失,公式为

Ladv=

(12)

其中N表示训练样本数。

相比于L2损失容易造成融合图像产生模糊现象[13],L1损失则能较好地保持边缘细节信息[18-19]。因此,本文使用L1损失作为内容损失

(13)

式中‖·‖1表示L1范数。

鉴别器损失函数表示为

LD=

(14)

3 实验及结果分析

3.1 网络训练环境配置与参数设置

本文使用Tensorflow深度学习框架,在NVIDIA Quadro RTX 5000显卡上进行训练和测试。训练过程中使用Adam优化器,初始学习率为0.000 2,动量为0.5,批量尺寸设置为32。

3.2 实验数据集与评价指标

本文使用GF-2卫星和QB卫星获取的图像作为网络的训练集与测试集。GF-2卫星拍摄的PAN图像与LRMS图像的空间分辨率分别为0.8和3.2 m,QB卫星拍摄的PAN图像与LRMS图像的空间分辨率分别为0.6和2.4 m。对原PAN图像与LRMS图像进行裁剪,得到40 000对PAN图像和LRMS图像作为训练集。

定量评估采用5种常用的低分辨率评价指标和3种全分辨率评价指标:低分辨率评价指标包括光谱角映射(Γ)[28]、相关系数(T)、空间相关系数(Z)[29]、相对全局误差(Λ)[30]、平均通用图像质量指标(Θ)[31];全分辨率评价指标包括无参考质量指标(Δ)[32]以及QNR中评价光谱细节损失的指标(Dλ)和评价空间细节损失的指标(Ds)。

3.3 残差空间注意力模块数量的选择

考虑到不同数量的RSA模块会对网络的参数数量以及融合效果产生影响,本文在GF-2卫星数据集上对包含不同数量的RSA模块构成的网络进行实验,结果如图6所示,图中L表示RSA模块的数量。可以看出,不同的L对于指标T、Z和Θ影响较小,而对于指标Γ以及Λ则影响较大。当L=6时,所有的指标均接近于最优值。考虑到计算效率和模型参数之间的平衡,实验中设置RSA模块的数量L=6。

图6 不同数量RSA模块构成的网络在GF-2卫星数据集上的指标均值对比Fig.6 Comparison of index mean values of networks with different number of RSA modules on GF-2 satellite datasets

3.4 视觉评估

本文对GF-2号卫星图像和QB卫星图像分别进行低分辨率测试和全分辨率测试。由于真实的HRMS图像并不存在,所以在对图像进行低分辨率实验时遵循Wald协议[30],即将原始的PAN图像与LRMS图像均进行4倍的下采样,然后将原始的LRMS图像作为真实的HRMS图像。由于使用的卫星图像为不易直接显示的4通道(蓝、绿、红和近红外)图像,所以文中显示的图像都为3通道(红、绿、蓝)的真彩色图像。

(a)LRMS图像 (b)PAN图像 (c)SFIM[11]

(d)Wavelet[10] (e)IHS[8] (f)RED-cGAN[19]

(g)PSGAN[18] (h)本文算法 (i)理想图像图7 不同算法对GF-2图像的低分辨率全色锐化结果Fig.7 Results of low resolution pan-sharpening of GF-2 images by different algorithms

(a)LRMS图像 (b)PAN图像 (c)SFIM[11]

(d)Wavelet[10] (e)IHS[8] (f)RED-cGAN[19]

(g)PSGAN[18] (h)本文算法 (i)理想图像图8 不同算法对QB图像的低分辨率全色锐化结果Fig.8 Results of low resolution pan-sharpening of QB images by different algorithms

图7和图8是不同算法对GF-2卫星和QB卫星的低分辨率图像全色锐化结果。可以看出,在图7中SFIM[11]、Wavelet[10]和IHS[8]算法融合的图像偏白色,与真实的图像相比存在着光谱失真现象。另外,图7c和图7d出现严重伪影,造成不良的视觉效果。RED-cGAN[19]、PSGAN[18]以及本文算法融合的图像则能够保持与真实图像相似的光谱信息。但是,在放大区域中,与图7f和图7g相比,图7h中包含更多的建筑物缝隙细节,因此本文算法的融合结果可以保持更多的细节信息,同时减少了光谱失真。从图8可以看出:SFIM[11]、Wavelet[10]和IHS[8]算法保持的纹理细节信息接近于PAN图像,然而由于基于成分替代以及多分辨率的算法未能合理地向上采样的LRMS图像中注入空间细节信息,导致融合图像产生失真现象;RED-cGAN[19]、PSGAN[18]以及本文的算法则可以更好地保持光谱信息;另外,从图8f、8g和8h中的红色方框区域可以看出,本文算法可以保持更多的细节信息。

图9和图10是不同算法对GF-2卫星和QB卫星的全分辨率图像全色锐化结果。可以看出,图9c～9e表现出不同程度的光谱失真,其颜色偏暗,与上采样的LRMS图像光谱信息差距较大,图9f、9g、9h与上采样的LRMS图像具有相似的光谱信息,图9h的空间结构保持效果优于图9f和9g。在图10中的放大区域中,图10d和10e存在失真现象,这与在低分辨率下的融合结果一致。另外,图10c、10d、10g出现的伪影造成了不良的视觉效果,相比图10f,本文算法的融合结果具有良好的空间结构。综合可知,本文算法在GF-2卫星图像和QB卫星图像的全分辨率融合效果以及低分辨率融合效果都优于其他算法。

(a)LRMS图像 (b)PAN图像 (c)SFIM[11] (d)Wavelet[10]

(e)IHS[8] (f)RED-cGAN[19] (g)PSGAN[18] (h)本文算法图9 不同算法对GF-2图像的全分辨率全色锐化结果Fig.9 Results of full resolution pan-sharpening of GF-2 images by different algorithms

(a)LRMS图像 (b)PAN图像 (c)SFIM[11] (d)Wavelet[10]

(e)IHS[8] (f)RED-cGAN[19] (g)PSGAN[18] (h)本文算法图10 不同算法对QB图像的全分辨率全色锐化结果Fig.10 Results of full resolution pan-sharpening of QB images by different algorithms

3.5 定量评估

由于视觉评估受主观因素影响较大,因此本文对GF-2卫星数据和QB卫星数据实验结果进行了定量实验,结果如表1和表2所示。可以看出,对于低分辨率评价指标,基于深度学习的算法优于传统算法。由于Pan-RaGAN根据细节注入模型将学习到的细节注入到上采样的LRMS图像,因此本文算法的Γ获得了很大的提升;本文算法T较好,表明本文算法可以获得与理想图像更接近的效果。这与定性实验中的结果相符合,进一步说明了本文算法在低分辨率下测试结果的有效性。对于全分辨率参考评价指标,表1中本文算法在客观评价指标Ds上虽然没有取得最好的结果,但是从主观评价图9中可以看出,本文算法依然取得了良好的效果。在表2中,由于全分辨率评价指标将PAN图像和LRMS图像作为参考,而IHS[8]算法使用PAN图像替换LRMS图像的空间成分,使得融合后的图像具有与PAN图像相似的细节信息,因此IHS[8]算法获得了比本文算法更好的Dλ。

表1 不同算法在GF-2数据集上的定量比较

表2 不同算法在QB数据集上的定量比较

3.6 相对平均鉴别器与条件鉴别器

由于PSGAN使用条件鉴别器损失函数获得了良好的效果,因此本文在网络中分别使用条件鉴别器损失函数和相对平均鉴别器损失函数构成Pan-cGAN网络以及Pan-RaGAN网络,并在GF-2卫星数据集进行训练和测试,以验证相对平均鉴别器损失函数的有效性,实验结果如图11所示。可以看出,与Pan-cGAN的融合结果相比,本文算法的融合结果包含更多的细节信息。图11中黄色方框内,本文算法的结果更接近理想HRMS图像,而Pan-cGAN融合结果则出现空间细节模糊。

(a)Pan-cGAN (b)本文算法 (c)理想图像图11 使用相对平均鉴别器与条件鉴别器的全色锐化对比Fig.11 Contrast of pan-sharpening results between relative average discriminator and conditional discriminator

表3是使用相对平均鉴别器与条件鉴别器的全色锐化定量结果。可以看出,本文算法在低分辨率下的定量评价指标均优于Pan-cGAN的,进一步说明了相对平均鉴别器损失函数的有效性。事实上,当使用相对平均鉴别器时,生成器损失函数受到理想HRMS图像和生成HRMS图像的共同作用,但是在条件对抗网络中,生成器损失函数只受生成HRMS图像的影响。因此,通过相对平均鉴别器可以提高融合图像与理想的HRMS图像之间的相似性。

表3 使用相对平均鉴别器与条件鉴别器的全色锐化定量结果

4 结 论

本文提出一种用于全色锐化的相对平均生成对抗网络,与现有算法相比,本文算法在主客观评价上均取得了良好的结果,可获得包含更丰富细节信息和光谱信息的融合图像。本文结论如下。

(1)改进的密集块结构和空间注意力机制能够提高融合图像的空间分辨率,同时保持光谱信息。在QB数据集上,本文算法的Γ比PSGAN算法的小0.157 4,Δ比PSGAN算法的大0.020 6。

(2)在网络结构与参数相同的情况下,相对平均鉴别器损失函数与条件鉴别器损失函数相比,能更好地保持图像的细节信息。在GF-2数据集上,使用相对平均鉴别器损失函数的Γ和Λ比使用条件鉴别器损失函数的Γ和Λ分别小0.061和0.057 7。

(3)虽然本文算法在全色锐化中取得了良好效果,但仍然存在泛化性不强的问题。下一步将探讨深度学习算法与传统算法的结合,进一步提高算法的泛化能力。