中美标准中三种NEN型固定管板设计方法的比较

薛明德,李世玉,吴 坚,杨 旭

(1.清华大学 工程力学系，北京 100084；2.中国石化工程建设有限公司，北京 100101)

0 引言

自20世纪70年代清华大学黄克智院士对管壳式热交换器提出一套完整的管板分析方法，其后作为GB/T 151、JB 4732标准管板设计计算的规范方法以来，已经逐步为国内外同行所接受；此后，美国ASME、欧盟EN沿袭着同样的分析思路和类似的力学模型制定了管板设计规范。

目前，在我国工程界广泛应用的管壳式热交换器管板设计有三种方法：GB/T 151—2014《热交换器》[1]、JB 4732—1995《钢制压力容器—分析设计标准》[2](2005年确认)、美国ASME规范“ASME Section Ⅷ,Division 1”[3]。三种设计方法的基本原理都是将管板布管区简化为弹性基础上的当量削弱轴对称圆平板[4-7]，黄克智等[8]提出的中国方法(1978年获“全国科学大会奖”)与十多年以后SOLAR等[9]给出的美国方法之差别在于前者既考虑管板的弯曲;又考虑面内拉伸，而后者只考虑管板弯曲。JB 4732附录Ⅰ给出了我国管板应力分析的板壳理论解，是对于实际热交换器结构相对简化较少的分析方法，另两种方法在此基础上又作了更多的简化。为便于工程设计计算和应用，GB/T 151和ASME在此基本原理的基础上，都对管板边缘非布管区以及管板边缘与其他元件的连接条件进行了简化，同时还略去了管板面内拉伸变形与应力，只考虑管板弯曲。

在将带有换热管的规则排列多孔板简化为当量削弱轴对称圆平板计算时，需要引入管板的刚度削弱系数η和强度削弱系数μ，中国规范与美国ASME规范分析所采用的力学模型不同，造成最终计算得到管板最大应力不同，有时甚至会有较大的差别。

虽然这三种设计方法有类似的基本原理，但由于上述简化假定和削弱系数的区别，用三种不同方法对相同设计参数下、同一个管板进行计算，所得管板中的最大应力有时会差别很大。本文用上述不同方法，通过7个不同设计参数的NEN型固定式热交换器管板实例的计算结果，分析发生此问题的原因，探讨各种设计方法的适用条件。

1 7台NEN型固定式热交换器实例的管板最大应力计算结果及理论解的分析验证

表1列出7台NEN型固定式热交换器管板的计算实例，参数分别用文献[1-3]中三种不同设计方法计算得到。

表1 7台NEN型固定式热交换器实例基本设计参数和管板最大应力(MPa)

(续表1)

为了验证各种计算方法的可靠性，还对其中3台实例给出了用三维实体有限元计算得到的管板中的最大应力。对热交换器按以下方法建模：将其轴向中间横截面作为对称面，再取其1/12、沿0°和30°两个纵截面作为对称面,该3个对称面包围1/24的热交换器作为力学计算模型，以No.1算例为例，如图1所示。热交换器整体结构应力分析采用ANSYS 15.0 有限元分析软件中的 20节点三维实体单元Solid 186进行划分。为保证计算精度，在划分网格前对整体结构进行了合理细致地划分，保证网格全部是较为规则的六面体单元，对换热管沿壁厚方向划分为2层网格。模型总单元数为1 582 992，节点数8 198 863。

图1 NEN型固定式热交换器三维有限元网格

由于网格划分足够密，该三维实体有限元计算结果可以作为实际热交换器变形、应力分析的一种数值试验结果。由表1可知，3台热交换器实例(直径分别为1.07,3.55,6.76 m)分析的有限元计算结果都与JB 4732分析结果吻合较好；与ASME规范分析结果差别较大；仅当热交换器直径较小时，GB/T 151分析结果才与数值试验结果一致，其中算例No.7已经超出GB/T 151的适用范围，虽然算例No.5在国标GB/T 151的适用范围之内，但已经接近适用范围的极限。

图2对算例No.1热交换器给出了用JB 4732计算和有限元计算所得管板表面的应力分布曲线。结果显示：在管板布管区，理论解与数值试验解能够很好地符合；在管板布管区边缘与非布管区连接处，不出现理论解所显示的突变高应力；在与圆筒连接处的管板外沿，数值解计算得到的应力也小于理论解。其原因在于板壳理论解所建立的力学模型和几何形状复杂的实际结构之间应力分析不能完全吻合，应说明的是：此处“吻合”还不包含峰值应力。

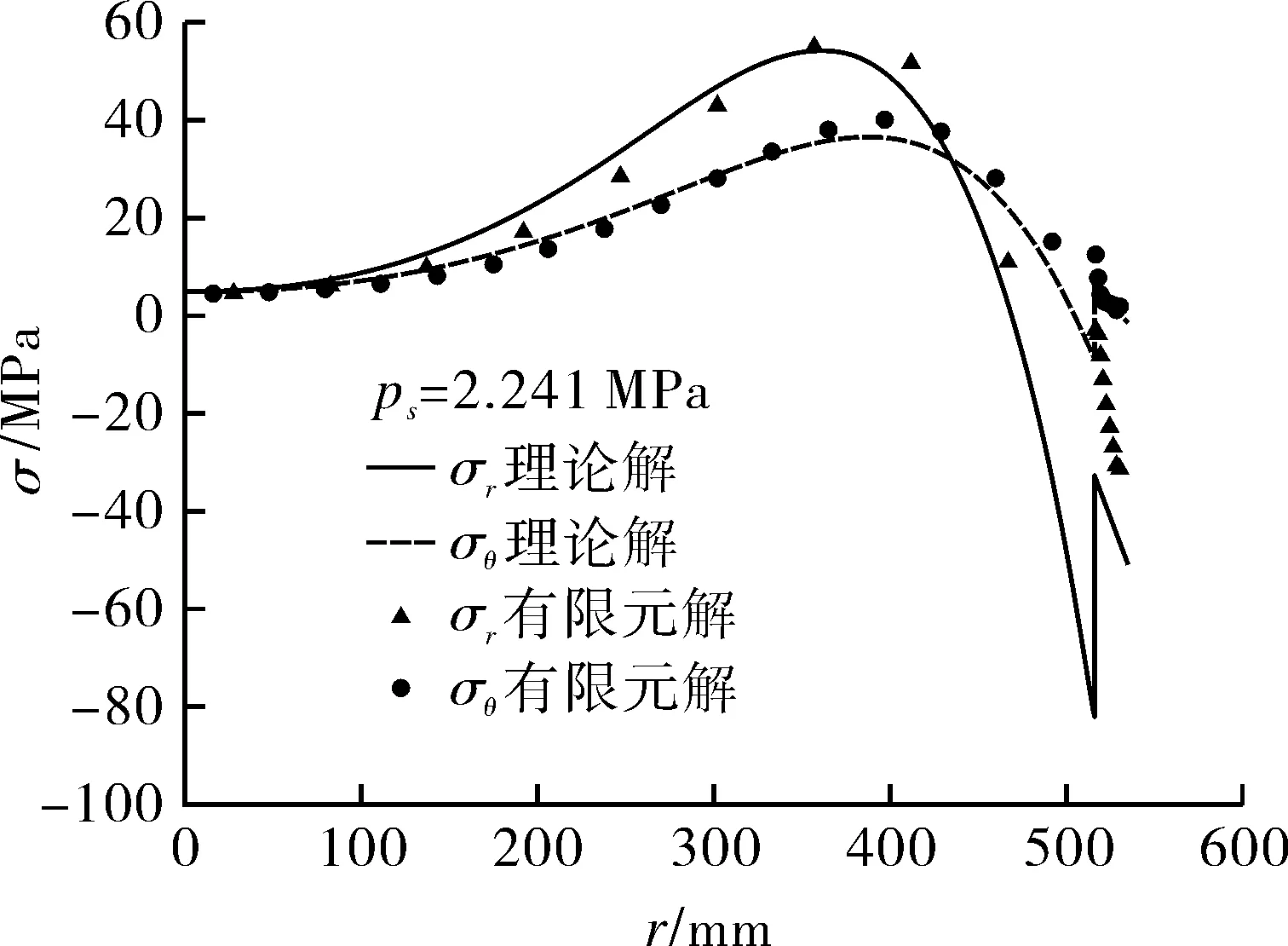
(a)ps作用下算例No.1管板管箱侧表面应力

JB 4732附录Ⅰ对于固定管板所建立的力学模型详见文献[2,8]，对于NEN型热交换器如图3所示。基本原理概述如下。

(1)管板布管区简化为轴对称均质当量圆平板，它同时承受弯曲和面内拉伸(分别按薄板弯曲和平面问题分析)，换热管束对两块管板的支承作用简化为均匀分布于管板布管区的弹性基础。在考虑当量板的拉伸和弯曲削弱系数时，必须同时计及管孔所带管子的作用[10-11]。

(2)管板布管区外缘通过轴对称圆环形弹性板在其上下表面分别与壳程圆筒和管箱圆筒(分别按薄壳理论分析)连接，连接内力素见图3；圆环形板(按薄板弯曲问题和平面问题理论分析)通过面内拉力与弯矩、横剪力传递给管板布管区拉伸和弯曲变形与应力。

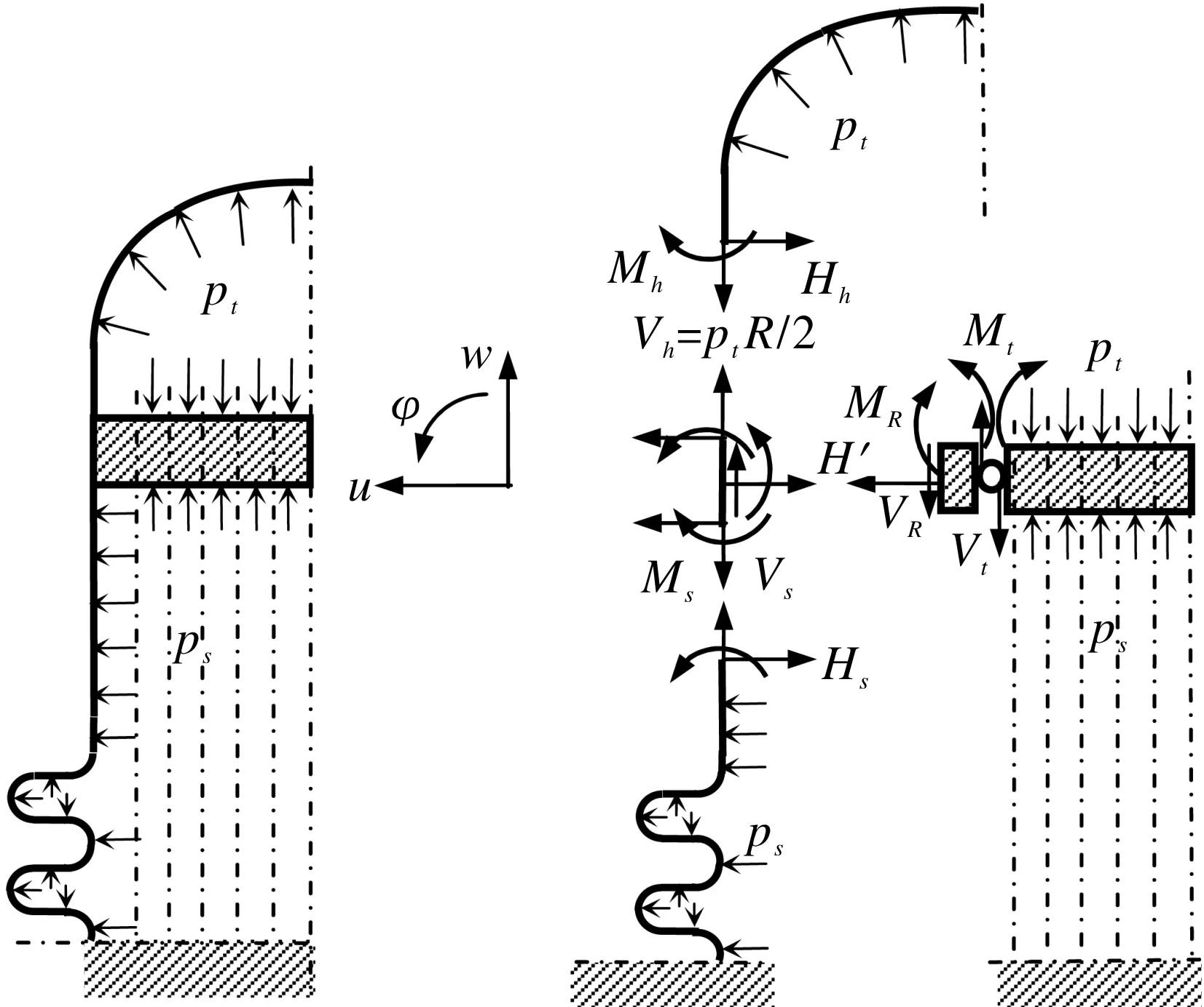
图3 不带法兰的固定式热交换器板壳理论解力学模型

理论解与数值试验结果在管板布管区的应力分布相吻合，说明“弹性基础上的轴对称均质当量圆板”这一基本力学模型是合理的，JB 4732所采用的管板削弱系数是符合实际的，此结论也被笔者以前的管板实测结果[12]所证实。

在管板边缘布管区与非布管区连接处，数值试验结果小于理论解，不出现理论解所得应力突然增大的情况，在文献[12]中，多个管板实测结果也显示同样的情况。产生这种现象的原因是将复杂形状的非布管区(见图1(a))简化为当量轴对称圆环形板的假定存在瑕疵。它虽然可以从总体刚度上反映非布管区对布管区变形的约束，但理论解中圆环形板(不计削弱系数)与开孔削弱当量圆板之间弯曲与拉伸刚度发生突变，造成二者连接处突然出现应力集中，在实际中并不存在。由于这种假定造成设计计算偏于保守，为简便定量计算，在目前规范[1-2]中仍然予以采用。

至于非布管区数值解的应力小于理论解的原因，是因为有限元建模时考虑了壳体与管板连接处有过渡圆角(见图1(b))，减小了应力集中，而理论解无法考虑的缘故。

2 对GB/T 151中NEN型固定式热交换器计算方法的分析

GB/T 151—2014《热交换器》对管壳式热交换器设计方法规定的适用范围(见文献[1]第1.5条)是Di≤4 000 mm，pDi≤2.7×104(MPa×mm)。表1给出前述7台热交换器实例用GB/T 151方法和JB 4732方法所得管板中最大径向应力的比较。其中，算例No.1～No.5满足GB/T 151的适用范围，算例No.6,No.7超出GB/T 151的适用范围，所有算例都满足k≤1的要求。

由表1可知，除算例No.4外，所有算例按JB 4732计算控制管板设计厚度的最大应力取值点都在管板布管区与非布管区交界的Rt处，算例No.2甚至在管板与壳体连接处，只有算例No.4最大应力发生在管板中心部位，这是因为其他算例的管子加强系数K值都很大的缘故。对于算例No.4，GB/T 151方法[1]和JB 4732方法[2]的计算结果相吻合，但对于其他算例两种计算结果都不能吻合。进一步观察发现，如果考虑到本文第2节所述：在管板布管区与非布管区交界的Rt处突然出现应力集中实际上并不存在的情况，进一步给出理论解在管板内部的最大应力，会发现对于算例No.1～No.3，如果不计及理论解所给Rt处的最大应力，剔除这些过于保守的结果，GB/T 151所给设计方法仍旧可以采用。

提出上述看法的理由是基于GB/T 151方法采用的力学模型避免了管板布管区与非布管区交界的Rt处突然出现应力集中这种不合理的现象。GB/T 151采用的力学模型[13-15]基于以下假设：当管板非布管区很窄时，对于管板布管区(简化为弹性基础板)的边界约束刚度主要由外缘的壳体提供，管板非布管区的刚度所起作用很小。所以可先根据遍布于整个管板范围(r≤R)的弹性基础板、直接连接外缘壳体，计算弹性基础板内的应力分布规律，再取r≤Rt处的应力值作为校核应力之一。

所以，对于直径与压力参数较小的NEN型固定式热交换器，如算例No.1～No.4，GB/T 151仍旧可以适用。而接近或超出GB/T 151设计方法适用范围的NEN型固定式热交换器，如算例No.5～No.7，GB/T 151所给设计结果安全裕度不足。其原因是GB/T 151方法采用的力学模型没有考虑管板上下边缘分别施加的横剪力Hh和Hs所引起的管板面内拉伸与附加弯曲变形，如图4所示。GB/T 151的力学模型假设与管板边缘连接的外部结构(对于NEN型固定式热交换器，只有管箱和壳程圆筒)没有面内沿径向的拉伸变形，只有弯曲与轴向变形，据此导出管板外缘的结构对于管板边缘的弹性约束刚度系数K～f，在此假定下K～f的计算只与外部结构参数有关，与外加载荷无关，使管板的分析计算得以简化。被GB/T 151力学模型所略去的管板边缘所作用的径向力如图4上方虚线所示。

图4 GB/T 151的力学模型

进一步分析可发现，当分别分析壳程压力工况或管程压力工况时，如果管板较厚，管板上下表面的径向拉力Hh或Hs不仅会引起管板面内拉伸力H′=Hs+Hh，还必将造成附加的管板弯矩Δ=(Hs-Hh)δp/2，其数值和相对管板边缘弯矩MR所增加的百分比见表2。此外，直径越大，壳体由于施加的压力载荷发生的径向位移和转角越大；这些情况都决定了GB/T 151所采用力学模型在大直径、高压力情况下，对管板应力分析会造成过大的偏差。

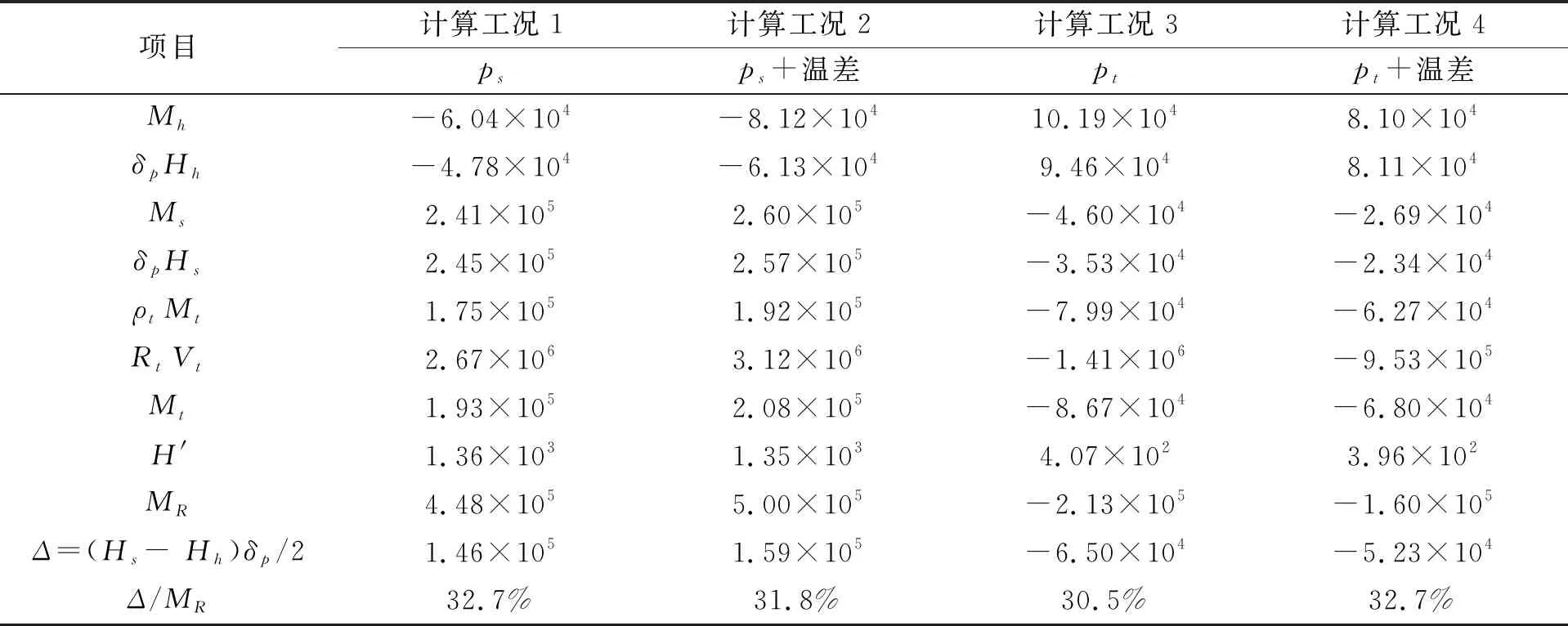
表2 管板边缘径向拉力所引起的附加弯矩(算例No.5反应器(板壳理论解))

表2以算例No.5反应器(Di=3 550 mm，δp=145.5 mm)为例，用文献[2]的分析设计法给出图3所示力学模型中管板边缘的内力素，进一步的分析可知，此时管板边缘径向拉力所引起的附加弯矩约占MR的30%以上，面内径向拉力H′引起的面内薄膜拉应力与MR引起的弯曲应力之比略小于10%。

3 对ASME规范中NEN型固定管板计算方法的分析

由表1可知，对于同一台NEN型固定管板，用ASME方法计算得到的绝大多数管板应力大于甚至远大于用两种中国规范[1-2]计算所得的应力，其主要原因在于所采用的力学模型不同、管板布管区的削弱系数不同；而3个三维实体有限元计算所得管板应力与理论解很接近。在相同载荷工况下按照板壳理论解[2]与有限元解计算所得的管板应力的比较见图2；结果显示，在管板布管区，二者能够很好地符合，在其外缘与非布管区连接处，有限元解得不到理论解所显示的高应力集中，如前文所述，这是由于理论解采用力学模型与实际结构的偏差所致，此问题在ASME方法所得计算结果中也同样存在。

ASME方法所采用的力学模型可参考文献[16-18]。与文献[2]相比，其区别在于：将管板边缘非布管区简化为一个横截面不变形的轴对称弹性圆环而不是圆环形板，它的矩形横截面只能绕其形心发生转动，不能发生径向拉伸或弯曲变形，与壳程和管箱圆筒的连接处，以此转角φR，φR在管板壳程侧或管程侧表面对应的径向位移±φRδp/2与壳程或管箱圆筒边缘的转角和径向位移满足变形协调条件。此简化假定的问题在于：当管板较薄时，管板非布管区的径向位移和弯曲变形很难被略去，同时如果壳程圆筒和管箱圆筒较薄时，其在ps或pt作用下会发生较大的径向膨胀薄膜位移，此时强令其边缘与圆环转动引起的径向位移协调一致，相当于附加了偏于刚性的边缘约束，这将增加管板与圆筒连接的边缘应力。将算例No.1(ASME PTB-4—2013)的网格图1(c)中Ⅳ-Ⅳ剖面的横截面作图，见图5；该图给出由有限元分析所得算例No.1在壳程压力作用下的管板边缘变形，此时由于弹性基础的作用，管板布管区与非布管区的交界处(r=Rt)边缘转角非常小，而壳程圆筒与管板连接处在压力作用下必定会发生较大的转角，表明ASME规范将管板边缘非布管区简化为刚性圆环的假定不符合实际。为与变形前横截面进行比较，图中变形后横截面是将其平移、放大200倍后得到的。

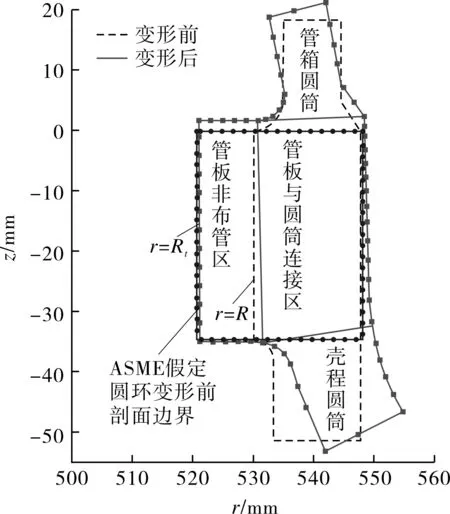
图5 算例No.1横截面变形前后的比较

表3列出了ASME Ⅷ-1，UHX篇 和JB 4732标准关于管板计算过程的详细比较，结合表1给出的多个算例的分析比较，可以看出ASME规范的不足之处，如不布管区的刚性圆环假定、削弱系数的确定、不计管板面内拉伸等，最终导致了管板计算应力的过大偏差。

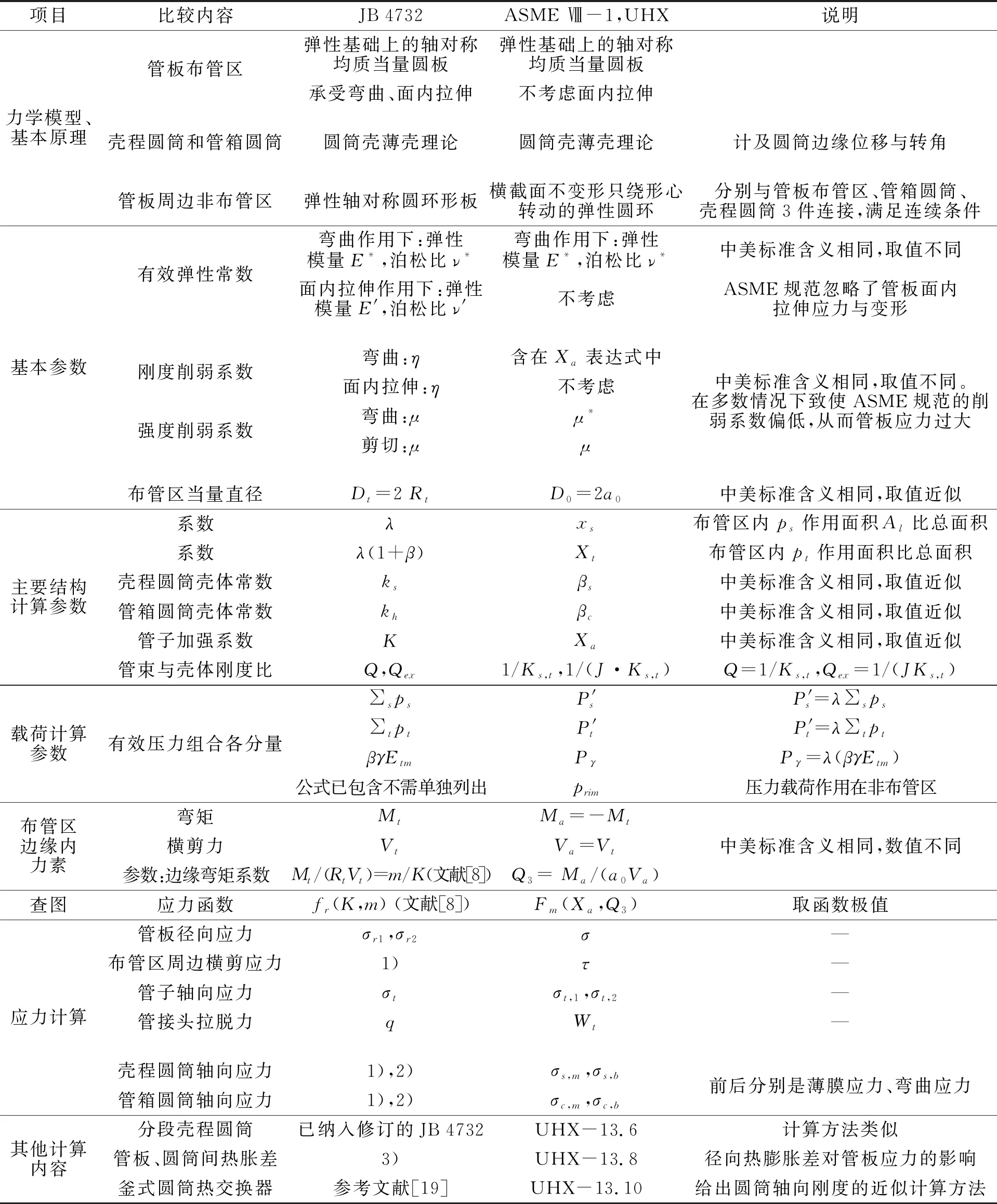
表3 中、美标准中管板计算方法比较(NEN型固定管板式热交换器)

ASME方法与中国规范[1-2]的区别还在于所采用的削弱系数不同，中国规范依据带管子的孔板力学模型[10-11]分析，说明换热管对于孔板有重要的加强作用，其力学模型见图6，再根据常用的布管和换热管尺寸，采用经验数μ=η=0.4；而ASME方法采用削弱系数所依据的力学模型是无管的孔板力学模型，再将胀接部分管子壁厚经折算计入管孔内壁，将孔直径由d缩减为d*，见图6(c)；绝大多数情况下计算得到的强度削弱系数μ*数值较小，造成计算所得管板应力偏大，表1给出了对7个算例ASME方法所采用的强度削弱系数μ*。表1中还给出若将ASME方法改用μ*=0.4时，对应计算得到的管板应力值，此时部分计算结果与理论解接近；但如果管板和与其相连接的圆筒厚度很薄时，仍会产生很大的误差，如算例No.2,No.3所示，这时管板边缘处力学模型的简化影响较大。

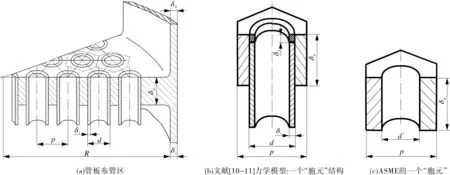
图6 将规则排列的多孔管板折算为当量轴对称圆板求削弱系数的力学模型

将图6(a)所示规则排列的多孔板折算为无孔的削弱当量均质板的过程为：认为多孔板是由无数完全相同的“胞元”按照一定的规律(如正方形排列或三角形排列)固结而成的。取出其中一个“胞元”进行分析，列出它所满足的平板弯曲或平面问题的微分方程，在“胞元”孔板外边界(正方形或六角形)上给定这个“胞元”与相邻“胞元”所必须满足的连续条件，并且给出所施加的弯矩、扭矩，或面内拉力、切力；解此偏微分方程的边值问题，就可以得到这个“胞元”的变形和应力，从而得到当量均质板的削弱系数。

笔者在早期的热交换器管板应力测定[8，12]过程中，发现即使对于换热管与管板只有焊接接头连接时，按照孔间带效率(p-d)/p作为当量板的强度削弱系数,也将得到过大的应力，与实测结果不符。所以，文献[10-11]为得到更符合实际的削弱系数，采用了如图6(b)所示的“胞元”模型。该“胞元”是由孔板单元、换热管和连接二者的圆环构成的结构单元，圆环的高度δ1为换热管与板孔之间固结的长度(焊接接头深度或胀接长度，称为“连接高度”)。该“胞元”的数学描述为板的弯曲偏微分方程、平面问题偏微分方程、圆柱壳偏微分方程和圆环偏微分方程之联立的偏微分方程组；在“胞元”孔板外边界上给定的连续条件与前相同，分别加弯曲外力得到当量板弯曲削弱系数，加面内外力得到当量板拉伸削弱系数。

按照上述力学模型计算，可得到当量板的削弱系数与管板的各种结构参数之间的关系[10-11]，图7[10]给出他们与换热管和孔板之间“连接高度”δ1的关系算例之一(图中δ为板的厚度)。该典型算例中d=25 mm,δt=2.5 mm,p=32 mm。若按照简单的孔板模型(见图6(c))，换热管和孔板为焊接连接，不考虑换热管的加强作用，取μ°=(p-d)/p=0.218 75；如果换热管和孔板为焊接加全胀接,取μ·=(p-d+2δt)=0.375；但是由图7可看出，强度削弱系数约等于0.3～0.55，超过简单的孔板模型所给数值；说明换热管对孔板的加强作用远超过单纯将其厚度计入孔内径的值。

图7 当量板弯曲削弱系数与“连接高度”的关系

4 结论

(1)JB 4732—1995(2005年确认)是根据板壳理论对于实际热交换器结构作出的详细、完整的(相对简化较少的)分析方法，针对本文讨论的NEN型固定式管板，理论解与有限元分析结果有较好的吻合。

(2)GB/T 151和ASME规范在上述基本原理和详细分析的基础上，对管板边缘非布管区以及管板边缘与其他元件的连接条件进行了简化；同时还略去了管板面内拉伸变形与应力，只考虑管板弯曲。因此在一定条件下会导致难以接受的过大计算应力偏差。

(3)现行GB/T 151的适用直径参数范围是DN≤4 000 mm，在低参数范围内，GB/T 151的管板计算结果接近有限元的分析结果，能够满足工程设计的需要。对于直径接近或超过4 m的高参数热交换器，GB/T 151的计算方法大大低估了管板的计算应力。

(4)在大多数情况下，ASME Ⅷ-1方法会给出过大管板的计算应力。其原因除结论(2)所述的简化、省略外，主要是因为它所取的管板强度削弱系数μ*是来自于不符合实际情况的管子管板接头的力学模型，多数情况下大大低估了管子对管板的加强作用[10-11]。

致谢:全国锅炉压力容器标准化技术委员会设计计算方法专业委员会对本课题研究给予了大力支持，特此表示感谢。