2205双相不锈钢氢致开裂行为的试验分析与模型预测

陶 平，赵晨宇，巩建鸣

(1.南京工业大学 机械与动力工程学院，南京 211816；2.江苏省极端承压装备设计与制造重点实验室，南京 211816)

0 引言

双相不锈钢(Duplex stainless steel,DSS)综合了铁素体不锈钢抗离子腐蚀、高强度的特性,以及奥氏体不锈钢优良韧性和易焊接的优点，广泛应用于酸性石油天然气的开采设备中[1-3]。尽管DSS拥有良好的抗氯离子腐蚀性能，但是在含电解质(如海水、淡水及土壤等)的环境中仍会对其采用阴极保护技术(Cathodic protection，CP)，以避免或减缓其他形式的腐蚀[4-5]。研究表明，采用CP方法后，会在阴极产生析氢反应。 析出的氢原子通过吸附、扩散和溶解进入到材料内部，导致DSS发生氢致开裂(Hydrogen assisted cracking,HAC)[6-8]。通常，氢需要一定的时间向应力集中区(如缺口、夹杂处)扩散并富集，当富集的氢浓度达到临界值时，使裂纹萌生,并随着氢的进一步富集,裂纹迅速扩展，材料发生断裂。由于氢的扩散需要时间，HAC表现出时间上的延迟[9-10]。HAC通常不发生显著的塑性变形，也没有明显的征兆，危害性极大。对氢环境中使用的金属结构，如何预测和判断其是否会发生氢致开裂在工程上具有很大挑战性，备受关注。评价金属的HAC，通常采用缺口或预裂纹试样，施加恒应力或恒应力强度因子，随时间的增加，氢会向缺口或裂纹尖端高应力区扩散并富集，引起裂纹的萌生、扩展，直至试样断裂[11-13]。目前，对双相材料HAC的研究还不多见，仍需完善。

近年来内聚力模型(Cohesive zone model,CZM)被广泛应用于模拟裂纹的萌生与扩展[14]。SEREBRINSKY等[15]、LIANG等[16]和OLDEN等[11，17]将氢浓度相关的CZM用于模拟氢致裂纹萌生与扩展以及氢致应力腐蚀开裂等，取得了显著进展。CZM的实质是一种表征原子或分子间键合力的简化模型，基于氢致键合力降低理论(Hydrogen enhanced decohesion,HEDE)，通过引入氢对CZM本构关系的定量影响,SEREBRINSKY等[15]实现了对钢氢致裂纹形核与扩展的数值模拟，考察了强度、氢浓度等因素对断裂的影响，模拟结果与试验现象基本吻合。LIANG等[16]则将CZM(HEDE)与氢促进局部变形理论(Hydrogen enhanced local plasticity,HELP)结合起来,研究了Alloy 690合金析出相与基体界面孔洞形核与扩展问题，比较了两种理论对孔洞形核应力与应变的影响。OLDEN等[11，17]基于氢相关的CZM,预测了25%Cr双相不锈钢缺口拉伸平面应变试样在海水环境动态充氢下的氢致裂纹起裂过程，并与试验结果进行了比较。王艳飞等[18-19]开展了AISI 4315高强钢圆柱缺口试样在预充氢后恒载荷拉伸的滞后断裂有限元模拟，并考察了应力集中系数、初始氢浓度水平及拉伸载荷水平等因素的影响。目前，针对DSS的研究，含双相组织的内聚力模型还未见报道。

基于此，本文以海洋石油天然气开采平台和输送管道常用的2205双相不锈钢为研究对象，研究微观组织形态对2205双相不锈钢氢致裂纹萌生和分布的影响；并基于氢影响的内聚力理论，对双相不锈钢的氢致开裂现象进行有限元模拟分析，完善并发展考虑微观组织的内聚力有限元分析模型，以预测氢致裂纹起裂时间和起裂位置。

1 材料与方法

1.1 试验内容与方法

试验材料选用OUTOKUMPU公司提供的2205双相不锈钢钢板，厚度为4 mm，化学成分见表1。

表1 2205双相不锈钢化学成分

钢板的最终热处理工艺为1 100 ℃固溶处理后水淬，材料的三维微观组织见图1(a)，其中奥氏体相体积分数为54%。可以看出，在轧制作用下，微观组织中的相组织并不均匀，横向组织中晶粒尺寸为20～200 μm(见图1(b))，纵向(轧制方向)组织晶粒尺寸为10～40 μm(见图1(c))。

图1 2205双相不锈钢的微观组织

恒载荷氢致开裂电化学充氢装置如图2所示，试样选用单边缺口试样，如图3所示，一组沿轧制方向；另一组垂直于轧制方向。试验前依次用400#～2 000#砂纸进行打磨抛光，再用电解方法进行表面抛光，去除机械打磨引起的残余应力。试样抛光后，在酒精和丙酮混合溶液中进行超声波清洗，烘干备用。试验时，先将杠杆调平衡，将试样固定于充氢电解池中，并固定于加载装置底部，然后采用销连接将试样上端固定于加载装置进行砝码加载，加入充氢溶液(0.5 mol/L H2SO4+1 g/L CH4N2S)，接通电源进行充氢试验。此处，试样加载的应力为最小横截面上的平均应力σn。试验采用远程视频监控并定时检查，每隔12 h更换充氢溶液。

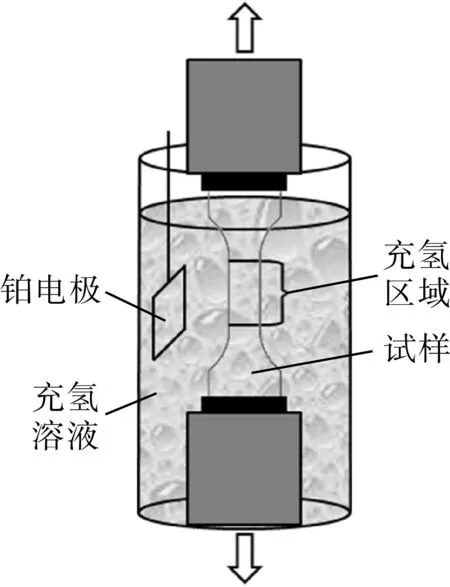
图2 恒载荷氢致开裂电化学充氢装置

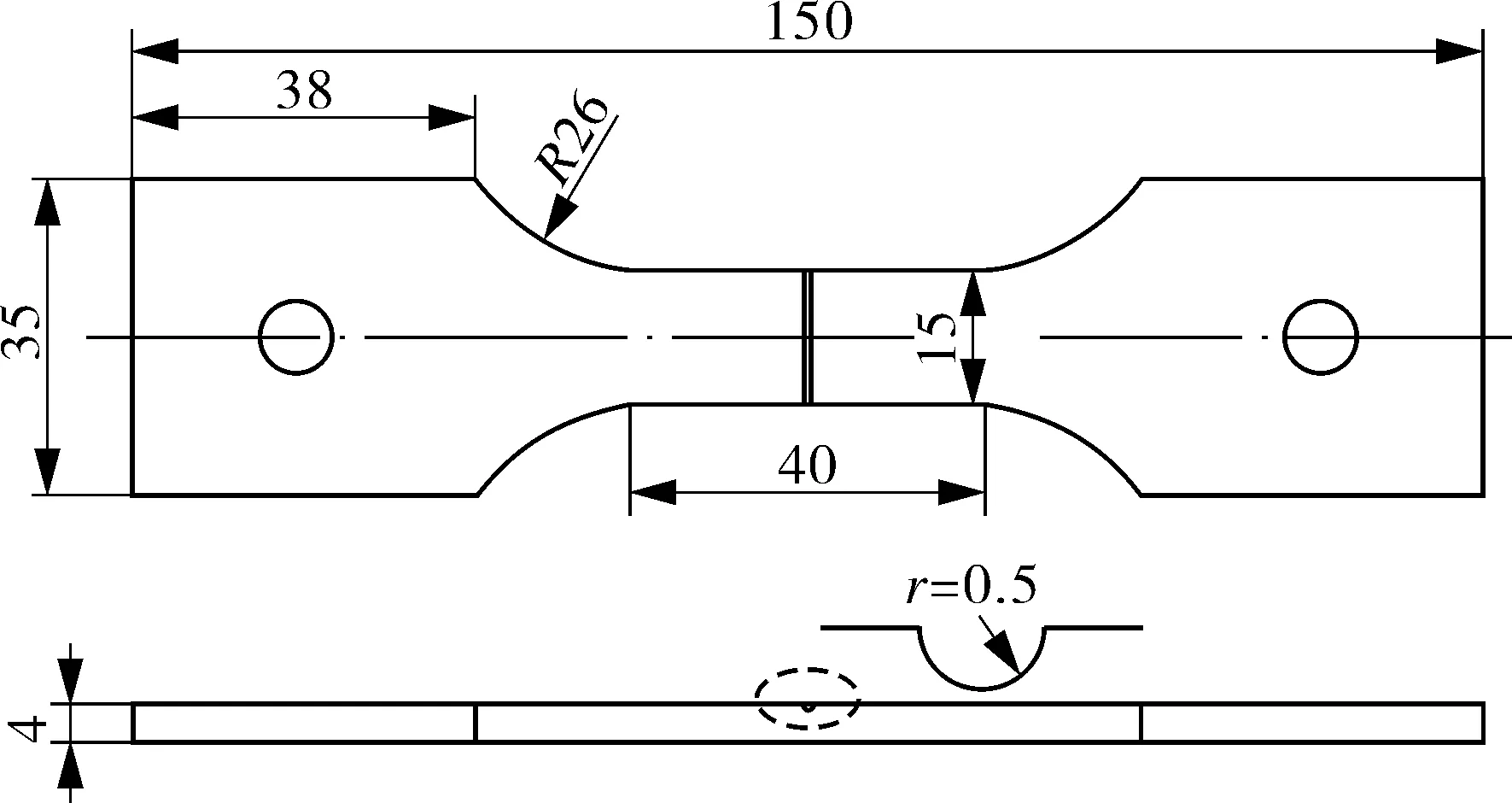
图3 单边缺口试样结构尺寸示意

1.2 基本理论

1.2.1 内聚力理论与氢浓度相关的TSL准则

内聚力理论假定裂纹尖端为一很小的内聚力区，内聚区由两裂纹界面组成，界面上有内聚力σ，σ和两个裂纹面的相对位移δ之间的关系σ(δ)构成内聚区的本构关系，称为牵引-分离准则(Traction-separation law,TSL)，通过TSL关系，实现对裂纹尖端的力学描述。有限元分析中，内聚力通常采用一层厚度为零或厚度接近于零的内聚力单元表示，内聚力单元可以灵活地嵌入到普通的网格单元中，单元的上下表面与相邻单元连接，外力引起的材料损伤限制在内聚力单元中，周围单元不受影响。通过定义内聚力单元的TSL本构关系，可以实现内聚力单元在外载作用下的损伤开始与演化。对金属材料，其TSL 较为复杂也难于通过试验获得，通常采用简单函数来近似描述TSL。

从能量的角度，裂纹扩展需要克服内聚力做功，大小即为TSL曲线所包围的面积，称为材料的内聚能Γc。由断裂力学理论可知,Γc可与材料的临界能量释放率Gc等效，可以表示为[12，20]：

(1)

式中,Kc为断裂韧性；E为弹性模量；υ为泊松比。

TSL可由σc,δc和Gc三个参数中的任意两个确定。SEREBRINSKY等[15]假定氢对临界能量释放率Gc的影响与氢对材料表面能γ的影响满足同样的关系。对于Fe/H系统，JIANG等[21]通过第一性原理计算得到H对Fe表面能的影响,可表示为：

Gc(θ)=(1-1.0467θ+0.1687θ2)Gc(0)

(2)

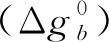
(3)

式中,R为气体常数，R=8.314 J·mol/K；T为温度，K。

问题是促进学生思维能力发展的有效途径，孔子曾说“不愤不启，不悱不发”，在学生解决问题的时候发现新的问题，通过一些预设和非预设的问题促进学生的学习主动性，培养学生的学科核心素养，提高教学效率.如何设计出有效的问题是关乎物理教学成败的关键，也是值得每一位物理教师进行探究的问题.下面就如何在高中物理课堂设计问题进行论述：

基于H-Al系统的计算表明，氢对临界张开位移(δc)的影响较小[22]，故通常假定δc为常数。因此，可得：

σc(θ)=(1-1.0467θ+0.1687θ2)σc(0)

(4)

式中,σc(θ)，σc(0)分别为含氢和不含氢时材料的内聚力强度，一般为2～6倍σy[23](σy为材料的屈服强度)。

线性TSL因为形式简单被经常使用，表示为：

(5)

图4示出不同氢覆盖率下的线性TSL，在初始阶段为刚性，不适于有限元计算，因此需要对线性TSL进行修正，采用有限初始刚度，即当单元张开位移超过临界值(δ0)时，单元才开始损伤。为保证修正前后TSL本身及其所围面积的变化较小，要求δ0要远小于δc，一般取δ0=10-7mm。

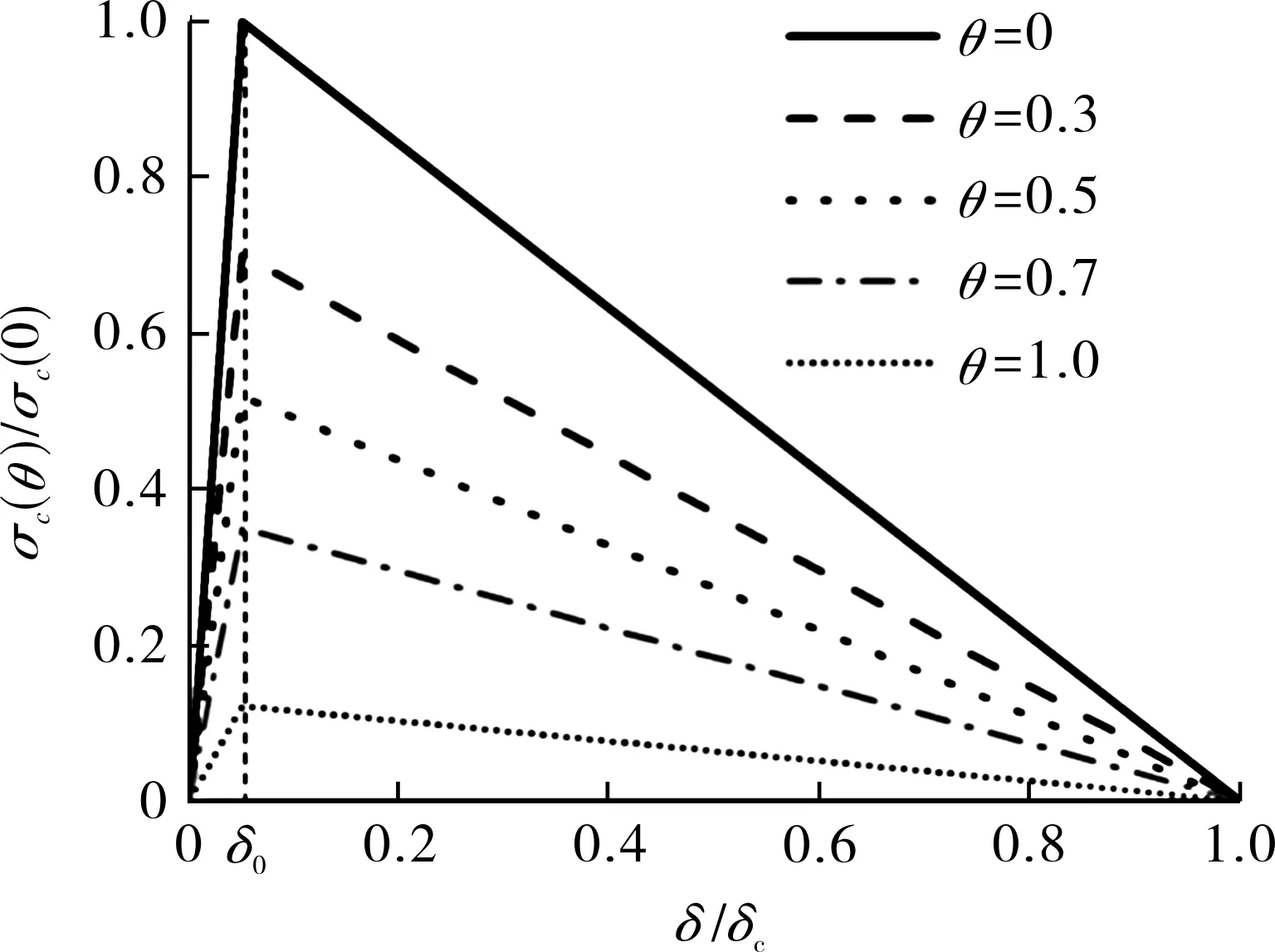
图4 氢浓度相关的线性TSL准则

1.2.2 应力诱导氢扩散理论

根据传质理论，由化学势梯度引起的氢扩散本构方程为：

(6)

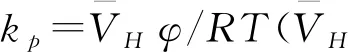
φ=C/s

(7)

归一化浓度φ的定义，保证了扩散过程在相界面上保持连续。将上式代入质量守恒方程，并替换浓度C为归一化浓度φ：

(8)

从而可得到应力驱动扩散的瞬态氢扩散控制方程为：

(9)

1.2.3 氢致开裂有限元模型

有限元模型的几何尺寸、边界条件和网格划分如图5所示。

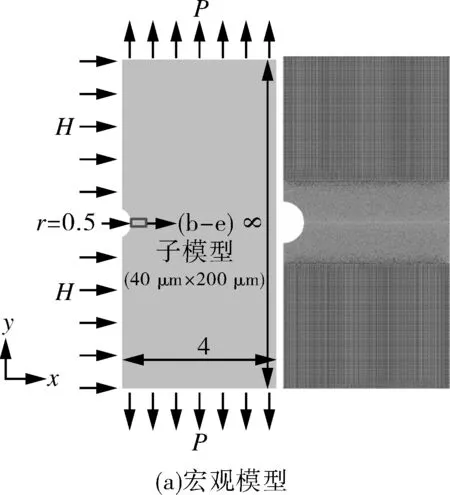
图5 含双相组织的有限元模型

模型分为宏观全局模型和微观子模型。全局模型的尺寸为4 mm×8 mm，子模型的尺寸为400 μm×200 μm。为了考察不同相晶粒形态分布的影响，采用代表性单元方法随机生成了4种含不同奥氏体相尺寸的双相组织子模型(5 μm×5 μm,10 μm×10 μm,10 μm×30 μm,30 μm×10 μm)，其中奥氏体相的体积分数都为54%，即与试验材料相体积分数一致。子模型的使用方法参照ABAQUS帮助文档Sub-modeling模块[24]，当全局模型计算结束后，子模型的边界条件直接从全局模型中获得。内聚力区沿x轴方向排布在缺口中间位置，单位内聚力单元尺寸为0.2 μm× 0.2 μm，约为2205双相不锈钢最小晶粒尺寸的1/10。全局模型与子模型分别划分270 000和53 000个单元。

分析过程采用如图6所示的顺序耦合方法。第1步，弹塑性应力分析，获得恒载荷作用下的应力场；然后将所得的静水压力场作为氢扩散的初始条件，进行第2步给定时间下的应力诱导氢扩散计算；再将所得的瞬态氢浓度作为预定义场进行第3步含有内聚力单元的恒载荷拉伸断裂计算，失效单元的位置即认为是裂纹萌生的位置，对应的扩散时间为发生断裂的时间。通常认为氢致裂纹一旦萌生后，即会迅速扩展、直至完全断裂，因此计算得到的裂纹萌生时间，可以保守作为发生氢致断裂的时间。氢扩散分析步、静应力分析步与内聚力分析步分别采用DC2D4，CPE4R，COH2D4的单元属性。模型使用的相关材料参数见表2。

表2 有限元模型中的相关参数

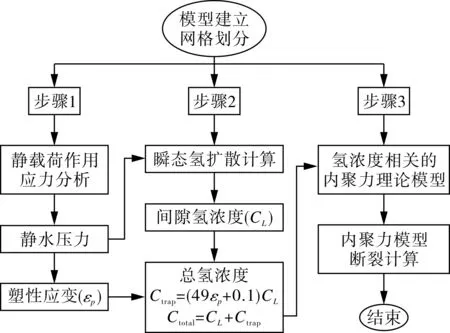
图6 顺序耦合内聚力有限元计算流程

2 结果与讨论

2.1 试验结果

图7示出单边缺口试样在横向和纵向两个方向施加拉伸缺口应力σn=0.9σy(σy为屈服强度)、充氢168 h 后，试样附近缺口裂纹分布。可以看出，橫向试样中的氢致裂纹比纵向试样中的裂纹更加明显。橫向试样中组织的排布更接近并联状态，而纵向试样中的组织排布更接近串联状态，串联状态的试样中的氢浓度比横向试样更低，因此裂纹扩展的总体平均长度更短。

图7 氢致裂纹在单边缺口试样中的分布 200×

图8示出裂纹分布的局部放大。

图8 氢致裂纹在单边缺口试样中的分布 500×

从图8可以看出，在缺口根部分布着明显的氢致裂纹，裂纹的方向与受载拉伸方向近似垂直。在主裂纹的裂尖处，可以观察到裂纹优先在铁素体相中萌生和扩展。随充氢时间的增加，当裂纹扩展穿过铁素体遇到奥氏体晶粒时，奥氏体相晶粒会阻碍裂纹的扩展，裂纹扩展速度降低，扩展的方向会一定程度上发生旋转。这种铁素体相和奥氏体相中氢致裂纹扩展的现象与文献[17，25]报道的结果一致；同时这些结果也证明了静水压力梯度对氢致裂纹萌生的影响。研究表明，氢致裂纹萌生的位置一般出现在静水压力梯度值较高的区域(距离缺口一定深度)，随时间增加，微小裂纹合并为更大的裂纹，导致材料的逐步开裂[26-27]。此外，裂纹扩展还存在另一种可能，即刚开始裂纹萌生在奥氏体相晶粒两侧的铁素体相中，由于受到拉伸载荷，尽管奥氏体相晶粒内浓度较低，但仍会被拉断。

2.2 模型预测结果

图9(a)(b)示出全局宏观模型在168 h时，在不同应力与90%屈服缺口应力(σn)下，不同扩散时间的氢浓度云图，表观氢扩散系数DDSS=1.0×10-12m2/s；图9(c)(d)示出了缺口沿扩散深度方向(x方向)的氢浓度分布。可以看出，在静水压力的作用下，氢浓度的峰值出现在缺口尖端一定距离位置区；随应力的增加，可扩散氢的浓度(CL)逐渐增加。相关的试验研究[28-29]也证实了在高静水压力梯度区氢浓度的增加。陷阱氢的浓度Ctrap由塑性应变εp计算获得，即Ctrap=(49.0εp+0.1)CL[30]。

图9 宏观模型氢浓度预测结果

图10示出子模型在氢扩散168 h后，施加应力与未施加应力状态下氢浓度与归一化氢浓度分布云图。由于铁素体相与奥氏体相的溶解度数值上差异较大，从氢浓度的角度很难直接对比。此处从归一化浓度φ的角度，分析了铁素体相和奥氏体相中氢扩散与分布情况的差异。

图10 微观模型(10 μm×10 μm)中预测的氢浓度与归一化氢浓度

图11示出了在无应力与90%屈服缺口应力的情况下归一化氢浓度分布。其中，曲线波动的位置为奥氏体相晶粒的区域，由于氢在奥氏体相中扩散较慢，需要更长时间才能达到饱和状态，导致在相同时间下的归一化氢浓度低于铁素体相。奥氏体相的细化程度越高，模型的表观扩散系数越低，平均氢浓度就越低，最小平均归一化氢浓度出现在5 μm× 5 μm 的模型中。这与CHOU等[31]的试验研究结果一致，当奥氏体相晶粒尺寸从12.58 μm 降低到7.42 μm 时，DSS的表观扩散系数由 4.78×10-14m2/s降为3.58×10-14m2/s。此外，当奥氏体相晶粒尺寸在垂直于氢扩散方向(y方向)延伸时，模型(10 μm× 30 μm)的平均氢浓度也降低了。根据GESNOUIN等[32]的假设，10 μm× 30 μm 的模型更接近于串联耦合，此情况下，奥氏体相对氢扩散的阻碍更大，氢陷阱作用更明显，导致整体氢扩散速度降低。

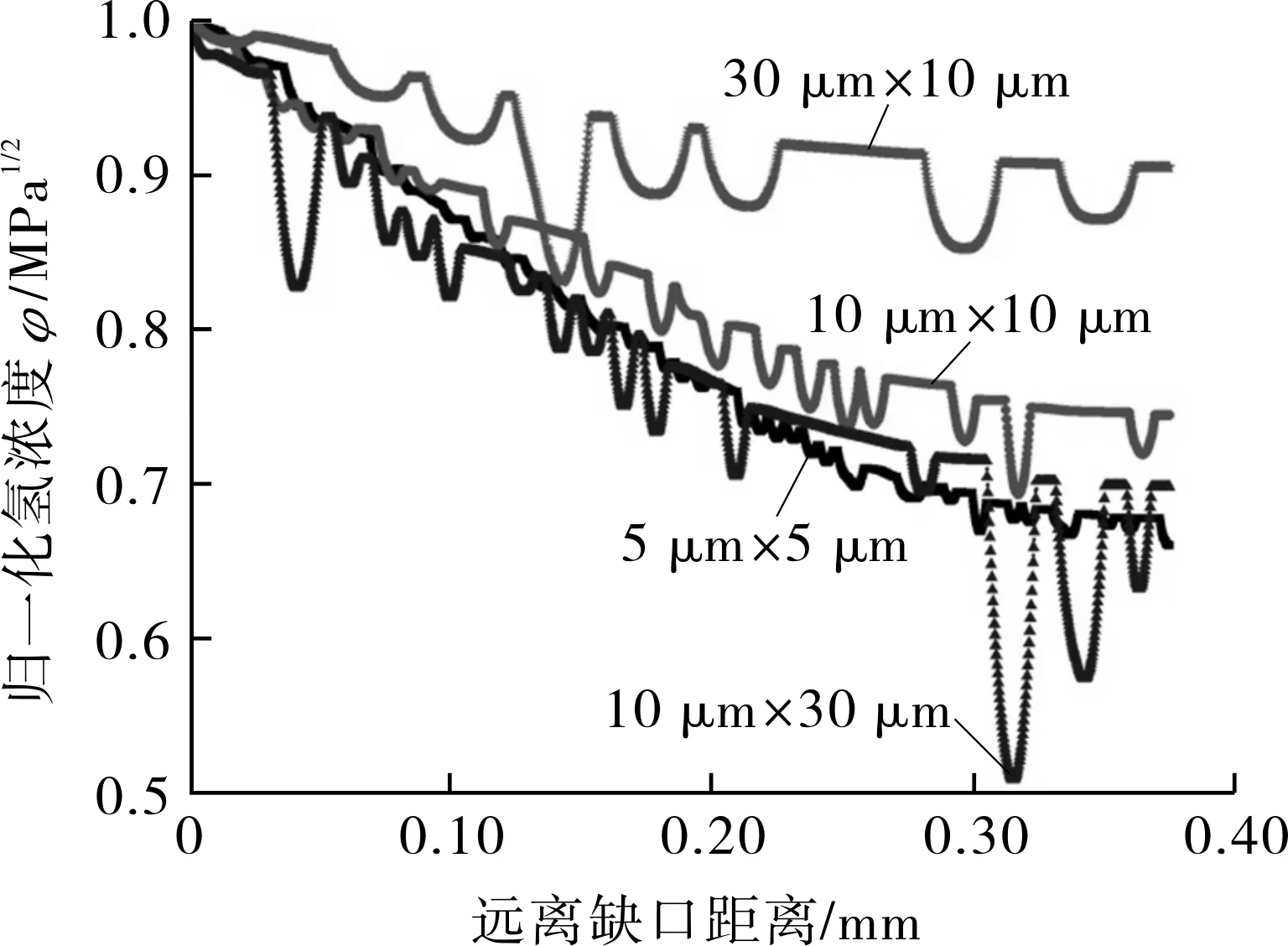
(a)无应力

图12示出4种含不同奥氏体相尺寸子模型预测的氢致裂纹分布。在静应力分析时，缺口尖端局部区还显示出现了局部的塑性区。为了考虑塑性变形对模型总氢浓度的影响，采用经验方程Ctotal=(49εp+1.1)CL对总氢浓度进行了计算(其中，εp为塑性应变，CL为晶格中的氢浓度)。将计算得到的总氢浓度作为内聚力计算分析步的初始条件。通过对比发现，更加细化的奥氏体相晶粒尺寸可以在一定程度上抑制氢致裂纹的长度，这与上述氢扩散的行为一致。因为较小的奥氏体相使得氢在铁素体相中的扩散路径更加不连续，降低整体氢扩散速度。当奥氏体相晶粒延伸时，裂纹的长度也会减小。因为此情况下，氢扩散进入到奥氏体相中达到饱和的时间更长，而相邻铁素体相在达到临界氢浓度则会出现氢致裂纹，裂纹的不连续性更加明显。

(a)奥氏体相尺寸5 μm×5 μm

3 结论

(1)横向组织单边缺口试样中的氢致裂纹比纵向组织试样中的裂纹更加明显，这是因为横向试样中组织的排布更接近并联状态，而纵向试样中的组织排布更接近串联状态。串联状态的试样中的氢浓度比横向试样更低，裂纹扩展的总体平均长度更短。

(2)基于氢浓度相关的内聚力理论，建立了含双相组织的氢致开裂预测模型，对充氢的双相不锈钢拉伸试样在恒载荷下的氢致裂纹萌生与扩展进行了计算。与无应力状态下的氢扩散相比，应力驱动氢扩散明显提高了模型中的氢浓度，且最大氢浓度的位置从缺口根部转移到与缺口的一定距离处。

(3)奥氏体相的细化程度越高，模型的表观扩散系数越低，平均氢浓度就越低，一定程度上抑制氢致裂纹的长度。因为较小的奥氏体相使得氢在铁素体相中的扩散路径更加不连续，降低整体氢扩散速度。当奥氏体相晶粒延伸时，裂纹的长度也会减小。此情况下，氢扩散进入到奥氏体相中达到饱和的时间更长，而相邻铁素体相在达到临界氢浓度则会出现氢致裂纹，裂纹的不连续性更加明显。