应用题中利用画图的策略,发展学生的数学思维
■福建省南平市政和县石屯中心小学 倪建毅
(邱瑞玲)
在小学数学应用题学习中,画图策略是一项学生必须重视并加以掌握的技巧。一方面,小学生的想象力丰富、逻辑能力不足,利用画图可以将抽象的问题具体化、直观化,达到“四两拨千斤”的效果,帮助小学生真正解决较为困难的应用题;另一方面,数学本身就是一门与图形、图形密不可分的学科,在应用题中这一特点更是体现得淋漓尽致,很多应用题需要学生去画线段图、平面图、立体图、集合图、统计图,然后据此分析题目、理解数量关系、解决实际问题。为了进一步发挥画图策略在应用题教学中的价值,教师应该从将知识化静为动、将知识化繁为简、实现数形结合、增强学生画图兴趣四个维度出发,让学生掌握画图这种策略,直观、正确地解决问题。
一、利用画图策略,将知识化静为动
小学时期的学生正是汲取数学基础知识的起步阶段,他们善于观察,直观思维占据主要的地位。小学阶段,随着数学学习的深入,越来越多的应用题会以纯文字形式呈现,这些问题在语言表述上言简意赅、逻辑性强,以至于直观思维占据主要地位的小学生经常读不懂题意,进而走进误区,即便最后解决了应用题,也走了很多弯路。因而,在数学实际问题的教学时,教师要基于学生的形象直观思维特点建构数学理解活动的过程,促进学生的数学直观思维向抽象理性思维发展。俗话说:“授人以鱼,不如授之以渔。”教师不能只教学生如何解题,还要交给其解题的方法,这就需要引导学生在草稿纸上进行画图,利用示意图等形式将抽象的问题具象化,在画图中体会方法、学习逻辑,从而还原应用题的本来面目,让学生更容易地解读题目,把握其中的重点和难点。
例如,在教学“比……多(或少)”的数学实际问题时,有的学生往往会形成习惯性思维——“遇到了多就加,遇到了少就减。”但是二者之间也是存在转化关系的。例如,在教授“小灰兔有10只,小灰兔的只数比小白兔的只数少5只,那么小白兔有多少只呢?”首先,教师让学生对题目进行两遍阅读,而后找出已知条件:①小灰兔的只数是10只;②比小白兔少5只,问题:小白兔有多少只。接着,教师指导学生将问题中的已知条件与问题用直观的线段图进行建构(如图1)。
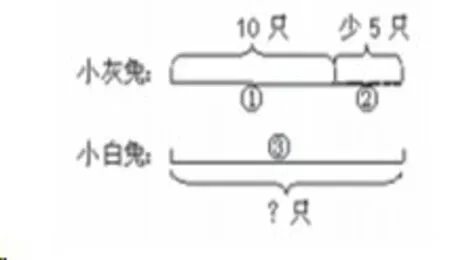
图1
继而让学生说出自己的想法,如何解决这道题。最后,教师进行小结,并板书:小白兔的只数=小灰兔的只数+5只,即10+5。通过线段图直观观察,学生能轻松地从习惯性思维中转变过来,清晰地理解题意,轻松地理清条件与问题之间的等量关系,实现数学应用题的高效性解决。同时,要指导学生经常进行作图练习,小学生利用画图不足的原因往往是找不到画图的思路、想不到画图,这就需要教师在应用题教学中加强画图意识的渗透,让学生先从简单的层次入手,如对会做的应用题进行画图,利用画图来检验自己的解题过程和结果,再逐步提升,对画图的方法和规律进行充分掌握,使其切实利用好“画图”这一“利器”,从而提高学生的思维能力和数学素养。
二、利用画图策略,将知识化繁为简
在小学数学实际问题教学中,“和倍、差倍”应用题往往是考查学生逆向性思维的习题。文字表述中的内容较为繁杂,学生难以弄清题意,由此也带来课堂教学的低效。所以,教师要善于引领学生利用画图的策略,将条件与条件之间的关系化繁为简,促使学生轻松地找出数量之间的等量关系,进而能轻松解决数学的实际问题。
例如,教授“小明与他爸爸的岁数一共是48岁,爸爸的岁数比小明的3倍还多了4岁,今年小明有多少岁呢?”显然,年龄问题中的条件增多了,学生的思考难度增大了。让学生尝试解决,常常发现他们对这一问题无从下手,不知道利用什么运算方法,往往会列出48÷3+4的算式。此时,教师可以引领学生自主绘制出线段图,进行已知条件与问题之间的关系建构。如下图。
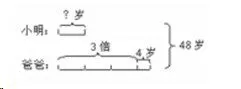
图2
学生就可以直观地看出从爸爸的年龄中减去4岁,这时爸爸的年龄正好是小明年龄的3倍。同时发现了:如果把小明的年龄看作1份,那么爸爸的年龄就是3份还多4岁。通过对线段图的直观观察与数量间的关系建构,学生很快明白了:小明的年龄+小明的年龄×3+4岁=48岁,即小明的年龄+爸爸的年龄=48岁。依据数量间的相等关系,学生自然能列出正确的算式,并有效地完成问题解答。
同时,要对画图解题和一般解题的过程、效率进行对比,让学生切实看到画图的化繁为简的能力。如高年级学生的逻辑能力已经得到了一定程度的发展,也这就要求教师做好有效对比,让他们切实体验画图解题的高效性,激发对学习画图策略的积极性。
三、利用画图策略,实现数形结合
“按图索骥”是利用画图的策略可以让学生直观形象地将素材中的条件与问题建立等量关系,轻松地厘清解题的正确思路,有效地激发学生的学习兴趣,从而促进学生将知识更好地巩固与内化。图形的绘制操作不仅培养了学生的动手操作能力,也促进了学生对解题模型性的初步建构;图形的解释也培养了学生进行数学语言的表达能力,与此同时激起了学生善于动脑的主观能动性,锻炼了数学思维能力,在潜移默化中发展了学生的数学学习综合素养。在利用画图策略解决实际数学问题的过程中,实现数形结合。
(一)学会层次性画图
在数学应用题的解决中,教师要积极指导学生进行画图,提升小学生的画图能力。小学一、二年级的数学知识学习皆为数形结合式的例题与习题教学,多为直观式解决数学问题。然而到了高年级阶段,用文字语言叙述的数学问题逐渐增多,由低年级的直观理解逐渐转变为高年级的抽象性理解。为了将直观思维更好地向抽象思维的发展,教师就要让学生学会自主地将数学文字语言与图形语言建立对应关系,学会从图形的直观层面理解抽象的数学实际问题。在具体画图学习中,教师授以学生各种画图的方法,要依据不同的题型进行。
例如,在学习“……比……多(或少)”的线段图时,首先要确定用一条线段表示标准量,而后再画出增加或减少的部分,以此表示比较量,最后再表示两种数量间的关系。例如,在解决行程类应用题时,首先要用一条线段表示两地的距离,而后分别表示两种交通工具在两地行驶的速度、时间等,将路程、速度与时间这三个量建构好直观关系。要让学生画好线段图,教师就要积极采用以下的路径进行:一是要让学生会说如何画,思考画图;二是要让学生跟着教师画,模仿画图;三是要让学生自主画,尝试画图。
在具体的画图中,教师还应让学生做好以下几个方面:一是读题、审题,找出应用题中数量间的对应关系;二是理清所作线段图的各个部分的长度关系,分清画图顺序;三是有序画图;四是标注好线段图上的关键性条件与问题;五是学会检查,看线段图与原题之间的吻合关系,依据题意,合理修改,完善好线段图。
(二)学会用画图解决问题
学习画图最终的目的是解决问题。在学生完成数学线段图的制作后,教师要让学生说出关键的已知条件与问题,将各个条件与问题之间建构好数量间的等量关系,从而利用数量间的等量关系进行列式,解答应用题。例如,在教授“甲、乙两个工程队合开一条720米长的隧道,同时各从一端开凿,经过24天开通。甲队每天开凿14.5米,乙队每天开凿多少米?”这道题时,首先,教师给予学生画线段的时间,让学生用线段图表示本题中的已知条件与所求问题;接着,让学生厘清“甲队共开凿的米数”“乙队共开凿的米数”与“720米”之间的运算关系;最后,让学生利用好线段图,提取主要关键词,明白算理:“合开的隧道长度一甲队开凿的米数,即得出乙队开凿的米数;然后用乙队开凿的米数除以开凿的天数,即得到乙队每天开凿的米数。”利用好线段图的直观性,学生就能轻松挖掘数量间的一层又一层关系,从而能清晰发现问题解决的路径,实现问题的正确解答。
(三)学会以画图认知概念
学生初步看到应用题目后,在进行画图一定会是以自己的思维为主导,再进一步绘制图形后解决问题,这也是学生逐步形成适合自身的数学概念的重要路径。借助这种“文字获取-图形转化-问题解答”的闭环反馈过程,学生能够不断提升自身的数学建模思想,进而形成空间概念能力。这其中的图形转化是闭环枢纽,也是最为有效的教学手段。教师要善于利用多种多样的教学方式和媒介,最大限度地帮助学生构建数学概念框架,答疑解惑,尽快完成“授人以鱼”到“授人以渔”的转变。例如,学习圆锥、圆柱、球的概念时,单以平面图形表述,学生在认知上会有困惑:为什么画球体就是用圆和椭圆画?为什么圆柱和圆锥画起来像长方形和三角形?即便教师提前引入三视图的概念,学生的理解还是会有偏差,造成“失真”。因此,教师需要用三维呈现这几种图形,充分发挥多媒体教学工具的作用,在三维角度将图形特点展现给学生,帮助学生构建三维空间的概念框架。
四、利用画图策略,激发学生兴趣
兴趣是最好的老师。要想让学生熟练掌握画图这种策略,不断提升解题能力,实现数学思维的不断发展,就要利用各种方式增进学生对画图策略解题的兴趣。教师在课堂上进行教学时,要紧扣教学实际要服务教学目标这一原则,根据学生的年龄特点,心理发展个性,将单纯枯燥重复的画图策略变换成符合学生“口味”的教学方式,让学生在轻松愉悦的环境中开展画图策略解题的过程,调动学生的积极性,从“我要学着画”到“原来这样画”,再到“我要主动画”,最终达到事半功倍的培养效果。
首先,要引导学生感受画图策略的多样性,画图形式多种多样,除了前文所述的线段图、平面图、立体图,学生还可以根据自己的理解画实物图、示意图,教师应该鼓励学生多尝试各种画图形式,大胆提出自己的不同见解,从而真实感受到画图解题的价值和趣味。例如,在进行数学分数解决问题的教学中,由于各种数量关系复杂多元,且每道题都对应着更深刻的理解,因此学生的解题和学习过程都较为枯燥,而此时如果能引导学生采用多样性的画图策略,就能达到事半功倍、一目了然的效果,并增强学生的兴趣。教师可以设计一组扇形图作为表达对象的思维训练,即让学生把自己的理解利用扇形图“解释”出来,例如,100x1/4就是将一个面积为100的圆形平均分成4份,其中点一份就是100x1/4。也可以设计一组趣味图,例如,5x1/5就可以设计成5个西瓜,从中取一个西瓜。在画的基础上,让学生去看应用题与画图表达的意思是否一致,教师再对相关算式进行讲解。随后,教师可以要求学生进行一定的“润色”,遇到一些较难的应用题及相关算式,可以在画图上多增加一些文字信息,图文结合,使表达更具有逻辑性和清晰度。最后,还可以让学生进行“看图编题”,即利用现在所作的图,学生出一道应用题给自己,如“学校有20个篮球,10个足球,篮球比足球多出几分之几”,让学生从画图回归数学思维,再经历一次由具体到抽象的解释过程,从而实现数学思维的训练、知识内化程度的提升。
其次,要发掘画图的无限魅力,画图的价值在于一目了然,可以直观呈现数量关系,帮助学生快速掌握解题重点,因此,教师要重视对“图”意识的正确渗透,引导学生多画一些草图,通过草图正确表达自己的想法。很多应用题来自生活,学生在画草图的过程中可以瞬间找到熟悉的感觉,把文字信息还原成生活中的实际问题,让学生在这种“由里及表”的表达训练中发掘画图的无限魅力,养成画图解题的思维方式。例如,针对这一题目“成本2.5元的中性笔1200只,按照期望获得40%的利润定价出售,当卖出80%后,剩下的中性笔打折扣,最终获得预定利润的86%,请问剩下的中性笔打了多少折扣?”在这一应用题难度很高,教师可以引导学生去画草图,而教师在讲解时也应利用思路分析的草图,把题中原本的信息用画草图的方式进行表达,更快速地解决此题。而在此过程中,可以让学生模仿教师的画图,从而直观地看到复杂的问题被简单化。
总之,数学这门学科本身具备数结合的特征,“画图策略”应贯穿于整个小学数学解决问题的教学中。在小学数学应用题教学中,教师要依据学生的直观性思维向抽象思维能力发展的特点进行教学环节的设计与实施,引领学生学会运用数形结合思想方法,在应用题的解决中利用好画图策略,解决数学实际问题,在数学应用题的解决中,让学生学会分析问题、有序思考、善于归纳,不断提升数学综合学习能力。

