基于联合优化技术的单臂行星架轻量化设计
张成标,阙洪军,杨海师,张理伟
(重庆齿轮箱有限责任公司,重庆 402200)
0 引 言
行星架作为行星齿轮传动中主要构件之一,承受其较大的外力矩,有较大的尺寸与质量,结构也比较复杂,且行星架的结构设计对各行星轮之间的载荷分配和传动机构的承载能力、噪声和振动等都有很重要的影响[1]。常见的行星架结构有双臂整体式、双臂装配式和单臂式[2]。单臂行星架结构的齿轮箱对质量的要求相对苛刻,在传统设计中,行星架多是凭经验公式或材料力学经简化模型而得出的公式进行设计,盲目性大,设计参数较为保守,造成行星架的尺寸、质量一般比较大[3]。因此,通过结构优化,在保证行星架结构刚度前提下,降低行星架质量有着十分重要的意义。
随着拓扑优化理论的不断发展与完善,拓扑优化技术被广泛应用到工程中[3]。宁晓斌等[4]采用拓扑优化方法,对液压挖掘机斗杆结构进行拓扑优化仿真,在保证强度的前提下降低了斗杆的质量。董惠敏等[5]以双壁整体式行星架为研究对象,建立拓扑优化数学模型,应用有限元件对其进行拓扑优化,根据材料分布建立行星架的概念模型,并进行结构设计。
拓扑优化的目的是在给定的设计域内寻找最优的材料分布,但拓扑优化后会使其结构刚度小幅降低,因此需要通过擅长参数、尺寸优化方面的尺寸优化来弥补。张瑞等[6]采用拓扑优化与尺寸优化相结合的方法,进行隔爆型接线盖加强筋优化设计,确定最优加强筋筋型。李修峰等[7]以气瓶支架结构减重为目标,运用拓扑优化获得支架的基本构型,然后对支架主要特征参数进行尺寸优化,确定较为合理的截面尺寸,最后验证设计的合理性。
笔者以单臂行星架为对象,基于有限元软件通过联合优化技术的方法,先将行星架臂板结构进行拓扑优化,后调整行星架臂板厚度尺寸,对其尺寸优化调节,对比各组行星架模型后,选择最佳模型,在满足行星架刚度不变的前提下,实现单臂行星架结构的轻量化。
1 联合优化的数学模型
1.1 结构拓扑优化的数学模型
结构拓扑优化是指在限定的给定边界条件的设计空间中,通过一定的优化方法,找到满足设计约束和设计目标的最佳结构。拓扑优化的方法很多,文中采用工程上常用的基于相对密度分布的拓扑优化方法进行行星架的优化设计,优化目标为最小柔度[9-10]。
相对密度法是一种常用的拓扑优化方法,其原理是假想设计区域的密度在0~1之间是可变的,与初始材料密度存在非线性关系;同样道理,弹性模量也是如此。
构建材料的密度和弹性模量的数学模型:
ρ(x)=xeρ0
(1)
(2)
式中:ρ0为材料的初始密度;E0为材料的初始弹性模量;xe为单元的相对密度;p为刚度惩罚因子。
则以最小柔度为目标函数的拓扑优化数学模型为:
(3)
(4)
KU=F
(5)
0≤xmin≤xe≤1
(6)
式中:U为总体位移矩阵;K为总体刚度矩阵;Ue为单元位移矩阵;Ke为单元刚度矩阵;N为单元数量;f为体积分数。
1.2 尺寸优化的数学模型
尺寸优化的实质就是求解满足约束条件下的自变量构造函数的最小值问题,约束变量也称为状态变量,为自变量的函数,尺寸优化数学模型一般形式为:
目标函数:
min:f(X),X=[x1,x2,…xn]T∈Rn
(7)
状态变量:
gu(X)≤0,u=1,2,…,m
(8)
hv(X)≤0,v=1,2,…,n
(9)
2 行星架联合优化
文中基于有限元软件对行星架结构联合优化,图1为行星架联合优化流程图,首先对初始几何模型进行拓扑优化,根据保留的体积分数不同,需要进行多次拓扑优化,然后根据各组拓扑优化结果建议对应的几何模型,对几何模型进行结构分析,并将行星轮轴的挠度与初始模型对比,研究拓扑优化后挠度变化规律;然后对行星架臂板厚度进行尺寸优化,使其行星轮轴挠度降低到拓扑优化前的水平,得到的6组行星架几何模型,在这6组几何模型中筛选出最合理的模型作为最终模型。

图1 行星架联合优化流程图
2.1 行星架臂板的拓扑优化
2.1.1 优化区域的选取
由于行星轮轴与行星架采用过盈配合,且之前存在轴向定位面,所以行星架的行星轮安装孔周围需要留出非优化区域,以保证行星轮轴与行星架连接的可靠性。行星架臂板的优化区域如图2所示。
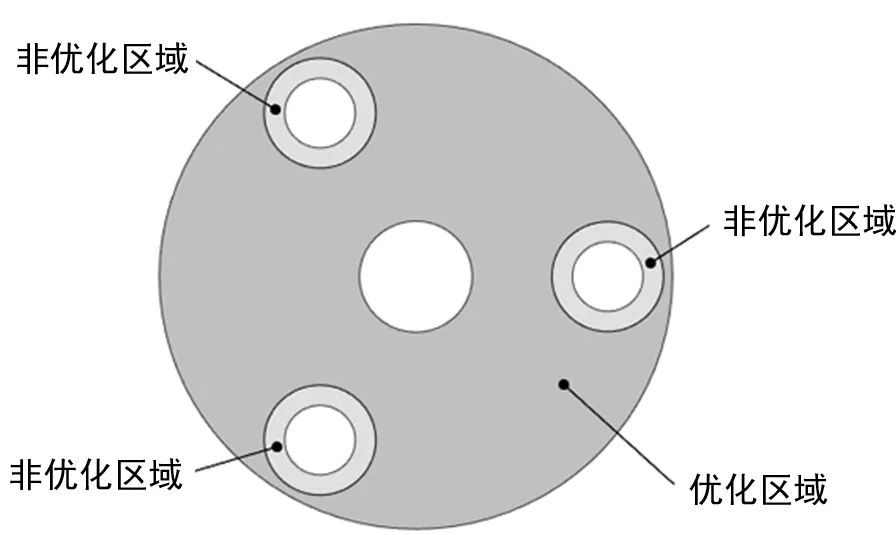
图2 行星架臂板优化区域
2.1.2 优化变量的设置
优化区域保留材料的体积分数从30%~80%分6个程度,为保证三个行星轮轴位置一样的优化结果,添加循环对称的约束条件;为保证行星架臂厚度方向优化结果的一致性,故采用壳单元进行拓扑优化分析;如图3所示。

图3 行星架边界条件施加
采用节点耦合的方式对行星架加载,加载位置为行星轮轴承中心,约束行星架输出内孔的全部自由度。为了解决拓扑优化结果存在多孔材料分布问题,将刚度惩罚因子设置为p=3[11]。
2.1.3 优化后的模型
图4为不同优化程度下的材料密度分布云图,可以看出,随着保留材料的体积分数降低,行星轮孔间区域材料密度接近于零的越来越多。通常,材料相对密度大于0.6的区域要被保留,小于0.4的区域要被舍弃,0.4~0.6为过渡区域。

图4 不同优化程度的材料密度分布
2.1.4 优化后模型分析
根据2.1.3节的拓扑优化结果,去除材料相对密度小于0.6的区域,并光顺边缘区域,构建各个优化程度下的几何模型,并将行星轮轴装配到行星架上,如图5所示;未优化前的几何模型如图6所示,为了便于对比,将其体积分数定为f=1。
对各行星架有限元模型施加相同的边界条件进行分析,行星架与行星轮轴配合为0.036 mm,各行星轮轴上轴承安装位置施加轴承载荷15 158 N,约束行星架输出内孔的全部自由度,求解完成后,提取行星轮轴轴线的挠度。
图7为不同体积分数拓扑优化后的行星轮轴挠度曲线,可以看出,与优化前结果(f=1)对比,拓扑优化后行星轮轴挠度是增加的,并且随着拓扑优化保留材料的体积分数的降低,行星轮轴的挠度是逐渐变大,且最大挠度的变化梯度也是逐渐增大的,如图8所示。

图5 拓扑优化后行星架组件

图6 原行星架组件f=1
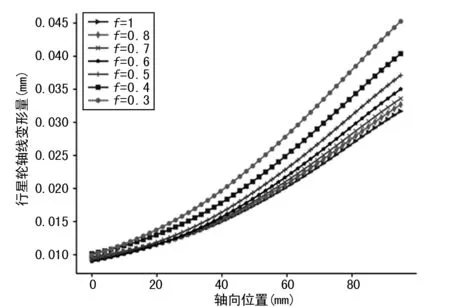
图7 不同体积分数拓扑优化后行星轮轴挠度曲线对比
2.2 尺寸优化
通过前文知道,拓扑优化后,行星架的刚度有所降低,故本节通过对行星架臂板厚度尺寸优化,使各个优化程度下的挠度值达到拓扑优化前的水平。
2.2.1 优化变量设置
以拓扑优化后的行星架组件的体积为目标函数;以行星架臂板的厚度为设计变量,由于拓扑优化后行星轮轴挠度增大,所以臂板厚度采用向上搜索的方法进行;以行星轮轴挠度值不超过拓扑优化前行星轮轴挠度值为状态变量;采用目标函数最小化方法进行尺寸优化。

图8 不同体积分数拓扑优化后的行星轮轴最大挠度
2.2.2 尺寸优化结果汇总
各组行星架均得到满足条件的最合理的厚度值,各行星架臂板尺寸优化后厚度值如表1所列,表中f为模型拓扑优化时的体积分数,f=1表示为未经任何优化的初始模型;H为尺寸优化后的臂板厚度。

表1 尺寸优化后的行星架臂板厚度
图9为各体积分数的模型要达到初始模型的挠度值时,臂板需增加的厚度值,可看出,拓扑优化保留材料体积分数越低,想要达到初始模型的刚度,行星架臂板需要增加的厚度越大;还可看出,随着拓扑优化保留材料体积分数的越低,曲线的斜率绝对值越来越大,这表明,拓扑优化保留材料体积分数的越低,通过增加臂板厚度补偿刚度损失变得越来越难。

图9 不同体积分数的行星架臂板厚度增加量
2.3 最终模型
在2.1节中利用拓扑优化可以降低行星架的质量,在2.2节中为了让行星架达到初始模型的刚度进行了尺寸优化,增加的行星架的质量。图10给出了6组行星架模型经过联合优化后的质量变化曲线,通过曲线可以看出,拓扑优化体积分数取0.5时,再配合尺寸优化,使行星架刚度达到初始模型,可以使行星架的最终模型质量降到最低。联合优化后的最佳模型如图11所示。
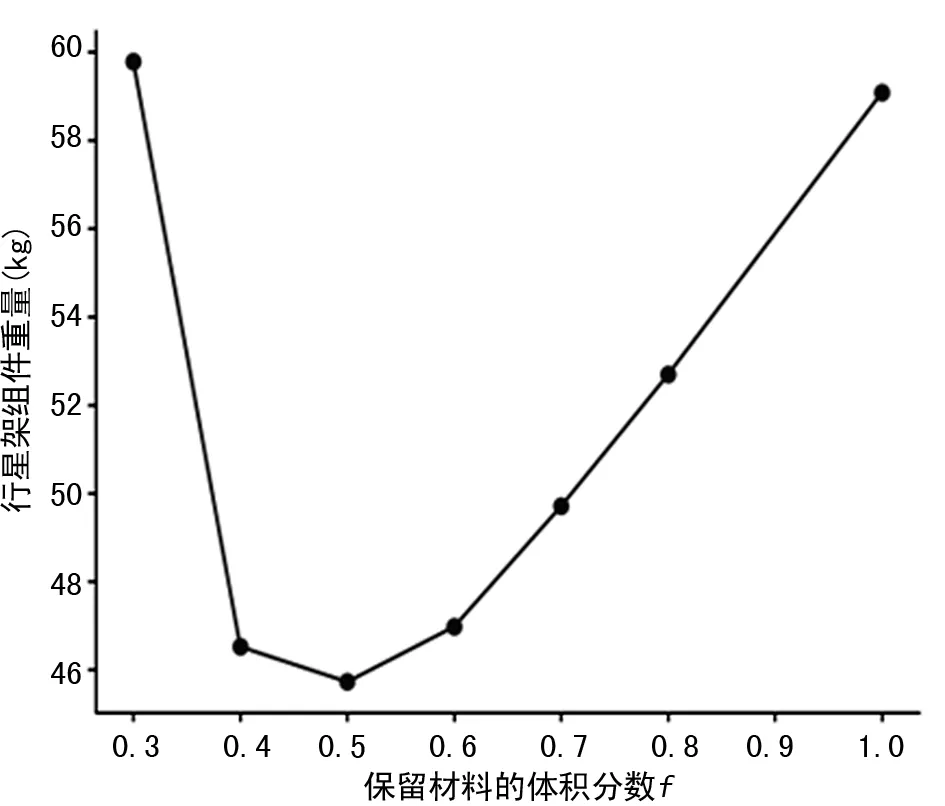
图10 各组行星架组件联合优化后的质量

图11 联合优化后的行星架组件最佳模型
3 结 语
文中通过拓扑优化和尺寸优化相结合的方法进行了行星架的轻量化设计,确定了最合理的优化路线,即:先进行保留体积分数为0.5时的行星架臂板拓扑优化,获得最佳的材料分布,拓扑优化后建立行星架组件的几何模型,以最小化行星架组件体积为目标,以行星轮轴刚度为状态变量,以行星架臂板厚度为设计变量,最后得到行星架臂板厚度为61.6 mm。此时行星架组件质量为45.727 kg,初始行星架组件质量为59.085 kg,通过联合优化,在满足行星架刚度不变的前提下,行星架组件的质量降低了22.6%,取得了显著的减重效果。

