基于通用翼型的小型风力机叶片结构设计与性能分析

兰 平，王旭东

(重庆工商大学制造装备机构设计与控制重庆市重点实验室，重庆 400067)

0 引 言

叶片是风力机的关键部件之一，是进行能量转换的重要组成部分，其优越的气动性能设计和合理的加工工艺制定是风力机可靠高效工作的关键。

小型风力机叶片的设计一般都是采用单一翼型，着重考虑其气动性能，以最大风能利用率为目标采用传统的风轮空气动力学理论来完成其设计过程[1]。而小型风力机叶片制作方法现在主要都是基于纤维复合材料来完成，制造工艺主要有手糊成型、模压成型、预浸料成型、挤压成型、纤维缠绕、树脂传递模塑以及真空灌注成型等工艺[2]。笔者通过建立修正的风力机风轮空气动力学模型，在完成叶片气动外形设计的基础之上，基于叶片的三维实体模型，对叶片进行了结构强度有限元分析，进而对叶片的制作工艺及加工组装完成的风轮性能测试进行了研究分析，系统的提出了小型风力机叶片的设计制造及测试过程。

1 通用集成翼型的性能分析

风力机叶片形状主要由翼型形状、弦长、扭角以及翼型相对厚度分布来确定。风力机通用集成翼型的设计理论是从表征翼型型线本质特征的根本因素，即翼型的形函数出发，通过应用一种比较高效的形状函数来表达的方法，来达到更精确的控制翼型的集成精度和叶片的形状的目的。这样不仅能够让设计出的风力机叶片具有很高的捕风效率，并且能够在不同的环境下也能保持相应的高效率和综合应用各个学科领域优势等一系列的高性能，同时能够保证叶片表面形状的光滑性以及叶片形状的最大程度最优解。文中在进行叶片气动外形设计时，叶片翼型采用自主设计性能优越的最大相对厚度为18%的风力机通用集成翼型[3]，其形状如图1所示，翼型的相对厚度沿展向不变。在雷诺数Re=1.6×106时，为了尽快分析所设计的叶片的气动性能进行分析，这里使用Xfoil程序，图2表达的是当翼型的攻角在逐渐增大过程中升力系数的变化情况，从图中看出升力系数增大到1.87后就不再增大，对应的攻角数值为19°，表明设计结果失速比较迟缓。根据图3中展示的同一工况下攻角对升阻比变化情况的影响可以看出在攻角取值5°时，升阻比达到了同等条件下的最优值：150.09。

图1 叶片翼型的形状 图2 设计翼型的升力系数 随攻角变化图

图3 设计翼型在主要工作攻角区域的升阻比

2 叶片的气动外形设计

风力机叶片在进行形状设计时，首先确定风轮的基本参数。一般来说，小型风力发电机在设计风速8～10 m/s下，具有最大风能利用系数。选取风轮的额定风速为9 m/s，叶尖速比为7，额定功率为2 kW。

应用一维动量理论建立风力机风轮空气动力学模型时，可以把风轮视作有无数的叶片拼成的一个大圆盘，因此，在进行风轮气动特性计算时，Prandtl提出了叶尖损失修正因子：

(1)

式中：F为普朗特叶尖损失修正因子；B为叶片个数；R为风轮半径；r为叶片径向位置；φ为入流角。

以动量-叶素理论为基础，对风轮叶素理论中翼型的法向力和切向力系数(Cn,Ct)做了进一步的修正[4]：

(2)

g=exp[-0.125(Bλ-21)]+0.1；

得到了风轮的轴向和周向诱导修正因子分别为：

(3)

(4)

其中：Y1=4Fsin2φ/(σCnF1)

Y2=4Fsinφcosφ/(σCtF1)

通过迭代求解，可以计算在不同风速和转速下风轮承受的载荷及其输出功率等特性，进而完成叶片各个截面的形状参数确定。在迭代过程中，以0作为轴向诱导因子a和周向诱导因子b的初值，根据此初值，逐步计算入流角、攻角、翼型的法向力和切向力系数，最后再得到新的轴向诱导因子a和周向诱导因子b的计算值。比较最新计算的a和b值与上一次的a和b，如果两者的误差小于我们设定的误差值，则认为迭代求解过程完成，否则继续迭代。为了保证计算精度，根据相关文献，文中的迭代误差初值选取为0.001。

设计完成的风轮在额定风速9 m/s时，额定输出功率为2 kW，叶片的长度为1.8 m。图4为设计叶片的弦长分布，最大弦长为0.23 m，在叶片展向距根部0.29 m处。图5为设计叶片的扭角分布，最大扭角为12.4度，整个扭角变化沿叶片展向较为平缓。

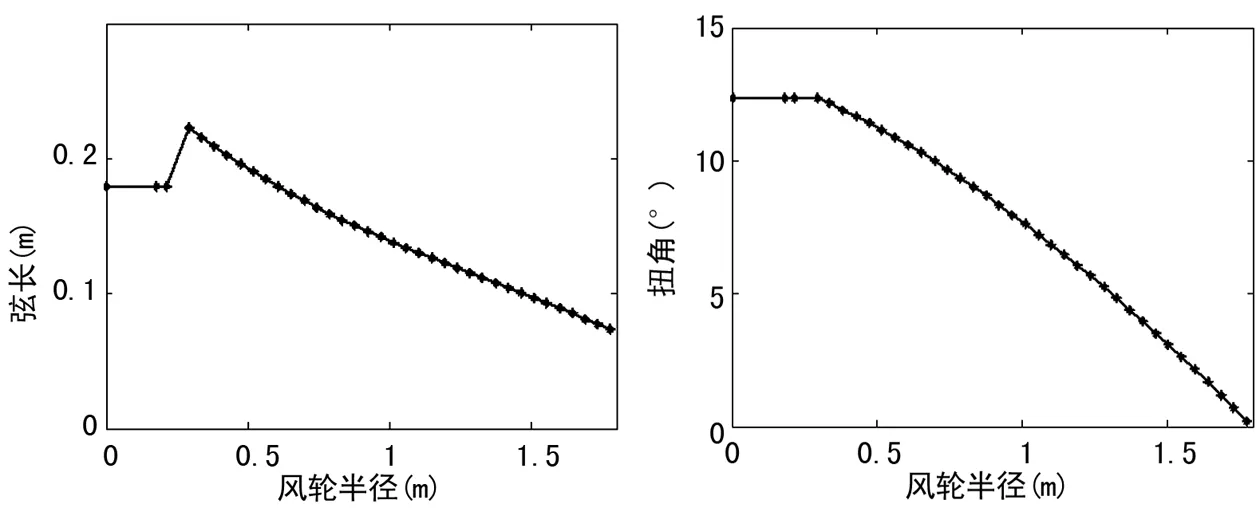
图4 叶片的弦长分布 图5 叶片的扭角分布

3 设计叶片的结构强度分析

叶片是整个风力发电机最为重要的部件，它将在空气的推动力下做旋转运动，进而实现风能与机械能之间转化。叶片所受的力主要来至于与之接触的空气，而空气属于流体，这就致使叶片的受力情况比较复杂。整个风力机机组的工作年限很大程度上是与其叶片的极限工作时间有关，因而，所设计的叶片需要满足在运行环境下的所需要的结构条件。基于上节得到的叶片设计参数，在SolidWorks软件中建立叶片的三维模型如图6所示。

将在SolidWorks里建立的生成的叶片的三维模型图输出为x_t格式，把保存下的模型图导入到ANSYSWorkbench中进行有限元分析。叶片的材料选用玻璃钢，单元类型选择为壳单元，完成叶片的有限元网格划分。划分好网格后，确定其边界约束条件，叶片的实际工作情况是所有的叶片都是是用螺钉与法兰盘在根部进行连接在一起的，因而在对叶片的结构进行分析时吧叶片的连接部分作固定端处理就行。叶片的有限元网格如图7所示。

图6 叶片的三维实体模型 图7 叶片的有限元网格模型

选取极端风速为20 m/s，考虑该极端风况下的受力情况，缝隙叶片所能承受的极限应力(重力、离心力、轴向推力等产生的拉压应力以及扭矩产生的切应力)。将叶片在风速20 m/s下受到的极端载荷以面里的方式施加在叶片的迎风面上，在ANSYSWorkbench中可以通过施加压力Pressure的方式进行施加，求解可以得到叶片的应力应变分布。图8为叶片的应力分布云图，根据应力的变化情况可以得出来相对于叶片材料的极限应力来说叶片的整体受到的力十分微小，最大的应力值在15.051 MPa，发生在叶片根部与轮毂连接处，最大应力远小于叶片材料玻璃钢的屈服强度。

4 风轮输出功率的测试分析

叶片作为风力机风轮的主要构成部分，工作时要不仅要受强烈阳光的爆晒、大雨的腐蚀等极端天气的环境的破坏，同时要承受风轮旋转引起的气弹结构载荷。因此，叶片材料一般选用纤维增强复合材料，此类叶片在强度及其密度方面占据很大的优势，且具有较好的抗疲劳、抗冲击、抗蠕变特性[6]。文中叶片模型的材料选用玻璃纤维复合材料。加工相同的3个叶片，进行组装成风力机风轮，如图9所示，3个叶片应对称分布，互相间隔120°角。搭建风力机输出功率的测试实验平台，其原理为首先通过风速测试仪测试和控制自然风来流的风速，保证具有稳定的输入风速。其次，将风轮产生的电能通过与三相整流桥连接，稳定其输出电压和电流，并采用相应的电压表和电流表进行数据的读取。测试所得的不同风速下电流乘以电压就是风轮的输出功率，风轮输出功率测试原理如图10所示[7-8]。

图8 叶片的应力分布云图 图9 组装的风力机风轮

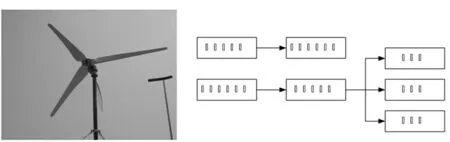
图10 风力机输出功率测试原理

图11～14分别为在平均风速7 m/s，8 m/s，9 m/s和10 m/s下所测得的设计风轮输出功率随时间的变化图。可以看出，功率随时间变化波动相对较大，这主要是由于风速的不稳定引起的。因此，为了确保测试数据尽可能的准确，在研究设计风轮不同风速下的输出功率特性时，在每个风速下，都进行了多个时间段的数据采集，取其多个测点的平均值。其中在额定风速9 m/s下，测得的风轮平均输出功率为1.87 kW，略低于其额定输出功率，这主要是由加工精度以及测试过程中的误差引起的。

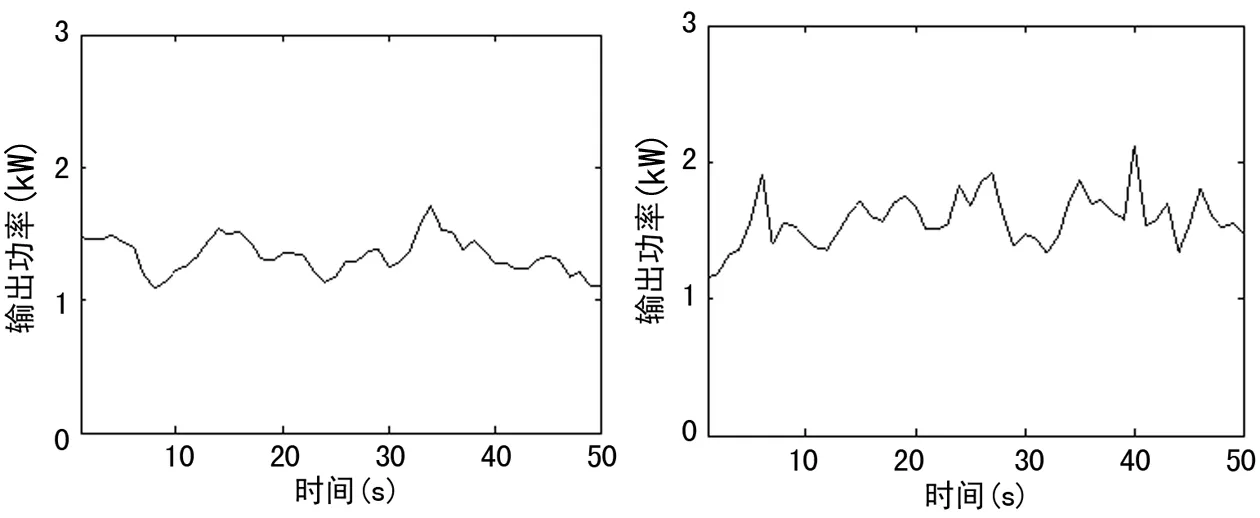
图11 风速7 m/s下风轮的输出功率 图12 风速8 m/s下风轮的输出功率

图13 风速9 m/s下风轮的输出功率 图14 风速10 m/s下风轮的输出功率

5 结 论

(1) 选择相对厚度为18%的风力机通用翼型，基于该翼型完成设计了功率为2 kW小型风力机叶片，应用SolidWorks软件建立了叶片的三维CAD实体模型。在ANSYS Workbench软件中建立了叶片的有限元模型，分析其极端工况下的结构强度。

(2) 采用玻璃纤维材料，完成了叶片的加工制作并进行了风力机风轮的组装，给出了风轮输出功率的测试原理，在搭建测试平台上测试了不同风速下风轮的输出功率情况。对比发现，测得的额定风速下的输出功率值略低于理论值。文中叶片的静力结构分析以及不同风速下风轮的输出功的测试结果，给风力机叶片的设计制造提供一定的理论基础。