某电动物流运输车车架强度分析及结构优化

张明杨，任爱华，孙章栋，张 楠

(湖北汽车工业学院，湖北 十堰 442000)

0 引 言

车辆行驶过程中，来自内外的各种载荷作用于车架上[1]，其力学性能对整车的承载能力和安全性有重要影响[2]，因此利用有限元法对车架进行静力学分析，提高其可靠性具有重要意义[3]。葛彦竹和张铁山根据对车架进行静强度分析的结果改进其结构设计，提高了车架的可靠性[4-5]；吴凯佳基于对车架的静力学分析进行优化，减轻车架重量同时提高模态频率[6]；陈远帆和王亮以强度分析结果为基础，对车架优化提高了车架可靠性同时达到轻量化的目的[7-8]；周友明通过对车架进行强度分析验证替换材料后的可靠性[9]。

上述文献均以对车架强度的分析为可靠性验证和优化的依据，但设计的工况不尽相同。笔者以HyperWorks有限元软件为分析平台，基于垂直、左转向和右转向三种工况对目标车架进行静力学分析，通过了解各工况下的应力分布从而对车架薄弱处进行优化，使其强度满足性能要求。

1 有限元模型建立

目标车架由十根长梁与若干短梁接合而成，属于综合式车架，车架梁属于矩形管结构，梁与梁之间采用焊接进行连接。车架总长3 880 mm，总宽2 280 mm。

1.1 网格划分

通过去除部分较小的孔、槽结构简化车架模型[10-11]，并根据企业提供网格质量标准(如表1)对车架进行网格划分。标准焊点连接情况用壳单元处理。

表1 网格质量

最终网格划分如图1所示，其中网格单元数量为196 362，节点数量为193 522。

图1 车架网格化

1.2 定义材料属性

材料选用45钢，其各项属性如表2所列。

表2 材料属性

2 典型工况分析

2.1 预设工况

结合车架可能面临的实际工作情况设计三种工况环境，如表3所列。

表3 工况描述

假设使用目标车架的车辆在一般城市道路上平稳行驶，可能产生的加速度和选用的安全系数见表4所列。

表4 给定系数

2.2 创建约束

结合实际情况，在车架悬挂和板簧处创建约束，以图3中有限元软件的全局坐标为参照，建立一个用以描述约束情况的坐标系，xyz轴正方向与软件所示全局坐标一致。

车架在垂直、左转向和右转向三种工况下的约束情况见表5所列。

表5 约束情况

添加约束位置如图2中箭头指示位置所示。

图2 约束位置描述

2.3 分布载荷

如图3所示，车架所受载荷主要来自于水箱、电池包及其他电器。

按照设计要求，设水箱质量1 000 kg，电池包及其他电器质量400 kg，通过刚性单元Rigids将其产生的载荷均布加载在车架与其接触部分的网格节点上，如图4。

图3 车架载荷结构 图4 车架载荷

三种工况下车架载荷如表6所列。

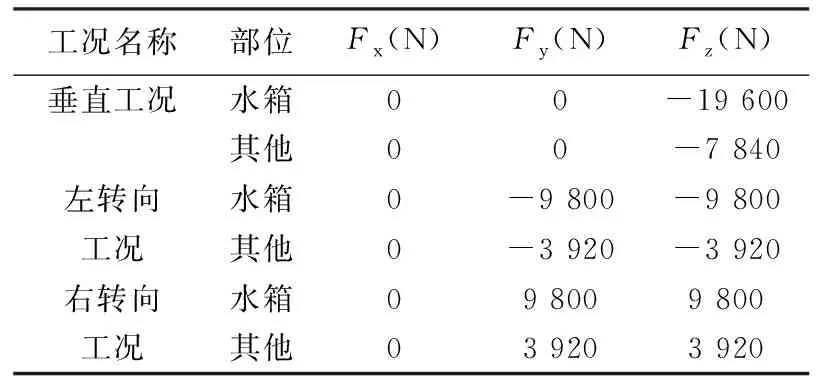
表6 不同工况下车架载荷

3 计算结果与分析

进行静力学分析，得到目标车架在垂直、左转向、右转向三种工况下应力云图，如图5所示，其中箭头标注处为最大应力处。

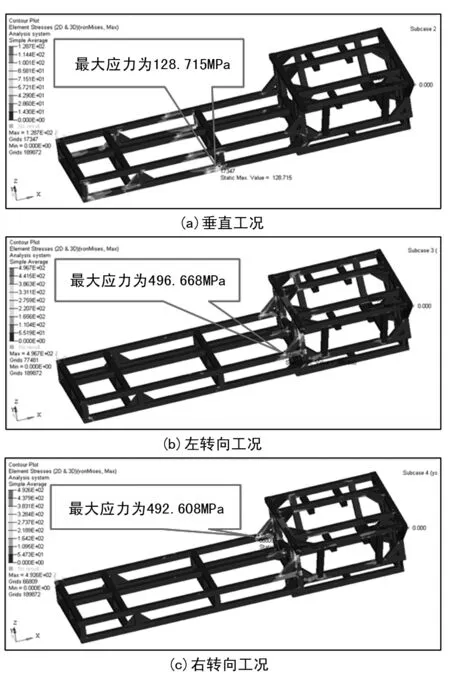
图5 车架应力云图

三种工况下最大应力情况如表7所列。

表7 最大应力情况 /MPa

结果表明，垂直工况下最大应力小于45钢屈服强度，左转向工况和右转向工况下最大应力均大于45钢屈服强度。

4 优化设计

为满足车架工作时的强度需求，使车架最大应力小于材料屈服强度，通过增加x,z方向的支撑梁分担载荷(如图6所示)，从而达到使薄弱处最大应力变小的目的。

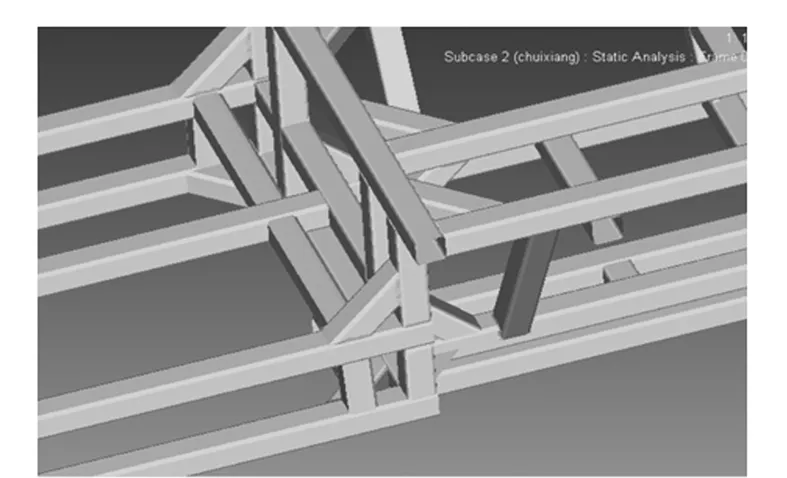
图6 加强筋示意图

加装支撑梁后，左转向、右转向工况应力最大处位置不变，如图7、图8所示。

优化后薄弱处应力大小见表8，最大应力分别减小了38.32%和37.88%，均小于材料屈服强度，满足性能要求。

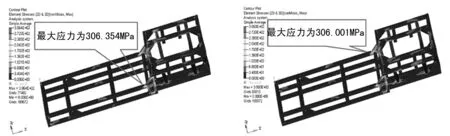
图7 优化后左转向应力云图 图8 优化后右转向应力云图

表8 最大变化应力情况

5 结 语

以某物流车车架为研究对象，通过有限元软件进行静力学分析，发现仅垂直工况下车架强度满足性能要求；在左转向和右转向工况下的最大应力分别为496.668 MPa和492.608 MPa，超过了材料屈服强度。采用添加支撑梁的方法对车架进行结构优化，优化后车架在左转向和右转向工况下的最大应力分别为306.354 MPa和306.001 MPa，分别减少了38.32%和37.88%，满足了车架强度要求，增加了该车架的使用寿命。