一个涉及多重可变上限函数的半离散Hardy-Mulholland型不等式
吴善和, 黄先勇, 杨必成
(1. 龙岩学院数学系, 龙岩 364012; 2. 广东第二师范学院数学系, 广州 510303)

(1)
有趣的是,在类似于式(1)的条件下,有如下具有相同最佳常数因子的Hardy-Mulholland不等式[1]:
(2)
2006年,应用Euler-Maclaurin求和公式,KRNIC和PECARIC[2]建立了式(1)的如下推广式:
(3)
其中,λi(0,2](i=1,2),λ1+λ2=λ(0,4],常数因子B(λ1,λ2)是最佳值,其中为Beta函数。当p=q=2,λ1=λ2=λ/2,由式(3)可导出杨必成[3]关于Hilbert不等式推广的一个结果。2019年,应用式(2)及Abel求和公式, ADIYASUREN等[4]给出了核为1/(m+n)λ且级数的项中涉及部分和的Hardy-Hilbert型不等式。众所周知,式(1)和式(2)及其积分形式在分析学及相关领域有重要的应用[5-12]。
2020年,黄启亮等[13]给出一个一般齐次核Hardy-Mulholland型不等式,推广了Hardy-Mulholland不等式,即:

(4)

作为对离散型不等式和积分型不等式的拓展研究,1934年,HARDY等[1]给出了如下半离散Hardy-Hilbert型不等式:

(5)
有关式(5)的一些推广及应用可见文献[14-18]。
2016年,洪勇和温雅敏[19]给出式(1)的推广式中最佳常数因子联系参数的一个等价条件。该结果引起许多学者的兴趣,相关的一些研究成果可见文献[20-26]。2019年,YANG等[27]建立了逆向的半离散Hardy-Hilbert型不等式。2021年,HUANG等[28]利用积分上限函数和级数的部分和给出了一些新的半离散Hardy-Hilbert型不等式。
黄启亮等[13]通过引入多个参数和齐次核函数推广Hardy-Mulholland不等式,建立了形如式(4)的离散型Hardy-Mulholland不等式。本文从研究半离散不等式的视角,通过构造适当的核函数和权函数建立含无穷积分和级数混合形式的Hardy-Mulholland型不等式:首先,通过引入核函数1/(lnnex)λ和权函数来建立一个涉及参数和多重可变上限函数的半离散Hardy-Mulholland型不等式;然后,探讨该不等式的常数因子为最佳值时各参数之间的相关性及等价陈述,建立其等价不等式,刻画一类具有最佳常数因子的Hardy-Mulholland型不等式的结构特征。
1 若干引理


引理1设s(0,∞),s2(0,1]∩(0,s),ks(s2)∶=B(s2,s-s2)。定义如下权函数:

(6)
则有如下不等式:
(7)

(8)

再由式(8),有
故式(7)成立。证毕。
引理2在引理1的条件下,对于s1(0,s),若


则有如下推广的半离散Hardy-Mulholland不等式:
(9)
证明作变换v=x/lnn,可得到另一权函数表示式:
ks(s1) (n+{1})。
(10)
利用Hölder不等式[29],有
(11)
下证式(11)取严格不等号。若式(11)取等号,则由文献[29]知:有不全为零的常数A和B,使得
a.e.于+×+{1}。
不妨设A≠0,则对于n+{1},有
xp[1-((s-s2)/p+s1/q)]-1fp(x)=
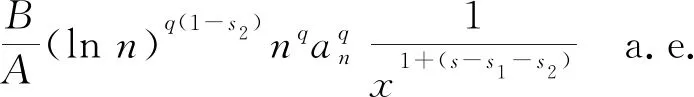
(12)
注1在式(9)中,置换f(x)为Fm(x),并设s=λ+m(m,∞),s1=λ1+m(m,s),s2=λ2(0,1]∩(0,λ),则有s(0,∞),s1(0,s),s2(0,1]∩(0,s)。于是,得到如下含新参数的半离散Hardy-Mulholland不等式:
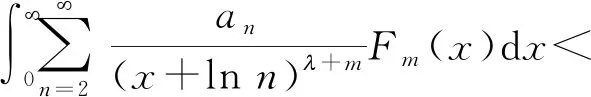
(13)
引理3对于t>0,有如下表示式:

(14)
证明对于m=0,因F0(x)=f(x),式(14)自然成立;对于m+,由分部积分法及条件Fi(0)=0,Fi(x)=o(etx)(t>0;i=1,2,…,m;x→∞),可得
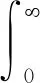
依次代入i=1,2,…,m,即得式(14)。证毕。
2 主要结果
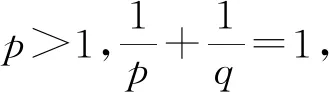
(15)
特别地,若λ1+λ2=λ(λ1(0,λ),λ2(0,1]∩(0,λ)),则有
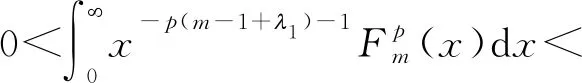
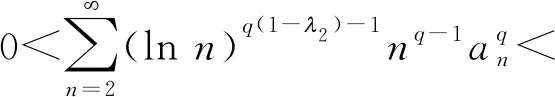
及
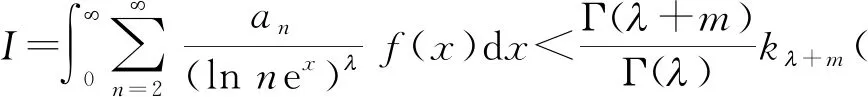
(16)
证明运用换元积分及Gamma函数表示,得
由Lebesgue逐项积分定理[30]及式(11),得到
再由式(13),可得到式(15)。证毕。
定理2若λ1+λ2=λ,则式(15)的常数因子必为最佳值。
证明若λ1+λ2=λ,则式(15)变为式(16)。任给0<ε 对于i{1,2,…,m},设 (17) 从而有 令ε→0+,由Beta函数的连续性,有 (18) 由Hölder不等式,可得 (kλ+m(λ2))1/p(kλ+m(λ1+m))1/q。 (19) Auλ-λ2+m-1=Buλ1+m-1a.e. 于+。 不妨设A≠0, 则有uλ-λ2-λ1=B/Aa.e. 于+,于是λ-λ2-λ1=0,因而有λ1+λ2=λ。证毕。 定理4在满足定理1条件下,有如下与式(15)等价的半离散Hardy-Mulholland不等式: (20) 特别地,当λ1+λ2=λ(0,∞),λ1(0,λ),λ2(0,1]∩(0,λ)时,有如下式(16)的等价式: (21) 证明假定式(20)成立。由Hölder不等式,有 (22) 则由式(20)可得式(15)。若式(15)成立,置 若J=0,则式(20)显然成立。下设0 (23) 即式(20)成立。综上,式(20)等价于式(15)。证毕。 证明若λ1+λ2=λ,则由定理2知,式(16)的常数因子是最佳值,从而得到式(21)(即式(20)取λ1+λ2=λ时)的常数因子是最佳值(注:倘若式(21)的常数因子不是最佳值,则由式(22)可推导出式(16)的常数因子也不是最佳值,从而导出矛盾)。
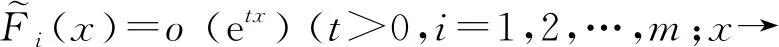


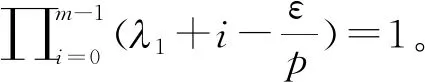
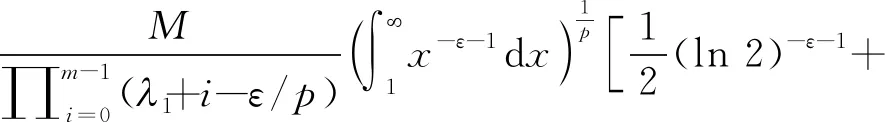


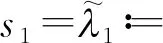

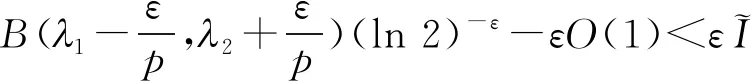







3 等价形式





