典例剖析 有的放矢
文/张 丽

解决方程与不等式类问题,要充分理解方程与不等式的概念,掌握方程与不等式的解法,会用方程或不等式解决实际问题。本文以三个例题为载体,剖析易错点,有的放矢,希望能帮助同学们更好地理解“方程与不等式”的相关内容。
例1已知关于x的方程kx2-2x+1=0有实数根,则k的取值范围是_____。
【错解剖析】部分同学认为这是关于x的一元二次方程,根据方程有实数根,利用根的判别式大于等于0,求k的取值范围。产生错误的原因是对一元二次方程的概念、基本形式认识不到位。只有一元二次方程中含未知数的二次项的系数不为零,才能保证最高次项是二次项,当二次项的系数含参数时,要注意需分类讨论。
【解法思路】此题未指明是关于未知数x的几次方程。观察方程kx2-2x+1=0,发现x2的系数k是否为零,决定了此方程的类型。①当k=0时,方程-2x+1=0为一元一次方程;②当k≠0时,方程kx2-2x+1=0为一元二次方程。
【正解】①当k=0时,方程-2x+1=0为一元一次方程,符合题意;
②当k≠0时,方程kx2-2x+1=0为一元二次方程,
由题意可得(-2)2-4k≥0,
即k≤1且k≠0。
综上所述,k的取值范围是k≤1。
例2若关于x的不等式组无解,则a的取值范围是( )。
A.a≤-3 B.a<-3
C.a>3 D.a≥3
【错解剖析】部分同学易列出不等式3a+2<a-4,漏掉3a+2=a-4这种情况。同学们在复习时应有意识地强化临界值意义的练习,并对不同情况做变式训练。例如:关于x的不等式组无解,求a的取值范围;关于x的不等式组有3个整数解,求a的取值范围等。此类型题均需考虑临界值是否符合题意。
【解法思路】此题考查的是不等式组的含参数问题,解法不唯一。下面列举两种常见方法。方法一:从解不等式组的角度入手,即先求出不等式组的解集,把不等式的解集通过数轴表示出来,根据不等式组无解求出a的范围,此处需重点考虑临界值,即3a+2=a-4是否符合题意;方法二:从函数图像的角度入手,即分别画出函数y1=3a+2,y2=a-4的图像,两线相交于点(-3,-7),观察函数图像可得a的取值范围。这两种方法均借助“形”来求解,即用数轴或函数图像表示出不等式组的解集。数形结合,形象直观。
【正解】由题意可知,3a+2≤a-4,解得a≤-3。故选A。
例3将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友分到苹果但不到8个苹果。问这一箱苹果有多少个?小朋友有多少人?
【错解剖析】设有x个小朋友,列出不等式组产生错误的原因在于审题不仔细,条件“有一个小朋友分到苹果但不到8个苹果”的意思是“有(x-1)个小朋友分到8个苹果,还有一个小朋友分到苹果的数量是大于等于1,小于等于8的正整数”。用不等式(组)解决实际问题,要理清题意,抓住题目中表示不等关系的关键词“至多”“至少”“不超过”“不到”等,找出不等关系,列出不等式(组),最后还要检验解的实际意义。
【解法思路】此题考查的是用一元一次不等式(组)解决实际问题,先设未知数(设小朋友有x人),根据“若每位小朋友分5个苹果,则还剩12个苹果”列出代数式,苹果共有(5x+12)个,再根据“若每位小朋友分8个苹果,则有一个小朋友分到苹果但不到8个苹果”找到两个不等关系,列出不等式组求解,最后要考虑实际意义。
【正解】设有x个小朋友。
根据题意,得
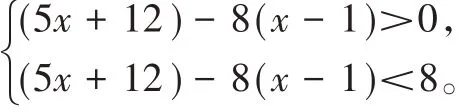
因为x为正整数,所以x=5或x=6。
当x=5时,5x+12=37;
当x=6时,5x+12=42。
答:有5个小朋友,37个苹果或者有6个小朋友,42个苹果。

