整体把握，引导学生思维向更深处漫溯——由教学一道“倍量关系”题想到的

江苏睢宁县双沟镇中心小学（221212）欧慧敏

“倍量关系”问题在小学数学中高年级的练习中经常出现。虽然它的结构不算复杂，思考难度也不是很大，但是面对不同的问题描述时，学生却难以顺利地进行解答，甚至很多学生觉得解决这类问题极其困难，无从下手。因此，要想学生更好地理解“倍量关系”问题，积累相应的数学活动经验，构建解决这类问题的数学模型，教师就要引导学生学习整体把握问题的方法，形成有效的整体感知，从而让思考更有针对性，让问题研究方向更明确，最终解决问题，使学生的数学思维向更深处漫溯。

教学过程

多媒体出示题目：如果把3杯果汁倒入一个玻璃壶中，连壶一起称重是580克；如果把5杯果汁倒入一个玻璃壶中，连壶一起称重是820克。问：这个玻璃壶重多少克？一杯果汁有多少克？

（题目一出示，课堂顿时沸腾起来）

生1：老师，这道题是不是出错了，一会儿果汁，一会儿玻璃壶的，两个问题好解答吗？

生2：这道题中有两个不同的问题，还真是不好解决啊！

……

（教师没有应答，而是采取观望的态度。课堂顿时安静下来，有的学生与同伴交流，有的学生皱眉沉思，有的学生在本子上写写画画……学生都在积极地寻找解决问题的方法）

师：老师发现有部分同学在画图思考，你们的研究有突破吗？

生3：我也试着画图，但是感觉难以画清楚，因为既要画玻璃壶，又要画果汁。

师：是个难题啊！大家一起来开动脑筋，想办法克服这个困难。

（学生再次进行思考和讨论，这次画图的学生明显增多）

生4：我们小组用一个长方形代表玻璃壶，这样就可以往里面倒果汁了。（出示右图）倒入3杯果汁，就在长方形内画出相同的3个小长方形；倒入5杯果汁，就在长方形内画出相同的5个小长方形。不过，只能画出图来，还是没有找到问题的解决方法。

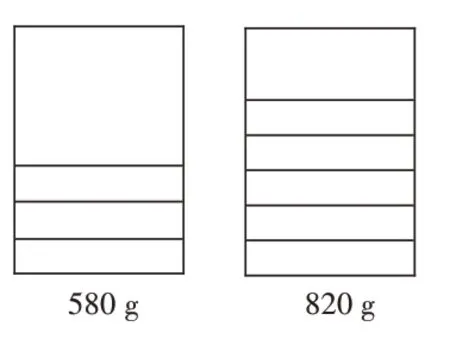
生5：我们小组也是采取画图的方法，不过和你们画的图不一样。（出示右图）我们先把玻璃壶画成一个圆，然后在它的右边画出3个相同的长方形；再同样画一个玻璃壶，在它的右边画出5个相同的长方形。这时我们发现玻璃壶是一样的，它在每一次的称重中都是固定不变的。第一次倒3杯果汁，总重量是580克；第二次倒5杯果汁，总重量是820克。如果把玻璃壶和3杯果汁的部分都去掉，第二次就多出2杯果汁，而重量也就是多出的部分，即820-580=240（克），这240克不就是2杯果汁的重量吗？这样一杯果汁就有240÷2=120（克）。

生6：我有点明白了。就是把前后两次相同的玻璃壶、3杯果汁看成同样多的部分，那第二次多出的2杯果汁就对应着原来的重量差，即820-580=240（克），那么一杯果汁就是240÷2=120（克）。

生7：从图中可知，就是把相同的部分去掉，多出来的2杯果汁就是总重量的差，即240克，那么一杯果汁就是120克。这还真奇妙！通过画图，问题解决起来就容易多了。

师：通过分析图，很容易看出其中的数量关系，所以我们要多学着用画图的策略解决问题。其实，第一位同学的画图也是可以的，只不过理解起来有难度，大家再想想就会有新的思路了。

生8：是的！第一位同学画的图可以先想出来再分析，即580克=玻璃壶+3杯果汁，820克=玻璃壶+5杯果汁，从中就能发现规律了。

生9：你的分析和语言表达非常好。我感觉到用文字来思考也很方便。玻璃壶+3杯果汁=580（克），玻璃壶+5杯果汁=820（克），这样就会发现820-580=240（克），实际上就是2杯果汁的重量，即一杯果汁的重量是120克。

……

师：今天大家研究问题很积极，思考也很有见地。那么，你们有些什么收获？

生10：我感觉画出一个合适的示意图，对研究问题很有帮助。

生11：将画图与文字表达结合起来，也会让问题研究容易些。

师：不错！画图虽然是很好的解决问题的策略，但我们还得把它与数量关系对应起来，这样研究问题的效率会大大提高哦！

……

实践反思

从上述教学案例可以看出，教师给予学生探究的自由与时空，他们可以充分地发挥自己的聪明才智，运用已有的知识经验去分析问题、解决问题，灵动地展示自己的学习个性。同样，这样的学习历程也是学生自我判断、自我反思的过程，对学生学习能力的发展、数学素养的提升大有裨益，也是极具深远意义的。

1.相信学生能行

现代教育学和心理学研究表明：信任是深度交往的前提。同理，教师相信学生能行，则是学生学习的动力之源，更是他们树立美好愿景的力量之源。

基于此，在“倍量关系”问题教学中，教师始终把学生置于探究的最前沿，引导他们尝试、探讨和质疑，使他们不断迸发思维的火花，展现自己的聪明才智。教师则退居“二线”，在必要的时候给予学生指导与帮助，从而保证学生探究的方向不发生偏移，使学生的注意力和兴趣始终聚焦于问题的研究之中。

回顾整个教学过程，出现多次师生对话，从中不难看出，教师真正把问题探究的主动权交给了学生，并给予学生充分的信任。如“老师发现有部分同学在画图思考，你们的研究有突破吗”，这是教师的第一次引导，目的非常明确，就是引导学生把注意力集中到画图策略的运用上，避免学生空想、胡乱猜测等无目的学习行为发生，从而提高教学的有效性，为打造高效课堂服务。又如，“其实，第一位同学的画图也是可以的，只不过理解起来有难度，大家再想想就会有新的思路了”，教师提示学生研究问题的方法有很多，虽然方法有差异，但不是一无是处的，可能不太认可的方法反而闪现着智慧的光芒。正因为教师的肯定和认可，学生的思维不断发生碰撞，想到了将图意用等量关系式表达出来，这样的表示更加凸显问题的本质，能够提高学生的学习效率，也让他们的学习个性得到充分彰显。也许，这就是信任的魅力所在，也是信任的力量所在。

2.鼓励特立独行

特立独行不是指学习的另类，而是学习个性的彰显。因此，在组织学生探究时，教师要鼓励学生大胆思考，从不同的方向、不同的角度去分析与解决问题，实现学习的突破。首先，营造宽松自由的氛围，让质疑成为点燃思维的导火索。课堂上，教师没有把学生的学习活动局限在一个范围内，而是让他们尽其所思、想其所想，助推学生的思维发生碰撞，激发学生的灵感。于是，就有学生大胆质疑：“老师，这道题是不是出错了，一会儿果汁，一会儿玻璃壶的，两个问题好解答吗？”这时，就会有更多的学生敢于发表自己的观点，如“这道题中有两个不同的问题，还真是不好解决啊”等。质疑和困惑有时并不是学习的真正难点，学习的真正难点是没有思路，没有点燃思维的星星之火，而质疑恰好是点燃星星之火的火种。其次，创设适宜的探究情境，促使学生迸发出思维的火花。如上述教学中，学生产生疑惑，这是最需要点拨的时候。教师根据学生的表现，问道：“老师发现有部分同学在画图思考，你们的研究有突破吗？”这看似是对学生学习进展的询问，实质上是给予学生更多的启迪，让他们意识到画图策略是一种不错的选择，如此才有了后续教学中的那份精彩与绚丽。

当然，这期间并非一帆风顺的，有些学生还是不知从何处下手解题。如有学生发出这样的感慨：“我也试着画图，但是感觉难以画清楚，因为既要画玻璃壶，又要画果汁。”这样教学既让学生意识到用画图策略解决问题并非万能的，甚至效果是不明显的，又能激发学生的探究意识：“老师都认可的画图策略，为什么你会这样说呢？我偏不信这个邪，我要通过画图好好地研究这道题。”也许，这就是学生继续画图思考、继续进行小组交流的动力所在吧！

3.不断引导反思

反思对于学生的数学学习大有裨益，正因为学生对问题不断反思，才会从中获得启发，找到问题解决的关键，迸发出研究、分析问题的灵感。在不同的思维碰撞中，学生对画图策略的运用会更加熟练，会逐步掌握解决问题的要领。如课堂上第一批学生呈现的示意图，图意清晰，给人一目了然的感觉，尽管他们难以清楚地阐述其中蕴含的数量关系，但对于其他学生的思考有很大的促进作用。紧接着，第二批学生呈现示意图，他们不仅改变了原先的图示，而且对各种数量关系的表述也更加清晰、有条理，他们对图示的解读就成为解决问题的关键。如“这时我们发现玻璃壶是一样的，它在每一次的称重中都是固定不变的……”这样的解读，不仅是打开思维困局的“金钥匙”，更是点燃思维的星星之火。因此，我们看到了可喜的一幕：学生不仅自己能把这道“倍量关系”题解读得非常清晰，而且可以给其他学生的学习提供思维指引，从而出现了更多精辟的分析，如“从图中可知，就是把相同的部分去掉，多出来的2杯果汁就是总重量的差，即240克，那么一杯果汁就是120克”等。不难看出，引领学生对一些解决问题的关键之处进行反思，能够收获不一样的精彩。

4.鼓励总结提炼

古语云“学而不思则罔”，这说明了学生的数学学习需要思维做支撑。这样学生才能在思考中理解、在理解中内化，并在反思中明晰数学知识的本质，实现学习的突破，使数学学习愈发灵动、富有生机。因此，在数学课堂中，教师不仅要教授解决问题的基本方法与策略，还要重视问题探究过程中的思维启发，引导学生深入理解其中的数学思想方法，挖掘学生的潜能。同时，教师还要帮助学生积累相关的数学活动经验，为他们的持续学习、探究提供动力支持。

（1）鼓励反思，举一反三

上述教学，教师引导学生用画图策略解读与分析问题，并在学生的思考中逐步渗透数学思想方法，为学生数学素养的提升提供了有意义的“养料”。同时，教师还引导学生进行必要的学习梳理，以此加速学生的学习进程，使学生的数学学习更具智慧。如在图示分析与研究的基础上，教师鼓励学生进行深入探究，拓展学生的学习视角，使学生习得了更多的数学知识。有学生就提出“我感觉到用文字来思考也很方便：玻璃壶+3杯果汁=580（克），玻璃壶+5杯果汁=820（克），这样就会发现820-580=240（克），实际上就是2杯果汁的重量，即一杯果汁的重量是120克”“将画图与文字表达结合起来，也会让问题研究容易些”等思考。这样通过反思，学生学会举一反三，完善了自己的认知。

（2）引导提炼，总结规律

数学课堂中，教师既要重视对学生反思的引导，使学生完善自己的知识体系，又要教会学生总结提炼的方法，帮助学生掌握规律和积累数学活动经验。如上述教学，教师指导学生比较不同的图示，引发学生更为深入的思考，并组织学生进行辩论，使学生对“倍量关系”问题的本质愈发明晰。通过对学习过程进行反思，学生明白解决“倍量关系”问题的本质就是把握住变量和不变量：首先剔除不变量，明确前后数量的变化是由变量引起的；其次，梳理总结其中的规律，找出问题解决的关键；再次，形成规律和有效的数学思维方式，使学生的数学学习更理性，充溢着思考的活力。

总之，教师要从整体上布局，善于用整体的观点组织和设计教学活动，努力让每一个学生成为知识的探究者、问题的研究者，使他们积极投身于数学探究之中。同时，教师在教学中要因势利导，切实做好学生学习的引领者，适时启发他们探寻现象背后的奥秘，引导他们进行更加深入的思考，使他们的数学学习更有灵性、更富智慧。