轨迹和干扰功率联合优化的无人机主动窃听算法

周洁， 王培臣， 张孟杰， 赵睿

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

由于低成本、高机动性等特点，无人机(UAV)在公共安全、灾害管理、监视和通信等方面的应用需求不断增长，特别是利用无人机支持地面蜂窝网络受到了广泛的关注[1].与地面无线系统相比，在无人机辅助无线通信系统中，无人机可以灵活、快速地进行部署[2]，为无基础设施覆盖的设备提供一种具有前景的视距链路(LoS)连接技术[3]，进而可以获得更高的可达速率.

然而，随着无人机通信系统的普及，低成本的无线服务扩大了罪犯或恐怖分子的活动范围，对国家安全产生了严重的威胁[4].因此，政府机构需要合法地监控任何可疑的通信链接，并检测商业无线网络中的异常行为.文献[5]研究一种由3架无人机组成的无线监控系统，1架无人机作为合法的窃听者，采用干扰技术主动窃听其他两架无人机的可疑通信，综合考虑有效窃听速率和无人机能耗，提出一种迭代干扰功率优化算法分配干扰功率和中继功率.文献[6]构建3架无人机组成的无线监控系统，合法无人机通过跟踪可疑无人机的飞行，防止故意犯罪和恐怖袭击，为了提高跟踪精度，合法无人机综合利用可疑发射器信号的窃听数据包、到达角和接收信号强度，提出了一种新的跟踪算法.文献[7]考虑一种地面主动窃听无线信息监视场景，1个合法窃听器试图窃听由无人机可疑发射器发送的可疑信息，提出一种基于连续凸逼近的迭代算法求解原非凸优化问题[8]，从而最大限度地提高可达窃听速率.

在目前的研究中，主动窃听器被视为固定在地面的节点，或是固定飞行路径的无人机，无人机作为主动窃听器的轨迹变化对系统窃听速率的影响几乎被忽略.然而，无人机的轨迹优化问题在无人机网络中至关重要，这是因为无人机的高机动性、无线通信固有的广播特性，以及考虑的信道是由视距链路控制的，无人机的位置变化可直接影响其接收速率.基于轨迹优化的无人机通信模型受到了学者广泛的关注.文献[9]在地面存在多个用户及多个窃听者的情况下，部署单个无人机对地面用户进行服务，通过一个干扰无人机对地面窃听者进行干扰，提出无人机轨迹和发射功率联合优化算法，从而使所有用户的平均安全速率最大化.文献[10]在以无人机为移动中继的无线通信系统中，采用无人机中继在两个地面用户之间转发信息，地面上存在一个窃听者对中继无人机进行窃听，提出基于机动性约束、无人机功率约束和中继无人机信息因果约束的安全速率最大化问题，利用更新速率辅助块坐标下降，并采用连续凸逼近技术交替优化两种无人机的发射功率和飞行轨迹.文献[11]在位置区域不确定的多个窃听者的情况下，研究向多个合法接收方发送机密信息的无人机通信系统.基于此，本文研究无人机的轨迹变化对系统有效窃听速率的影响，并进行轨迹和干扰功率的联合优化.

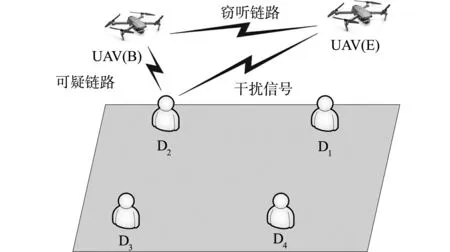
图1 无人机主动窃听通信系统模型Fig.1 Proactive eavesdropping communication system model of UAV

1 系统模型

在一个三维笛卡尔坐标中，无人机B(UAV(B))是一个可疑发送节点，发送可疑信息到M个地面用户Dm，m∈≜{1，2，…，M}，地面用户和UAV(B)均只配备一根天线.无人机E(UAV(E))是一个合法窃听器，配备两根天线，分别用于窃听从UAV(B)发送到地面用户的信息，以及发送干扰信号干扰地面用户.UAV(E)可以通过自干扰消除技术，消除自身发送的干扰信号[12].无人机主动窃听通信系统模型，如图1所示.

两架无人机假设在一个恒定的高度H飞行，这是无人机需要地形回避的最小值，同时，也有助于减少其上升或下降时的能源消耗.UAV(B)采用时分多址(TDMA)的传输方式服务地面用户[13]，即每个时隙只服务于一个用户，UAV(B)根据距离最近原则，选择服务的用户.为了简化优化问题，确保地面用户的接收速率最大化，UAV(B)的轨迹和用户调度规则A已定，而UAV(E)的初始轨迹是以用户的几何中点为圆心，设置不同飞行半径的圆形轨迹.

设无人机的整个飞行周期为T，连续时间意味着无穷多个速度约束，这使无人机的轨迹设计难以处理.因此，将T离散化，等分为N个很小的通信时隙长度δt，即T=Nδt.由于每个通信时隙设置得足够小，所以可认为在每个时隙中，无人机的坐标位置不变.

利用离散化的时隙，可将无人机的二维水平坐标表示为

qv[n]≜[xv[n]，yv[n]]T，n∈N≜{1，2，…，N}，v∈V≜{B，E}.

上式中：V为无人机B，E的集合.

定义M个地面用户Dm在三维笛卡尔坐标上的水平坐标为

qDm≜[xDm，yDm]T，m∈≜{1，2，…，M}.

为计算方便，忽略无人机起飞和降落的时间.UAV(B)和UAV(E)的最大飞行速度为vmax，则无人机在每个时隙的最大飞行距离L=δtvmax.此外，UAV(B)，UAV(E)的最后一个时隙会飞到初始位置.

根据上述假设，UAV(B)的轨迹已定，只需考虑UAV(E)的移动约束，有

‖qE[n+1]-qE[n]‖2≤L2， ∀n，

(1)

qE[1]=qE[N].

(2)

为了避免UAV(B)和UAV(E)在飞行过程中发生碰撞，增加最小安全距离的约束，即

(3)

式(3)中：dmin为UAV(B)，UAV(E)之间的最小安全距离.

在文中的无人机-地面通信的无线通信系统中，假设UAV(B)，UAV(E)与所有地面用户的信道都为视距链路，在第n个通信时隙中，UAV与地面用户的信道模型hv，Dm[n]为

(4)

式(4)中：β0为参考距离d0=1 m时的信道功率增益；dv，Dm[n]为第n个时隙无人机与地面用户的距离.

UAV(B)与UAV(E)之间的信道模型hB，E[n]为

(5)

式(5)中：dB，E[n]为第n个时隙UAV(B)与UAV(E)之间的距离.

UAV(E)的干扰功率约束为

0≤PE[n]≤PE，max， ∀n.

(6)

式(6)中：PE[n]为第n个时隙UAV(E)的干扰功率；PE，max为UAV(E)的干扰功率峰值.

第n个时隙UAV(E)的接收速率RE[n]为

(7)

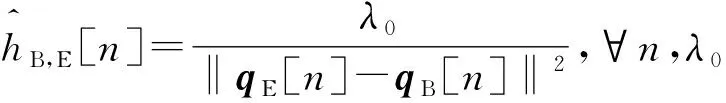
(8)

第n个时隙地面用户Dm的接收速率RDm[n]为

(9)

由于UAV(E)工作于主动窃听模式，当RDm[n]≤RE[n]时，UAV(E)能可靠地解码来自UAV(B)的消息，此时，有效窃听速率的值为RDm[n]；当RDm[n]>RE[n]时，合法窃听器UAV(E)无法无差错地解码信息，此时，有效窃听速率为0.

因此，合法窃听器UAV(E)的有效窃听速率REV[n]为

(10)

2 优化问题

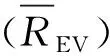
优化问题P1可表示为

(11)

由优化问题P1可知以下两点结论.

1) 在优化目标中，RDm[n]和RE[n]的分子、分母都含有轨迹及干扰功率的优化变量.

2) 因为优化变量在所有时隙上的耦合性，无法使用标准凸优化技术进行求解，因此，优化问题P1无法使用标准的凸优化技术进行求解，故先将其分解为优化UAV(E)的干扰功率、优化UAV(E)的轨迹两个子问题，再交替求解这两个子问题，直到算法收敛.

2.1 UAV(E)干扰功率的优化

引入松弛变量ηpo对非凸问题进行替代简化，通过Xm={xm[n]，∀m，n}，Ym={ym[n]，∀m，n}，将优化问题P1转换为优化UAV(E)干扰功率的子问题P2，即

(12)

(13)

(14)

(15)

0≤PE[n]≤PE，max， ∀n，

(16)

αm[n]RDm[n]≤RE[n]， ∀m，n.

(17)

由式(12)～(17)可知，子问题P2是非凸约束，表示为两个凸函数差的形式，可以采用逐次凸优化(SCA)技术进行求解，即采用一阶泰勒展开式近似eym[n].

(18)

因此，子问题P2可重新表示为子问题P3，即

(19)

子问题P3是一个凸优化问题，可直接采用现有的凸优化求解工具(如CVX)进行求解.

2.2 UAV(E)轨迹的优化

引入松弛变量ηtr，通过Xm={xm[n]，∀m，n}，Ym={ym[n]，∀m，n}，将优化问题P1转换为优化UAV(E)轨迹的子问题P4，即

(20)

(21)

(22)

(23)

‖qE[n+1]-qE[n]‖2≤L2，n∈N≜{1，…，N}，

(24)

qE[1]=qE[N]，

(25)

(26)

αm[n]RDm[n]≤RE[n]， ∀m，n.

(27)

由于式(22)，(23)，(26)，(27)是非凸约束，因此，子问题P4是一个非凸优化问题.

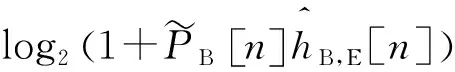
(28)

(29)

因此，式(22)，(27)可近似表示为

(30)

(31)

由于非凸约束是两个凸函数差的形式，可以采用连续凸优化技术进行求解，即采用一阶泰勒展开式近似eym[n]，并引入松弛变量∂={∂m[n]，∀n，m}，将式(23)重新表示为

(32)

对非凸约束引入松弛变量γ={γ[n]，∀n}，式(26)可重新表示为

(33)

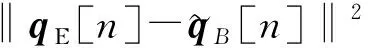
(34)

(35)

经上述变换，将子问题P4中的非凸约束转换为凸约束，可得子问题P5，即

(36)

子问题P5是一个凸优化问题，可直接采用现有的凸优化求解工具(如CVX)进行求解.

3 整体算法

在经典块坐标下降法中，为了保证算法的收敛性，需要在每次迭代中以最优的方式精确求解更新每个子问题[14].然而，在求解过程中，对于子问题P2，P4，只优化解决近似问题P3，P5.因此，无法直接应用经典块坐标下降法的收敛性分析[15].

优化问题P1的交替优化算法(算法1)有如下6个步骤.

算法1交替优化.

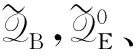
步骤2循环.

步骤3开始，k=k+1，γ=γ/(1+(k-1)×ζ).

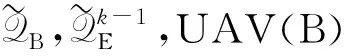
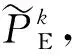
步骤6直至优化问题P1中目标值的增加小于阈值ξ.

文献[15]已验证了算法1的收敛性，不再赘述.

4 数值结果与分析

通过仿真验证轨迹和干扰功率联合优化算法(文中算法)的有效性.采用以下两种基准算法作为比较:1) 算法1，固定发送功率的UAV(E)轨迹优化；2) 算法2，固定UAV(E)轨迹的干扰功率优化.

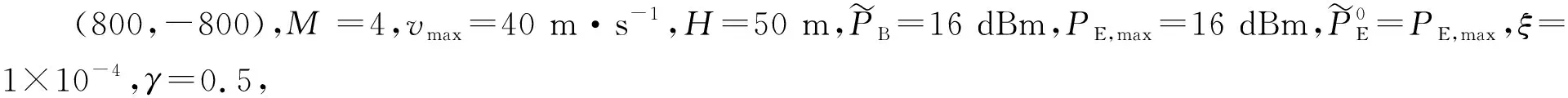
当T=160 s时，UAV(B)的用户调度规则，如图2所示.图2中：D1～D4分别为地面用户1～4.由图2可知：为了最大化地面用户的可达接收速率，UAV(B)的轨迹是在用户上空的正方形飞行轨迹，并逐个服务于距离最近的一个用户，即UAV(B)每个时隙只服务一个用户[11].UAV(E)的初始轨迹是一个以原点为圆心，半径为600 m的圆形.

UAV(B)和UAV(E)的轨迹，如图3所示.由图3可知：UAV(B)以固定的轨迹在每个用户上方进行逐个访问，UAV(E)优化后的轨迹与UAV(B)的轨迹相似，从而实现对UAV(B)发送信息的窃听.

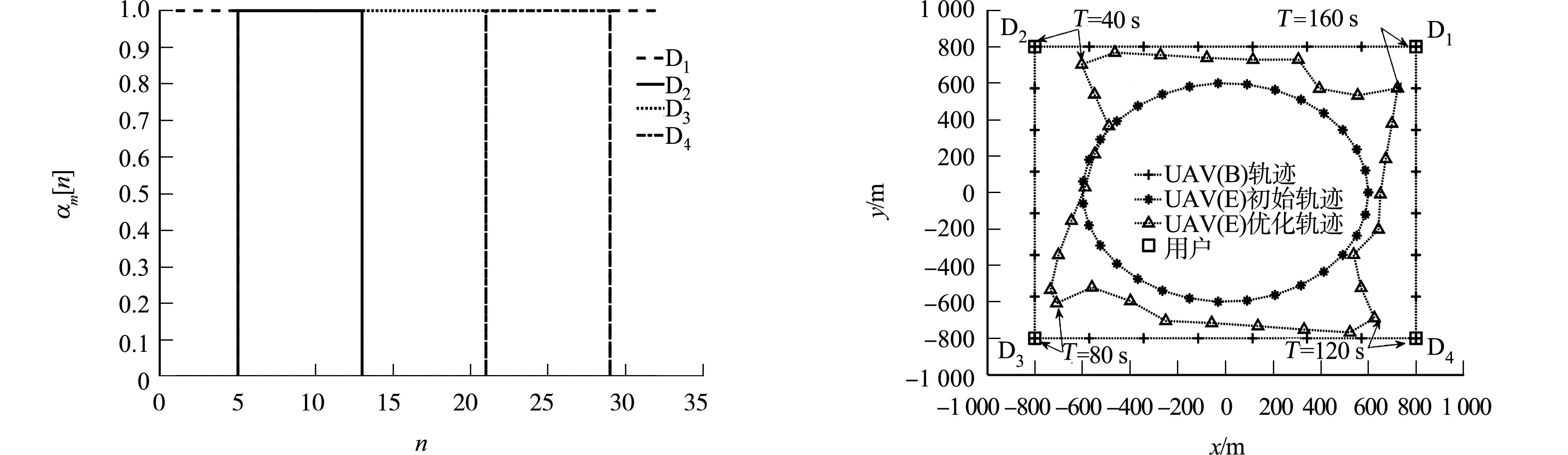
图2 UAV(B)用户调度规则 图3 UAV(B)和UAV(E)的轨迹 Fig.2 User scheduling rules of UAV(B) Fig.3 Trajectory of UAV(B) and UAV(E)

UAV(E)的干扰功率随时间的变化情况，如图4所示.由图3，4可知：当T分别为0，40，80，120，160 s时，对应的UAV(B)，UAV(E)飞行到各地面用户上空位置，其中，UAV(E)距离地面用户较近，为了使有效窃听速率最大化，所以UAV(E)发送的干扰功率下降.

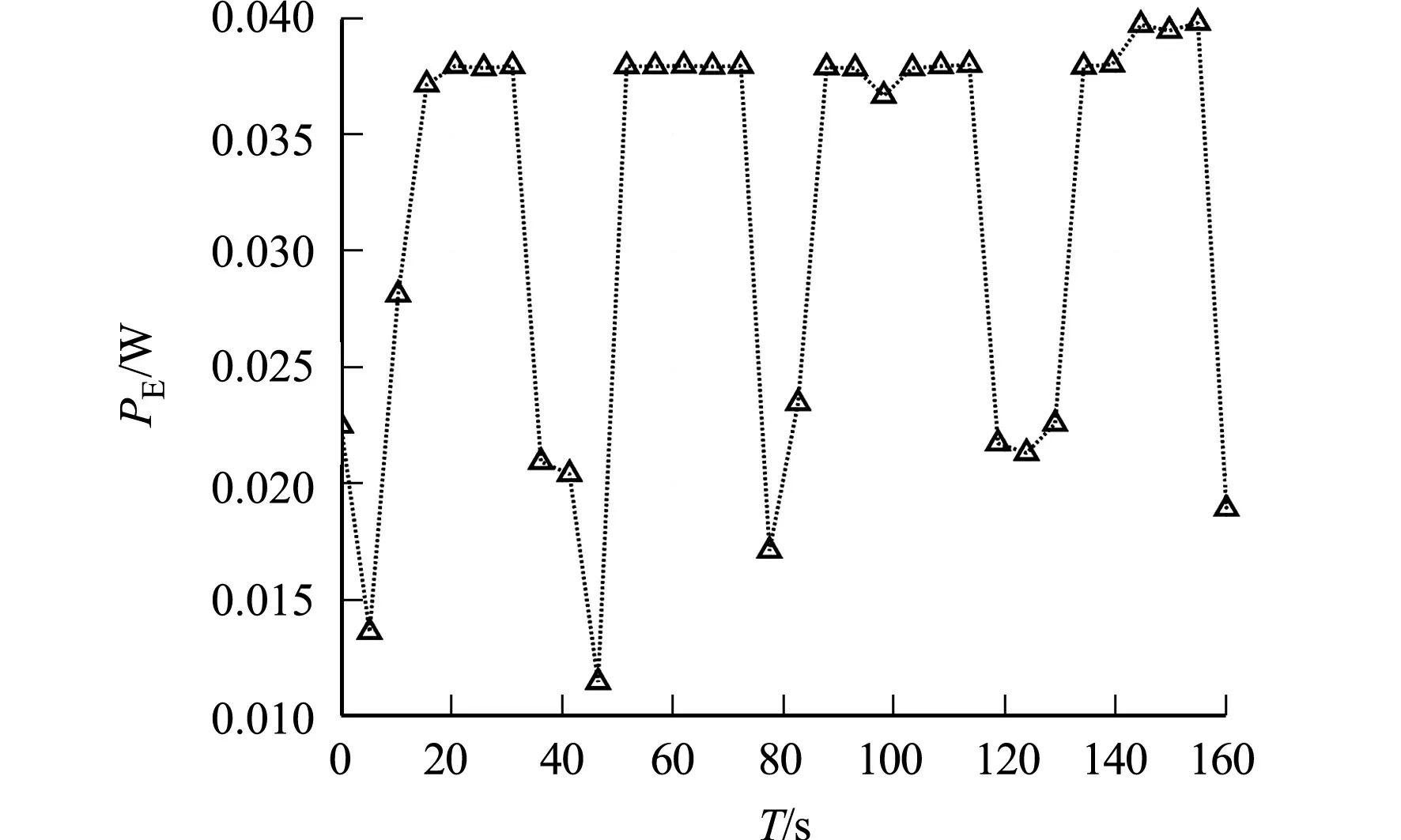
图4 UAV(E)的干扰功率随时间的变化情况Fig.4 Variation situation of interference power with time of UAV(E)

UAV(E)的平均接收速率，如图5所示.由图5可知：文中算法明显优于算法1，2，这就验证了UAV(E)轨迹和干扰功率的联合优化可以提高有效窃听速率；相比较于算法2，文中算法的平均接收速率明显提高.

由于固定的轨迹限制了UAV(E)机动性的潜力，而当轨迹和干扰功率联合优化时，在单纯的轨迹优化上叠加了功率的优化，使UAV(E)更加灵活.因此，相较于算法1，2，文中算法的UAV(E)平均接收速率更高.随着飞行周期T的增大，UAV(E)具有更大的移动范围，给UAV(E)靠近UAV(B)提供了可能，故UAV(E)的平均接收速率随着飞行时长T的增大而增大.

当T=160 s时，文中算法平均有效窃听速率收敛图，如图6所示.由图6可知：随着迭代次数的增加，文中算法的平均有效窃听速率迅速增加，约18次迭代后，平均有效窃听速率收敛到一个常数，即最大有效窃听速率.

图5 UAV(E)的平均接收速率 图6 文中算法平均有效窃听速率收敛图Fig.5 Average reception rate of UAV(E) Fig.6 Convergence graph of average effective eavesdropping rate of proposed algorithm

5 结束语

对采用无人机合法窃听器的无人机空对地通信系统的物理层安全问题进行研究.采用无人机合法窃听器对可疑链路进行窃听，针对可疑系统的特点，在给定的飞行周期内，对主动窃听无人机进行轨迹和干扰功率联合优化，从而最大限度地提高合法窃听器的有效窃听速率.将非凸的优化问题分解为两个容易处理的子问题，利用更新速率辅助的块坐标下降和连续凸优化技术，采用一种高效的迭代算法，交替求解子问题，并利用SCA技术解决相关的优化问题.相较于固定发送功率的UAV(E)轨迹优化(算法1)、固定UAV(E)轨迹的干扰功率优化(算法2)这两种基准算法，文中算法可以显著地提高系统的性能.在今后的工作中，将进一步考虑不同带宽之间的动态分配，以及在用户位置不完全可知的情况下空中存在多个移动窃听者的情况.