采用特征预处理ICP算法的机器人运动环境建图
申鸿, 李平, 贾丙佳
(华侨大学 信息科学与工程学院, 福建 厦门 361021)
移动机器人应用领域的拓展对机器人环境认知能力和自主规划能力提出更高的要求.其中,机器人的环境认知能力是自主规划能力的保障.机器人的环境认知过程即地图的构建与定位过程,同步定位与地图构建(SLAM)技术要求机器人从初始位置出发(未知或已知),通过传感器实时收集环境信息,构建地图并实时更新机器人位姿[1].机器人的环境认知在硬件上依赖于各式传感器,常用的传感器主要有激光测距仪、声纳和视觉传感器等.由于精度高、环境适应性强、扫描范围广等优势,激光测距得到了广泛的应用[2].因此,文中选用激光雷达作为传感器进行数据采集.
SLAM的首要任务是研究传感器数据帧之间的变换关系.针对激光雷达传感器,SLAM研究各帧激光点云数据之间的变换关系,即点云数据配准问题.国内外学者已经针对该问题进行大量的研究.文献[3]提出的迭代最近点(ICP)算法原理简洁、配准精度高,但对待配准的两帧点云数据的初始误差敏感,且未包含局部特征信息[4].此外,激光雷达扫描获得的两帧点云数据无法保证每个点一一对应,帧与帧的数据点数量并不严格相等,应用ICP算法时存在一对多、多对一等问题,对算法精度和算法迭代次数有较大的影响[5-6].针对数据缺失问题,文献[7]提出一种特征点ICP配准方法,通过控制特征点在点集配准过程中的权重,提高点集的配准精度.文献[8]针对扩展卡尔曼滤波-同步定位与地图构建(EKF-SLAM)中由方向方差引起的一致性问题,提出一种融合绝对方向信息的EKF-SLAM算法,有效地校正了无人车的累计误差问题.文献[9]为改善二维点云配准精度,降低对初始位置的敏感性问题,提出一种利用聚类改进的ICP算法.文献[10]提出一种点到线的ICP算法,以解决扫描点单映射问题.基于此,本文结合室内环境建图的典型特征,提出一种特征预处理ICP算法.
1 机器人运动环境建图
激光雷达通过激光扫描一周(360°),测量环境点到激光雷达所在位置的距离,记录对应的角度,并将每一周测量的数据作为一帧数据.这些距离数据和角度数据可用于环境地图的创建,准确地描述环境情况.然而,使用激光雷达对环境进行扫描时,受到硬件性能的限制(如最大扫描距离等),每帧数据仅包含整体环境的部分数据.因此,在对全局环境建图的过程中,移动机器人需要不断运动,以获得若干帧激光雷达数据,并使这些数据点集能够完整地包含整体环境信息.
基于激光雷达数据的地图创建过程可分为数据采集、数据配准、地图创建3个步骤.由于每次扫描得到一帧数据的坐标都是定义在以激光雷达位置为原点的坐标系下,而激光雷达随着机器人运动发生位姿(位置和角度)的改变.因此,在机器人运动过程中采集到的每帧数据都处于不同的局部坐标系,必须将所有的数据点集配准到同一全局坐标系.数据帧差异示意图,如图1所示.图1中:xM0-yM0为位置M0所处的局部坐标系;xM1-yM1为位置M1所处的局部坐标系;R为机器人.随着机器人的运动,位置M0,M1采集的两帧数据会产生旋转和平移.

(a) 机器人 (b) 位置M0 (c) 位置M1图1 数据帧差异示意图Fig.1 Schematic diagram of data frame differences
针对机器人运动过程中的建图问题,在数据采集后,需要进行数据配准.数据配准是对每帧扫描数据点集进行配准操作,求取不同局部坐标系之间的变换矩阵.完成数据配准后,根照计算得到的变换矩阵,对不同数据帧进行平移、旋转操作,使其集中于同一全局坐标系下,完成机器人环境地图的创建.
2 扫描配准方法
2.1 移动机器人扫描配准方法
扫描配准方法是一种适用于未知环境的迭代方法[7].扫描配准方法对连续采集的相邻扫描数据帧进行配准,得到相对位姿的变换关系,增量性地更新机器人的位姿和环境地图,具体有以下4个步骤.
步骤1扫描数据集合(待配准点集)记为P,上一时刻扫描数据集合(参考数据点集)记为Q.
步骤2通过扫描配准方法,计算由待配准点集P配准到参考数据点集Q的位姿变换矩阵(R,T).其中,R为旋转变换矩阵;T为平移变换向量.
步骤3假设k时刻,机器人位姿为pk=(xk,yk,θk).根据位姿变换矩阵(R,T),计算当前位姿变换量(Δxk,Δyk,Δθk),并更新机器人的位姿,得到k+1时刻机器人的位姿为pk+1.
步骤4将待配准点集P记为新的参考数据点集Q,转步骤1进行迭代计算.
扫描配准方法有多种实现方式,但ICP算法最常用.
2.2 ICP迭代算法
ICP算法在点云配准领域应用广泛,是一种直接的点云配准方法.首先,ICP算法对待配准点集中的每个点搜索参考数据点集中对应的最近点,并将这些点记为若干组点对.然后,通过最小二乘法极小化点对误差函数,计算其对应的旋转变换矩阵R和平移变换向量T.最后,进行迭代,将待配准点集按照旋转变换矩阵R和平移变换向量T进行旋转、平移变换, 并判断变换后的点集与参考数据点集的误差是否满足要求,若不满足,则继续迭代.
ICP算法流程图,如图2所示.图2中:qi(i=1,2,…,n)为参考数据点集中的第i个点;pj(j=1,2,…,m)为待配准点集中第j个点;d(qi,pj)为从点qi到点pj的距离.由图2可知:ICP算法的实现依赖于待配准点集与参考数据点集的一一对应.ICP算法实现的难点在于如何找到相应的关联点对[11].ICP算法假设待配准的两组扫描点完全重叠,而实际应用中由于激光雷达扫描误差等原因,无法满足该条件.因此,ICP算法必然会产生部分错误点对,同时,由于激光雷达的离散测量特性,不存在真正配准的两个对应点,即所有对应点都是近似配准的.由此可知,上述问题影响了ICP算法的精度.

图2 ICP算法流程图Fig.2 Flow chart of ICP algorithm
此外,ICP算法还要求待配准点集与参考数据点集具有一定的重合度,即对迭代初值有较高的要求.在应用ICP算法的过程中,若迭代初值选择不当,会导致迭代无法收敛到全局最优结果[12],从而导致配准失败.
3 特征预处理ICP算法的地图创建
针对ICP算法在激光雷达数据扫描配准过程中存在的问题,提出一种特征预处理ICP算法(文中算法).首先,根据扫描的数据特征进行机器人位姿的粗配准,以降低迭代初值;预处理过程根据扫描数据的角度信息生成特征柱状图,根据特征柱状图进行方向配准与位置配准.然后,针对激光扫描数据存在噪点的问题进行扫描点过滤,使点集一一对应,进行ICP算法精配准.
特征预处理ICP算法流程图,如图3所示.

图3 特征预处理ICP算法流程图Fig.3 Flow chart of ICP algorithm for feature preprocessing
3.1 数据采集
采用RPLIDAR A1M8型激光雷达(上海市思岚科技公司)采集数据.激光雷达(图4)的测距范围典型值为0.15~12.00 m,扫描角度为360°,测距分辨率典型值为0.5 mm,角度分辨率典型值为1°(5.5 Hz扫描时),扫描频率典型值为5.5 Hz,最大值为10.0 Hz.当激光雷达工作于典型值时,扫描一次恰好有360个采样点.
将激光雷达返回的二维环境扫描数据记为集合O={(θi,ρi)|i=0,…,n},θ为采样点的角度,ρ为采样点与激光雷达的距离.激光雷达相邻扫描数据帧,如图5所示.图5中:蓝色点为参考数据点集;红色点为待配准点集;X-Y为全局坐标系.相邻两帧扫描数据发生了较多偏离,且不能严格实现点与点之间的一一对应.因此,无法利用ICP算法中的最邻近方法(将两帧数据中曼哈顿距离最小的点对作为对应点)确定对应点.

(a) 正面 (b) 底面 图4 激光雷达实物图 图5 激光雷达相邻扫描数据帧 Fig.4 Physical map of lidar Fig.5 Lidar adjacent scan data frames
3.2 特征预处理粗配准
在室内环境下,激光雷达扫描数据可以获得较明显的环境特征,如墙体对应的直线特征数据、墙角对应的角点特征数据等.文献[13]利用数据中的特征点构建三角形结构,并进行点集筛选.文献[14]提出一种基于点云法向量间夹角特征的ICP算法,提高了配准效率.文献[15]采用边界特征点云信息结合聚类分析的配准方法.然而,由于移动机器人平台计算能力具有局限性,因此,对配准算法的计算量和可靠性提出了更高的要求.
针对两帧数据有较大偏移的问题,利用环境特征进行角度柱状图和位置偏移量的粗配准.粗配准过程分为角度柱状图配准(方向配准)和位置配准,分别确定传感器的角度偏移量Δθ1和位置偏移量Δx1,Δy1.粗配准具体有以下3个步骤.
1) 角度集的计算.将激光雷达扫描的数据集O={(θi,ρi)|i=0,…,n}转换到直角坐标系下,有
(1)
并将集合记为P={(xi,yi)|i=1,…,n},即待配准点集.
对待配准点集P中的元素进行运算,有
(2)
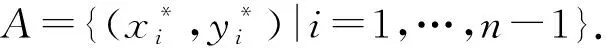


(a) 参考数据点集 (b) 待配准点集 图6 相邻数据帧的角度柱状图Fig.6 Angle histogram of adjacent data frames
2) 角度集的配准.根据计算可得参考数据点集和待配准点集的角度柱状图,由角度柱状图可知,典型墙体直线特征处角度柱状图数值较大,且激光雷达的位姿变换对角度柱状图的影响呈平移趋势.由于低成本激光雷达本身的精度及环境干扰等因素,平移后的角度柱状图不一定能够完全重合.因此,角度集应按最小化进行配准,以找到最合适的平移数N,使两帧数据的角度柱状图平移后尽量重合,误差最小化公式为
(3)

由式(3)可得两个角度柱状图平移后误差最小时的平移数N,并得到角度偏移量Δθ1=0.15N,从而对待配准点集进行旋转操作.
3) 位置配准.完成旋转操作后,两帧数据角度误差已经控制在0.15 rad内,可近似认为两点集仅需进行平移操作即可重合.因此,分别计算两帧数据的横、纵坐标均值,计算平均坐标差值,根据差值对当前扫描点进行平移,有
(4)
(5)
式(4),(5)中:xj,yj为参考数据点集中的第j个元素.
3.3 扫描点过滤
经过特征预处理粗配准后,待配准点集与参考数据点集的误差控制在较小范围内,迭代初值较小,但待配准点集与参考数据点集中点的个数仍不一致.为了获得较高的配准精度,进行扫描点过滤具有必要性.若能确保待配准点集与参考数据点集中的点对一一对应,则有利于降低配准误差.扫描点过滤的过程如下.

(6)
并将参考点集最近点的序号记为js.
经过特征预处理粗配准后的两帧数据已具有一定重合度,因此,在找到第1对距离最近的配准点对后,即可依次逐步寻找第is个配准点对.迭代公式为
(7)

图7 欧式距离矩阵的构造Fig.7 Construction of Euclidean distance matrix
由于数据存在一定的重合度,此处仅搜索上一步得到的最近点附近的3个点,以减小计算量,且不影响后续剔除步骤.欧式距离矩阵的构造,如图7所示.
2) 序列对应关系的判别和过滤.对于两帧数据的对应关系,存在3种情况:ⅰ) 情况1,待配准点集与参考数据点集一一对应;ⅱ) 情况2,待配准点集与参考数据点集存在多对一问题;ⅲ) 情况3,待配准点集与参考数据点集存在一对多问题.3种情况的欧式距离矩阵,如图8所示.
(a) 情况1 (b) 情况2 (c) 情况3图8 3种情况的欧式距离矩阵Fig.8 Euclidean distance matrices of three situations

对于多对一与一对多问题,可以对相应集合中的冗余点进行过滤操作.首先,判断冗余点是否超过激光雷达的误差范围,舍弃超出误差范围的点,保留不超过误差范围的点.然后,对存在不一一对应问题处的保留点计算平均值,以消除噪声带来的误差,求得新点坐标的计算公式为
(8)
式(8)中:(xc,yc)表示第c个不超过激光雷达误差范围的冗余点;l表示不超过激光雷达误差范围的冗余点的个数.
3.4 ICP配准
经过节3.2,3.3的数据处理后,参考数据点集Q和待配准点集P的长度完全一致,再应用ICP算法进行精配准,具体有以下4个步骤.
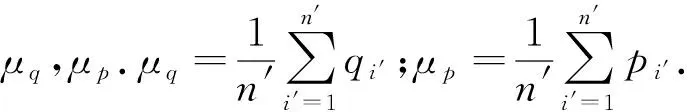
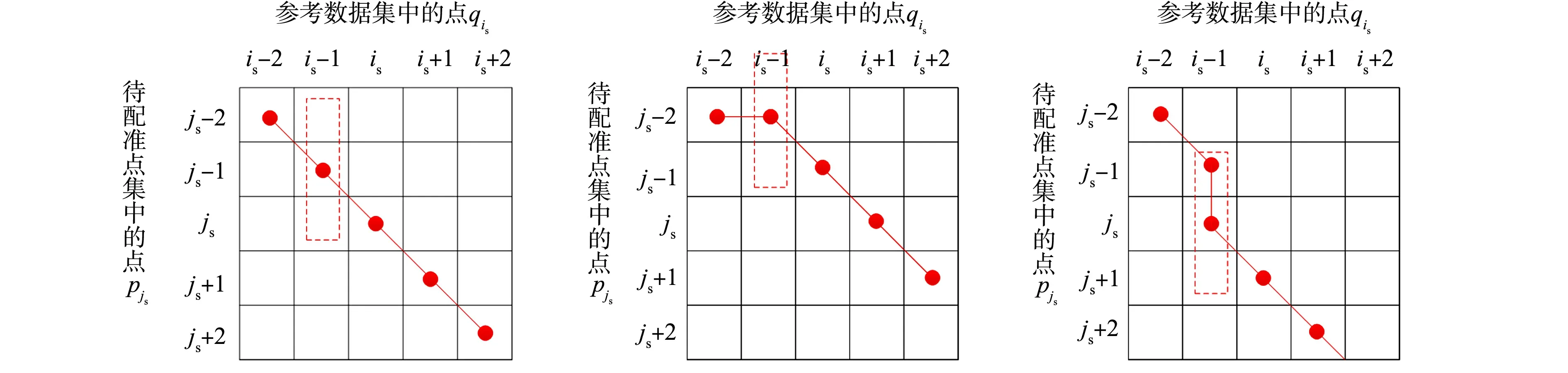
步骤2点云配准.对粗配准后的参考数据点集Q1中的点qi′计算搜索待配准点集P1中的点pi′,使点qi′到点pi′的距离d(qi′,pi′)最小,得到最邻近点对(qi′,pi′).
步骤3最小二乘优化问题计算.计算旋转变换矩阵的最小二乘优化问题,有
(9)
式(9)中:R*为使该式取值最小的参数.
根据上述最小二乘问题计算的旋转变换矩阵R,计算平移变换矩阵T,有
T=μq-Rμp.
(10)
步骤4误差判断迭代.通过步骤3计算得到的旋转变换矩阵R、平移变换矩阵T,对待配准点集进行变换,并判断误差是否达到阈值.
误差E(R,T)的计算公式为
(11)
若E(R,T)小于给定的阈值或达到迭代次数,则配准结束;否则,则回到步骤2进行下一次迭代.经迭代计算,可得旋转变换矩阵R和平移变换向量T,再与粗配准得到的角度偏移量Δθ1与位置偏移量Δx1,Δy1叠加,最终得到两帧数据的实际变化量(Δxk,Δyk,Δθk).
3.5 地图创建
经过节3.1~3.4的操作后,可将所有激光雷达扫描数据集中于全局坐标系下,从而得到环境地图.同时,在实验过程中发现若将初次扫描数据作为参考数据点集,以后每次都将待配准点集配准到该参考数据点集上,那么,随着机器人的移动,累计误差将越来越大,即两帧数据差距越来越大,这直接影响了配准效果.因此,采取增量式更新地图的方法,每次配准都将上一次扫描数据作为参考数据点集,将当前时刻扫描数据作为待配准点集,计算相邻时刻两帧数据的实际变化量(Δxk,Δyk,Δθk),再增量式地将每次扫描的数据进行平移和旋转,将点集配准至初次扫描点集上,最终获得较精确的配准结果.
4 实验结果与分析
实验平台为Inert(R) Core(TM) i5-4200U CPU,1.6 GHz主频和4.00 GB内存的笔记本电脑,安装Windows 10操作系统.实验数据来自RPLIDAR A1M8型激光雷达,使用Matlab软件对实验数据进行配准效果对比,采用相邻两帧扫描点集测试ICP算法和文中算法,配准结果对比图,如图9所示.图9中:蓝色点为参考数据点集;红色点为待配准点集.

(a) 原始数据 (b) ICP算法
由图9可知:激光雷达的相邻时刻环境扫描数据点并不具有一一对应关系;ICP算法在配准过程中陷入局部极小值,直到迭代次数上限跳出循环才停止,最终配准效果较差;文中算法粗配准和扫描点过滤后,可保证点集的一一对应,且数据差异已降低到较小范围;点集精配准后,两帧数据完全重合.
在实际环境中进行建图测试,结果如图10所示.

(a) ICP算法 (b) 文中算法 图10 实际建图结果对比图Fig.10 Comparison diagram of actual map creation results
由图10可知:ICP算法在建图后仍存在大量未配准点;文中算法的点集重合度显著高于ICP算法,说明文中算法配准精度高于ICP算法.
5 结束语
根据室内环境存在大量直线特征数据的特点,建立角度柱状图数据,依据角度柱状图中体现的特征信息对数据进行粗配准,该预处理方法运算量较小且能显著减小迭代初值,解决了ICP算法迭代初值要求高的问题.依据扫描数据的曼哈顿距离,构建矩阵剔除无效对应点,解决扫描点不满足一一对应关系的问题,提高了配准精度.增量式地将当前扫描点集进行配准、融合后,建立环境地图.实验结果验证了文中算法的有效性,且复杂度较低.今后将进一步优化无效对应点剔除方法,提高剔除效率,以更少的数据创建精确的环境地图,并对复杂室外环境及动态环境下的建图进行研究.

