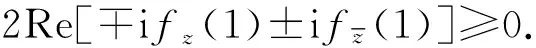调和映照与调和K-拟共形映照的边界Schwarz引理

李鸿萍

(华侨大学 数学科学学院， 福建 泉州 362021)

1 预备知识

由文献[1]可知：f在D上局部单叶、保向当且仅当其雅可比行列式Jf满足如下性质

定义f的拉普拉斯算子为

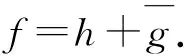
(1)

经典的Schwarz引理表明，对于D到自身内的解析函数f，若满足f(0)=0，那么，对于一切的z∈D有|f(z)|≤|z|.

经典的边界Schwarz引理如下.

定理A[3]假设f:D→D为解析函数，满足f(0)=0.进一步地，若f在z=1处解析且f(1)=1，那么下面的结论成立：

1)f′(1)≥1；

2)f′(1)=1当且仅当f(z)≡z.

定理A有如下推广.

定理B[4]假设f:D→D为解析函数，满足f(0)=0.进一步地，若f在z=α∈T处解析且f(α)=β∈T，那么下面结论成立：

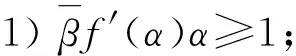
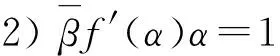
当α=β=1时，定理B与定理A是一致的.

解析函数的Schwarz引理是复分析的一个基本定理，有着深刻的几何背景，其研究受到了国内外许多数学家的关注，得到了大量的结果[1-17].调和映照作为解析函数的推广，如何将经典的Schwarz引理推广到调和映照上，近年来受到了国内外许多同行的关注，并得到了多种形式的估计，有些估计是精确的[6，9，15，18-19].边界Schwarz引理在经典平面复分析和多复变函数论上有着重要的应用.利用经典的边界Schwarz引理，文献[12]，[13]，[16]分别得到了规范的Rn空间上的凸和拟凸双解析映照的边界Schwarz引理.

首先，建立调和映照的精确的边界Schwarz引理.

定理1假设f为D到自身内的调和映照.若f在z=1处可微且满足f(0)=0和f(1)=1，那么，不等式

(2)

定理1可以被推广如下.

定理2假设f为D到自身内的调和映照.满足f(a)=0，这里a∈D.若f在z=α∈T处可微且满足f(α)=β∈T，那么，不等式

(3)

成立.

特别地，当a=0，α=β=1时，定理2与定理1一致.

假设f(z)为D到Ω⊆C上的单叶、保向调和映照，如果存在一个常数K≥1，使得

(4)

则称f(z)为调和K-拟共形映照.

调和拟共形映照是共形映照的推广，近年来围绕调和映照如何成为拟共形映照的问题吸引了许多同行的关注，得到了许多结果[20-24].另一个结果是建立调和K-拟共形映照的边界Schwarz引理，特别地，当K=1时，文中结果和定理A一致.

对于L>0，定义函数ΦL(s)为

ΦL(s):=μ-1(μ(s)/L)， 0

ΦL(0):=0，ΦL(1):=1.

上式中:μ(s)为Grötschz极值区域D[0，s]的模[24-25].称这样的ΦL(s)为Hersch-Pfluger偏差函数.这里的函数μ也可以表示成第一类椭圆积分，令

(5)

那么，

(6)

定理C[24]设K≥1，而f为D到自身上的K-拟共形映照，满足f(0)=0.那么，

|f(z)|≤P[ΨK](|z|)，z∈D.

(7)

式(7)中：

（1）注射剂量不准。高原牧区的环境较为恶劣，因此对于动物的防疫、注射通常是牧民自己动手，因为缺少专业的知识和经验，对于疫苗的剂量掌握不精确，甚至有些养殖户害怕动物因为疫苗产生应激反应，而人为减少注射的剂量，导致免疫效果低下。

(8)

为f的边界函数.进一步地，有

这里

(9)

为K的单调递增函数，满足

(10)

利用定理C可以得到调和K-拟共形映照的边界Schwardz引理如定理3.

定理3设f为D到自身上的调和K-拟共形映照.若f在z=1处可微且满足f(0)=0和f(1)=1，那么，

(11)

这里的LK由式(9)给出.

定理4设f为D到自身上的调和K-拟共形映照，满足f(a)=0，其中，a∈D.若f在z=α∈T上可微且f(α)=β，那么，

(12)

特别地，当a=0且α=β=1时，定理4与定理3一致.

2 主要定理的证明

定理1的证明：由文献[7]得到精确的估计式为

(13)

根据假设f在z=1处可微，可知

(14)

利用式(13)，式(14)可以改写成

于是有

(15)

式(15)中，令z=r∈(0，1)，并令r→1-，可得

(16)

于是有

下面证明精确性.考虑调和映照

对于极坐标下z=reiθ∈D，有

这意味着

所以，式(2)是精确的.证毕.

注2由定理1的证明可以得到等式

(17)

事实上，假设z=eiθ≠1，利用式(15)有

(18)

φa(p)=α，

且

由定理1可得

(19)

特别地，若a=0，那么，

(20)

证毕.

定理3的证明：由假设f在z=1处可微，所以f具有展开式(14).于是

(21)

取z=r∈(0，1)，并令r→1-，利用定理C得到

(22)

式(22)与式(2)表明

(23)

若K→1，那么LK→1且f为共形映照.因此，式(23)和式(17)表明

fz(1)≥1.

即经典的边界Schwarz引理.证毕.

φa(p)=α，

且

利用定理3的结论，得到

(24)

特别地，若a=0，那么

(25)

这里的M(K)由式(11)给出.

证毕.