寒冷地区高校教室冬季室内热环境与热舒适性分析

闫旭峰， 雷勇刚，， 景胜蓝， 尹晗硕

( 1. 太原理工大学 环境科学与工程学院， 山西 晋中 030600；2. 太原理工大学 土木工程学院， 山西 太原 030024 )

在美国采暖、制冷与空调工程(ASHRAE 55)标准中，热舒适被定义为人对所处热环境表示满意的心理状态[1].随着国家经济的迅速发展，人们生活水平得到显著提高，人们对室内热环境的要求越来越高，导致了暖通空调技术和设备的快速发展，同时也增加了能源的使用和温室气体的排放.因此，确定热舒适和节能之间的平衡已经成为一个世界性的挑战[2].对于学生来说每天大约三分之一的时间是在教室里度过.由于教室内学生的高密度聚集和不理想的室内热环境会直接对学生的学习和表现产生一定的负面影响，因此，在教室里提供舒适的室内环境是至关重要的.

迄今为止，国内外许多学者针对不同地区大学教室热舒适进行了大量的研究.Carolina等[3]在巴西某大学进行了热舒适调查研究，结果表明空调教室的最佳温度条件是23～24 ℃之间，超过20%的学生在22 ℃以下会感到不舒服，而且室内温度高达26 ℃不会对人体的热舒适性产生明显的影响.Kumar等[4]得出在自然通风的大学教室内，学生们更喜欢通过打开门窗或操作吊扇来维持室内舒适度，在室内空气温度为29 ℃时，吊扇的使用率超过80%.Fang等[5]研究发现香港空调教室学生的可接受温度下限低于ASHRAE标准.Mishra等[6]在埃因霍温工业大学的一个教室里进行了的热舒适研究，结果表明在近20 min的过渡后，参与者的最近一次热记忆的影响还较为显著，但随实验进行逐渐适应.刘佳璐等[7]研究发现西安某大学学生的热中性温度为20.6 ℃；热舒适温度范围为19.5～21.8 ℃.宁浩然等[8]对哈尔滨某大学教室进行热舒适研究，发现90%可接受的温度范围为19.7～23.2 ℃.姚润明等[9]通过对重庆大学自然通风教室热环境的研究，引入适应系数λ，提出aPMV(adaptive predicted mean vote)模型，使其结果更接近受试者的主观感受，并且减小了误差.

综上，前人主要是在有调节措施或环控设备的工况下对教室室内热环境开展研究，并主要在夏季进行.虽然关于教室热舒适的研究在过去几年里不断增加，但与一般的热舒适研究相比，寒冷地区大学教室热舒适研究的数量还比较少的[10]，尤其是在冬季供暖模式下的大学教室的研究更少.鉴于此，本文以寒冷地区太原市某大学供暖季教室为研究对象，对教室室内外热环境进行现场实测，同时对室内人体热舒适情况进行主观问卷调查.

1 研究对象与方法

1.1 调研对象概述

太原市位于山西省的中北部区域，东经111°30′-113°09′，北纬37°27′-38°25′.气候属于夏季炎热多雨，冬季寒冷干燥，四季气候分明，而且昼夜温差较大.根据国家标准GB 50178-1993《建筑气候区划标准》[11]，太原市是典型的寒冷气候区城市，月平均最高气温24.1 ℃，最低气温-4.6 ℃.冬季采用集中供暖，供暖系统为上供下回单管式，供暖季从每年11月1日到次年3月底.本次调研是在冬季供暖后，2019年12月份的6次上课过程中进行，时间为10：00-12：00，或14：00-16：00；测试期间气象条件包括晴天、阴天.地点选取太原市某大学教学楼二层的一间教室.该教学楼建筑于2012年建成，共4层，教室建筑层高为4.5 m，墙体为混凝土墙(带有聚苯乙烯保温材料)，墙厚度为40 mm，传热系数为0.46 W·(m2·K)-1，窗户为中空玻璃，空气层厚度为12 mm，传热系数为2.86 W·(m2·K)-1.教室平面尺寸为10 m×7.7 m，窗户平面尺寸为2 m×2 m.

1.2 研究方法

1.2.1 环境参数测试方法 热环境参数的测试主要包括室内与室外的参数采集，测试仪器参数如表1所示.室内所测参数包括室内空气温度、湿度、室内风速，以及室内黑球温度；室外参数包括室外温度、湿度.依据国际标准ISO 7726-1998《热环境的人类工效学 物理量测量仪器》[12]要求，室内测试仪器放置于在教室的前、中、后不同点，以及离地板0.1，0.6和1.1 m的3个不同高度水平，各位置点所测量的参数取3个不同高度测量的平均值.

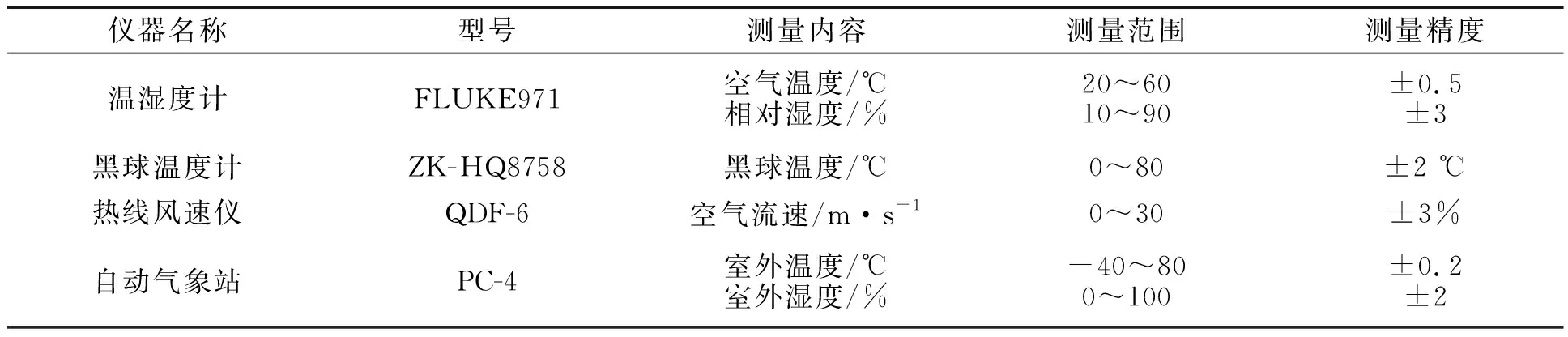
表1 测试仪器参数Tab.1 Test instrument parameters

测量仪器在教室中的具体布置，如图1所示.上课的时间为110 min，其中课间休息10 min，调研者在上课期间每隔10 min记录一次室内热环境参数.对于室外环境参数的测量，可通过室外自动气象站进行记录.为了保证实测数据的准确性，先于课程开始前20 min布置测试仪器，待测试稳定后进行读取数据.本次实验所用仪器精度与测试范围均符合国际标准ISO 7726-1998《热环境的人类工效学 物理量测量仪器》[12]标准规定.

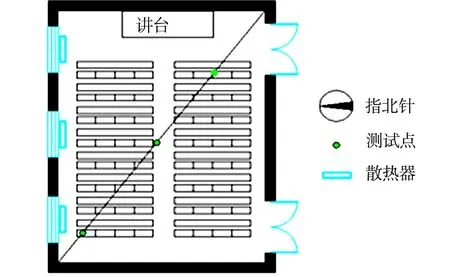
图1 测量仪器布置图Fig.1 Layout of measuring instrument

1.2.2 主观问卷调查 本次实验采取纸质版问卷表，现场主观问卷调查采用纵向研究法[13]，即对受试者在整个调研期间进行重复调查，共6次.由于本次调研是在本科大三学生上课过程中进行的，这两个班的受试学生都是来自于建筑环境与能源应用工程专业，他们已经学习过热环境和热舒适的知识.据前述研究证明，他们充分了解本类调查结果的用途，可以提高热舒适性数据的准确性.调查问卷的内容参照ASHRAE 55标准制定[1]，一部分为具体内容，包括受试者的基本信息，如性别、年龄、衣着等；另一部分为个人对所处热环境的主观评价，如受试者的热感觉、热舒适、热期望、热可接受度等.具体的热舒适投票标尺：

1) 热感觉投票标尺-3，-2，-1，0，1，2，3分别表示冷、凉、稍凉、中性、稍暖、暖、热；

2) 热期望投票标尺-1，0，1分别表示降低、不变、升高；

3) 热舒适投票标尺0，1，2，3分别表示舒适、稍不舒适、不舒适、难以忍受；

4) 热可接受度投票标尺0，1分别表示可接受、不可接受.

2 测试结果与分析

2.1 受试者情况

表2为受试者的基本信息.由表2可知：所有受试者都身体健康，没有服用任何药物；受试者来自中国不同的省份，平均在太原地区已生活2 a以上，可以认为已充分适应太原市的气候环境；受试者平均年龄20.2岁，全为青壮年.

表2 受试者的基本信息Tab.2 Basic information of subjects

为保证测量数据的真实有效性，通常在课堂上同时进行实验环境的测量和问卷调查的填写.参与问卷调查共49人，其中男生30人(占61.2%)，女生19人(占38.8%)，人员数量基本可以满足样本量的要求.最终得到有效问卷294份，其中男性180份，女性114份.受试者的服装热阻、新陈代谢率按ASHRAE 55-2004标准进行计算，可以得到学生受试者的平均新陈代谢率为1.2 MET(1 MET定义为每公斤体质量每分钟消耗3.5 mL氧气).

2.2 室内外热环境参数

测试期间，室内外的温湿度实时变化趋势，分别如图2所示.图2中：θo，θi分别为室外和室内温度；RHo，RHi分别为室外和室内湿度；t为测试时间.

(a) 室外温度 (b) 室外湿度

表3 室内外环境参数Tab.3 Indoor and outdoor environmental parameters

由表3可知：冬季教室室外空气温度的变化范围为-1.9～18.7 ℃，室内空气温度的变化范围为19.7～25.8 ℃；冬季室外相对湿度变化范围为20.6%～60.5%，室内相对湿度变化范围为21.6%～45.8%；室内平均辐射温度的平均值为22.49 ℃；室内温度最大值为25.8 ℃，比国家标准GB 50736-2012《民用建筑供暖通风与空气调节设计规范》中的冬季供暖设计温度(18～24 ℃)最大值要高1.8 ℃，但整体平均温度22.84 ℃在规定的范围内.这表明教室内温度整体是达标的，偶尔存在室内温度过高.

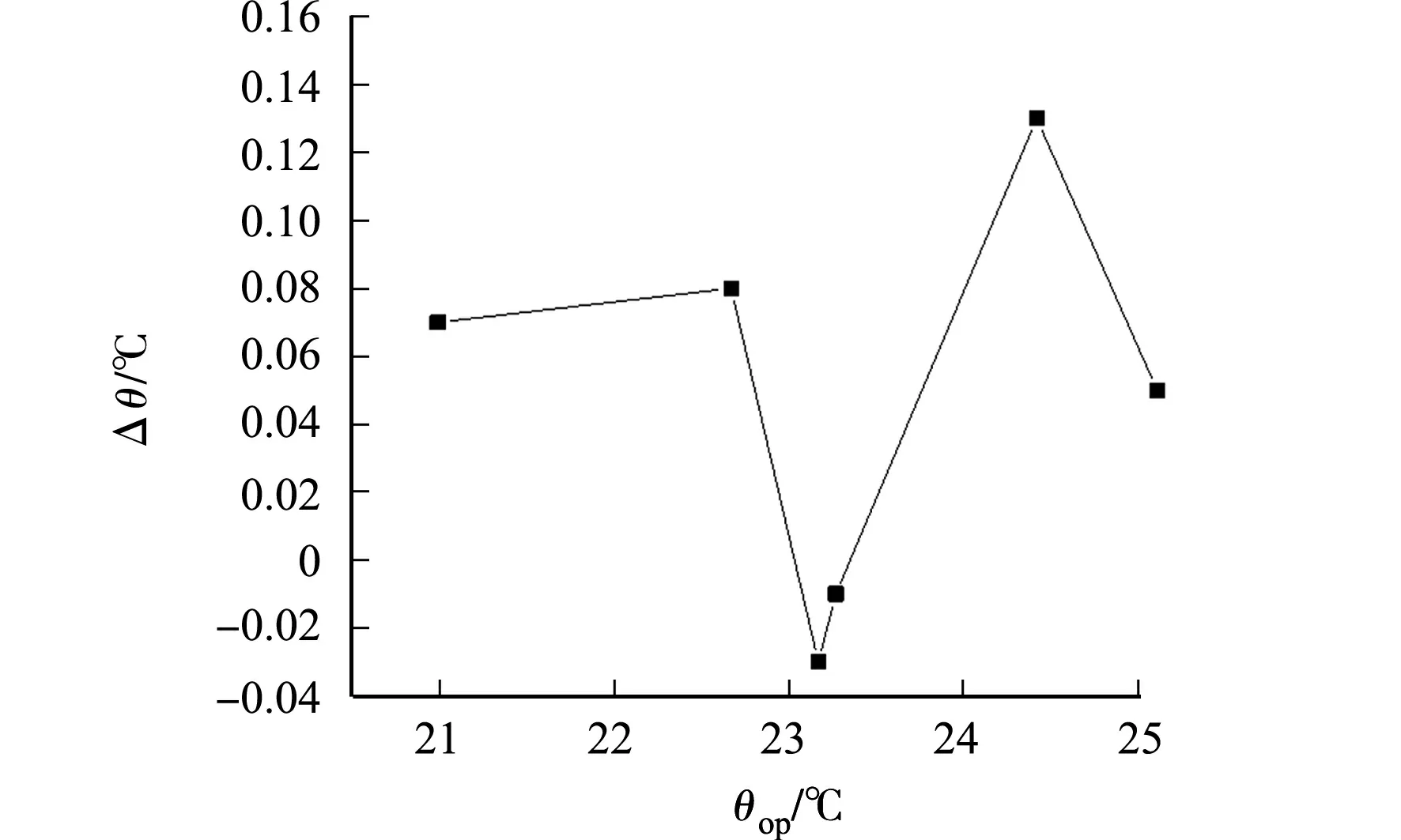
图3 头顶水平和脚踝水平之间的垂直空气温差Fig.3 Vertical air temperature difference between head level and ankle level

由表3还可知：室内平均风速为0.01 m·s-1，这是由于冬季在上课的过程中教室的门、窗是关闭的，所以在整个测试期间风速是比较低的，受试的学生基本没有明显的吹风感.此外，这也符合国家标准GB 50736-2012《民用建筑供暖通风与空气调节设计规范》[14]规定的在供热工况室内风速应小于0.2 m·s-1的范围.根据国际标准ISO 7726-1998《热环境的人类工效学 物理量测量仪器》要求，对于从事接近静坐条件(新陈代谢率在1.0～1.3 MET之间)，在空气速度小于0.2 m·s-1，且平均辐射温度和平均空气温度相差小于4 ℃时，可以使用室内空气温度和平均辐射温度平均值的近似计算操作温度(θop).通过问卷统计可知，冬季室内学生的平均服装热阻为0.158 m2·K·W-1.

头部水平和脚踝水平之间的垂直空气温差，如图3所示.图3中：Δθ垂直空气温差；θop为操作温度.由图3可知：最大垂直空气温差约为0.13 ℃，不超过ASHRAE 55[1]中允许的3 ℃温差极限.由此说明，垂直温差对室内热环境的影响不是很大.

2.3 热感觉与热舒适

对受试者热感觉和热舒适进行统计，结果如图4所示.图4中：ε为投票百分比.

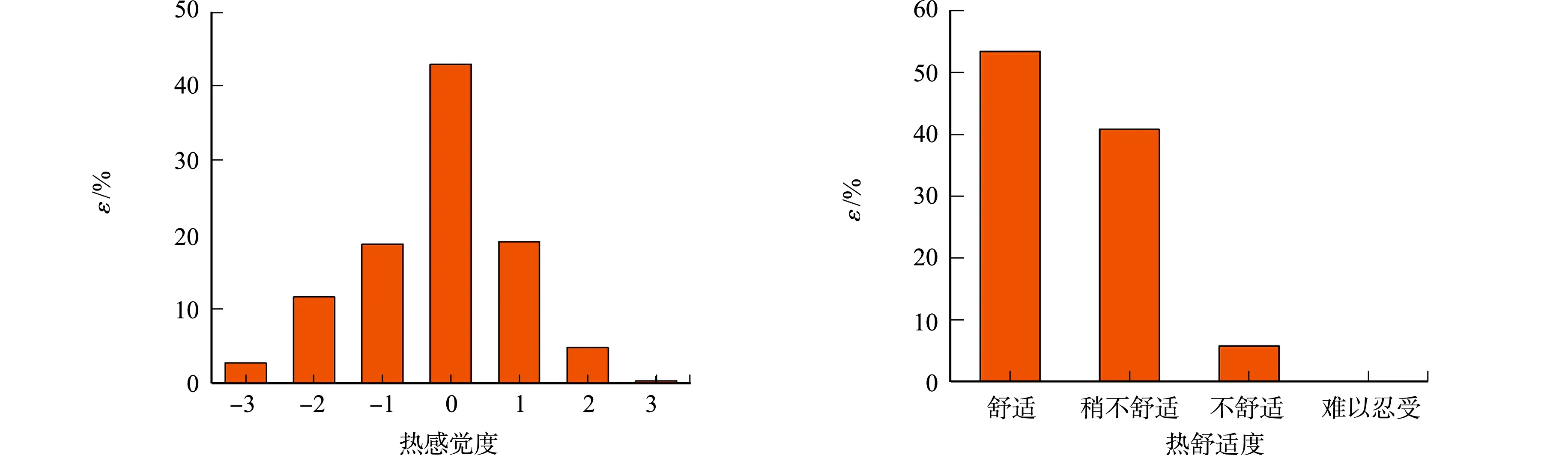
(a) 热感觉 (b) 热舒适图4 热感觉和热舒适的投票频率分布Fig.4 Voting frequency distribution of thermal sensation and thermal comfort

由图4(a)可知:在热感觉投票方面有42.9%的受试者投票为中性，有24.1%的受试者投票为稍暖、暖、热；有33%的受试者投票为稍凉、凉、冷，说明教室在试验期间整体热环境偏冷；投票值在-1～+1之间的频率为80.6%.表明大部分的学生觉得教室内的环境是可以接受的.

由图4(b)可知:有53.4%的学生觉得舒适，有40.8%的学生觉得稍不舒适，而仅有5.8%的学生感到不舒适.表明在测试期间对于大部分学生来说冬季教室内热环境是舒适的，对室内环境满意度较高.同时，投票值为舒适和稍有不适的学生比例率低于整体可接受率(92.5%)，表明受试者对环境的适应能力强，可以在一定程度上忍受不舒适的室内热环境.

图5 热期望投票频率分布Fig.5 Hot expection voting frequency distribution

2.4 热期望

受试者分别对教室内热环境的温度期望、湿度期望、风速期望进行投票，结果如图5所示.由图5可知：1) 在温度期望投票中，希望温度降低的受试者占23.1%，希望温度不变的受试者占49.3%，而有27.6%的受试者希望温度升高.这说明当前教室内的热环境温度适中，能基本满足大部分学生的要求.2)在湿度期望投票中，希望湿度保持不变的受试者占51.4%，希望湿度提高的占43.2%.说明此时教室内空气干燥，相对湿度比较低.3) 在风速期望投票中，有61.6%的受试者期望教室内风速保持不变.说明在冬季学生并不希望通过增加风速来改善热舒适状况，更希望通过增加湿度来改善舒适状况，因为风速增加会增加冷感.

2.5 局部热不舒适

受试者在调研测试期间对典型的身体症状进行投票，包括手、脚、头、背、胳膊、腿等不舒适的症状，其分布比例如图6所示.从图6可知：绝大部分受试的学生感到了局部热不舒适，首先受试者感到脚不舒适的比例为最高约25%，这主要是由于传统的散热器供暖引起的；其次是皮肤、嘴唇和喉咙干燥超过40%，表明调研期间教室内湿度比较低，教室内比较干燥.

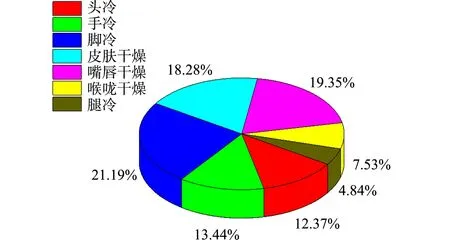
图6 局部不舒适百分比Fig.6 Percentage of local discomfort

3 热舒适模型

3.1 热感觉投票(TSV)模型和PMV模型

参考ASHRAE 7级热感觉投票标尺，对调查测试数据进行统计分析.采用温度频率法，以0.5 ℃为一个间隔进行分组，将操作温度分为若干个区间，以每一个操作温度为自变量，每一个操作温度对应的实测热感觉投票(TSV)为因变量，得到平均热感觉投票与操作温度之间的关系.将现场实测的空气温度、相对湿度、风速、平均辐射温度，以及问卷调查表中记录的受试者新陈代谢率和服装热阻代入GB/T 50785-2012《民用建筑室内热湿环境评价标准》[15]的计算程序，得到对应的预测热感觉投票(PMV)值.同样采用温度频率法，得到PMV值与操作温度之间的回归曲线.将TSV和PMV两条拟合曲线绘制在一张图上，可以更方便地观察实测热感觉与预测热感觉之间的差异，如图7所示.

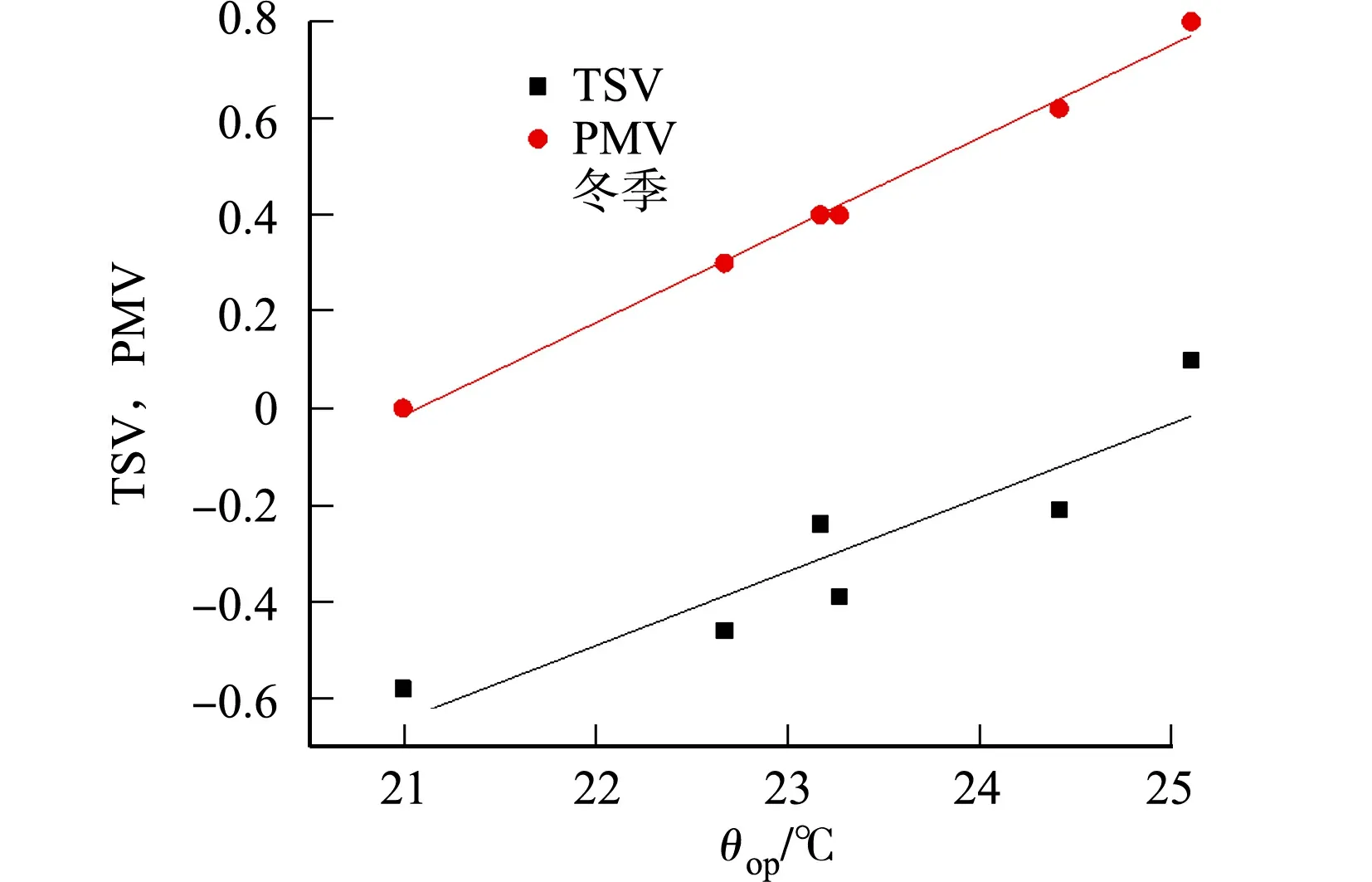
图7 冬季PMV与TSV拟合曲线Fig.7 Fitted curve of PMV and TSV in winter

由图7可知：调研期间TSV和PMV之间存在显著的差异.虽然TSV模型和PMV模型的线性回归曲线在形式上和趋势上基本一致，但二者的曲线并不重合，表明受试学生的实际热感受与PMV指标预测的结果并不相同.PMV曲线在TSV曲线之上，表明在室内温度相同的情况下，受试者的实际热感觉比预测热感觉偏冷.TSV的拟合式斜率均小于PMV的拟合式斜率，表明教室内学生实际热感觉不如PMV模型预测的热感觉好.预测与实测热感觉回归方程为

风险是不确定性对目标的影响，也可理解为损失的不确定性。只要某件事是否发生、是否致损以及致损程度存在多种可能性，这件事就存在风险。从概率学的角度来解释，某件事损失必然发生的概率为1，必然不发生的概率0，如果损失发生的概率区间为(0,1)，则认定该事件存在风险。

PMV=0.190 8top-4.020 3，R2=0.995 0；

TSV=0.152 6top-3.847 2，R2=0.843 1

令PMV=0和TSV=0，就可计算出预测热中性温度为21.07 ℃和实测热中性温度25.21 ℃，二者相差4.14 ℃.在冬季高校教室室内，热中性温度比预测热中性温度高，说明教室内学生对热环境的接受能力要比预测的强.当PMV，TSV等于±0.85时，表示80%受试者对所处热环境表示满意.令PMV，TSV分别等于±0.85，可以求得80%可接受率下的预测热舒适温度范围为16.61～25.53 ℃，80%可接受率下的实测热舒适温度范围为19.64～30.78 ℃.经比较可知，实际可接受温度范围要比预测可接受温度范围宽，表明学生对教室内热环境的接受能力更强.

3.2 Griffiths模型

Griffiths模型与Fanger提出的PMV/PPD((predicted percent dissatisfied))模型是不相同的，PMV/PPD模型可以在稳定的环境中准确的预测中性温度.Griffiths模型是一个即使在任何条件下，投票数很少，温度范围很窄，也能准确预测中性温度[16].其舒适温度计算式为

上式中：θc为舒适温度，℃；θop为操作温度，℃；G为Griffiths常数，℃-1.

对于Griffiths常数，文献[13]发现0.5为最佳的常数.Griffiths常数实质上表示的是在假设没有自适应情况发生的条件下舒适度和温度的关系(斜率).

取G值为0.25，0.33，0.5 ℃-1，计算得到的舒适温度分别21.62，23.06，24.69 ℃，验证了Nicol等的结论.即当Griffiths常数0.5 ℃-1时，得到的热中性温度为24.69 ℃，高于PMV预测的热中性温度21.07 ℃，与TSV计算所得实测热中性温度25.21 ℃相差很小.说明，Griffiths模型可以改变回归系数，准确地预测寒冷地区高校教室的实测中性温度.

3.3 aPMV模型

国内外偏热环境下的诸多现场调查研究结果显示，环境越热，人们的实测热感觉TSV与PMV预测值的偏离就越大，出现“剪刀差”现象.这是由于Fanger教授的PMV/PPD模型没有考虑到人体因受诸如气候、文化、心理、生理、行为等因素的影响.据此，Yao等[9]针对这一差异，将黑箱理论用于人体热调节模型中，第一次引入了适应系数(λ)，将人体适应性行为作为反馈的一部分，提出了预计适应性平均热感觉指标(aPMV)，并建立了aPMV模型.其表达式为

aPMV=PMV/(1+λPMV).

采用温度频率法，计算出每组的TSVi和PMVi，带入上式，可得到λ=-0.05.

综合上述，寒冷地区高校教室内室内热舒适模型应选用适应系数λ来修正，得到修正后的适应性PMV模型为

aPMV=PMV/(1-0.05PMV).

4 严寒地区或寒冷地区的冬季热舒适

寒冷地区或严寒地区不同地点冬季热舒适结果，如表4所示.表4中：Rcl为服装热阻；θM为中性温度.从表4可知：寒冷地区舒适温度都比本次(25.21 ℃)要低，表明其他地区的学生对温度的敏感性要比本次测试的学生对温度的敏感性低.这可能与教室内热环境和各地气候背景有关.因此，寒冷地区高校教室冬季室内设计温度的取值应当结合当地气候条件，考虑服装习惯、心理预期、生理反应等的因素.需要根据室外气候提出合适的热舒适标准.

表4 严寒地区或寒冷地区的冬季热舒适结果Tab.4 Results of winter thermal comfort in severe cold regions or cold regions

5 结论

通过对寒冷地区高校教室室内热舒适的研究，可以得出以下3点主要结论.

1) 冬季高校教室内实测热中性温度25.21 ℃，80%满意度热舒适范围为19.64～30.78 ℃；预测热中性温度为21.07 ℃，80%满意度热舒适温度范围为16.61～25.53 ℃，两者相差4.14 ℃，且实测温度的可接受范围明显比预测的要宽.这表明实测TSV模型与预测PMV模型结果有差别，学生对教室内热环境的接受能力更强.

2) 通过Griffiths模型可以准确地预测出寒冷地区高校教室室内热舒适温度为24.69 ℃，与实测温度比较接近.

3) 对寒冷地区冬季高校教室内热舒适度模型进行修正，引入热适应系数λ为-0.05，得到适用于寒冷地区高校教室热感觉评价的模型为aPMV=PMV/(1-0.05PMV).