采用EEMD-KPCA处理的IHHO-LSSVM滚动轴承寿命预测模型

胡启国， 何奇， 曹历杰

(1. 重庆交通大学 机电与车辆工程学院， 重庆 400074；2. 川庆钻探工程公司 安全环保质量监督检测研究院， 四川 广汉 618300)

滚动轴承作为机械设备的典型零部件，是决定机械标准件故障预测和健康管理的关键部件之一，剩余寿命对于衡量轴承故障信息有着重要价值[1].随着机器学习的发展，基于数据驱动的轴承剩余寿命预测逐渐成为国内外研究的主流.但轴承原始信号中不可避免地会有大量噪声，影响了轴承寿命预测的精确度，因此，需要对原始信号进行降噪处理.为了进行退化特征的提取和寿命预测，Yan等[2]提出一种使用支持向量机和混合退化跟踪模型，预测轴承的剩余使用寿命；Liu等[3]提出一种磷虾群算法，优化基于混合核函数-支持向量回归(HKF-SVR)对轴承性能退化趋势的预测；葛阳等[4]基于t-分布领域嵌入算法(t-SNE)和长短期记忆(LSTM)神经网络，对滚动轴承的剩余寿命进行研究；Jiang等[5]提出一种基于时间序列的多通道卷积神经网络的轴承剩余使用寿命模型.上述方法为轴承退化特征的提取和寿命预测提供了有效借鉴，但仍有考虑不周的地方，如对原始信号噪声没有进行有效处理，寿命预测只能预测短期的退化趋势且预测结果较为保守.Lu等[6]提出最小二乘支持向量机(LSSVM)模型，该模型具有在预测寿命过程中预测精度高和在非线性样本数据中泛化能力好的优点，其预测精度主要受正规化参数C和核参数δ取值不同的影响.

针对以上问题，本文以提高轴承寿命预测精度为目标，提出一种新的寿命预测方法.首先，用集合经验模态分解(EEMD)方法对原始振动信号进行去噪，再根据相关性系数和峭度值对固有模态函数(IMF)分量信号进行筛选并重构数据；然后，提取重构数据中的时域、频域、小波包能量谱等22个特征指标作为特征指标集，并对其进行核主成分分析，选取累计贡献率达到要求的核主成分作为性能退化特征，建立改进的哈里斯鹰优化-最小二乘支持向量机(IHHO-LSSVM)模型.

1 集合经验模态分解原理

Wu等[7]针对经验模态分解(EMD)在使用过程中存在噪声或脉冲产生模态混叠的现象，提出一种EEMD算法，有效地抑制了EMD产生的模态混叠现象.EEMD具体分解过程如下.

1) 在信号中加入一定幅值的白噪声序列，得到新的信号x(t).

2) 新信号x(t)经过EEMD分解，获得h个IMF分量cj(t)和1个余量r(t)，即

(1)

3) 将分解得到的各个IMF分量和剩余余量的均值作为最后结果，最大限度地消除上、下包络线拟合误差.每个IMF分量具有稳态性能和相互独立的特点.分解后的IMF表示为

(2)

2 轴承寿命预测模型的建立

2.1 最小二乘支持向量机预测模型

最小二乘支持向量机由改进支持向量机(SVM)演化而来，其原理是用等式约束替换SVM中的不等式约束，将不等式约束的二次规划问题转化成线性矩阵求解问题，与标准的SVM相比，LSSVM的求解速度更快，精度更高.LSSVM的函数估计问题为

(3)

s.t.yi-ωΦ(xj)-b=0.

(4)

式(3)，(4)中：ω为权向量；e为单位矩阵；ei为松弛变量，表示第i个数据的预测输出和实际输出的误差值；γ为惩罚参数；Φ=[φ(x1)+φ(x2)，…，φ(xn)]T；b为偏差向量.

式(3)和式(4)对应的拉格朗日函数为

(5)

式(5)中：α=[α1，α2，…，αn]T；αi为Lagrange乘子.依据卡鲁什-库恩-塔克(KKT)条件进行求解，对式(5)中的ω，b，e，αi求偏导数，并令其偏导数为零.消掉变量ω，e，最终得到的方程组为

(6)

式(6)中:I=[1，1，…，1]T；y=[y1，y2，…，yn]T.

根据Mercer条件，选择径向基核函数(RBF)作为核函数，其公式为

(7)

式(7)中:σ为核函数宽密度.

最终得到的LSSVM预测回归模型为

(8)

2.2 改进的哈里斯鹰优化(IHHO)算法

哈里斯鹰优化(HHO)算法[8]是Heidari受栗翅鹰捕食猎物过程中的群体合作和追逐方式启发，提出的一种群智能优化算法，可根据场景的动态性和猎物的逃跑模式揭示多种追逐模式，由搜索阶段、转化阶段、开发阶段组成.但原算法易陷入局部最优值，因此，对搜索阶段和能量调控机制进行改进.

改进的搜索阶段中，哈里斯鹰栖息在[lb，ub]的空间某位置观察猎物，迭代时根据所在位置更新概率p.当p<0.5时，其他个体捕食猎物被认为是模仿哈里斯鹰曲折运动的，采用Levy函数(LF)飞行模拟；当p≥0.5时，哈里斯鹰个体移动在内部是随机的，因此，通过哈里斯鹰与其他3只个体初始值的平均位置来更新位置[9]，即

(9)

式(9)中：Xj(t)，Xk(t)，Xl(t)为哈里斯鹰随机初始选择的位置；X0(t)为猎物位置；X(t+1)，X(t)分别为第t+1，t次迭代时个体的位置；Xm(t)为第t次迭代时N只个体的平均位置；D为问题维度.

HHO算法根据猎物的逃逸能量E在搜索和不同的开发行为之间转换，但E的变换是单周期性递减的，无法描述多个轮次共同追捕猎物的情况[10].因此，提出一种调控能量周期性的机制，即多个轮次数以猎物逃逸能量E的递变周期数表示，实现“全局+局部”的寻优搜索能力.以余弦函数刻画E的周期递变性，其定义式为

(10)

式(10)中：E0为猎物的初始能量，E0∈[-1，1]；T为最大迭代数；kp为猎物能量的周期递减数，kp=0，1，2，….当|E|≥1时，HHO进入全局搜索阶段；当|E|<1时，HHO算法进入局部开发过程.

在HHO算法中，通过因子β∈[0，1]描述猎物是否成功逃脱，当β<0.5时，表示猎物逃脱成功，反之则失效.在开发阶段的寻优过程中包含了4种情形[11].

1) 软围攻.当β≥0.5且0.5≤|E|≤1.0时，猎物的能量E充足并逃脱，但最终被捕获，位置更新为

X(t+1)=ΔX0(t)-E|JpX0(t)-X0(t)|.

(11)

式(11)中：ΔX0(t)为第t次迭代时鹰与猎物的位置偏差；Jp为猎物逃跑时的随机跳跃能力，Jp=2(1-r5)，r5是(0，1)上的一个随机数.

2) 硬围攻.当β≥0.5且|E|<0.5时，猎物因能量E较低而被鹰直接捕获，位置更新为

X(t+1)=X0(t)-|EΔX0(t)|.

(12)

3) 渐进式快速俯冲围捕.当β<0.5且0.5<|E|<1.0时，鹰以最优方向俯冲软围捕猎物，位置为

(13)

式(13)中：S是D维随机向量.

4) 渐进式快速俯冲硬捕.当β<0.5且|E|<0.5时，猎物能量较低，鹰俯冲硬捕猎物，位置更新为

(14)

2.3 IHHO-LSSVM模型流程图

选取轴承退化特征作为输入向量，以预测寿命均方误差(MSE)最小化为IHHO寻优目标.以核参数δ和正规化参数C为优化参数的IHHO-LSSVM模型流程图，如图1所示.

图1 IHHO-LSSVM模型流程图Fig.1 Flow chart of IHHO-LSSVM model

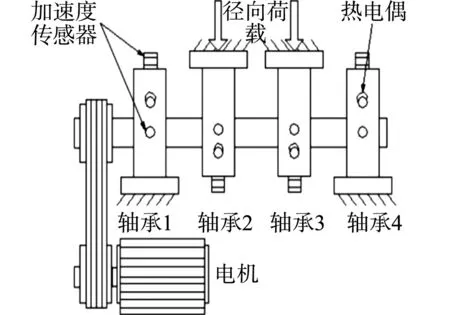
图2 轴承实验台Fig.2 Bearing test bench

3 基于轴承全寿命预测的验证

3.1 实验装置

采用Gousseau等[12]得到的滚动轴承全寿命周期加速轴承性能退化数据.轴承实验台，如图2所示.实验过程中，每个轴承承受26 670 N的径向载荷，每个轴承的横向和纵向各安装了一个压电式加速度传感器，采样间隔为10 min，共采集984个样本，采样频率为20 kHz，共采集20 152 320个数据.轴承运行了一周，直到轴承退化失效.原始信号图，如图3所示.图3中：a为加速度；N为数据样本数量；f为频率.

(a) 原始时域图 (b) 原始频谱图图3 原始信号图Fig.3 Original signal diagram

3.2 基于EEMD的轴承信号降噪

采集的原始信号中一般含有噪声，因此，需要对原始数据进行降噪处理.分解得到21个IMF分量，其相关系数和峭度值，如表1所示.各个IMF分量，如图4所示.

表1 各个IMF的相关系数和峭度值Tab.1 Correlation coefficient and kurtosis value of each IMF

由图4可知：IMF1～IMF12的振动冲击信号较多，而IMF13～IMF20缺少故障的退化信息，因此，对前12个IMF分量进行筛选.分解结果中，IMF分量容易产生虚假的分量，故引入相关系数和峭度值以辨别和剔除虚假分量.根据相关系数和峭度值的计算结果可知：相关系数越接近1，表明该IMF与原始信息关联越紧密，对应的距离越小；峭度值偏离越大，说明包含的轴承故障信息越多[13].因此，根据表1选取IMF1，IMF3～IMF9作为重构信号分量.

(a) IMF1 (b) IMF2 (c) IMF3 (d) IMF4

3.3 验证结果与分析

由于时域、频域各个特征的敏感度皆不相同，筛选对故障敏感度较高的特征，剔除退化趋势不明显的特征.在时域退化特征中，剔除脉冲指标、裕度指标、歪度等几乎无任何变化的退化特征，筛选出8个时域特征，如图5所示.在13个单一频域特征中，选取能够很好地呈现轴承全寿命退化过程的6个频域特征指标，如图6所示.图6中：P1为频域幅值均值；P2为频域标准差；P4为频域主频带位置；P5，P7，P13为频谱分散或集中程度.

(a) 均方根 (b) 标准差 (c) 最大值

由图5可知：8个时域特征均能反映轴承性能的退化趋势，但其敏感程度各有不同；均方根、标准差和绝对平均值在第500个数据点后呈现良好的上升趋势；而峰值、方差、最大值则在第600个数据点后逐渐上升.因此，单一的时域特征可能存在评估能力不足的问题.

(a) P1 (b) P2 (c) P4

由图6可知：P1在第500个数据点之后出现了小幅度的变化，随着故障程度的加深，其特征指标值也不断变大；P2，P4，P5，P7，P13也都反映了轴承退化的趋势.

小波包分解克服了小波分解的不足，提高了信号高频带的频率分辨率和低频带的时间分辨率[14]，其原理是将原始信号分解到不同频带，生成频带能量谱.选用db3小波基函数对重构信号进行3层的小波包分解，得到8个能够反映轴承全寿命的小波包能量谱(S3，1～S3，8)，如图7所示.S3，i中的3表示分解层数，i表示8个频段位置，i=1，2，…，8.

(a) S3，1 (b) S3，2 (c) S3，3 (d) S3，4

由图7可知：8个小波包能量谱能有效增强故障和退化特征，完整保留信号频率信息.在非线性信号中，相比时域、频域的单一特征，小波包能量谱具有分辨率高、精度细化高的优点.小波包能量谱与时域、频域共同构成多维特征集，更能反映轴承全寿命过程的运行状况.共选取22个退化特征，利用核主成分分析(KPCA)将特征退化指标加权融合.将KPCA第一主成分标准化处理，结果如图8所示.

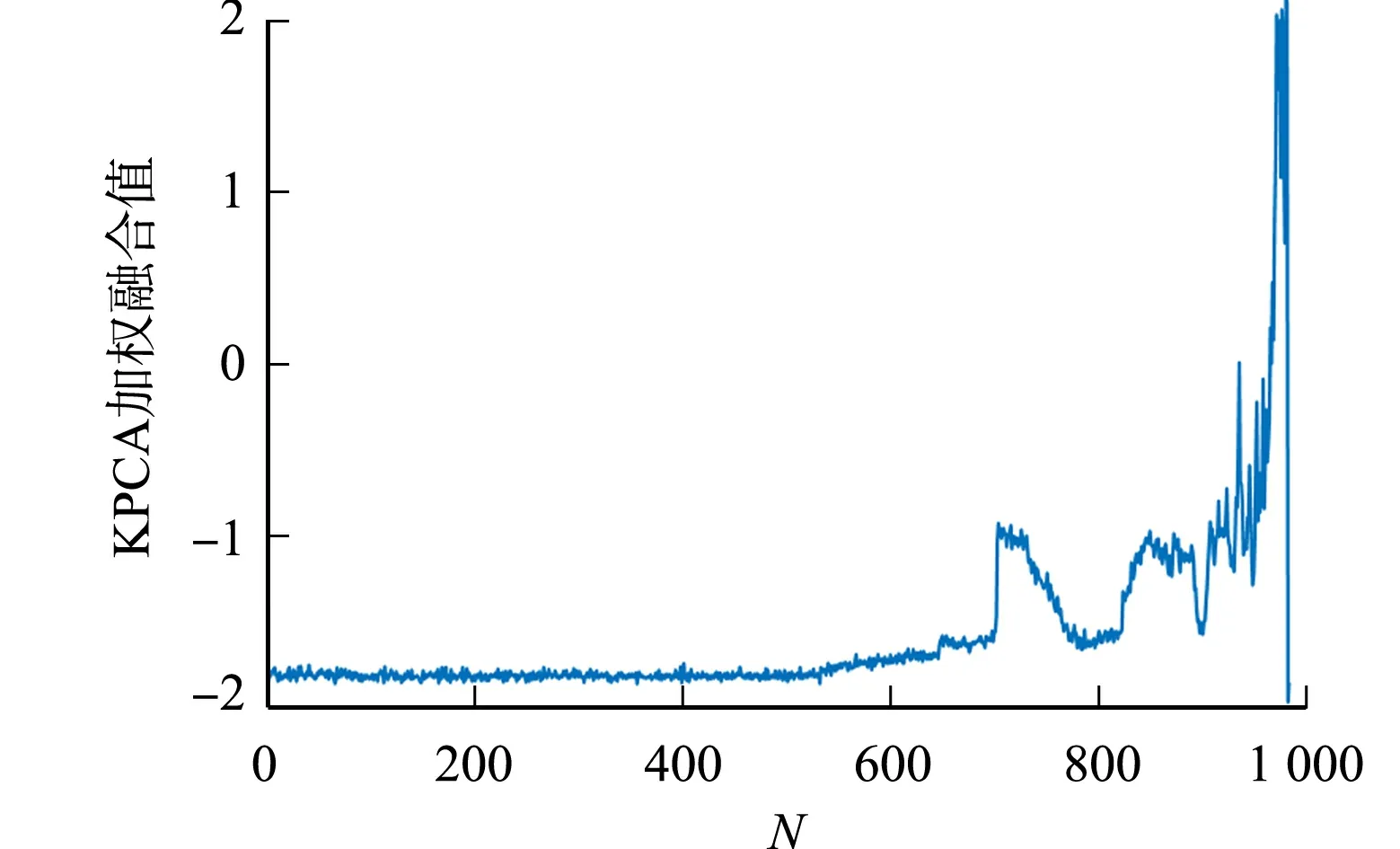
图8 KPCA第一主成分趋势图Fig.8 First principal component trend chart of KPCA

由图8可知：KPCA第一主成分在第500个数据点(早期故障)后开始呈现优良的上升趋势.单一的退化特征则不具备这一优势，利用KPCA加权融合提取主成分呈现出的轴承退化性能趋势比单一的特征更全面，该方法使维数得到约简，计算复杂程度减小.将KPCA各主成分的贡献率从大到小依次排列，各主成分的贡献率，如表2所示.

表2 各主成分的贡献率Tab.2 Contribution rate of each principal component

选取累计贡献率达到85%的前几个主成分[15].由表2可知：前3个主成分的贡献率相加得到的累计贡献率为86.64%，已超过85%.故选取轴承退化期的前3个主成分和对应的剩余寿命序列组成训练样本，建立IHHO-LSSVM寿命预测模型.将第500～703个数据点的退化特征和每一个样本对应的剩余寿命时间序列作为训练样本，等间隔选取第704～984个数据点间的7个样本作为预测样本，代入剩余寿命预测模型[16]中，将LSSVM的核参数δ和正规化参数C通过改进的哈里斯鹰算法进行寻优.对比HHO算法与IHHO算法的适应度(适应度值选择均方误差)曲线，如图9所示.图9中：n为迭代次数.由图9可知：IHHO算法的收敛精度比HHO算法提高了许多.

图9 HHO算法与IHHO算法的适应度曲线对比Fig.9 Comparison of fitness curves between HHO algorithm and IHHO algorithm

文中方法是利用EEMD去除噪声，分解、重构信号，再用KPCA融合的前3个主成分作为轴承性能退化指标，最后采用IHHO-LSSVM作为寿命预测模型进行模拟.为了评估轴承寿命的预测效果，将IHHO-LSSVM模型与采用EEMD-KPCA处理的LSSVM模型和IHHO-LSSVM模型的寿命预测结果进行对比，如图10所示.图10中：tr为剩余寿命.由图10可知：3种模型预测的轴承剩余寿命与真实寿命变化趋势一致.

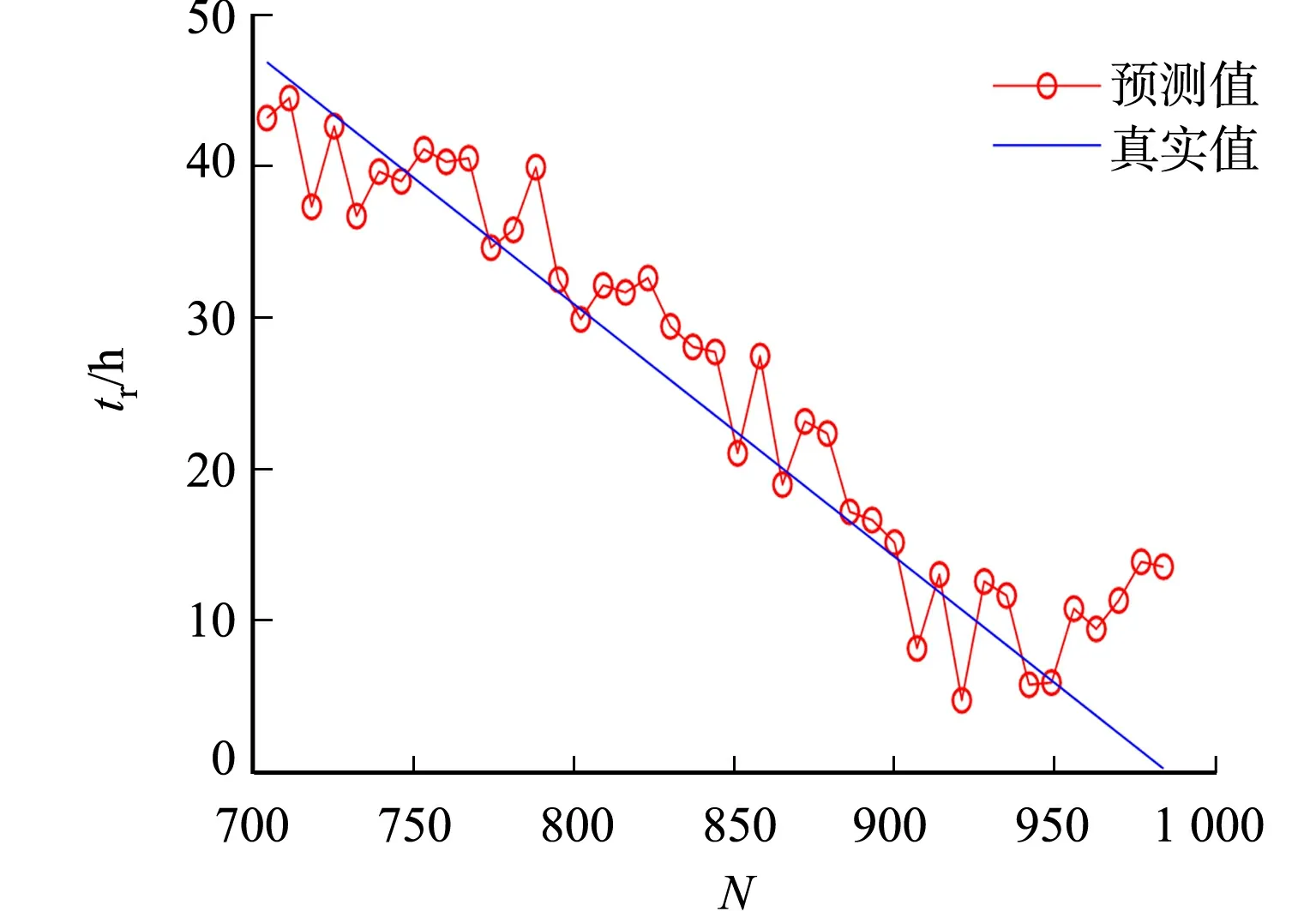
(a) EEMD-KPCA处理的LSSVM模型

3种模型的预测误差对比，如表3所示.对比图10和表3可知：EEMD-KPCA处理的IHHO-LSSVM模型的均方根误差、平均绝对误差和均方误差均小于IHHO-LSSVM模型和EEMD-KPCA处理的LSSVM模型，说明EEMD分解重构具有消除噪声的作用，KPCA消除了时域、频域等各特征指标间相关性导致的冗余数据；IHHO-LSSVM模型的预测准确率相比其他支持向量机模型有所提高.

表3 3种模型的预测误差对比Tab.3 Comparison of prediction errors of three models

4 结论

1) 提出一种新的EEMD-KPCA方法，对轴承进行特征处理与提取，该方法既能去噪、又能采用核主成分分析方法剔除无关特征，提高了数据特征的敏感性，为建立寿命预测模型提供了良好的基础.

2) 提出一种改变搜索阶段和能量调控机制的改进的哈里斯鹰优化算法.与原算法相比，该方法更容易找到LSSVM预测模型的核参数δ和正规化参数C的最优解.

3) 建立一种采用EEMD-KPCA处理的IHHO-LSSVM滚动轴承寿命预测模型，与IHHO-LSSVM预测模型和EEMD-KPCA处理的LSSVM模型相比，所提模型的预测精度得到了提高，为滚动轴承寿命预测提供了一种新的方法.