计及直流分压器传变特性的行波保护定值整定方法

彭贺翔，廖 凯，李 波，李小鹏，何正友

（1. 西南交通大学电气工程学院，四川省成都市 611756；2. 国网四川省电力公司电力科学研究院，四川省成都市 610072）

0 引言

特高压直流输电具有输送容量大、输电距离远、稳定性高等优点，在中国电网建设中得到广泛应用［1-2］。直流线路行波保护作为现有特高压直流系统中输电线路的主保护，其可靠性对整个直流系统的稳定运行起着至关重要的作用［3-4］。直流线路行波保护主要采用电压、电流的高频变化信号进行故障诊断［5-6］，且其各判据中故障特征量的生成均基于直流分压器的测量值。然而直流分压器除本体外，还包括由二次分压板、电子隔离装置等组成的二次系统［7-8］，受其二次系统的影响，直流分压器难以准确地传递一次侧各频段信号，尤其是高频电压信号。根据对某直流工程备用直流分压器二次系统的测试，直流分压器二次系统的幅频特性在高频时有放大效应，其宽频传递特性并不理想。在后续某次对直流分压器的年度检修中，发现部分二次分压模块的零位电压过大，线性度和一致性较差，影响了直流分压器的整体传变特性。因此，如果在对行波保护进行定值整定时未考虑直流分压器传变特性对行波保护性能的影响，势必造成行波保护定值选取不合理，导致保护可靠性降低。

目前，由于特高压直流输电系统故障特性复杂，其保护定值整定方法中所用到的电压、电流故障边界值难以通过解析法求得。因此，直流输电系统保护定值主要依靠仿真结果来确定［9-10］。然而，目前直流输电系统保护定值整定的流程不清晰，且整定过程中考虑因素不全面，实际工程中由于定值设置不合理造成保护误动的情况仍然时有发生［11-12］。针对这一问题，文献［13-14］梳理了现有高压直流输电保护的特点，针对不同保护的特点提出了基于故障特征量的整定流程。文献［15-16］针对2 种特高压直流线路保护，分析了过渡电阻、故障位置等因素对保护定值整定的影响，分别提出了针对2 种特高压直流线路保护的整定流程。然而，上述研究在进行定值整定时忽略了直流分压器传变特性对保护性能的影响，未将直流分压器传变特性作为影响保护定值整定的因素纳入整定流程中，势必造成保护定值选取不合理，进而影响保护性能。

目前关于直流分压器传变特性及其对直流输电保护系统性能影响的研究较少，这也是直流分压器传变特性未被纳入保护定值整定的原因之一。文献［17］分析了直流分压器二次系统对直流分压器频率响应的影响，讨论了直流分压器用于直流谐波测量的可行性。文献［18］分析了直流分压器二次侧放电回路击穿后的暂态过程，研究了直流分压器暂态特性引发特高压直流误闭锁的机理。在此基础上，文献［19］提出采用放电管串联压敏电阻方案作为换流站直流分压器的二次侧保护，以避免因保护误动作造成的双极闭锁事故。然而，上述文献均未针对直流分压器传变特性对直流保护系统的影响展开具体分析。

本文针对目前直流线路行波保护定值整定流程不清晰、考虑因素不全面等问题，提出一种计及直流分压器传变特性的行波保护定值整定方法。从直流分压器的传变特性入手，构建基于实际工程参数的直流分压器等效电路模型，推导直流分压器传递函数。基于2 类直流分压器频率响应特性及阶跃响应特性，研究2 类直流分压器传变特性对行波保护性能的具体影响，并将直流分压器传变特性作为影响保护定值整定的因素纳入整定流程。最后，基于PSACD/EMTDC 搭建仿真模型，验证所提定值整定方法的有效性与可靠性。

1 直流分压器结构及其传变特性

针对2 种不同结构的直流分压器，首先，介绍其拓扑结构并建立等效电路模型；其次，推导两种不同结构直流分压器的传递函数；最后，基于所推导出的传递函数，分析两种不同结构的直流分压器的频率响应特性及阶跃响应特性。

1.1 直流分压器结构

直流分压器结构如图1 所示，其由直流分压器本体、平衡单元、二次分压板和电子隔离装置4 个部分组成。800 kV 的直流线路电压在通过直流分压器本体后被降低至70 V；平衡单元中装设了气体放电管，起到保护二次系统的作用；后续模块中，二次分压板将该70 V 电压进一步降低至5 V；该5 V 电压信号在通过电子隔离装置后，送达特高压直流保护系统。

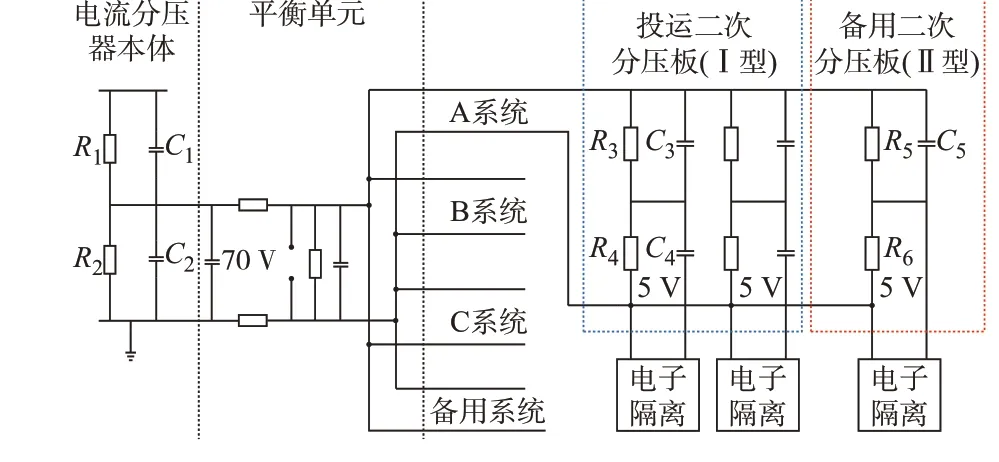
图1 直流分压器结构Fig.1 Structure of DC voltage divider

1.2 直流分压器传递函数

由于平衡单元在直流分压器中只起保护作用，而对直流分压器整体传变特性无影响，因此在本节中仅对直流分压器本体、二次分压板及电子隔离装置的传递函数进行推导。

1.2.1 直流分压器本体传递函数推导

直流分压器本体采用阻容结构进行分压，由于杂散电容对直流分压器的传变特性影响并不大［17］，故直流分压器本体可等效为如图1 所示的结构。其阻容参数如附录A 图A1（a）所示，各参数均为特高压直流输电系统中的实际工程参数。直流分压器本体标定变比为80 000∶7。

文献［18］对直流分压器本体传递函数进行了详细推导。直流分压器本体传递函数H1（s）为：

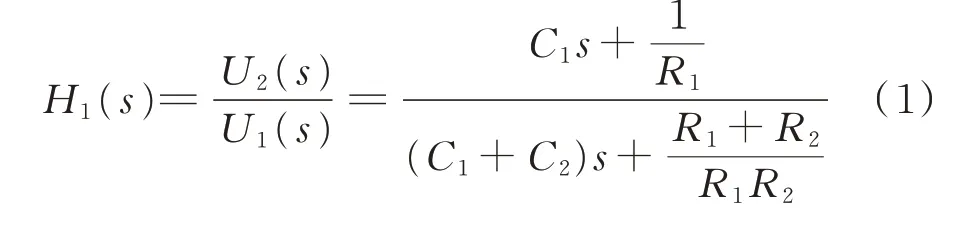
式中：R1和R2分别为直流分压器本体高、低压桥臂等效电阻；C1和C2分别为直流分压器本体高、低压桥臂等效电容；U1和U2分别为输电线路电压和直流分压器本体二次侧电压。

当直流分压器本体参数满足R2C2=R1C1时，其变比为一个与频率无关的定值，此时直流分压器本体在各频段下均能按该定值传变信号。

1.2.2 二次分压板传递函数

二次分压板采用阻容结构进行分压，且存在2 种拓扑结构：Ⅰ型和Ⅱ型。Ⅰ型二次分压板拓扑与直流分压器本体相同，而Ⅱ型二次分压板则没有低压桥臂上的电容。2 种二次分压板的阻容参数如附录A 图A1（b）、（c）所示，各参数均为特高压直流输电系统中的实际工程参数。二次分压板标定变比均为70∶5。

由于Ⅰ型二次分压板的拓扑结构与直流分压器本体相同。因此，本文不再对Ⅰ型二次分压板传递函数进行推导，直接给出其传递函数H2（s）为：

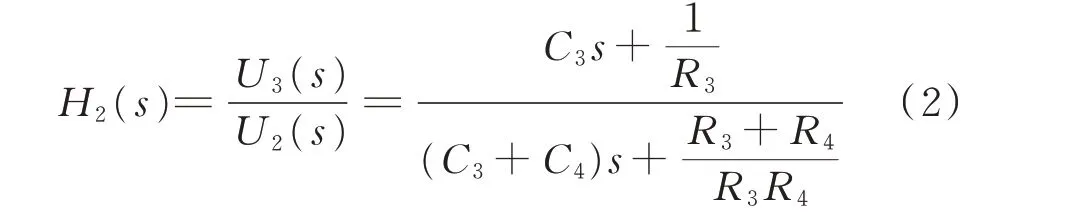
式中：R3和R4分别为Ⅰ型二次分压板高、低压桥臂等效电阻；C3和C4分别为Ⅰ型二次分压板高、低压桥臂等效电容；U3为Ⅰ型二次分压板的二次侧电压。

对Ⅱ型二次分压板等效电路进行分析，可得其一、二次侧电压间的关系为：

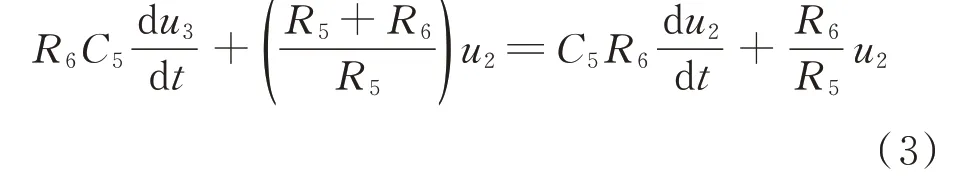
式中：R5和R6分别为Ⅱ型二次分压板高、低压桥臂等效电阻；C5为Ⅱ型二次分压板高压桥臂等效电容；u2和u3分别为输入Ⅱ型二次分压板的电压及Ⅱ型二次分压板的二次侧电压。

对式（3）进行拉普拉斯变换可得Ⅱ型二次分压板传递函数H3（s）为：

由此可见，当输入直流电压信号时，Ⅱ型二次分压板能按标定变比对信号进行传变。随着输入信号的频率上升，Ⅱ型二次分压板的变比逐渐增大到接近于1。

1.2.3 电子隔离装置传递函数

电子隔离装置主要由低通滤波、模数转换、光电耦合、数模转换4 个环节组成，其结构如附录A 图A2 所示。其中，低通滤波环节用来滤除高频噪声，模数转换、光电耦合、数模转换环节用来实现信号的不失真传输。目前特高压直流输电保护系统的采样频率为10 kHz，而模数转换及光电耦合所涉及的相关技术已较为成熟，采样频率通常在几百千赫兹左右，远高于保护系统的采样频率，能保证各个频段下信号的精确转换［20-22］，对电子隔离装置整体的传变特性无影响。因此，电子隔离装置的传递函数可用低通滤波环节的传递函数来表征。

电子隔离装置的低通滤波环节通常采用二阶巴特沃斯滤波器，截止频率通常设置为3 kHz，其传递函数G(s)为：

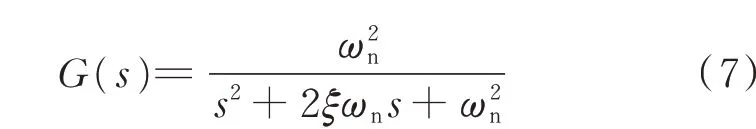
式中：ξ为阻尼系数；ωn为截止频率。

综上所述，在建立电子隔离装置等效电路模型时，可将其等效为一个截止频率为3 kHz 的二阶低通滤波器。

1.3 直流分压器传变特性分析

基于1.2 节分析，将直流分压器各部分传递函数级联后可得到直流分压器整体的传递函数。直流分压器频率响应特性和阶跃响应特性如图2 所示。以下称采用Ⅰ型二次分压板的直流分压器为Ⅰ型分压器，采用Ⅱ型二次分压板的直流分压器为Ⅱ型分压器。

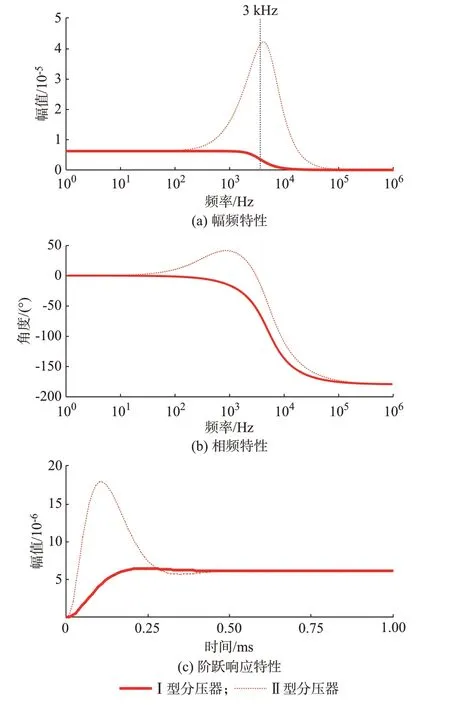
图2 直流分压器传变特性Fig.2 Transfer characteristics of DC voltage divider

1）频率响应特性分析

图2（a）、（b）所示为2 类直流分压器在实际工程参数下的频率响应特性。由图可知，Ⅰ型分压器能准确传变低频信号，但当注入信号频率超过1 kHz后，信号的幅值开始下降，相位开始明显滞后。Ⅱ型分压器也能准确传变低频信号，但当注入信号的频率在0.2～20.0 kHz 内时，信号的幅值将出现放大；当注入信号的频率在0.1～3.0 kHz 内时，信号的相位将发生超前。

2）阶跃响应特性分析

图2（c）所示为2 类直流分压器在实际工程参数下的阶跃响应特性。由图可知，Ⅰ型分压器阶跃响应无超调，上升时间为153 μs；Ⅱ型分压器阶跃响应超调量高达288.12%，但其上升时间仅为26 μs。

由上述分析可见，直流分压器的传变特性并不理想，在频域内无法准确传变各个频段下的信号，而在时域内，对阶跃信号的传变出现超调现象。然而，行波保护判据中故障特征量的生成均基于直流分压器测量值，这将导致直流分压器传变特性势必对行波保护故障特征量的上升时间与幅值产生影响，进而影响保护性能。

2 直流分压器传变特性对行波保护性能的影响

为研究直流分压器传变特性对行波保护性能的影响，本章通过典型区内外故障及扰动的仿真，分析直流分压器传变特性对行波保护故障特征量的影响。结合行波保护判据和逻辑，研究直流分压器传变特性对行波保护输出结果的影响。

2.1 行波保护原理

行波保护基本原理为：首先，通过构造不平衡电压方程，生成极波和地模波；其次，对极波和地模波进行差分计算，生成行波保护的故障特征量；最后，将生成的故障特征量与定值进行比较，构成极波判据和地模波判据；若判据满足行波保护的定值要求，则输出一个比较信号，该信号通过由延时、展宽等环节构成的行波保护逻辑后输出行波保护动作信号。行波保护判据及逻辑详见附录B。

2.2 直流分压器传变特性对行波保护的影响

参照向家坝—上海特高压直流工程参数，利用PSCAD/EMTDC 软件建立±800 kV 双极特高压直流输电系统及其行波保护的仿真模型。系统额定输送容量为6 400 MW，杆塔结构如附录A 图A3 所示，线路模型采用频变参数模型，线路总长度为1 935 km。行波保护相关定值如表1 所示。

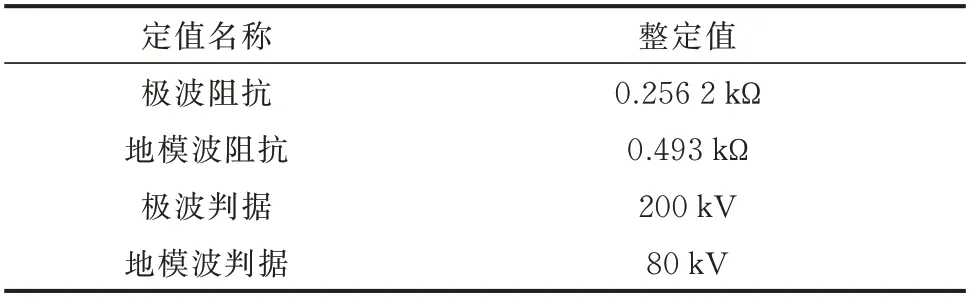
表1 行波保护相关定值Table 1 Related settings of traveling wave protection

本节通过设置典型区内外故障及系统扰动，结合行波保护判据与逻辑，仿真分析直流分压器传变特性对行波保护的影响。由于本文研究重点是直流分压器对特高压直流输电系统保护性能的影响，因此，在进行仿真时不考虑电流互感器传变特性对行波保护性能的影响。

2.2.1 区内故障情况

进行区内故障仿真时，应优先考虑最易造成行波保护拒动的情况。故障位置距离线路首端越远、过渡电阻越大，故障的特征越微弱。因此，仿真设置t=2.35 s 时，极1 线路末端（逆变侧出口处）发生接地短路故障，过渡电阻为100 Ω。以此考察区内故障时，直流分压器传变特性对行波保护性能的影响（仿真针对极1 配置的行波保护响应情况进行故障分析，认为极1 线路为保护区内）。区内故障时直流分压器传变特性对电压及行波保护故障特征量的影响情况如图3 所示。图中：ΔP2为极波差分量；ΔG17为地模波差分量。

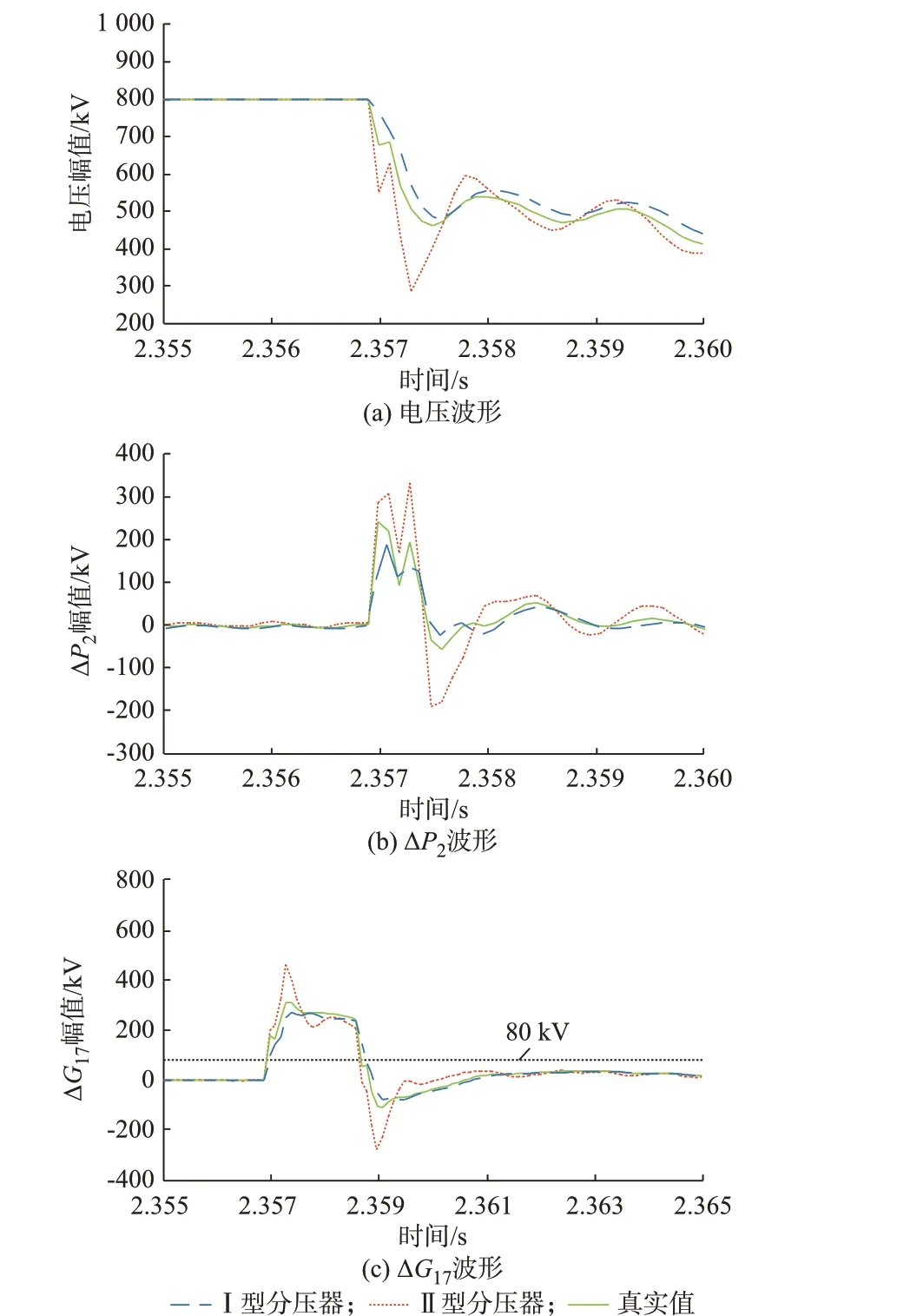
图3 区内故障时直流分压器传变情况Fig.3 Transfer situation of DC voltage divider with internal fault

由图3（a）可知，当系统运行于额定工况时，2 类直流分压器均能正确传变线路电压；而当发生故障时，线路电压经直流分压器传变后会产生畸变，进而影响行波保护中故障特征量的上升时间和幅值。

本文研究了直流分压器传变特性对行波保护中极波差分量ΔPj和ΔG17上升时间和幅值的影响，并结合保护判据与逻辑，分析直流分压器传变特性对行波保护输出结果的影响。由于ΔPj判据的变化规律十分相似，此处只考虑直流分压器传变特性对ΔP2和ΔG17的影响。

由图3（b）可知，未考虑直流分压器传变特性时，ΔP2的幅值为247.4 kV，达到整定值所需时间为0.8 ms；经过Ⅰ型分压器传变后，ΔP2的幅值仅为198.7 kV，已达不到整定值，行波保护拒动；而经过Ⅱ型分压器传变后，ΔP2的幅值为340.4 kV，达到整定值所需时间为0.8 ms，行波保护正确动作。由图3（c）可知，无论是否考虑直流分压器传变特性的影响，ΔG17幅值均远高于整定值，且ΔG17超过整定值的时长均达到防抖动元件设置时长，地模波逻辑在各情况下均能正确输出动作信号。

由上述分析可知，当区内线路末端发生高阻故障时，行波保护各故障特征量经Ⅰ型分压器传变后波形失真不严重，但ΔP2已达不到整定值，造成保护拒动；而各故障特征量经Ⅱ型分压器传变后，虽然波形失真较严重，但保护仍能正确动作。

2.2.2 区外故障情况

进行区外故障仿真时，优先考虑易造成行波保护误动的故障情况。因此，本文设置t=2.35 s 时，极2 线路中点发生金属性接地故障。

极2 故障时极1 整流侧线路电压或行波保护的响应量如附录A 图A4 所示。由图A4 可知，发生区外金属性故障时，无论是否考虑分压器影响，地模波判据均能正确识别故障极，且ΔP2幅值均超过整定值。附录A 图A5 为极波逻辑输出结果。由图A5可知，在不考虑分压器和考虑Ⅰ型分压器的情况下，虽然ΔP2幅值均超过整定值，但是极波逻辑的4 个通道未同时输出动作信号，行波保护不会误动；而考虑Ⅱ型分压器的情况下，行波保护误动。

2.2.3 系统扰动情况

由于噪声干扰、雷击干扰等系统扰动可能造成线路行波出现短时波动，进而造成行波保护误动。因此，本文分析在噪声干扰及雷击干扰的情况下直流分压器传变特性对保护的影响。

1）噪声干扰情况

噪声信号是由系统内部产生的一种信号干扰，原信号混入噪声后会使波形特征发生一定程度的改变，干扰保护判别。噪声干扰仿真条件设定为：故障位置为极1 线路末端；过渡电阻为100 Ω；在量测端电压加入30 dB 的高斯白噪声。

本文进行50 次噪声干扰测试，获取区内末端故障时经直流分压器传变后ΔP2幅值的边界值，仿真结果如附录A 表A1 所示。由表A1 可知，当加入噪声干扰后，若考虑Ⅰ型分压器传变特性的影响，ΔP2的幅值在现有保护定值的上下波动，可能造成保护的拒动。因此，在后续整定过程中定值选取应留有裕度，使得所取定值具有一定的抗噪声能力。

2）雷击干扰情况

试验利用甘肃农业大学草业学院微生物课题组PGPR资源库的优良菌株，选用农业废弃物(花土、马铃薯渣、木炭、泥炭和菌糠)作为微生物接种剂载体，探究不同材料载体研制的的微生物接种剂对苏丹草生长和品质以及土壤养分、土壤3大微生物数量的变化，以期筛选出苏丹草最适微生物接种剂的载体，为禾本科牧草增产、增效提供科学的理论依据。

雷击会造成特高压直流线路电压在短时间内迅速下降，干扰保护判别。雷击干扰仿真条件设定为：雷电采用1.2 μs/50 μs 的双指数模型；雷电电流幅值为31 kA；雷击位置为极1 线路中点。

雷击干扰仿真结果如附录A 图A6 所示。雷电引起的输电线路行波的频率一般为几万赫兹至兆赫兹的数量级，2 类分压器在此频段已经几乎截止。因此，无论是否考虑分压器传变特性的影响，雷击干扰下ΔP2和ΔG17的波形均相同。雷击造成ΔP2和ΔG17的幅值远超整定值，此时地模波判据动作。然而，由于ΔP2超过整定值时间较短，保护仍能够正确判别。

3 计及直流分压器传变特性的行波保护定值整定

由第2 章分析可知，直流分压器传变特性将对行波保护性能造成影响，严重时甚至可能导致保护误动或拒动。因此，在进行保护定值整定时，应充分考虑直流分压器传变特性对保护性能的影响，针对直流系统中所采用的不同直流分压器类型提出相应的保护定值，提高行波保护的可靠性。本文提出的行波保护定值整定流程如图4 所示，具体整定步骤见3.1 节至3.4 节。

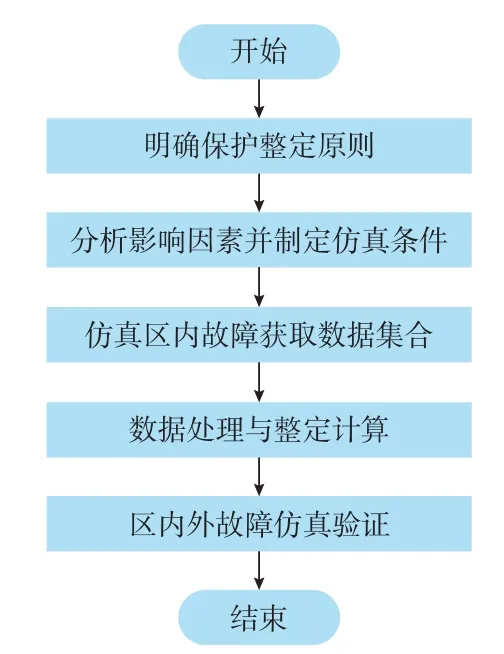
图4 行波保护定值整定流程图Fig.4 Flow chart of traveling wave protection setting

3.1 保护整定原则

在对行波保护进行定值整定之前，应首先明确行波保护中各判据的功能，对于具有不同功能的判据，需采取不同的整定原则。

1）极波判据整定原则：对极波判据进行定值整定的关键在于定值大小的选取，其准确性影响了保护灵敏性、保护区域的大小。在极波判据中，ΔP2为主要判据，用来识别区内故障，而其余3 个极波差分判据作为辅助判据，通过与ΔP2配合躲开系统扰动，与ΔP2取相同定值。因此，在对极波判据进行整定时，应重点关注ΔP2在故障时幅值的大小，以此为依据确定极波定值。

2）地模波判据整定原则：对地模波判据进行整定的关键在于地模波逻辑中防抖动元件时长的选取。当故障发生时，ΔG17幅值往往远超整定值，但只要故障后ΔG17的正负方向与相应极对应，且ΔG17超过整定值的时长达到防抖动元件设置时长，地模波逻辑均能正确输出故障极。因此，在对地模波判据进行定值整定时，应重点关注地模波逻辑中防抖动元件时长的选取。

3.2 影响因素分析及仿真条件制定

特高压直流输电系统存在额定运行与降压运行等不同工况，在不同工况下行波保护会自动切换定值大小。无论在何种工况下，对定值整定造成影响的因素均相同，且进行定值整定时所设定的仿真条件均类似。因此，本文以额定工况为例，进行影响因素分析及仿真条件制定。

1）考虑直流分压器传变特性对定值整定的影响。直流分压器传变特性通过影响行波保护故障特征量的传变，进而影响保护性能。因此，在进行定值整定时不可忽略直流分压器传变特性的影响。本文在制定仿真条件时，以传递函数的形式表征2 类直流分压器的传变特性，线路电压首先经过该传递函数再送入保护系统，以此衡量直流分压器传变特性对行波保护性能的影响，并针对不同类型的直流分压器，提出不同的行波保护定值。

2）考虑过渡电阻对定值整定的影响。过渡电阻越大，行波幅值越小。因此，为使行波保护定值具有一定抗过渡电阻能力，在进行区内故障仿真时重点考虑高阻故障，在进行区外故障仿真时重点考虑金属性接地故障。本文在设置过渡电阻时参考现场联调数据，区内仿真时设置过渡电阻为100 Ω，区外故障时设置金属性接地故障。

3）考虑故障位置对定值整定的影响。为提高所取定值的可靠性，区内故障仿真时考虑线路全长，并重点关注线路末端故障情况。因此，区内故障设置为：线路前90%部分每10%线路长度设置一故障点（F1至F10），线路90%～100%部分每1%线路长度设置一故障点（F11至F20）。

在进行区外故障仿真时，应分别考虑本极区外和对极线路上产生较大扰动的情况。因此区外故障设置为：极1 整流侧与逆变侧交流母线三相接地故障（F21、F22）；极1 整流侧与逆变侧阀厅出口处接地故障（F23、F24）；极2 线路首端、20%、40%、60%、80%和100%处接地故障（F25至F30）。具体故障设置点如附录A 图A7 所示。

3.3 仿真数据集合获取

参照向家坝—上海特高压直流输电工程参数，利用PSCAD/EMTDC 软件建立±800 kV 双极特高压直流输电系统及其行波保护的仿真模型，获取各故障情况下行波保护各判据的数据。

3.4 数据处理与整定计算

在对极波判据进行定值整定时，应重点关注极波微分判据定值的选取，进行数据处理与整定计算时应遵循以下步骤：

1）每次区内仿真获取一个极波差分量幅值ΔP2，max。

2）数次仿真后形成极波差分量幅值数据集合S={ΔP2，max}。

3）取出极波微分量幅值数据集合中最小值smin。

4）smin除以可靠系数得到极波判据整定值Pset。

由于故障发生时，ΔG17幅值往往远超整定值，因此，对地模波定值进行整定时，定值的选取可参考现有定值，并验证地模波逻辑中防抖动元件时长的选取是否合理。进行数据处理与整定计算时应遵循以下步骤：

1）每次区内仿真获取一个地模波判据超过现有整定值的时长TG。

2）数次仿真后形成地模波判据超过现有整定值时长的集合T={TG}。

3）取出地模波判据超过现有整定值时长集合中的最小值Tmin。

4）Tmin与防抖动元件设置时长Tset进行比较。若Tmin＞Tset，则沿用现有时长；若Tmin＜Tset，则用Tmin除以可靠系数得到新防抖动元件设置时长。

通过以上4 个步骤获取行波保护各判据定值后，通过设置典型区内外故障仿真验证所取定值的可靠性。

4 算例验证

参照向家坝—上海特高压直流工程参数建立仿真模型，模型参数在2.2 节已给出。根据第3 章中制定的仿真条件进行区内故障仿真，可得行波保护部分故障特征量仿真结果如附录A 表A2 所示。将ΔP2、ΔG17的幅值的仿真结果进行曲线拟合后可得ΔP2、ΔG17的幅值随故障位置变化的情况，如图5所示。

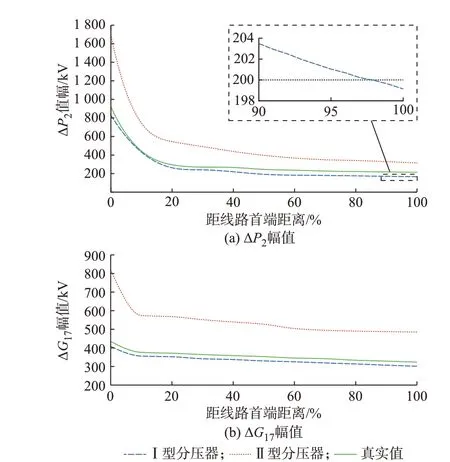
图5 ΔP2及ΔG17幅值随故障位置变化情况Fig.5 Amplitude changing of ΔP2 and ΔG17 with fault location

根据区内故障仿真结果，并遵循第3 章制定的定值整定流程，可得采用Ⅰ、Ⅱ型分压器时极波的定值分别如式（8）、式（9）所示。

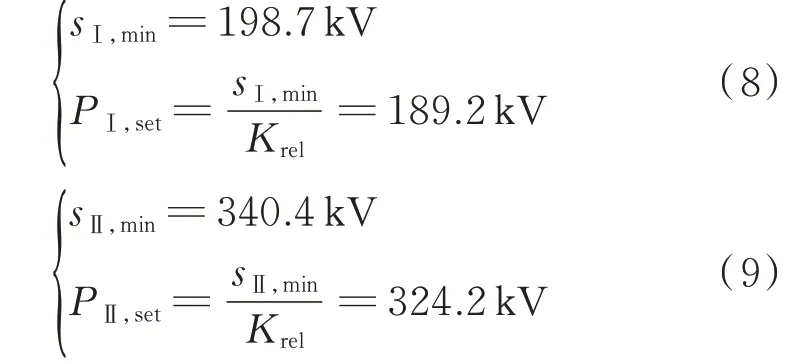
式中：sⅠ，min和sⅡ，min分别为采用Ⅰ、Ⅱ型分压器时极波差分量幅值的最小值；PⅠ，set和PⅡ，set分别为采用Ⅰ、Ⅱ型分压器时极波判据整定值；Krel为可靠性系数，取值范围为1.05～1.20。由于本文考虑了直流分压器传变特性对行波保护性能的影响。因此，在选取可靠性系数Krel时，选取一较小值1.05。

对于地模波判据，ΔG17超过整定值时长的边界值如式（10）所示。

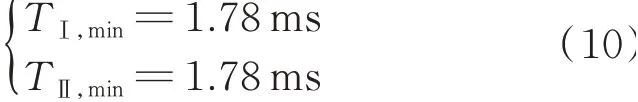
式中：TⅠ，min和TⅡ，min分别为采用Ⅰ、Ⅱ型分压器时ΔG17超过整定值时长的边界值。

由于无论采用何种直流分压器，ΔG17超过整定值时长的边界值均远高于0.5 ms。因此，地模波定值及防抖动元件设置时长可沿用现有设定值。

为验证本章所提行波保护定值的可靠性，设置典型区内外故障情况进行定值可靠性验证。采用本文所取定值，且考虑Ⅰ、Ⅱ型分压器传变特性对行波保护性能的影响，行波保护的动作结果如表2 和表3所示。

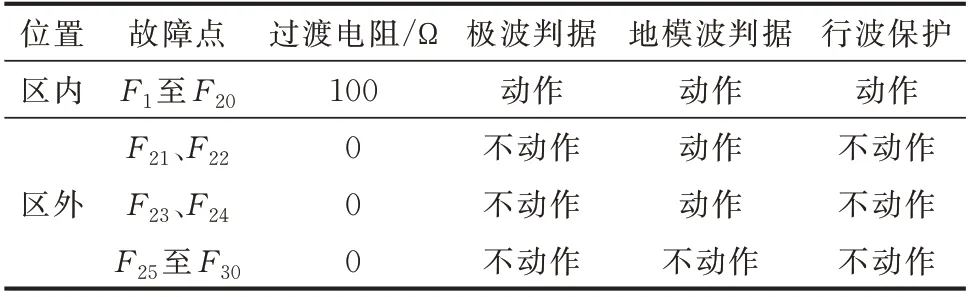
表2 采用Ⅰ型分压器时行波保护动作结果Table 2 Operation results of traveling wave protection with Ⅰtype voltage divider

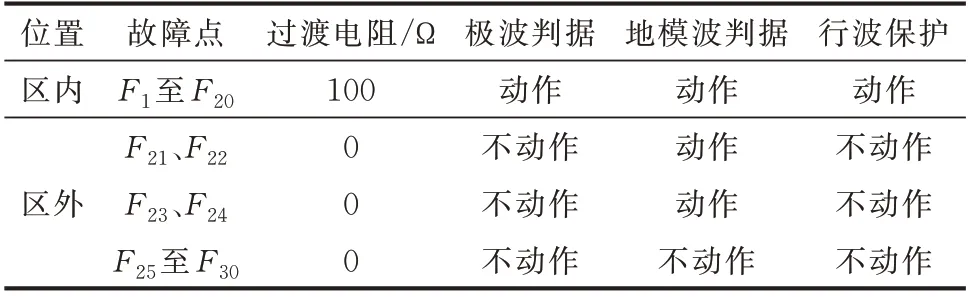
表3 采用Ⅱ型分压器时行波保护动作结果Table 3 Operation results of traveling wave protection with Ⅱtype voltage divider

由表2 和表3 可知：当采用本文所设定值时，无论考虑何种分压器传变特性的影响，行波保护在区内线路末端故障时均能可靠动作，区外故障时不误动，行波保护的可靠性得到了提高。

5 结语

本文分析了直流分压器传变特性对行波保护的影响，提出了计及直流分压器传变特性影响的行波保护定值整定方法，结论如下：

1）不同直流分压器的传变特性有所不同。Ⅰ型分压器传递函数在高频段幅值会显著下降，且其阶跃响应无超调，响应时间较长。Ⅱ型分压器传递函数在高频段幅值先上升后下降，且其阶跃响应超调量大，响应时间远短于Ⅰ型分压器的响应时间。

2）直流分压器传变特性将对行波保护性能产生影响。当采用Ⅰ型分压器时，行波保护故障特征量幅值有所下降；当采用Ⅱ型分压器时，行波保护故障特征量幅值有所上升。

3）本文提出了计及直流分压器传变特性的行波保护定值整定方法。所提方法使行波保护能有效识别区内外故障，提高了行波保护的可靠性。

本文仅针对直流分压器传变特性对行波保护及其定值整定的影响展开分析，特高压直流系统中其他涉及电压量的保护也受直流分压器传变特性的影响，后续可研究直流分压器传变特性对其他涉及电压量的保护的影响。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。