基于RHT模型的冲击荷载作用下钢筋混凝土梁动力响应分析
李广博,罗乙杰
吉林建筑大学 土木工程学院,吉林 长春 130118
0 引言
由于钢筋混凝土结构在工程应用中可能会受到极端荷载的作用(地震、爆炸、冲击等),因此,对其性能的研究一直是工程防灾领域的重点课题.国内外很多学者对冲击荷载下钢筋混凝土梁的损伤和抗弯问题从多个角度进行了研究.
Sharma等[1]人提出了车辆冲击下钢筋混凝土柱的性能评估,但试验的变量是不同的车速和车重,其推广价值有限;杨艳敏等[2]人研究了全轻混凝土梁在受冲击下的响应,从破坏形态和位移的角度进行分析,但数值模拟对照设置较少,其结论普遍性不强;Fujikake等[3]人通过对比钢筋混凝土梁在不同纵筋配筋率下的冲击落锤试验,得出高配筋率可以减少构件局部破坏的结论,但其基于碰撞过程动量守恒假设和SDOF模型进行的能量损耗计算,对实际设计能给出的有效信息很有限;查丽娟等[4]人对钢筋混凝土柱受钢球冲击进行了有限元模拟,但其钢筋与混凝土之间设置为黏结滑移,未能完全避免沙漏能带来的计算误差;李亮等[5]人的落锤试验对钢纤维混凝土配筋梁的冲击性能进行分析,得到钢纤维含量与抗冲击承载力的正比关系,不过其试验没有进行仿真模拟,未能形成高自动化体系;王天奇等[6]人对含裂纹钢筋混凝土梁进行冲击荷载下的裂纹分析,在数值模拟时采用八节点线性缩减积分,但同样并未能完全避免沙漏模式带来的计算误差.
基于以上对混凝土复杂力学行为的研究,在相关试验基础上提出RHT混凝土本构模型对于冲击荷载下低强混凝土损伤的模拟方法.通过动态摩擦理论和刚度加权罚函数法建立冲击荷载与梁的接触模型,再利用剪切变形理论和完全积分法进行显式动力学有限元计算,避免了沙漏模式[7],提高了计算的准确性,使用RHT混凝土本构模型输出的损伤因子建立的损伤评估函数,完成了对混凝土损伤的参数分析.
1 试件概况
为了讨论不同混凝土保护层厚度和箍筋间距对结构受冲击的抗弯性能和损伤影响,本文控制变量,进行了多组试验.对于每组试件的结构和尺寸,以A-300-20组试件为例进行图示说明,图1为试件命名规则,图2为试件的设计详图.

图1 试件命名和命名规则Fig.1 Specimen naming and naming rule
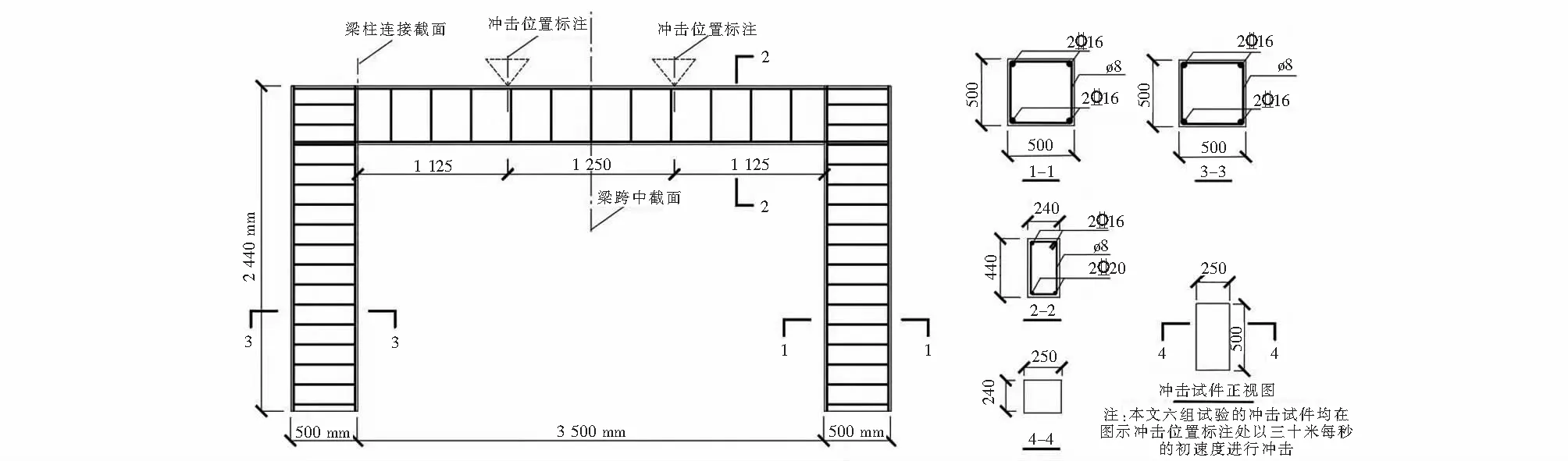
图2 试件设计详图Fig.2 Sample design diagram
如图2所示,本文6组试验的受冲击位置全部设在梁跨度三等分处,冲击试件尺寸如图2中4-4标注,试验开始时刻,2个冲击试件同时以30 m/s的速度对试件梁进行冲击.在研究混凝土保护层厚度对损伤的影响时,分别对梁柱连接截面和梁跨中截面的损伤因子分布进行了分析;在研究箍筋间距对抗弯性能的影响时,对梁跨中截面的位移进行了分析,上述两个截面在试件中的位置如图2虚线部分所示.
2 基于RHT本构模型的损伤理论
2.1 RHT本构模型损伤因子的推导
RHT本构模型的损伤假设由其强度理论[7]出发:
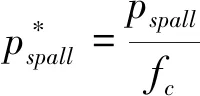
(1)
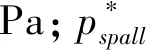
由(1)式可推出失效非弹性应变:
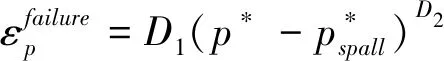
(2)
式中,D1和D2为材料常数;p*为相对于fc的标准化压力,Pa.
(2)式推出由非弹性偏应变累积的损伤因子:
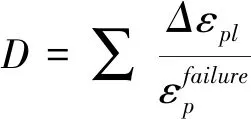
(3)
式中,Δεpl为非弹性偏应变.
2.2 损伤评估函数的建立
将截面单元损伤因子按大小进行划分,由损伤因子在截面的分布率作为损伤评估函数:
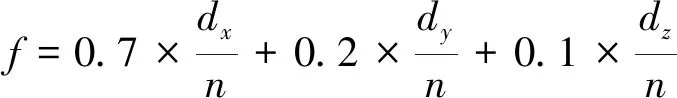
(4)
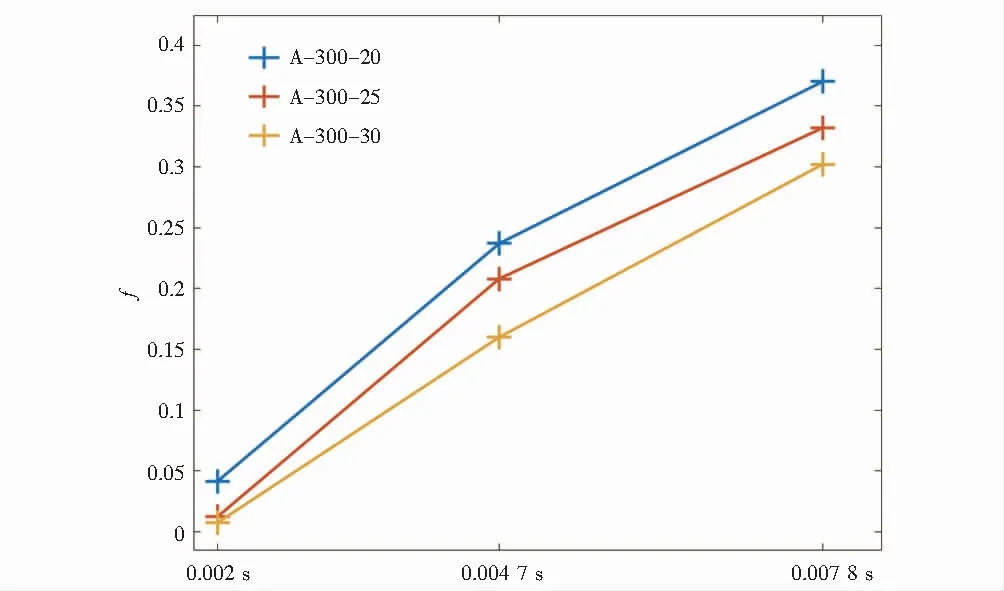
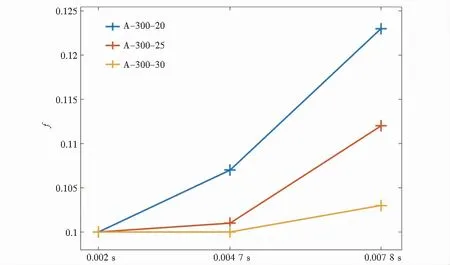
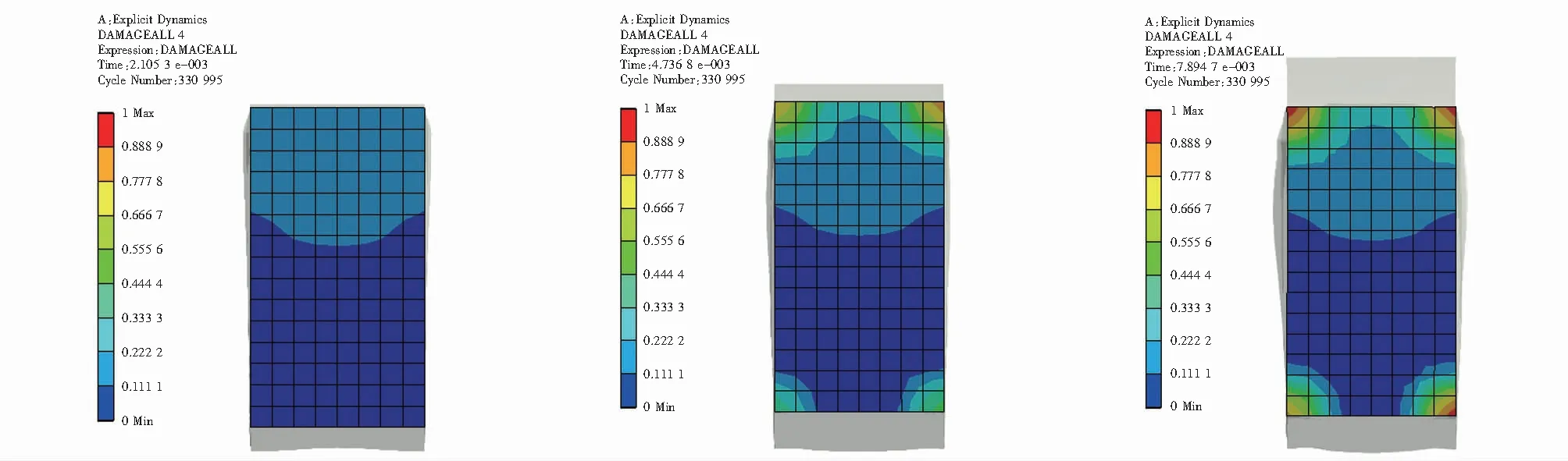
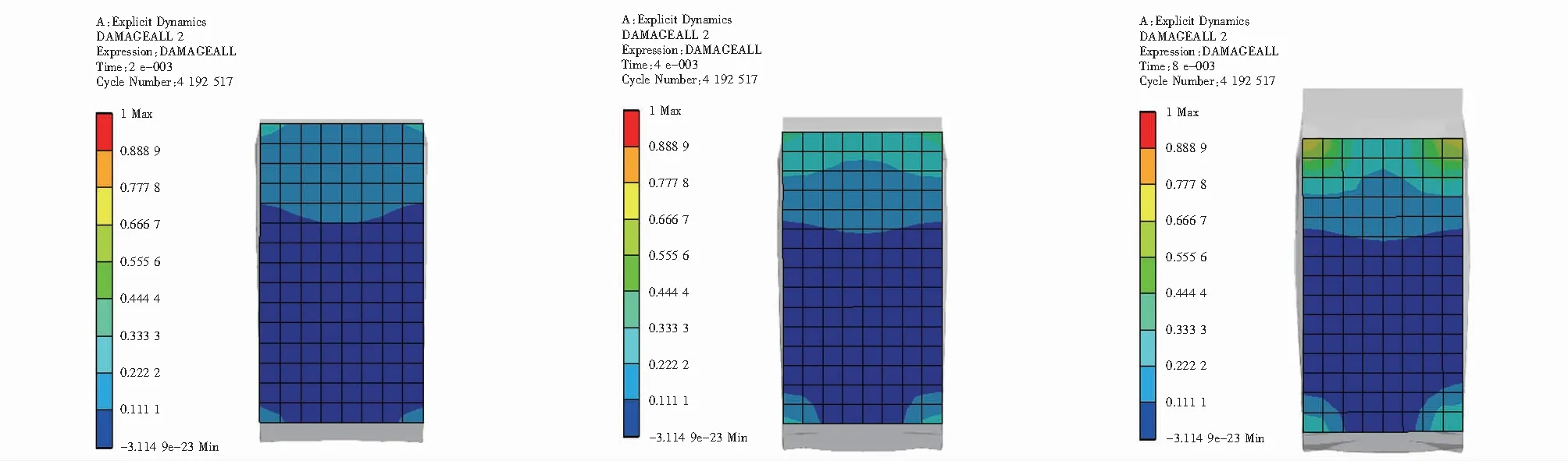
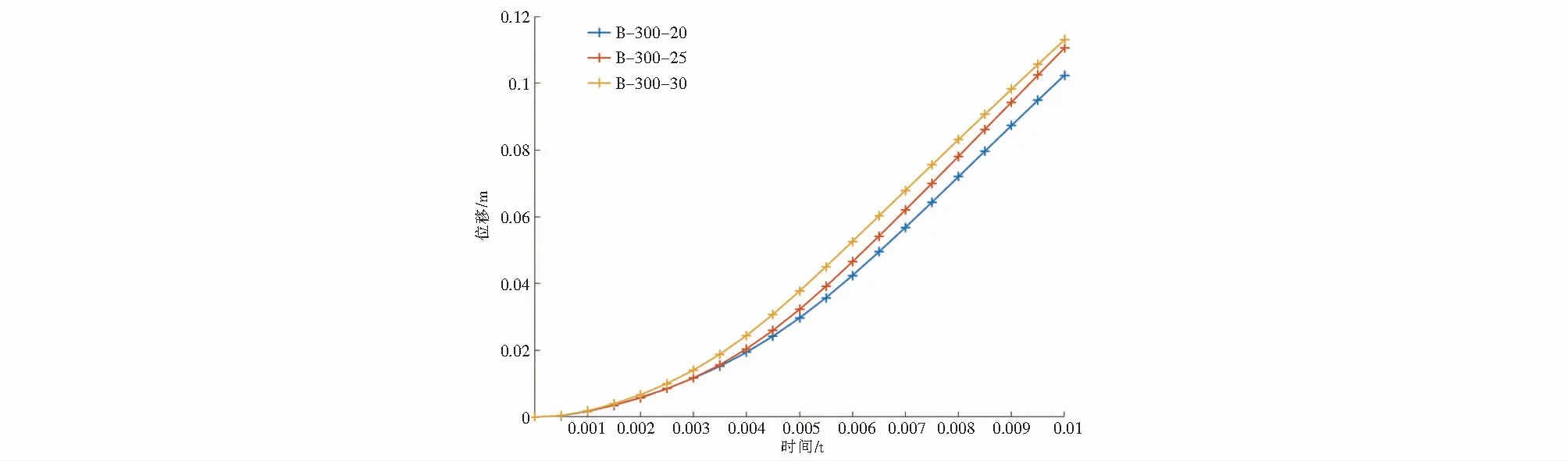
式中,dx为据式(3)得出D=1的截面单元个数;dy为据式(3)得出0.66 该损伤评估函数对3组不同大小区间的损伤因子的分布率进行加权求和,从而每一个函数值可以评估一个截面的损伤程度,函数值越大,表示截面损伤程度越高. 本文由ANSYS软件基于RHT本构模型、P-alphaEOS和PolynomialEOS方程,利用显式瞬态分析通过式(3)求解出各组试件损伤因子的分布,且求解出试件受冲击后的整体位移,再将数据通过式(4)处理,从而进行损伤分析,并提取梁危险截面处的位移进行数值分析,研究受冲击下梁的抗弯性能. 通过对比梁柱连接截面和危险截面(梁跨中截面)在不同时间下损伤评估函数值的分布,对混凝土保护层厚度对结构受冲击后的损伤进行分析. 图3 A组试件20 mm不同时间梁柱连接截面损伤因子Fig.3 Damage factors of 20 mm beam-column connection section of group A specimens at different times 图4 A组试件25 mm不同时间梁柱连接截面损伤因子Fig.4 Damage factors of 25 mm beam-column connection section of group A specimens at different times 图5 A组试件30 mm不同时间梁柱连接截面损伤因子Fig.5 Damage factors of 30 mm beam-column connection section of group A specimens at different times 图3~图5为结构中梁与柱的连接截面在0.002 s,0.004 7 s和0.007 8 s时刻的损伤因子分布. 图3~图5中标尺红色部分表示据式(3)得出时的单元格的状态,截面图下方依次为试件名、当下截面所在时刻、据式(4)计算的损伤函数数值,通过图3~图5可以清晰地看到各组在各时刻对应的损伤函数数值,绘制的折线图如图6所示. 由图6分析得3个任意时刻下,A-300-30组试件的评估函数f值都要小于其他两组,在梁柱连接截面处混凝土保护层厚度越大,混凝土损伤越小. 图6 梁柱连接截面损伤评估函数折线Fig.6 Broken lines of damage assessment function of beam-column connection section 图7 梁跨中截面损伤评估函数折线Fig.7 Broken lines of damage assessment function of beam mid-span section 图8~图10展示了各组梁跨中截面的损伤因子分布,可以看到各组在各时刻对应的损伤函数数值,绘制折线图如图7所示. 图8 A组试件20 mm不同时间梁跨中截面损伤因子Fig.8 Damage factors of 20 mm beam mid-span section of group A specimens at different times 图9 A组试件25 mm不同时间梁跨中截面损伤因子Fig.9 Damage factors of 25 mm beam mid-span section of group A specimens at different times 图10 A组试件30 mm不同时间梁跨中截面损伤因子Fig.10 Damage factors of 30 mm beam mid-span section of group A specimens at different times 据图7分析可得,在跨中截面处3个任意时刻下,A-300-30组试件的评估函数f都要小于其他两组,可以看出在跨中截面处混凝土保护层厚度越大,混凝土损伤越小.对比图6和图7也不难看出,跨中截面比梁柱连接处截面受冲击影响要小.可以通过对两个截面的分析推广到梁的所有截面可以得出,混凝土保护层厚度越厚,梁试件在冲击作用下混凝土损伤越少. 通过分析梁危险截面(梁跨中截面)的位移,探讨箍筋间距对结构受冲击后抗弯性能的影响.图11显示了3组试件在梁危险截面处位移随时间变化的具体数值. 图11 梁在危险截面处的位移曲线Fig.11 Displacement curves of beam at dangerous section 据图11分析不难看出梁在危险截面处的位移随着箍筋间距的减小而减小,由此本文可以得出:在冲击荷载作用下,箍筋间距对梁的抗弯性能存在影响,且箍筋间距越小,梁对抗冲击荷载的能量越强. (1) 建立了基于RHT本构模型损伤因子分布率的钢筋混凝土梁冲击损伤评估模型,可以直观描述某一截面的损伤. (2) 梁试件的保护层厚度与损伤的分布为反比关系,混凝土保护层厚度越厚,梁试件在冲击作用下混凝土损伤越少. (3) 箍筋间距可以显著影响钢筋混凝土的抗弯性能,箍筋间距越小,梁对抗冲击能力越强,可通过加密箍筋来提高结构冲击下的抗弯性能.3 基于RHT本构模型的数值模拟
3.1 混凝土保护层厚度对损伤的影响分析
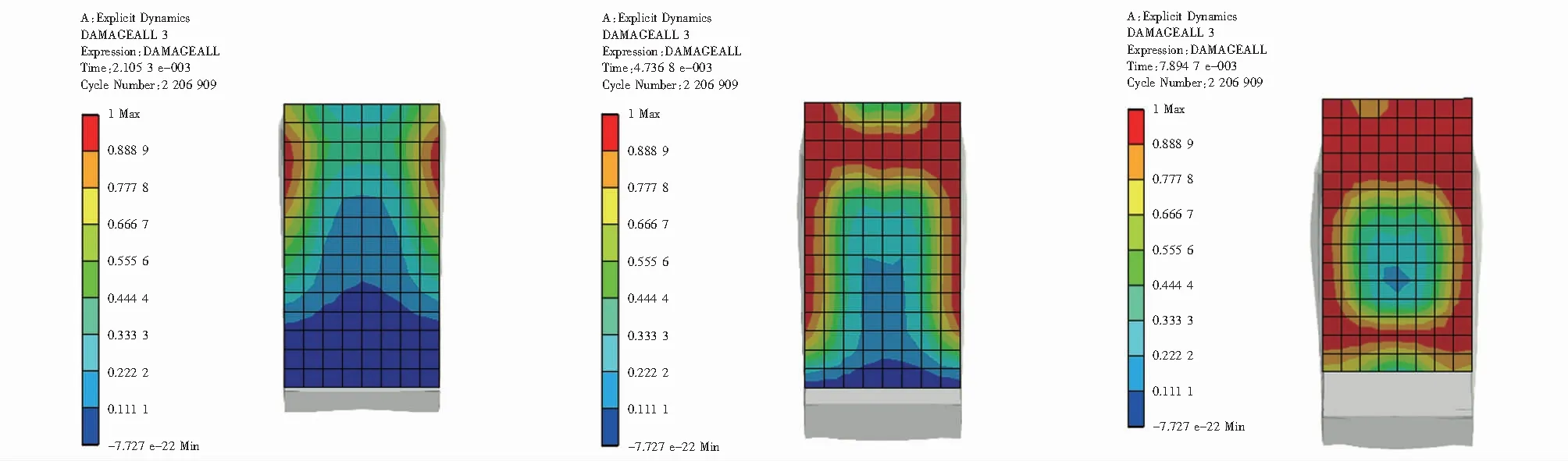

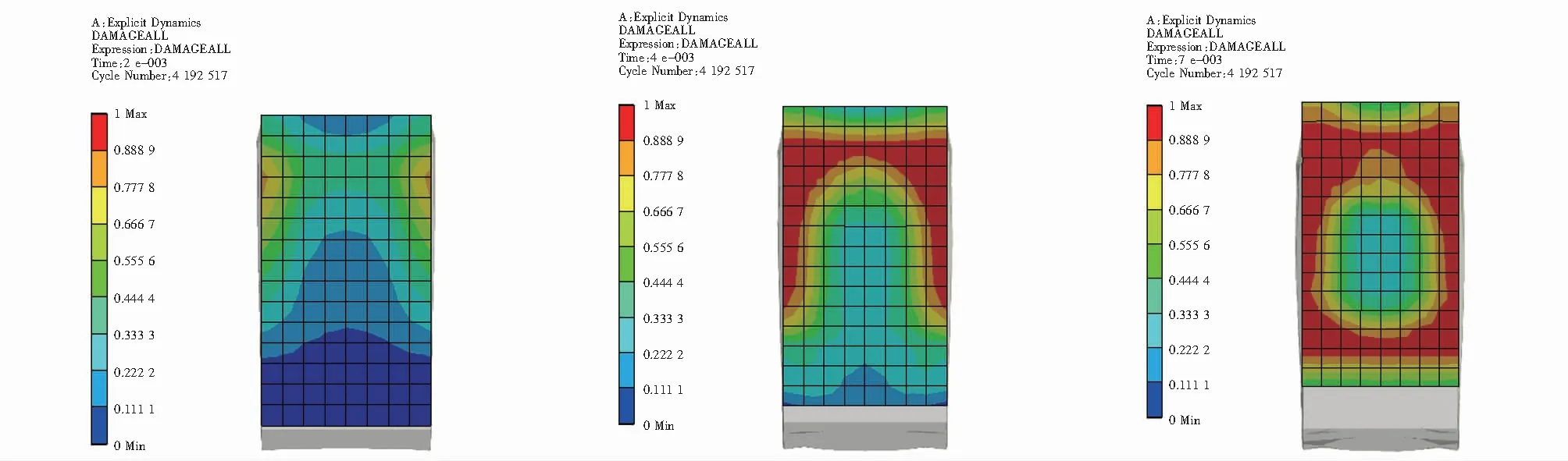

3.2 箍筋间距对抗弯性能的影响分析
4 结论

