基于ADAMS的装载机工作装置动力学仿真方法研究*

杨思源 万一品 宋绪丁

长安大学工程机械学院 西安 710064

0 引言

装载机是工程建设中土石方施工的重要机种之一，可以对物料进行反复的铲装与运输。对装载机进行动力学仿真不仅可以缩短开发周期，还能够降低开发成本。近年来，国内相关研究学者及企业设计人员对装载机等工程机械装备开展了许多动力学仿真与实验研究工作。戴跃文等[1]对反转六杆机构工作装置进行了动力学仿真分析，并采用正交试验的理论和方法对装载机工作装置进行了综合优化设计。刘晓峰[2]利用ADAMS和Ansys建立了55 t汽车起重机柔性臂架系统，对其在多种工况进行仿真分析，得到臂架系统应力及振动情况，为臂架系统和液压控制系统的设计提供依据。万一品等[3]提出了三向力销轴传感器法和动臂截面弯矩法2种工作装置载荷提取方法，并进行典型作业姿态下的载荷验证，为载荷谱编制和疲劳特性分析提供依据。

以国产9 t装载机工作装置为研究对象，利用ADAMS的Step函数对其进行铲装模拟，得到各铰点的峰值载荷以及各构件的最大应力的仿真方法。通过对其工作装置的刚体动力学分析与基于实测数据的刚柔耦合动力学仿真分析，验证了利用Step函数进行铲装仿真的合理性。为后续装载机工作装置的强度分析与结构优化提供参考依据。

1 工作装置刚体动力学仿真

1.1 几何模型与工作原理

以国产9 t装载机为研究对象，建立其工作装置三维几何模型如图1所示。

图1 装载机工作装置三维模型

在实际铲装作业过程中，一个工作循环过程可分为典型的6个作业阶段：插入阶段、崛起阶段、运输阶段、举升阶段、卸料阶段以及复位阶段[4]。在插入作业阶段，铲斗处于水平位置，动臂液压缸伸长量最短且处于锁死状态，铲斗一直向前插入物料最深处。在崛起作业阶段，摇臂液压缸伸长，将物料送入斗内，完成铲装作业。在举升作业阶段，摇臂液压缸锁死，动臂液压缸伸长，将物料举升直至卸料位置。在卸料作业阶段，动臂液压缸锁死的同时摇臂液压缸回缩，铲斗翻转，完成卸料作业。

由于物料的多样性与分散性使得铲装作业过程中工作装置受力特性复杂多变，测试每种物料的应力需要花费大量的时间、人力、物力，而通过虚拟样机技术可快速获得工作装置各铰接处的载荷。

1.2 载荷条件的确定

仿真分析时需要获得装载机工作装置所受外力变化情况，给多刚体仿真模型中添加运动副及驱动函数来模拟铲装作业。装载机作业期间，铲装作业段受力最为复杂，受到插入阻力、掘起阻力和物料重力的作用[5]。

插入阻力与物料种类、料堆高度等参数有关，其计算的经验公式为

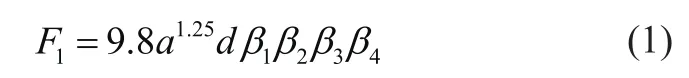
式中：F1为插入物料时铲斗所受阻力，a为插入物料深度，d为铲斗宽度，β1为物料松散度系数，β2为物料容积比系数，β3为物料堆高度系数，β4为铲斗形状影响系数。

掘起阻力计算的经验公式为

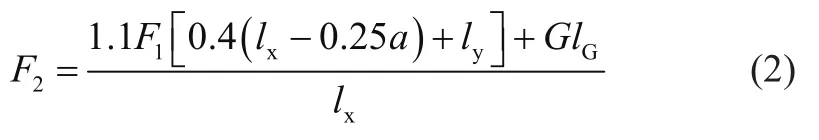
式中：F2为掘起阻力，lx为铲斗斗尖端部到铲斗与动臂铰点的水平距离，ly为铲斗斗尖底部到铲斗与动臂铰点到竖直距离，G为铲斗与其所铲装物料的重力，lG为铲斗质心到铲斗与动臂铰点的水平距离。

对各系数的取值进行选取，结合式(1)、式(2)以及工作装置的参数可得到在铲装3.3 m左右高度的散状物料时各工况下的插入阻力与崛起阻力，如表1所示。

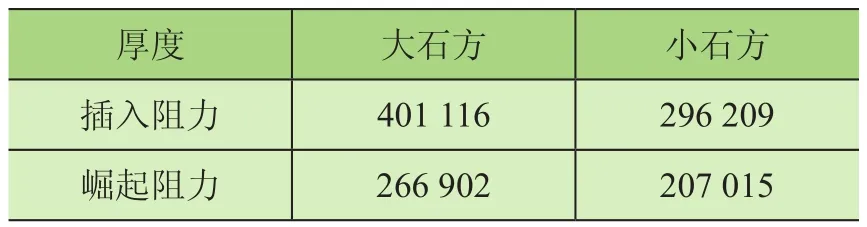
表1 不同工况下的插入与崛起阻力 N

由表1可知随着物料颗粒度的降低，插入阻力与崛起阻力均有所减小。

1.3 刚体动力学仿真分析

将工作装置的几何模型导入ADAMS中，如图2所示。对机架进行固定约束，在各液压缸体与液压缸杆之间施加滑动副，在各铰孔处添加旋转副。

图2 工作装置刚体动力学模型

在模拟铲装作业时，在铲斗中间位置施加插入阻力与崛起阻力，铲斗首先插入物料最深，然后翻转铲斗完成铲掘作业。仿真单位设置为MKS（m、kg、s），利用Step函数来添加铰点载荷和液压缸位移驱动，仿真时间设置为8 s。

在大石方工况下插入物料阶段所受阻力的Step函数为

Step(time,0,0,2.8,- 401116) +Step( time,2.8,0,3,401116) +Step( time,3,0,8,0)

掘起物料阶段所受阻力的Step函数为

Step( time,0,0,3,0) +Step( time,3,0,3.2,- 296209)

Step( time,3.2,0,6, 296209) +Step( time,6,0,8,0)

铲斗内物料重力的Step函数为

Step( time,0,0,3.2,0) +Step(time,3.2,0,6,-88200)

+Step(time,6,0,8,0)

摇臂液压缸位移的Step函数为

Step(time,0,0,3,0)+Step(time,3,0,6,-0.248)

+Step(time,6,0,8,0)

动臂液压缸位移的Step函数为

Step( time,0,0,6,0) +Step( time,6,0,7,-0.045)

+Step( time,7,0,8,-0.06)

记动臂与铲斗2个铰点分别为A和铰点B，连杆与铲斗铰点为C，由于在斗尖中点处施加载荷，且铰点A和铰点B呈对称分布，所以铰点A和铰点B的载荷相同。分别输出这3个铰点在大石方与小石方工况下的载荷时间历程如图3所示。

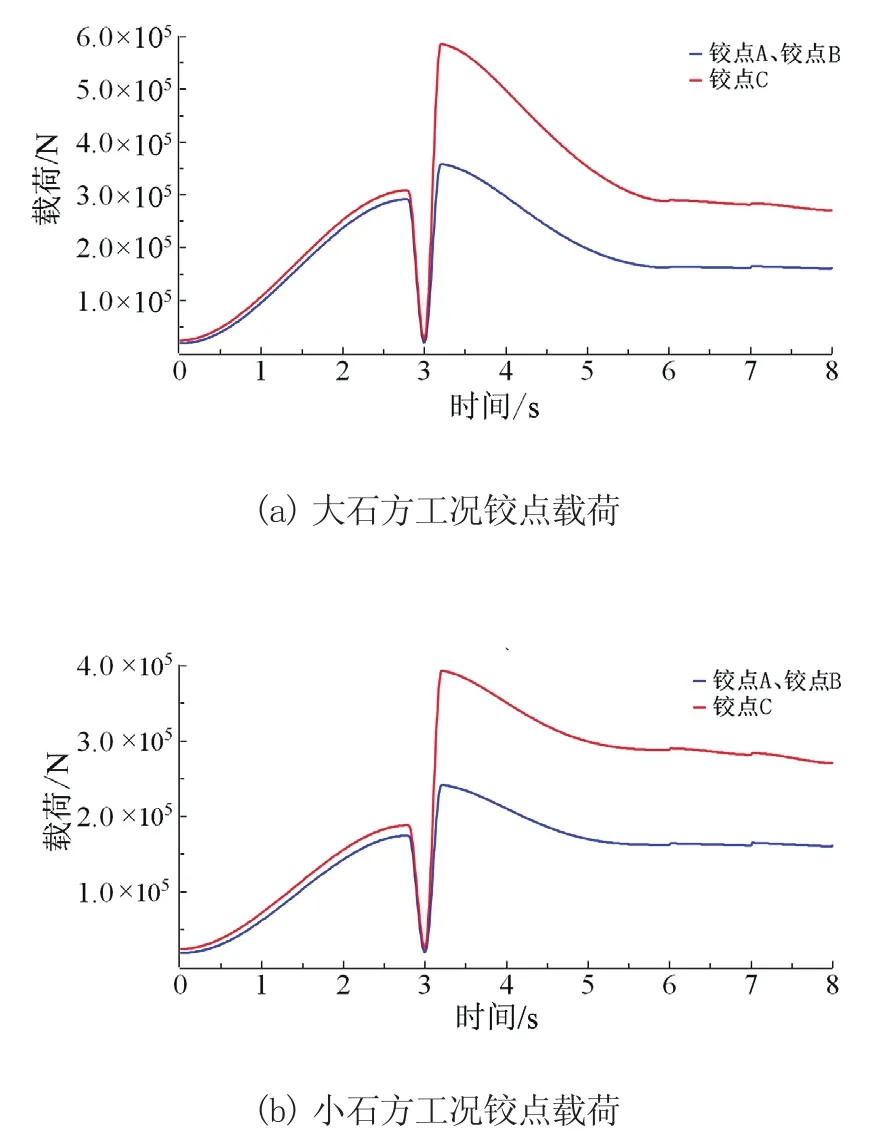
图3 不同工况下各铰点载荷

由图3可知，3个铰点的载荷呈现相同变化趋势，第一峰值与第二峰值分别由插入阻力与掘起阻力引起。其中，铰点C受力较大，在大石方与小石方工况下的峰值载荷分别为600 kN与400 kN。而铰点A于铰点B的载荷相对较小，在2个工况下分别达到358.44 kN与240.85 kN。2个工况下的实测铰孔载荷如图4、图5所示。

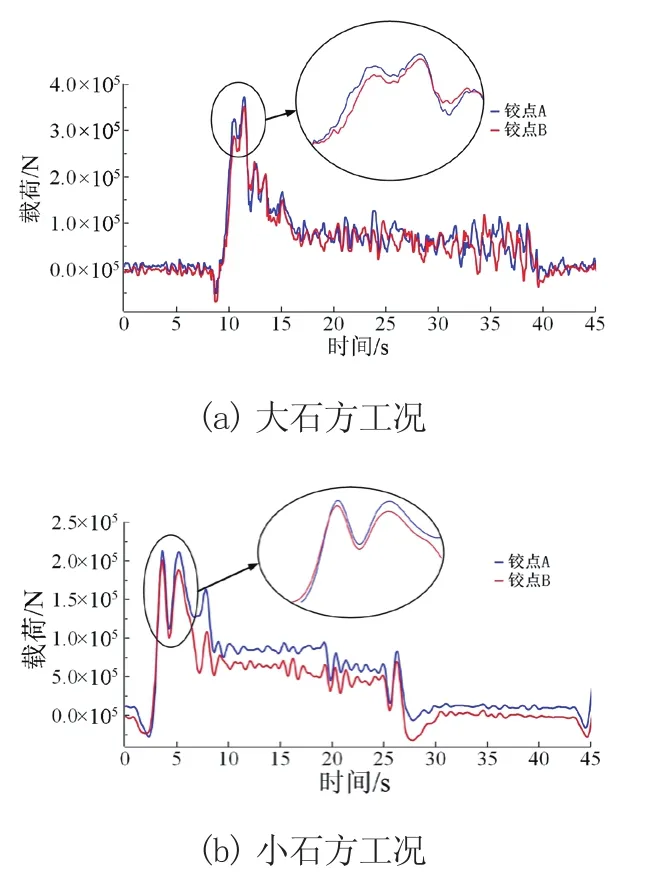
图4 A和B铰点实测载荷曲线

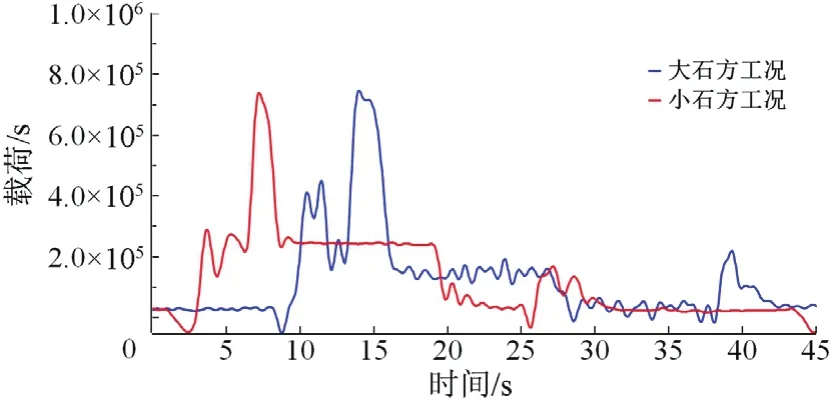
图5 C铰点载荷曲线

由图4与图5可知，在实际作业时铰点A与铰点B在不同的载荷大小有所区别，这是由于铲装物料分布不均匀所造成的偏载现象。其中铰点A与铰点B在大石方工况下的峰值载荷分别为373.20 kN和351.81 kN，在小石方工况下的峰值载荷分别为212.77 kN和200.88 kN。实测载荷与仿真结果对比如表2、表3所示。

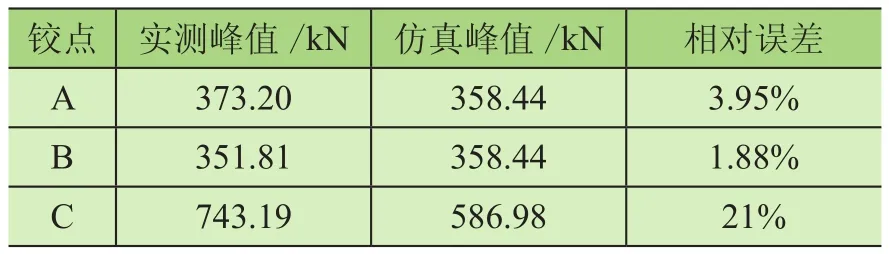
表2 大石方工况峰值载荷对比

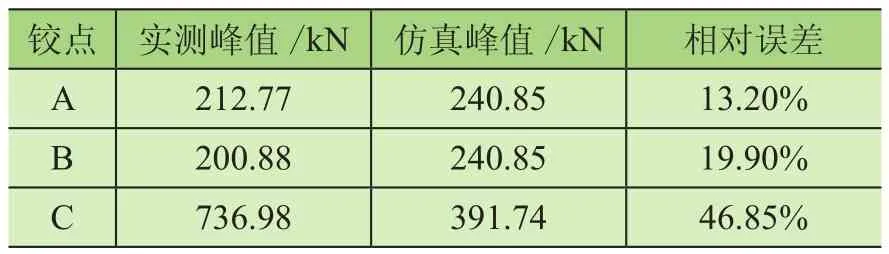
表3 小石方工况峰值载荷对比

由表1、表2可知，铰点A和铰点B的实测与仿真载荷峰值误差不超过20%，虽然铰点C的误差较大，但连杆是二力构件，受力形式单一，且装载机主要关注的受力部件是动臂，故通过动力学仿真可较好地反映动臂的受力情况。

2 工作装置刚柔耦合动力学仿真

2.1 刚柔耦合动力学模型

仿真分析的结果受所建仿真模型的准确性影响。工作装置在实际铲装作业过程中并不是纯刚体，有必要研究刚柔耦合情况下工作装置在铲装作业期间的受力情况。在实际工作中铲斗的失效形式主要为磨损[6]，可将动臂、摇臂和连杆视为柔性体，动臂液压缸、摇臂液压缸、铲斗以及机架仍视为刚性体，建立出与实际情况更为接近的仿真分析模型。

在工作装置的动力学模型中引入柔性体，利用模态叠加法计算工作装置在动力学仿真过程中的变形，可以提高动力学仿真的精度[7]。

将工作装置三维模型导入Ansys中，创建单元属性并定义材料为Q355钢，然后进行网格划分。在动臂、摇臂以及连杆铰接处建立刚性区域，如图6所示。

图6 工作装置刚性区域

提取各构件的前20阶模态，采用Craig-Bampton模态综合法来生成动力学分析所需的模态中性文件[8]。

用动臂、摇臂和连杆的模态中性文件替换刚性模型中的对应部件，建立装载机工作装置含有模态柔性体的刚柔耦合动力学模型，如图7所示。

图7 工作装置刚柔耦合动力学模型

2.2 基于Step函数的刚柔耦合仿真

利用Step函数及相同的加载位置对工作装置进行刚柔耦合动力学仿真。图8为装载机工作装置在一个工作循环下应力最大时刻下的应力云图。

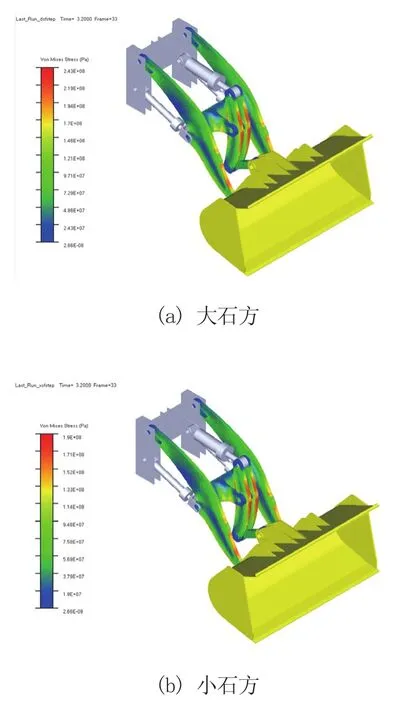
图8 工作装置应力最大时刻应力云图

由图8 可知，大石方与小石方工况下工作装置最大应力分别为242.84 MPa和189.61 MPa，均发生在3.2 s，在动臂前端及摇臂前后端，由前文可知3.2 s正是掘起瞬间，受到掘起起阻力作用。

输出各工况下最大应力时间历程如图9所示。

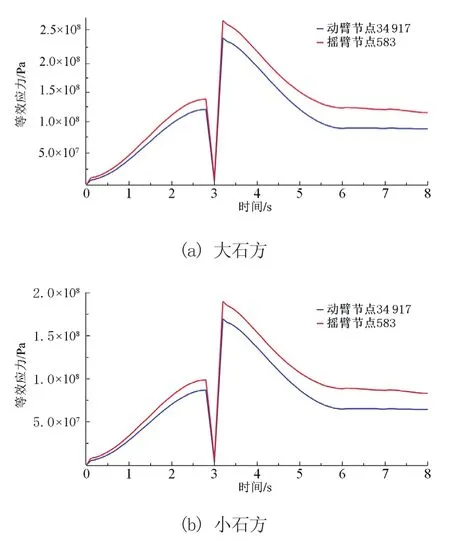
图9 工作装置应力最大节点应力时间历程

2.3 基于实测载荷的刚柔耦合仿真

将大石方与小石方的实测液压缸位移及铰点载荷导入ADAMS生成样条曲线，并将样条曲线赋予相应的驱动与铰点，大石方工况的实测液压缸位移如图10所示。

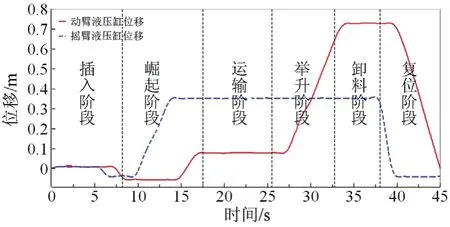
图10 液压缸位移曲线

经过仿真求解计算得到装载机工作装置最大时刻下的应力云图如图11所示。

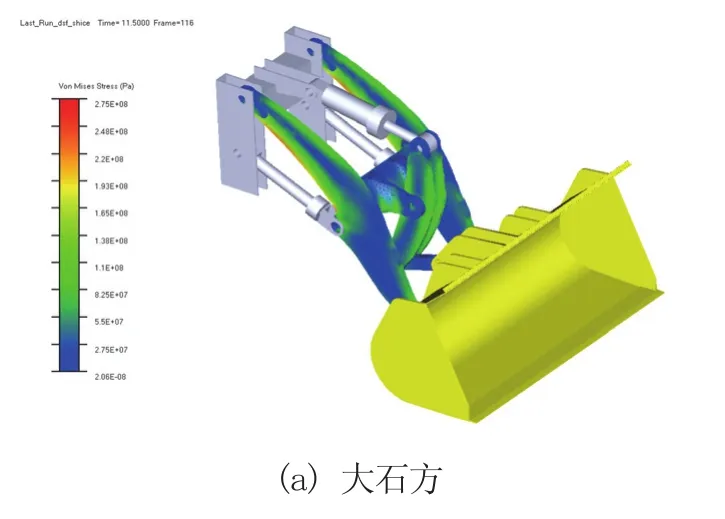
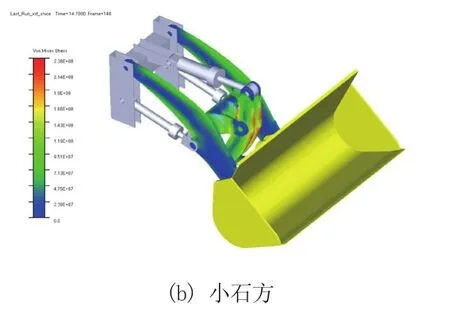
图11 工作装置应力最大时刻应力云图

由图11可知，在动臂后端与摇臂板前后端出现了较大的应力。输出动臂与摇臂在两工况下最大应力节点的等效应力时间历程如图12所示。

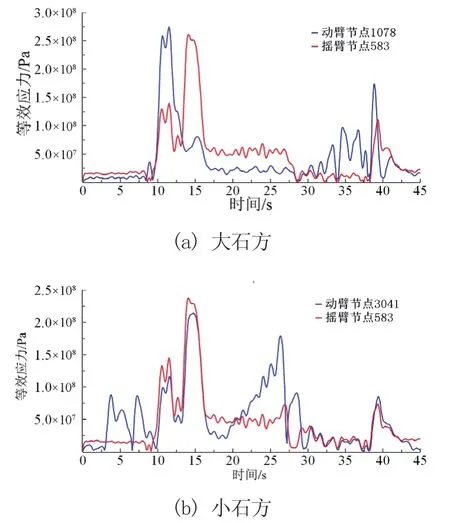
图12 工作装置应力最大节点应力时间历程

分析图12a可知在大石方工况下，动臂在插入阶段末期所受应力最大，最大应力275.07 MPa，出现在11.5 s，而摇臂在掘起阶段末期所受应力最大，最大应力为260.44 MPa，出现在14.0 s。在小石方工况下，动臂与摇臂均在掘起阶段末期14.7 s出现最大应力，最大应力分别为213.79 MPa和237.70 MPa。基于实测载荷与Step函数仿真的工作装置峰值应力结果对比如表4所示。

表4 峰值载荷对比

由表4可知基于Step函数仿真应力结果与基于实测载荷的仿真应力结果相对误差不超过26%，因此通过Step函数模拟工作装置铲装作业可较好地反映工作装置的应力大小。

4 结论

1）对额定载重9 t装载机的工作装置采用Step函数进行刚体动力学仿真，提取铰点载荷并与实测载荷对比，发现两者的峰值载荷相对误差不超过20%，验证了利用Step仿真的合理性。

2）建立工作装置的刚柔耦合模型，分别采用Step函数和实测数据进行刚柔耦合动力学仿真，结果表明，2种仿真方法之间的峰值应力的相对误差不超过26%，验证了Step函数仿真方法的正确性

3）通过仿真分析发现摇臂所受应力较大，应对其进行结构加强改进，以提高其强度。