数学实验，让学生体验更深刻

孙晶

[摘 要]数学实验丰富了学生的数学学习方式，是数学学科教学的创新实践，它具有主体性、直观性、过程性和目标性。文章以“一亿有多大”的教学实践和思考为例，提出从问题驱动、方法引领、动手操作三个方面让学生的体验有层次、有方向、有建构的教学思考。

[关键词]数学实验;学生体验;一亿有多大

[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068（2022）02-0063-03

【课前慎思】

“一亿有多大”是苏教版教材四年级下册第46至47页的内容，教师可引导学生借助比较熟悉的事物的数量来推算1亿有多大，让学生从量的角度感受1亿这个数的具体大小，增强对大数的把握能力，发展数感。

教材编排了“说一说”“数一数”“量一量”“称一称”这四个环节的活动，除了“说一说”，其他三个环节分别是让学生从时间、长度、质量三个角度去感受1亿有多大，这样一来，学生的动手操作次数过多，重复性太强，学生会觉得很无趣。能不能让学生在体验1亿有多大的过程中有选择性地进行实验操作？能不能让学生在体验的过程中获得做数学实验的思想和方法？能不能让学生在学完这节课后可以自行开展更多的体验活动？基于以上认识与思考，笔者展开了这节课的教学实践。

【教学过程】

一、谈话导入，揭示课题

师：今天这节课非常特殊，我们要借助互联网和千里之外的镇坪县的小伙伴们一起上课。

师：2019年镇坪县全县生产总值（GDP）达到24亿元。2019年5月7日，陕西省人民政府批准镇坪县退出贫困县序列，镇坪县成为安康市第一个脱贫县。

师：根据信息，你有什么想提的数学问题吗？

生1：24亿有多大呢？

师：你关注到了“24亿”。那么1亿有多大呢？谁能用数的组成知识说说1亿有多大？

生2：1亿是10个一千万。

生3：1亿是100个一百万。

……

【设计意图：本节课依托互联网，让常州和镇坪两地的学生同步上课。教师呈现了2019年镇坪县全县的生产总值，既激活了学生的已有认知，又激发了学生想深入感知1亿的实际大小的需求。  】

二、活动体验，感知一亿

1.数硬币，从时间中体验一亿有多大

师：瞧！老师带来了什么？

生（齐）：硬币。

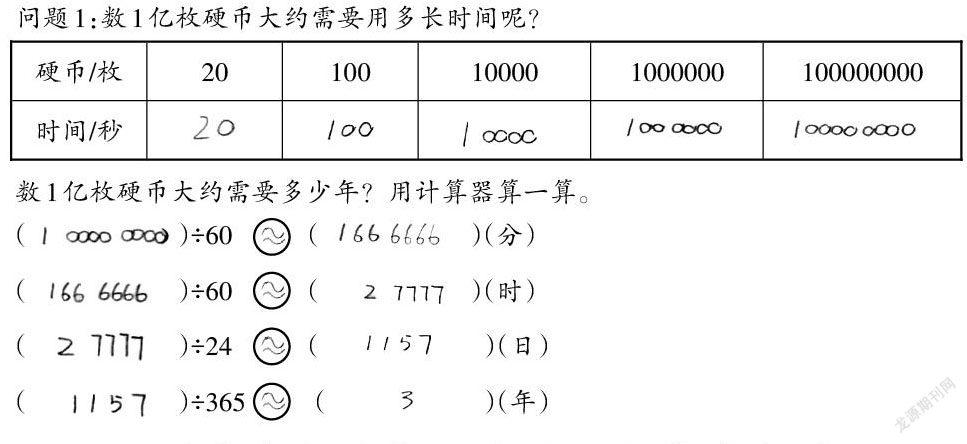
师：如果要数1亿枚硬币，一枚一枚地数，大约需要花多长时间呢？

……

师：大家的猜想都合理吗？如果让你来数，你打算怎样数？

生1：可以先数10枚硬币，再根据数10枚硬币的时间算出数1亿枚硬币的时间。

生2：先记录数100枚硬币的时间，再用1亿除以100算出时间。

……

师：怎么没有人直接数1亿枚硬币呢？

生3：直接数1亿枚硬币时间太长了。

师：是啊，1亿是个很大的数，直接数会很麻烦，所以同学们都想到了先数一部分再推算，那就用这样的办法来做实验。

出示实验要求：

（1）数一数：一枚一枚地数硬币，数20枚需要多少时间？

（2）算一算：照这样的速度，数1亿枚硬币需要多少时间？

呈现学生资源：

师：两位同学推算出的时间为什么不同？

生4：数的速度不一样。

师：观察数据，数20枚硬币的时间只相差了3秒，推算到1亿枚竟然相差了1500万秒。你有怎样的感受？

生5：刚开始相差得很小，但是随着硬币数量的增多，差距会越来越大。

……

师：你会把秒换算成较大的时间单位吗？

师：刚才我们是怎么体验1亿有多大的？

生6：我们通过数20枚硬币的时间，推算出数1亿枚硬币的时间。

师：提出问题、进行猜想、实验设计、实验操作、得到结论，这些是做实验的一般步骤。1亿是很大的数，在不能直接数的时候，我们可以用测少算多的方法去解决问题。

【设计意图：当学生推算出数1亿枚硬币所需要的时间后，教师启发他们把得到的结果换算成以“年”为单位的时间，把抽象的数转化为可感知的量，帮助学生从时间上获得对“1亿”这个数的具體感知。实验之后，教师引导学生回顾实验的过程，了解做实验的一般步骤和采用的实验方法，为接下来的学习提供脚手架。】

2.量硬币，从高度（长度）中体验一亿有多大

师：你还想从硬币的哪些方面来体验1亿有多大？

生1：我想把硬币连在一起，看看1亿枚硬币连在一起有多长。

生2：我想研究1亿枚硬币摞在一起的高度。

……

出示实验要求：

（1）选一选：选择其中一个问题展开研究。

（2）量一量：选择适量的硬币进行测量，记录数据。

（3）算一算：推算1亿枚硬币有多高或有多长。

师：对于第（1）问，老师拍了几张照片，一起来看看。

<D：＼书＼30＼小教教学参考·数学202201＼1s68.tif>

师：这些测量方法你都赞同吗？为什么？

生3：我赞同第一种和第二种，不赞同第三种，因为第三种没有对齐零刻度线。

师：我们测量的时候要规范细致、考虑全面，这样推算的结果才会合理。

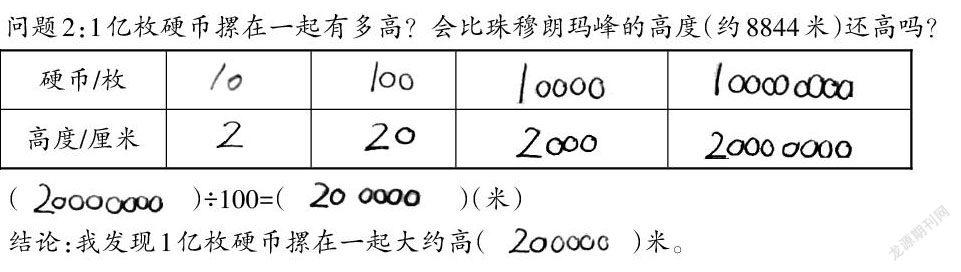
[问题2：1亿枚硬币摞在一起有多高？会比珠穆朗玛峰的高度（约8844米）还高吗？][硬币/枚 高度/厘米 ][（                         ）÷100=（                         ）（米）

结论：我发现1亿枚硬币摞在一起大约高（                     ）米。

生4：10枚硬币大约厚2厘米，1亿枚硬币大约高20000000厘米，即200000米。

师（追问）：大约是珠穆朗玛峰高度的多少倍？

生5：23倍。

……

[问题3：1亿枚硬币连在一起有多长？会比常州到镇坪的路程（约1300千米）还远吗？

生6：一枚硬币的长度大约是2.5厘米，1亿枚硬币连在一起大约长250000000厘米，是2500千米。

师（追问）：大约是常州到镇坪的路程的几倍？

生7：2倍。

……

【设计意图：教材原本只是让学生体验1亿枚硬币摞起来的高度，这里教师增加了体验1亿枚硬币连在一起的长度的环节，让学生有选择性地进行研究。在研究的过程中，教师注重规范学生的测量行为，进而培养学生思维的严谨性。学生推算之后，教师让学生用算一算、估一估的方法分别算出1亿枚硬币摞起来的高度大约是珠穆朗玛峰的多少倍，1亿枚硬币连起来的长度大约是常州到镇坪的路程的几倍，通过与参照物进行对比，帮助学生获得对1亿的实际大小的具体感知。】

三、设计实验，拓展延伸

师：除了硬币，我们还可以通过研究什么来体验1亿有多大呢？

（先让学生自由地说一说，教师再出示实验内容）

[下面的问题中，选择你最感兴趣的一个打“√”，并设计实验方案。

1亿名小学生手拉手的长度能绕地球一圈吗？（   ）

1亿张A4纸铺开的面积有常州恐龙园的占地面积大吗？（   ）

1亿碗biangbiang面大约需要多少千克的面粉？（   ）

【设计意图：教师不仅要让学生从不同的角度体验1亿的大小，还要让学生掌握数学实验的思想和方法。同時，教师引导常州和镇坪的学生寻找身边感兴趣的事物来研究、体验，并从三个问题中选择一个设计实验方案，满足学生个性化思维发展的需求。通过设计实验方案，学生可以将体验内容拓展到生活的方方面面，将学习的场所延伸到校外。】

四、回顾全课，总结反思

师：通过今天的学习，你有哪些收获？

师：这节课，我们通过做实验体验了1亿有多大。课后，我们还可以采用这样的方法去研究更多的数学知识。

【设计意图：学生的学习是一个长期的过程，教师通过引导学生回顾与反思，帮助学生巩固数学实验的一般步骤，掌握研究数学问题的实验方法，积累数学活动经验，让学生自主构建数学知识系统，并能够将数学思维由课内延伸到课外。】

【教学反思】

数学实验丰富了学生的数学学习方式，是数学学科教学的创新实践，它具有主体性、直观性、过程性和目标性。本节课教师主要借助实验工具——一元硬币，从时间和长度两个维度开展数学实验，让学生感知1亿的实际大小，引导学生借助一定的参照物来加深对1亿的直观感受，帮助学生获得研究数学问题的思想和方法，尊重学生学习的主体性。

一、问题驱动，让学生体验有目的

问题是数学的心脏，是师生之间互动最重要的载体，是点燃学生思维生长的导火线。首先，教师借助一定的数学信息引发学生对1亿到底有多大产生好奇，从而进入本课所要研究的重点。接着，教师借助硬币抛出第一个问题“一枚一枚地数1亿枚硬币大约需要用多少时间”来激发学生的探究欲望，带领学生有序地推算出数1亿枚硬币所需要的时间，将抽象的数转化为可感知的量。其次，教师引导学生思考利用硬币还可以从哪些方面体验1亿的大小，注重培养学生的发散思维，引出“1亿枚硬币摞起来有多高”和“1亿枚硬币连起来有多长”这两个问题，让学生从中选择一个展开自主探究，充分发挥学生的学习主动性和积极性。最后，教师以问题“除了硬币我们还可以通过研究什么来体验1亿有多大”让学生的思维从课堂延伸到课外。学生根据教师精心设计的问题有步骤、有目的地展开实验操作，在操作的过程中逐步加深对1亿这个数的认识。

二、方法引领，让学生体验有方向

数学实验需要合理的实验设计，合理的设计可以让学生的思考有方向、活动有顺序。在从时间上体验1亿有多大的实验过程中，教师引导学生归纳出实验的方法——测少算多，完整经历实验的一般步骤，即提出问题—进行猜想—实验设计—实验操作—得出结论，为接下来学生自主探究1亿枚硬币摞起来的高度或连起来的长度提供脚手架。另外，小学数学实验需要规范操作，教师在学生测量硬币的过程中关注其操作行为，实时收集学生的测量方法，通过对比引导学生自主发现合理的测量方法，培养学生思维的严谨性，提升学生的数学素养。

三、实践操作，让学生体验有建构

瑞士心理学家皮亚杰说过：“儿童的智慧源于操作，操作是儿童早期认识世界、适应环境、赖以生存的主要手段。儿童要认识物体，必须对它施加动作，在移动、拆散、合并物体的反复操作过程中，通过头脑与材料的相互作用与协调，建构自己的认知结构。”可见，操作活动是学生获取知识的重要途径。本节课，教师借助小小的一枚硬币作为切入点，引导学生通过一系列的实验操作活动逐步加深对1亿的大小的直观认知。通过操作，学生不仅能在原有的认知经验上构建新的认知结构，还能掌握数学实验的方法和思想，为今后进一步的研究奠定基础。

对大数的体验，学生需要在已有的经验和认知的基础上借助操作、推理、对比、想象来加强直观感受，而从量的角度感受1亿这个数的实际大小，可增强对大数的把握能力。课堂中要关注学生知识和方法的获得，更要关注学生个性化思维的生长以及情感的表达。数学实验，作为一种可观察、可操作、可重复的学习方式，越来越受到学生的欢迎，它可以让学生感受到数学的灵活、有趣、好玩，让学生真正地爱上数学。

（责编 罗 艳）