靶机零长发射过程中的刚柔耦合动力学分析

段文琪 方雄 党万腾 蒲克强 龙舒畅 姚小虎

摘要：针对无人靶机零长发射起飞的动力响应问题，基于刚柔耦合动力学建立靶机零长发射的靶机-火箭-发射架动力学模型，考虑靶机与滑块、火箭的连接接触关系及气动载荷、发动机推力的作用，分析靶机零长发射过程中机身、机翼在火箭推力冲击作用下的动力学响应，得到了靶机起飞过程中的姿态与强度特性，并探讨发射参数（油箱载荷、发射角度及重心偏差）对发射过程机身的影响。结果表明，标准发射工况下，与试飞试验数据对比，飞行速度、过载一致性良好，过载分布合理，结构动强度在材料强度许可值内。通过分析不同发射参数，发现油箱保持半油状态靶机可以进行零长发射；不同发射角度会影响靶机发射后的飞行高度，且发射角度越大，飞行高度越大，但对机身的动响应影响较小；机身重心与推力线之间的偏差对靶机零长发射的姿态影响较大，靶机在标准工况满油发射时质心不宜过低。此方法可用于无人机零长发射过程中的动力学计算，为机身结构强度设计及姿态分析提供指导。

关键词：靶机；零长发射；刚柔耦合多体动力学；动响应；发射参数

中图分类号：V222文献标识码：ADOI：10.19452/j.issn1007-5453.2022.01.006

基金项目：中国博士后科学基金（2020M672614）

火箭助推动力形式的靶机零长发射是将无人靶机固定安放在发射架导轨上，调整发射角度后打开发动机，火箭点火后在火箭大推力的作用下实现短时间加速升空起飞。当火箭燃料耗尽推力消失后助推火箭脱离机身，之后靶机利用自身发动机产生的推力继续飞行。期间，靶机机身受到瞬时的火箭推力載荷作用。要保证靶机的安全起飞，对靶机的机身结构和发射架的结构强度要求都比较高。因此，对无人机零长发射的结构冲击动力学响应问题进行研究，可以有效降低零长发射的失败次数和事故率，并保证无人机内部结构的安全[1]。

国内外许多学者对无人机的发射动力学过程进行了研究。在刚体动力学理论计算方面，周同礼[2]和裴锦华等[3]初步探讨了发射过程中如发射参数的选择、力矩平衡等问题，提供了一些设计原则和选择依据。李浩等[4]从理论上分析和计算了无人机的发射过程，重点分析了火箭脱落时刻机身的受力，仿真结果与试飞试验对比验证了无人机的高度、速度和俯仰角等数据的准确性。Liu等[5]分析了带有单个火箭助推器的小型无人机的起飞过程，考虑了助推火箭对总质量、重心和惯性的影响，通过MATLAB计算得到助推角的许可范围。刘付平等[6]对无人机火箭助推起飞进行了仿真和试飞验证，建立了发射阶段动力学模型，评估了火箭安装偏差对无人机发射的影响。张琳等[7]研究了无人机零长发射过程中无人机受到的气动力、重力等载荷的作用，并通过计算仿真表明其建立的非线性力学模型能真实反映无人机的发射状态。Eymann等[8]分析了单个火箭助推下无人机的发射过程，并结合计算流体力学方法研究了风向及重心位置偏差及发射架对起飞过程的影响，分析了火箭与发动机推力之间的相互作用。在多体动力学方面，赵志鸿[9]对无人机双火箭助推发射进行研究，用ADAMS软件对无人机发射阶段进行仿真，分析、优化了重心位置等发射参数。马威等[10]建立了无人机发射阶段的动力学模型，得到无人机的运动规律和离轨飞行的运动参数，探讨了火箭安装角和发射角对飞机动响应的影响。何敏等[11]对舰载机弹射起飞进行了多体动力学计算。通过弹射试验和刚柔耦合计算对比，试验结果与模拟结果基本吻合，从而验证了刚柔耦合模拟方法的可行性。

目前，对无人靶机发射参数、起飞后姿态等动响应的研究方法大都基于刚体，未考虑机身的柔性及附近环境等因素的耦合效应计算，火箭点火后助推瞬间对靶机的机身柔性结构动响应研究还很少。本文采用刚柔耦合多体动力学方法[12]对靶机零长发射过程进行动力学分析，得到机身发射过程中的结构动响应，讨论了不同发射参数（包括油箱载荷、发射角度及重心偏差）对发射的影响，为靶机的结构设计优化和实际发射服役时参数设置提供指导。

1数值模拟

1.1靶机刚柔耦合动力学模型

1.1.1靶机柔性体模型

机身模型采用PATRAN、ABAQUS创建靶机模态中性文件，导入到ADAMS中建立靶机柔性体部件。

机身材料主要包括铝合金、合金结构钢、玻璃纤维复合材料、碳纤维复合材料等，见表1。机身材料采用弹性本构，分别赋予各向同性壳、夹层复合壳、梁杆截面属性[13]。靶机机身长为4749mm，翼展为3400mm，机身梁框、蒙皮等结构网格尺寸约15mm，单元数量共计118836个。

1.1.2火箭与发射架

火箭质量24kg，火箭与靶机机身尾部推力锥结构形成完全包络。靶机水平放置时，柱状火箭轴线与机身纵轴方向夹角为13°。发射架是靶机起飞前的重要承力部件，由支撑结构、导轨、挡板等部件组成，火箭与发射架机构均设置为刚体，如图1所示。

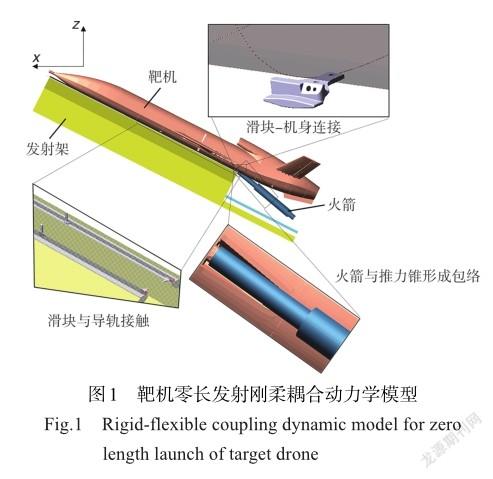
1.2载荷与边界条件

发射时，靶机先在导轨上运动，此时靶机受到的载荷包括在滑轨上受到的支持力、发动机推力、火箭点燃后的火箭推力、摩擦力、闭锁机构的闭锁力和气动载荷等。

1.2.1靶机气动载荷

1.2.2飞机发动机推力

靶机零长发射过程中发动机推力根据转速与推力的对应关系，可确定发动机推力为1911N。

1.2.3火箭推力

根据火箭推力试验得到火箭的推力曲线如图2所示。在ADAMS中用AKISPL插值函数沿推力线方向加载在火箭质心处。

1.2.4闭锁机构

为保持靶机在点火前机身稳定，且在点火后能顺利突破闭锁机构安全飞出，在模型中添加固定副并设置传感器模拟闭锁机构，闭锁力大小为4000N。

1.3工况设置

依据飞控方面的要求，靶机零长发射过程的仿真时间设置为3s，采用ADAMS动力学算法、Gstiff积分求解器，设定求解步长为0.006s。工况设置见表2。

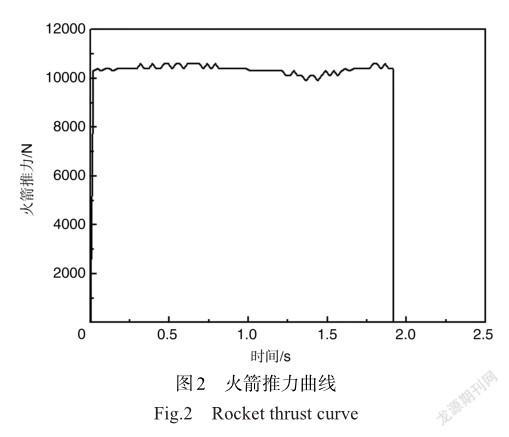
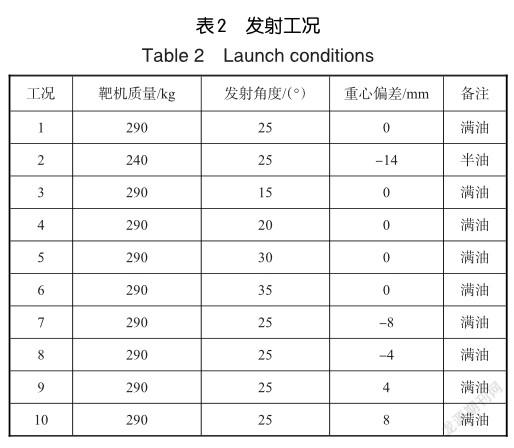
工况1为标准发射工况下的模拟计算。为研究具有不同载荷（油量及其他任务载荷）作用下靶机的动响应规律，设置了靶机油箱载荷为半油起飞的工况2。为研究不同发射角对靶机发射的影响设置了三组不同发射角度的工况，工况4～工况6设置了不同的发射架发射角度；工况 7～工况10为研究靶机质心位置偏离火箭推力线距离对靶机发射过程机身动响应的影响规律设置了6组不同偏离距离的工况。

2结果分析

2.1姿态

靶机零长发射仿真模拟过程中，火箭在点火后产生巨大推力，靶机在导轨上滑动，滑出导轨后靶机继续在空中飞行直至火箭脱离完成发射任务。ADAMS中发射过程中火箭脱离过程如图3所示，火箭轴线与靶机纵轴夹角小幅增大，然后安全分离。

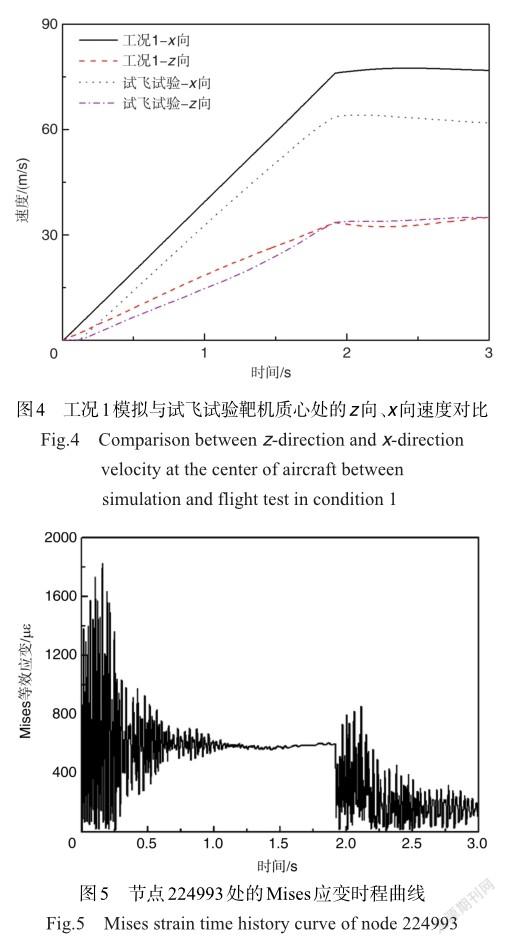
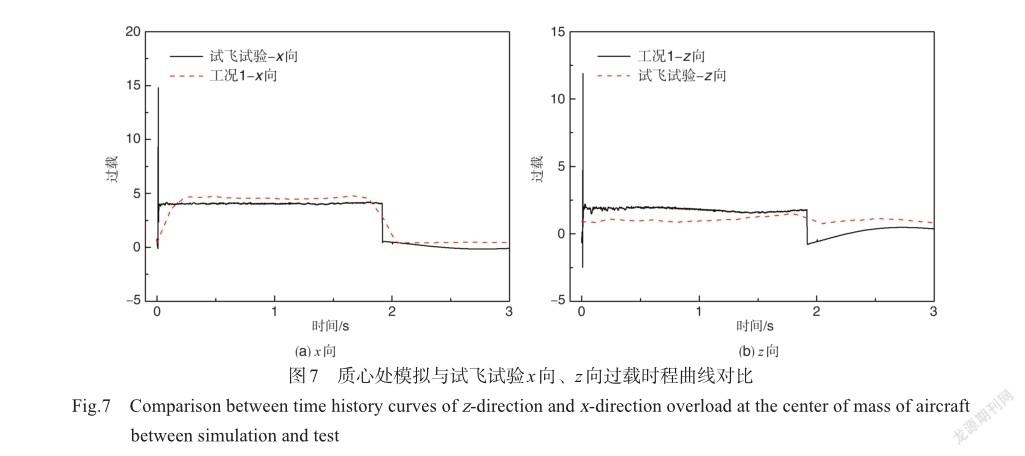
模拟与试飞靶机的z向、x向速度对比如图4所示。从图中可以发现，在零长发射模拟过程中，在1.918s时靶机的z向速度由0m/s加速至33.5m/s，x向速度增至76.0m/s，此时火箭燃料耗尽，推力消失，速度曲线出现拐点，靶机速度大小基本保持不变。与试飞结果相比，仿真下靶机的速度曲线与试飞一致性较好，均由加速阶段转变为火箭推力消失后的稳定阶段，验证了仿真结果的可靠性。因火箭助推过程中火箭推力的不稳定性，且靶机受到的x向载荷分量较大，飞行速度、位移大于z向，故产生较大的偏差。

2.2强度

零长发射过程中最大应力为248.376MPa，在发射后的0.158s出现，位于3号框与4号框之间的机身腹部节点，此处应力过大是因为有一较大任务载荷等效质量点作用于此。其他的大应力峰值也出现在发射的瞬时时刻，且位于具有任务载荷作用的位置。应变峰值出现的节点与应力峰值所在节点一致，最大为节点224993处的1825με，其应变时程曲线如图5所示。应变的曲线变化与应力趋势较一致，在发射的时刻出现较大波动且應变峰值较大，火箭推力消失后，应变值出现间断式下降。

2.3过载

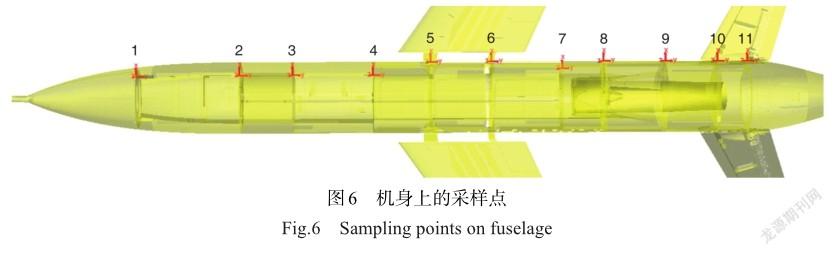
为得到靶机在零长发射过程中机身过载的传递规律，沿着机身纵轴，在机身的各个隔框与传力大梁的连接处建立Marker点并编号。靶机机身上的11个采样点分布如图6所示。

因采样点与质心处的过载曲线形状趋势类似，因此只给出质心处的过载时程曲线，并与试飞数据对比如图7所示。从图中可以看出，过载峰值出现时刻集中在发射时刻的0.01s附近，此时火箭推力的瞬时载荷作用于火箭，并通过接触作用于靶机，造成其瞬态的冲击。随着推力载荷的稳定，靶机质心处的过载瞬时下降，x向过载降至4左右，z向过载为2左右。当火箭推力消失火箭脱离后，靶机x向、z向过载进一步减小至0.5附近。与试飞结果对比，过载变化幅值与趋势基本一致，由于试飞数据加速度传感器采集间隔时间为0.2s，故在点火发射时刻未能采集到发射阶段的过载峰值时刻。

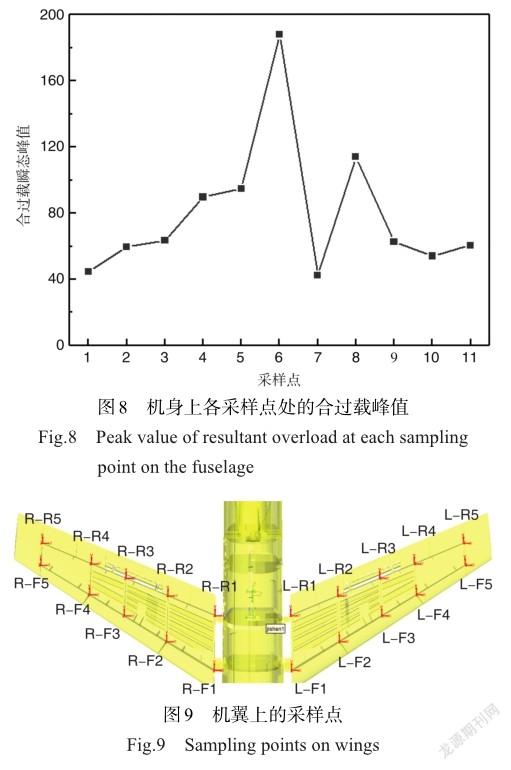
各位置的合过载瞬态峰值如图8所示，靶机的大过载峰值集中在6号框和8号框。6号框过载最大为188.1，此处接近机身质心，有气动载荷的直接作用。8号框机身腹部为火箭推力锥结构，合过载峰值为114.1，火箭推力的冲击荷载直接作用于此。在远离荷载作用位置的机头机尾两端，过载峰值小于中机身。

同理，沿着机翼前后主梁方向，从内至外，在机翼上加强肋与主梁连接处取点并编号。靶机左右机翼上采样点的分布如图9所示。提取机翼上各位置处的合过载瞬态峰值如图10所示，在1～2号采样点位置均表现出由内至外大幅衰减，左翼前梁（L-F）在4号点增大后又迅速减小，右翼前后梁（R-F、R-R）在4、5号点也小幅度增大。由于火箭推力作用于后机身的腹部，机翼前梁在接近机身的1～3号位置上合过载峰值小于后梁。

3参数讨论

3.1油箱载荷

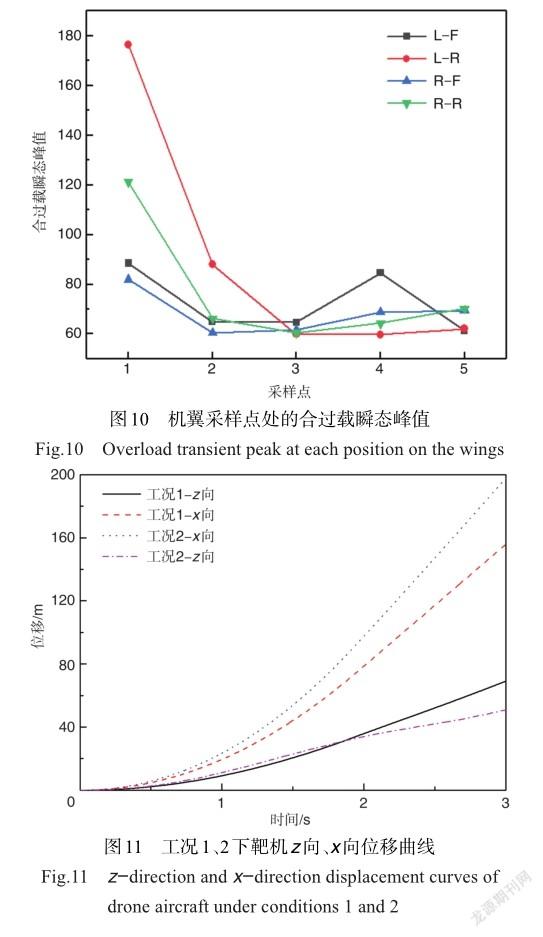
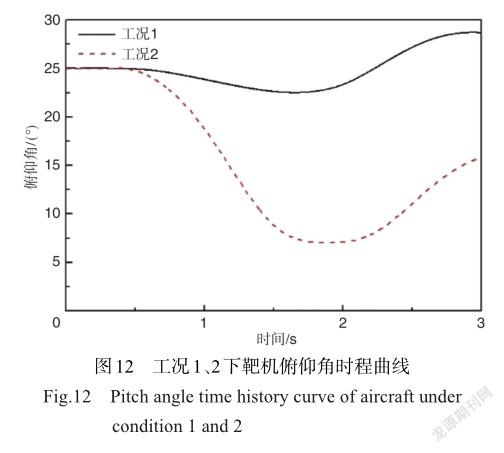
若靶机油箱保持半油（50kg）起飞，靶机的质量会大幅减小（减小50kg），质心会因此降低，与推力线会产生偏差，且未通过调节配重分布完全消除偏差。工况2针对这一发射工况进行了仿真计算。图11是工况1与工况2下x、z两方向的位移对比。计算结果表明，靶机质量及质心位置的降低会影响靶机发射3s内的z向位移（即高度）和x向位移（即飞行距离）。由于质心位置的降低（质心与火箭的推力线z向距离近14mm），火箭推力对靶机产生一个俯仰偏心力矩，以致靶机的俯仰角在靶机滑出导轨后迅速减小，最小为7°，如图12所示。靶机的飞行高度较工况1的69.1m下降至50.8m；由于靶机质量减轻，x向速度也略有增大，x向飞行距离由155.6m增大至197.7m。

3.2发射角度

为适应不同的任务目标，如达到飞行高度，靶机可以不同的发射角度进行零长发射。在以不同的发射角起飞时，靶机的飞行姿态、过载及强度不一，为得到其中的规律，工况3～工况6设置了4组不同的发射角度工况。

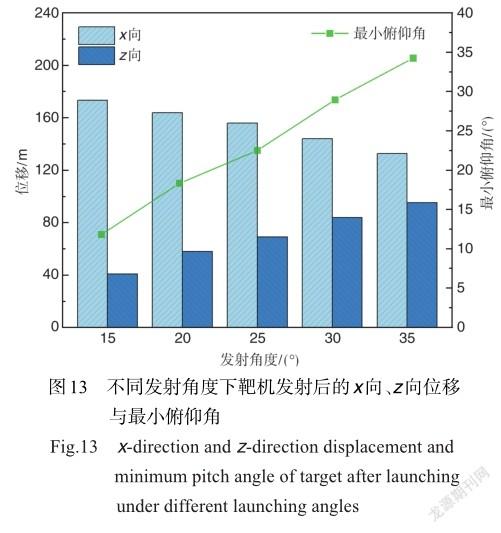
图13是靶机在不同发射角度下的3s后x向、z向位移和最小俯仰角。可以发现，x向位移与z向位移随角度增大的趋势正好相反，x向位移随角度增大而减小，z向位移随角度的增大而增大。这与靶机所受火箭推力及发动机推力等荷载在相应方向分量的变化相关，发射角度越大，靶机所受推力在z向的分量就越大。这表明，若需要适应不同的飞行训练任务高度，可通过改变不同的发射角度实现。另外，发射过程中靶机的最小俯仰角近似随发射角度线性增大。

图14是不同发射角度工况下靶机机身最大应力与质心处的过载峰值对比。由图14发现，不同发射角度工况下，靶机机身上的最大应力在230～250MPa之间，质心处的过载峰值在15～19之间，均在25°发射角时最大，最大应力与过载峰值随角度大小变化的趋势类似。

3.3质心偏差

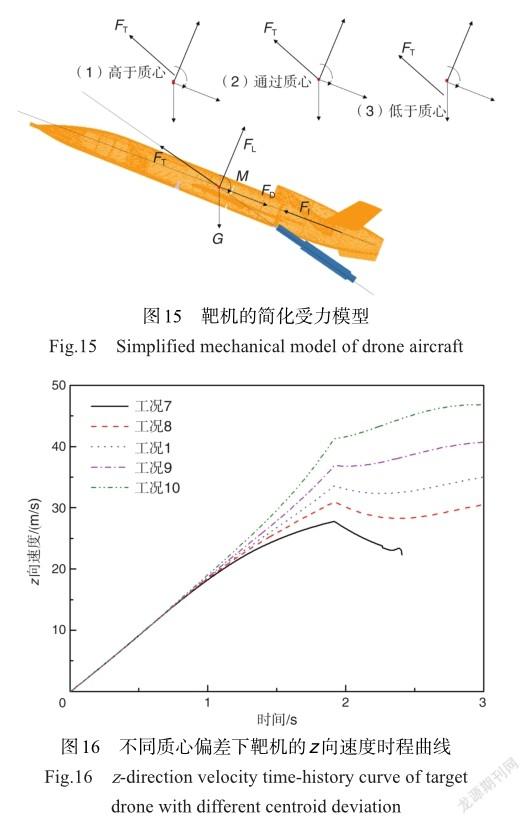
在水平放置时，发射前火箭推力线方向一般经过靶机的质心，以避免在之后的飞行过程中产生偏向力矩，造成靶机的大角度俯仰、偏航或滚转。靶机发射时，一般需要保持一定的发射安装角度，在抬升靶机的过程中，可能由于油箱油液面的改变、装置间的间隙造成靶机质心的小幅改变，从而与火箭的推力线有一定的偏差。如图15所示的靶机-火箭的简单受力模型，说明了三种推力线与质心的偏差情况。工况7～工况10为探讨与推力线具有不同偏离距离对靶机发射后动响应的影响。值得注意的是，在起飞时若推力线与靶机有小幅偏差距离，可通过调节配重质量减小偏差距离。

图16是靶机在质心与火箭推力线具有不同偏差距离工况下计算得到z向方向速度时程曲线。随偏心距离由-8mm增大到8mm，z向速度在火箭推力消失时刻的速度逐渐增大，x向速度则相反。

图17是靶机俯仰角的变化时程曲线，工况7与工况8由于质心位于推力线下方，火箭推力与发动机推力引起的偏心力矩会使靶机的俯仰角相较于标准工况1在1～2s内减小得更快，在推力消失后再逐渐增大。与此相反，工況9与工况10质心位于推力线上方，推力产生的偏心力矩使靶机在离开滑轨后俯仰角在1～2s内增大，工况10中在2.5s左右达到40.1°后，在气动力矩的作用下才开始减小。

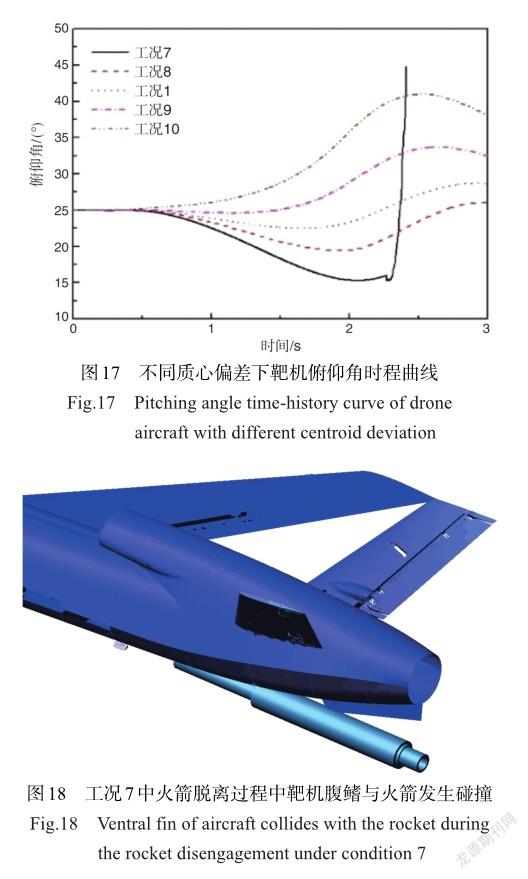
需要说明的是，在工况7中，因靶机质心在推力线下方具有8mm的偏离，偏心力矩过大导致机身俯仰角大幅减小。在火箭在推力消失后的脱离过程中，靶机俯仰角开始增大，导致火箭与后机身腹鳍发生刚性碰撞，如图18所示，造成机身姿态角发生急剧变化以致计算中止。因此，靶机满载发射时，应尽量避免推力线在靶机质心位置上方偏离太大。

4结论

本文建立了靶机-发射架-火箭刚柔耦合多体动力学模型，计算结果表明，标准满载工况进行零长发射，靶机的z向速度、z向位移和过载时程曲线与试飞一致性较好，过载峰值出现在发射的初始时刻。机身上过载的传递路径为沿着主梁从后机身火箭推力锥所在的8号框向前后机身衰减。机身应力应变分布合理，满足靶机结构材料强度设计要求。此方法可广泛用于类似机型试飞前的仿真预试验。通过对不同发射参数下的工况进行零长发射仿真计算，得出以下几点结论：

（1）靶机半油工况可以进行零长发射，由于靶机质心偏差和机身质量减轻，飞行高度较满油工况会下降，飞行距离则会增加。

（2）靶机可以以不同的角度进行零长发射，仿真完成后的飞行高度与发射角度相关，发射角度越大，发射3s后的飞行高度越大，机身的动响应变化较小。

（3）靶机机身质心与推力线之间的偏差对靶机零长发射的姿态影响较大，推力线偏离质心引起的偏心力矩直接影响发射过程中靶机的俯仰角变化，推力线位于质心上方导致靶机俯仰角减小，以致飞行高度降低；位于质心下方，则造成俯仰角增大，增加飞行高度。因此，质心偏离推力线方向不宜过大。

参考文献

[1]刘小川，王彬文，白春玉，等.航空结构冲击动力学技术的发展与展望[J].航空科学技术，2020，31（3）：1-14. Liu Xiaochuan， Wang Binwen， Bai Chunyu，et al. Progress and prospect of aviation structure impact dynamics[J]. Aeronautical Science & Technology， 2020，31（3）：1-14. （in Chinese）

[2]周同礼.某型无人机发射段飞行轨迹研究[J].南京航空航天大学学报，1988（3）：49-57. Zhou Tongli. A study of the flight trajectory pilotless aircraft in the launch posture[J]. Journal of Nanjing University of Aeronautics &Astronautics， 1988（3）： 49-57. （in Chinese）

[3]裴锦华，吴泊宁.大型无人机双发火箭助推发射技术的研究[J].南京航空航天大学学报，1999（3）：103-106. Pei Jinhua， Wu Boning. Research on launching technology for heavy pilotless aircraft with double booster rockets[J]. Journal of Nanjing University of Aeronautics & Astronautics， 1999（3）： 103-106. （in Chinese）

[4]李浩，肖前贵，胡寿松.火箭助推无人机起飞发射段建模与仿真[J].东南大学学报（自然科学版）， 2010，40（S1）：136-139. Li Hao， Xiao Qiangui， Hu Shousong. Modeling and simulation of UAV launching by rocket booster process[J]. Journal of Southeast University （Natural Science Edition）， 2010， 40（S1）： 136-139. （in Chinese）

[5]Liu B，Fang Z，Li P，et al. Takeoff analysis and simulation of a small scaled UAV with a rocket booster[J]. Advanced Materials Research，2011，12：86.

[6]刘付平，郑耀，谢芳芳，等.助推火箭安装偏差对小型无人机发射安全的影响[J].哈尔滨工程大学学报， 2018，39（8）：1343-1348. Liu Fuping， Zheng Yao， Xie Fangfang， et al. Effects of a booster rocket installation deviation on the launch safety of a smallunmannedaerialvehicle[J].JournalofHarbin Engineering University， 2018， 39（8）： 1343-1348. （in Chinese）

[7]张琳，龚喜盈，张晓辉.火箭助推零长发射建模仿真研究[J].火力与指挥控制， 2019，44（8）：150-154. Zhang Lin， Gong Xiying， Zhang Xiaohui. Modeling and simulation research on rocket boosted zero- length launching[J]. Fire Control & Command Control， 2019， 44（8）： 150-154.（in Chinese）

[8]Eymann T，Martel J. Numerical investigation of launch dynamics for subscale aerial drone with rocket assisted take-off（RATO）[C]//U.S.Air Force T&E Days，USA，2008.

[9]赵志鸿.某型无人机双发火箭助推发射动力学建模与仿真研究[D].南京：南京理工大学， 2007. Zhao Zhihong. Research on launching dynamic modeling and simulation of a certain UAV with double booster rockets[D]. Nanjing： Nanjing University of Science and Technology， 2007.（in Chinese）

[10]马威，马大为，崔龙飞，等.某无人机火箭助推发射段动力学仿真[J].四川兵工学报，2013，34（10）：32-36. Ma Wei， Ma Dawei， Cui Longfei， et al. The dynamic simulation on launching phase for unmanned aerial vehicle with rocket booster[J]. Journal of Sichuan Ordnance， 2013， 34（10）： 32-36.（in Chinese）

[11]何敏，朱小龙，刘晓明，等.舰载机前机身结构地面弹射冲击响应[J].航空学报， 2018，39（5）：125-135. He Min， Zhu Xiaolong， Liu Xiaoming， et al. Impact response of ground ejection of front fuselage structure of carrier-based aircraft[J]. Acta Aeronautics et Astronautics Sinica， 2018， 39（5）： 125-135. （in Chinese）

[12]周昊，宋亞丽，冯志杰，等.基于ADAMS的弹射座椅弹射出舱姿态研究[J].航空科学技术，2021，32（2）：66-73. Zhou Hao， Song Yali， Feng Zhijie， et al. Research on ejection attitude seat based on ADAMS[J]. Aeronautical Science & Technology， 2021， 32（2）： 66-73. （in Chinese）

[13]杨全，谭玉生.虚拟试验在飞机结构强度试验中的应用及验证[J].航空科学技术，2020，31（9）：53-58. Yang Quan， Tan Yusheng. Application and verification on virtual testing in aircraft structure strength test[J]. Aeronautical Science & Technology， 2020， 31（9）： 53-58. （in Chinese）

Rigid-Flexible Coupling Dynamical Analysis During Zero-Length Launch of Drone Aircraft

Duan Wenqi1，Fang Xiong2，Dang Wanteng2，Pu Keqiang2，Long Shuchang1，Yao Xiaohu1

1. South China University of Technology，Guangzhou 510640，China

2. AVIC Chengdu Aircraft Industrial（Group）Co.，Ltd.，Chengdu 610092，China

Abstract： To solve the dynamic response of unmanned drone during zero-length launch， based on the rigid flexible coupling dynamics， the aircraft-rocket-launcher dynamic model of zero-length launch is established. Considering the connection between the aircraft and the slider， the contact between the drone and the rocket， the aerodynamic load and the engine thrust， this paper analyzes the dynamic response of the fuselage and wings under the impact of the rocket thrust during zero-length launch， obtained the attitude and strength characteristics of the target aircraft during take-off， and discussed the influence of launch parameters （fuel tank load， launch angle and gravity center deviation） on the fuselage. The results show that under the standard launch condition， compared with the flight test data， the flight speed and overload have good consistency， the overload distribution is reasonable， and the structural dynamic strength is within the allowable value of material strength. Through the analysis of different launch parameters， it is found that the aircraft can be launched with zero length when the fuel tank is kept at half oil state. The Larger the launch angle is， the higher the flight altitude is， but the influence on the dynamic response of the fuselage is small； The deviation between fuselage center of gravity and thrust line has a great influence on the zero-length launch attitude of the aircraft， and the center of gravity should not be too low when the target is launched with full oil under standard condition. The method can be used in the dynamic calculation of aircraft zero-length launching process and provide guidance for fuselage structure strength design and attitude analysis.

Key Words： target drone； zero-length launch； rigid-flexible coupling multi-body dynamics； dynamic response； launch parameters

3198500338264