典型螺栓连接件的随机振动多模型灵敏度分析

袁修开 赵超帆 郑振轩 孔冲冲

摘要：为分析组合模型输出响应不确定性的来源及其影响，本文提出多模型合并下的方差灵敏度和矩独立灵敏度指标及其分析求解方法。模型方差灵敏度量化了各单模型对组合模型输出响应方差的影响。模型矩独立灵敏度则量化了各模型对组合模型输出响应的概率密度函数的影响。同时，本文还给出了两种模型灵敏度的求解方法。最后，以航空典型螺栓连接件为例，分析了连接件随机振动响应模型合并预测的灵敏度。结果表明，影响组合模型灵敏度的主要因素为组合模型的权重值以及各单模型本身的不确定性（模型内部参数引起）。

关键词：灵敏度分析；组合模型；不确定性；随机振动

中图分类号：TH113.1文献标识码：ADOI：10.19452/j.issn1007-5453.2022.01.014

基金项目：航空科学基金（20170968002）；中央高校基本科研业务费专项资金资助项目（XMU20720180072）

螺栓连接在航空工程结构中被广泛应用。在仿真建模中，螺栓结构由于机理复杂而常被简化处理，而简化或者假设不同，所建立的模型也会有所不同。那么从一组不同的模型形式中进行选择就伴随着不确定性，这种称为多模型下的模型形式不确定性[1]。模型形式不确定性来源于人们对问题认识的不足，导致所建立的模型不能完全反映出现实问题，而模型的合并预测可以很好地弥补不同单模型预测所带来的局限性。

多模型的组合预测有着单模型不可比拟的优势。1963年，Barnard[2]首次提到模型合并；之后，Bates等[3]首次提出合并预测方法可以综合各单模型预测模型的有效信息，避免单模型在复杂情况下对现实结果预测的局限性；随后，合并预测受到越来越多学者的关注[4]，各种合并预测方法被学者提出，如最小方差合并预测方法[5]、贝叶斯统计方法[6-7]、变权重方法[8]等。1997年，Buckland[5]提出了最小方差法合并预测方法；2014年，Park等[6]提出贝叶斯统计方法量化模型形式不确定性和模型合并预测方法，使得合并预测方法在工程结构领域开始得到应用。

随着合并预测开始在工程上得到应用，探究组合模型响应的不确定性来源[9-10]，使合并预测有着更为稳健、可靠的预测结果，对合并预测的模型形式进行灵敏度分析显得尤为重要。目前，对参数灵敏度的研究较为成熟。全局灵敏度分析方法主要有基本效应法[11-12]、导数法[13-14]、方差灵敏度分析法[15-17]、矩独立灵敏度分析法[18-21]等。基本效应法最初是由Morris[11]提出，通过输入变量的变化对输出响应的平均影响，其计算量随着输入变量的维数增加而线性增加；导数法最初是由Sobol等[13]提出，通过模型输出响应对输入变量偏导数平方的期望来衡量输入变量的重要性，由于要求偏导数，故其对于非线性程度较高的模型计算效率低；方差灵敏度分析法最初也是由Saltelli等[15]提出的，通过输入变量对输出响应方差的影响程度来衡量输入变量的重要程度；由于方差只是一个统计特征，在很多情况下反映出的信息不全面，故Borgonovo[19]提出了矩独立灵敏度分析法，其通过输入变量对输出响应概率密度函数的影响来衡量輸入变量的重要度，后来Liu等[21]又提出了基于累计分布函数的矩独立指标，这是通过描述输入变量对输出响应的累积分布函数的影响来衡量输入变量的重要度。此外，灵敏度分析在航空领域也得到了应用，如可用于结构及气动的分析与设计中[22-24]。由上可以看出，对参数的灵敏度分析已经日趋完善，但是鲜有文献对模型形式不确定的灵敏度进行研究。

本文针对组合模型方法下的灵敏度问题，提出模型灵敏度指标及其分析求解方法。首先提出两种模型灵敏度指标：模型方差灵敏度及模型矩独立灵敏度。同时给出对应的分析方法。然后，以典型螺栓连接件的随机振动多模型合并预测为例，分析计算其中各个单模型的模型方差灵敏度指标和矩独立灵敏度指标，由灵敏度指标值可得出组合模型中相对重要的模型，为组合模型预测的进一步提升提供更多信息。

1模型合并中的模型灵敏度指标及其求解

1.1基于模型合并的预测

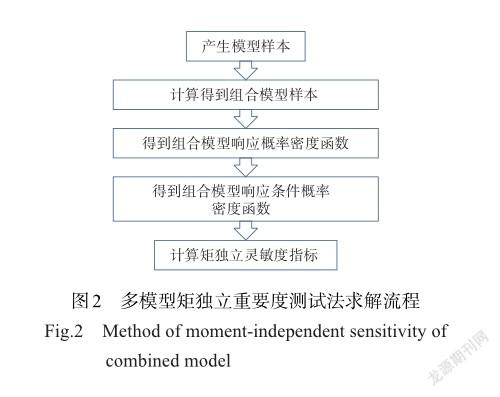
2实例：典型螺栓连接件的随机振动组合模型灵敏度分析

典型螺栓连接框架结构示意图如图3所示，该结构借鉴于参考文献[25]。针对螺栓连接不同的假设处理，分别建立了三个不同的框架结构有限元模型。如图4所示，其中图4（a）为h1板壳单元模型，该模型中将图3中的螺栓连接Bolt1～Bolt8都进行细化单独建模；图4（b）为h2实体单元模型，在该模型中连接Bolt7与Bolt8的不做细化建模；图4（c）为h3板梁单元模型，该模型中连接Bolt1～Bolt8均未细化建模，等效入上下横梁与侧柱的直接连接中去。本文的模型合并将在该三个模型的基础上进行。

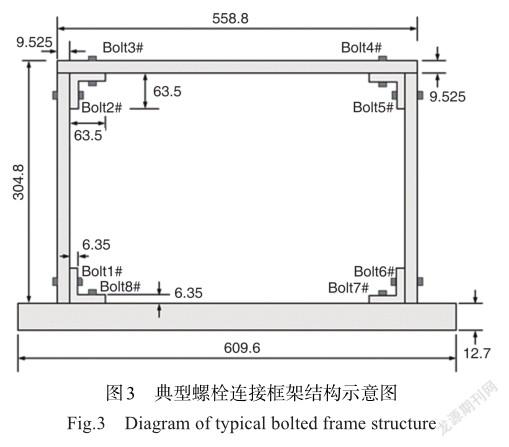
该结构中的随机变量包括E=[E1，E2，E3，E4，E5，E6，E7，E8，Eb，Ec]，其中Ei（i = 1，…，8）为第i个螺栓连接的弹性模量，Eb，Ec分别为上下横梁及两侧侧柱的弹性模量，还包括结构阻尼比ξ。各变量的分布信息见表1，其中正态分布的参数1和2分别为均值和标准差，均匀分布的参数1和2分别为上限和下限。

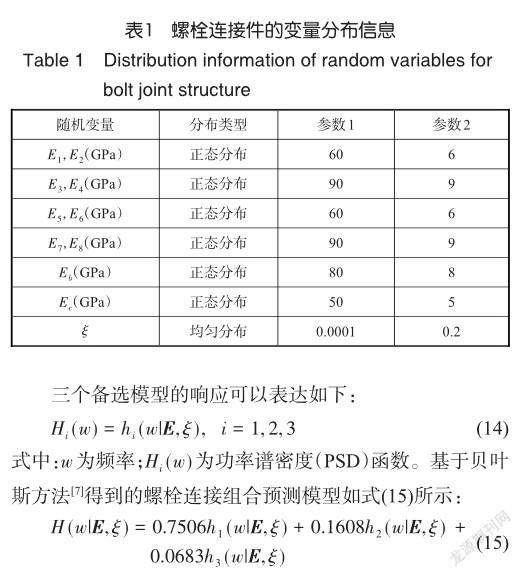
2.1固定频率点下的模型灵敏度分析

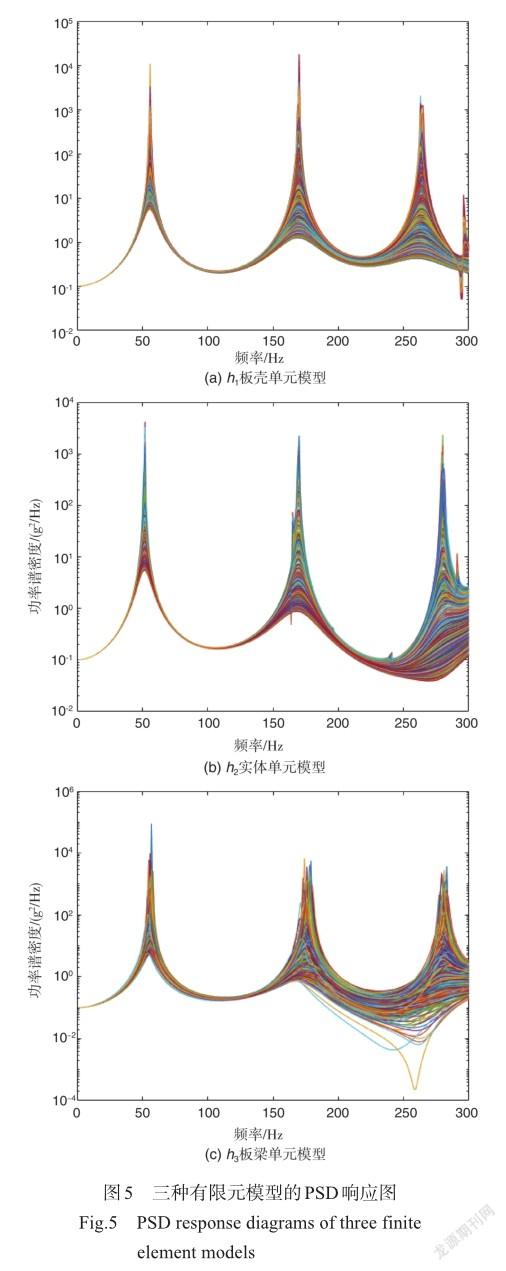
首先进行某一典型频率点下的灵敏度分析。依据模型中随机变量弹性模量和阻尼比的分布抽样N=1000组样本值，使用限元软件Nastran计算得到每一个模型在对应参数样本下的响应——功率谱密度（PSD）曲线，如图5所示。

鉴于162Hz为PSD响应图的第二个波峰附近，故先取各模型在固定频率点162Hz下的响应，求解各单模型在该处响应下的方差灵敏度和矩独立灵敏度指标，结果见表2。由表2可以看出，无论是矩独立灵敏度指标还是方差灵敏度指标上看，模型h1对于组合模型的影响是最大的。由结合式（15）可看出，模型h1的权重值是最大的，模型h2次之，模型h3最小。因此可以说明，权重值是影响组合模型灵敏度指标的一个因素，但灵敏度指标还受到模型中包含变量的影响，具体在下面的分析中体现出来。

2.2随机振动的模型灵敏度分析

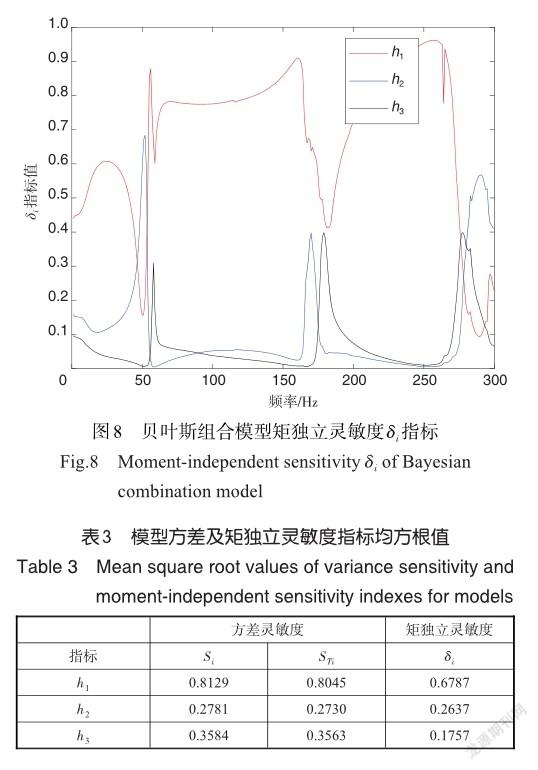
在2.1节中，只考虑了在某一固定频率点下的灵敏度分析，在这一节，将分析框架结构的随机振动功率谱密度（PSD）在各个频率下的灵敏度。随机振动的PSD为一曲线，这里对每一个频率点均进行灵敏度分析，最后得到方差和矩独立灵敏度指标随频率变化的结果，分别如图6～图8所示。从图6～图8中可看出，在大部分的频率点下模型h1对于组合模型的贡献度是最大的，这主要是由于模型h1的权重值是最大的。但是在有些频率点下出现交错现象，例如，图6中，在50～70Hz、160～180Hz和270～300Hz频率段，模型h3与模型h2的贡献度互相交错。这是由于在某些频率段下各模型输出响应的分布类型以及分布参数的不同。因此，影响模型灵敏度的指标因素为：一个是分配到每个模型的权重值，一个是模型本身的随机性（模型中的参数）。

为了更为直观地了解每一个模型的重要度，对灵敏度指标求其均方根值，得到如表3所示的数据。可以看出来，在贝叶斯方法下的组合模型，对组合模型的重要度排序为h1> h3> h2，且两种指标获得了一致的重要度排序结果。

3结论

本文分析探讨了以模型作为不确定性输入对组合模型输出响应方差以及概率密度函数的影响，类比随机变量灵敏度指标，提出了两种模型灵敏度指标。一是基于方差的模型灵敏度指标Si和STi，一是基于矩独立的模型灵敏度指标δi，来分别量化各单模型对组合模型的影响程度。

对航空典型螺栓连接件的随机振动组合模型进行了灵敏度分析，计算了不同的螺栓连接模型的方差灵敏度和矩独立灵敏度。从得到的指标值可以看出各模型在组合模型预测中的影响程度。从灵敏度函数结果看出，影响模型灵敏度的因素包括组合模型中各单模型的权重值和各单模型响应本身的不确定性（内部的不确定参数引起）。

參考文献

[1]Park I，Amarchinta H K，Grandhi R V. A Bayesian approach forquantificationofmodeluncertainty[J].Reliability Engineering System Safety，2010，95（7）：777-785.

[2]Barnard G A. New methods of quality control[J]. Journal of the Royal Statistical Society，1963，126（2）：255-258.

[3]Bates J M，Granger C W J. The combination of forecasts[J]. Journal of the Operational Research Society，1969，20（4）：451-468.

[4]Clemen R T. Combining forecasts：A review and annotated bibliography[J]. International Journal of Forecasting，1989，5（4）：559-583.

[5]Buckland S T. Model selection：An integral part of inference[J]. Biometrics，1997，53（2）：603-618.

[6]Park I，Grandhi R V. A Bayesian statistical method for quantifyingmodelformuncertaintyandtwomodel combination methods[J]. Reliability Engineering & System Safety，2014，129：46-56.

[7]袁修开，刘文杰.飞机结构疲劳可靠度贝叶斯组合预测[J].国防科技大学学报，2018，40（4）：100-105. Yuan Xiukai，Liu Wenjie. Bayesian combination forecasting for fatigue reliability of aircraft structures[J]. Journal of National University of Defense Technology，2018，40（4）：100-105. （in Chinese）

[8]袁修開，陈斌. Bootstrap与变权重相结合的多模型综合预测方法[J].机械科学与技术，2018（9）：1465-1471. Yuan Xiukai，Chen Bin.Multi-model comprehensive forecasting method combined with bootstrap and variable weight[J]. MechanicalScienceandTechnologyforAerospace Engineering，2018（9）：1465-1471. （in Chinese）

[9]肖思男，吕震宙，王薇.不确定性结构全局灵敏度分析方法概述[J].中国科学：物理学力学天文学，2018，48：014601. Xiao Sinan，Lyu Zhenzhou，Wang Wei. A review of global sensitivity analysis for uncertainty structure[J]. Scientia Sinica Physica， Mechanica，Astronomica，2018，48：014601 （in Chinese）

[10]吕震宙，李璐祎，宋述芳，等.不确定性结构系统的重要性分析理论与求解方法[M].北京：科学出版社，2015. Lyu Zhenzhou，Li Luyi，Song Shufang，et al. Importance analysis theory and solution method of uncertain structural system[M]. Beijing： Science Press，2015. （in Chinese）

[11]Morris M D. Factorial sampling plans for preliminary computational experiments[J]. Technometrics，1991，33（2）：161-174.

[12]Campolongo F，Cariboni J，Saltelli A. An effective screening design for sensitivity analysis of large models[J]. Environmental Modelling Software，2007，22（10）：1509-1518.

[13]Sobol I M，Kucherenko S. Derivative based global sensitivity measures and their link with global sensitivity indices[J]. Math Comp Simul，2009，79：3009-3017.

[14]Kucherenko S，Rodriguez-Fernandez M，Pantelides C，et al. Monte Carlo evaluation of derivative-based global sensitivity measures[J]. Reliability Eng Syst Safety，2009，94（7）：1135-1148.

[15]Saltelli A，Sobol I M. Sensitivity analysis for nonlinear mathematical models：numerical experience[J]. Institute for Mathematical Modelling，1995，7（11）：16-28.

[16]SobolIM.Globalsensitivityindicesfornonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation，2001，55（1-3）：271-280.

[17]Saltelli A，Annoni P，Azzini I，et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index[J]. Computer Physics Communications，2010，181（2）：259-270.

[18]Chun M H，Han S J，Tak N I. An uncertainty importance measure using a distance metric for the change in a cumulative distributionfunction[J].ReliabilityEngineeringSystem Safety，2000，70（3）：313-321.

[19]Borgonovo E. A new uncertainty importance measure[J]. Reliability Engineering and System Safety，2007，92（6）：771-784.

[20]Liu Q，Homma T. A new computational method of a momentindependent uncertainty importance measure[J]. Reliability Engineering and System Safety，2009，94（7）：1205-1211.

[21]Liu Q，Homma T. A new importance measure for sensitivity analysis[J]. Journal of Nuclear Science and Technology，2010，47（1）：53-61.

[22]尹俊杰，常飛，李曙林，等.基于Sobol法的整体翼梁损伤容限设计参数灵敏度分析[J].空军工程大学学报（自然科学版），2013， 21（6）： 9-12. Yin Junjie， Chang Fei， Li Shulin， et al. Analysis of parameter sensitivity on damage tolerance design of overall beam based on Sobol method[J]. Journal of Air Force Engineering University （Natural Science Edition）， 2013， 21（6）： 9-12.（in Chinese）

[23]夏露，杨梅花，李朗，等.基于全局灵敏度分析方法的气动设计研究[J].西北工业大学学报，2018， 36（1）： 49-56. Xia Lu， Yang Meihua， Li Lang， et al. Aerodynamic design based on global sensitivity analysis method[J]. Journal of Northwestern Polytechnical University， 2018， 36（1）： 49-56.（in Chinese）

[24]毕富国，何广平.微型扑翼飞行器动力学模型参数的灵敏度分析[J].兵器装备工程学报，2019，40（8）： 94-99. Bi Fuguo， He Guangping. Sensitivity analysis of dynamic model parameters of flapping-wing micro air vehicles[J]. Journal of Ordnance Equipment Engineering， 2019， 40（8）： 94-99.（in Chinese）

[25]Van Buren K L，Hall T M，Gonzales L M，et al. A case study toquantifypredictionboundscausedbymodel-form uncertainty of a portal frame[J]. Mechanical Systems and Signal Processing，2015，50：11-26.

Sensitivity Analysis of Multiply Random Vibration Models for Typical Bolt Connection

Yuan Xiukai，Zhao Chaofan，Zheng Zhenxuan，Kong Chongchong Xiamen University，Xiamen 361005，China

Abstract： In order to analyze the sources and impacts of uncertainties on combined model output， the variance sensitivity and moment-independent sensitivity for the combined models are proposed； also， the sensitivity analysis methods are presented. Model variance sensitivity is to quantify the influence of each model on the variance of the combined model output response. Model moment-independent sensitivity is to quantify the influence of each model on the probability density function of the combined model output response. Finally， based on a typical bolt connection combination forecast， the model sensitivity of structural random vibration combination forecast model is analyzed. The result shows that two factors affect the model sensitivity： the weight value of the combined model and the uncertainty of every single model itself （caused by internal parameters）.

Key Words： sensitivity analysis； combined model； uncertainty； random vibration

3816500338202