不同正中矢状面在面部对称性评价中的应用效果比较

邓艾佳，刘义闻，吴坡，李浩，张正瑞，，羊书勇

1西南医科大学口腔医学院，四川泸州 646000；2空军军医大学第三附属医院口腔颌面外科；3西部战区总医院口腔科

面部对称性是人体面部美学评价指标之一［1］，也是外科医生美学修复及面部重建的基本目标之一［2］。基于标准正中矢状面（MSP）建立的三维镜像模型，可以极大程度恢复及重建目标区域的正常形态［3-4］，对外科手术恢复颌面部原始外形有重要的参考价值。然而人体颌面部发育受生物因素、环境因素等多重影响，并不存在理论上的完全对称，且研究发现面部不对称性的发展具有无法预测性［5-6］，这也使得目前MSP的建立尚无公认的标准流程或特定方式。目前，通过头颅解剖标志点定位MSP是临床最常用的方式［7］。基于激光扫描仪采集的面部图像、3D重建图像或计算机断层扫描图像等多种立体三维成像方式［8-10］，选取头颅中线平面的解剖标志点可快速建立MSP。然而，有研究提出多个可作为定位MSP的理想头颅解剖点，尚未有足够统计学资料提出可应用于临床的标准MSP。本研究基于三个常用的MSP［11-13］，选择30例颌骨发育正常的患者，采集患者的螺旋CT数据导入Mimics软件重建三维头颅模型，以相应MSP作为对称面进行镜像操作，通过3-Matic Research软件进行热图对比，计算镜像后模型与原模型重叠参数，以选择颅颌面理想的对称平面。

1 资料与方法

1.1 临床资料 选择2020年6—12月就诊于西部战区总医院颌面外科并确诊为下颌下腺良性疾病的患者30例，颌骨形态功能均正常，男15例、女15例，年龄20～60岁。纳入标准：①均符合下颌下腺良性疾病的诊断标准。②年龄20～60岁。③无颅颌面发育畸形。④无颌面部外伤史或手术治疗史。⑤影像资料（螺旋CT）清晰完整。⑥颌面部满足基本对称要求条件：三维头颅上下颌骨均各选取两组对称点（上颌骨：眶外侧点、眶下孔；下颌骨：髁突外侧最凸点、颏孔点），面部双侧解剖标志点与颏前点的距离差距均不超过3 mm。本研究已通过西部战区总医院伦理委员会审批（2021ky134-1）。

1.2 方法

1.2.1 构建三维模型 采集30例患者的64排颌面部螺旋CT影像资料，以DICOM格式文件保存并导入Mimics Research 21.0，采用合适阈值（400～3 071 Hu）建立颅骨蒙版，重建三维头颅模型。

1.2.2 MSP建立 结合三维图像矢状面、冠状面、横截面定位解剖标志点，建立3种MSP，分别为由鼻根点—前鼻棘点—后鼻棘点构成的平面（N-ANSPNS）、由鼻根点—前鼻棘点—蝶鞍点构成的平面（N-ANS-S）、由鼻根点—颅底点—蝶鞍点构成的平面（N-Ba-S）。由1名高年资医师分不同时间点进行2次定位，取2次定位的中点为最终标志点以减小随机误差。

1.2.3 各解剖点的定位 蝶鞍点（S）：蝶鞍影像的中心；鼻根点（N）：鼻额缝的最前点；前鼻棘点（ANS）：前鼻棘之尖；后鼻棘点（PNS）：硬腭后部骨棘之尖；颅底点（Ba）：枕骨大孔前缘之中点。见图1。

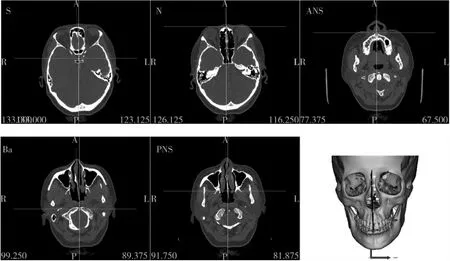
图1 各解剖标志点在Mimics软件窗口的定位

1.2.4 镜像 Mimics Research 21.0软件中执行“3D TOOLS-Mirror”，以原模型为目标，分别以N-ANS-PNS、N-ANS-S、N-Ba-S作为镜像平面，点击“OK”，自动生成3组镜像后模型。

1.2.5 原模型及镜像后模型对比 将三维重建原模型与镜像后模型以“STL”文件格式导入3-Matic Research 13.0比较分析，将三维重建原模型设置为“Entity”，镜像后模型设置为“Target Entity”，执行“Analyze-Creat a Part Comparison Analysis”。软件以原模型及镜像后模型的对应点为单位对比两者重叠度差异，自动计算各镜像后模型与原模型的重叠度差异（平均点距差异）及标准差范围，颜色不同则显示不同位置点的影像存在差异。均设置相同Histogram range范围（-2.000～4.000 mm），绿色区域代表镜像后模型与原模型重叠部分，即数值越接近“0”，两者匹配度越高；红色区域代表凹陷的部分（镜像模型表面凹陷于原模型表面），正数值越大，颜色越深，代表镜像后模型与原模型平均重叠度差距越大，即镜像后模型与原模型匹配度越低；蓝色区域代表突出部分（镜像模型表面突出于原模型表面），负数值越大，颜色越深，即与原模型差距越大，即镜像后模型与原模型匹配度越低。

1.3 统计学方法 采用SPSS23.0统计软件。非正态分布的计量资料以中位数及四分位数间距表示［M（P25，P75）］，组间比较采用Friedman秩和检验。P＜0.05为差异有统计学意义。

2 结果

以N-ANS-PNS、N-ANS-S、N-Ba-S为镜面平面的镜像模型与原模型之间的重叠度差异分别为0.33（0.22，0.50）、0.41（0.26，0.74）、0.79（0.31，1.61）mm，三者数据离散性分别为0.06～0.72 mm、0.08～1.23 mm、0.13～3.34 mm。平面N-ANS-PNS、N-ANS-S重叠度差异低于平面N-Ba-S（P均＜0.05）；平面N-ANS-PNS与平面N-ANS-S重叠度比较差异无统计学差意义（P均＞0.05），但平面N-ANS-PNS离散性低。

3 讨论

术前准确评估及定量患者的面部情况、预测术后患者面部形态变化、制定精准的手术计划在颌面部重建过程中不可或缺［14-15］。面部对称性的评估通常需要使用特定的测量方式，常用的方法主要包括直接人体测量、传统二维头影测量、三维立体摄影测量、彩色3D扫描、计算机断层扫面成像等。通过三维摄影测量研究发现，颌面部最大不对称区域发生于面上部1/3者约占10%，发生于面中部1/3者约占49%，41%则分布于面下部1/3［8］。面部不对称性主要原因是由于下颌骨双侧不对称，同时通过三维成像镜像技术评估了面部对称性，结果表示通过二维或三维图像多个对称标志点评估颌面部的不对称性，往往局限于有限区域的差异，而无法评估三维整体形态的差异［16］。镜像技术则通过直观可视的方式直接反映三维图像的重叠区域及非重叠区域，通过图像的色彩、多个比较参数直接体现图像的相似性指数差异。在面部对称性评估过程中，精确的对称平面是评估面部对称性的重要定量工具，也是外科治疗中缺损重建及恢复单侧骨折的重要辅助手段，对于患者特异性植入物设计和正颌手术计划也必不可少［17-18］。然而，颌面部并不存在理论上的完全对称，且颌面部发育模式存在群体不一致性及无序性，这使得颌面部对称性评估充满挑战。

对于颌骨单侧病损的重建手术治疗方式主要包括游离自体骨移植、带血管蒂自体骨移植、异体骨移植以及钛板钛钉植入，也有学者提出3D植入物的应用［19-20］。随着患者对治疗效果及面部美学要求的提高，数字化治疗技术成为目前治疗下颌骨病变的重要辅助手段，大量研究证明了数字化技术的优势［21］。在颌面部病变数字化治疗过程中，确立面部正中矢状平面，并基于此平面行头颅模型”镜像”操作是必不可少的部分，也是决定治疗效果的关键步骤。

随着三维技术的普及，通过立体成像技术进行对称性分析为寻找到最佳MSP提供了更精确的解剖指标。本研究则选取最常用的三个MSP应用于临床分析，将三维原模型和镜像后模型重叠后的热图进行对比，以立体成像的每个点为单位作对比分析，计算模型总体平均重叠度差异，经可视化颜色及自动计算差值直观反映对称平面的合理性及准确性。结果发现N-ANS-PNS平面、N-ANS-S平面及NBa-S平面三个MSP间差异有统计学意义，且统计发现N-ANS-PNS平面构建的镜像后模型与原模型的差异小且数据离散度低，尤其是在正面视角的面前区域，在热图分析中，色彩显示为绿色区域分布面积最大，反映出两模型在额骨、颧骨前部、上颌骨、下颌体等部位匹配度最高，而在双侧下颌升支及髁突部位的匹配度欠佳，结合平均重叠度差异结果可以得出结论，即研究结果支持N-ANS-PNS平面作为相对理想的MSP，N-ANS-S平面体现颌面部对称性的效果较次，以N-Ba-S作为MSP应用效果不佳，同时本研究结果也证明后鼻棘点（PNS）较蝶鞍点（S）应用效果相对更加稳定，前鼻棘点（ANS）较颅底点（Ba）更靠近真实面部MSP。

因此本研究建议在临床应用MSP恢复或重建患者额骨、颧骨前部、上颌骨、下颌体等部位的颌面部缺损区域骨骼时，可以优先选择平面N-ANS-PNS作为镜像对称面，从而快捷、准确地达到最终预期效果。但对于颌面部软组织缺损严重的患者，由于通过颌面部螺旋CT数据所重建的软组织模型与真实体貌存在一定差异，对于精细部位的重建，如瞳孔、眉部等部位尚不如有学者所提出的面部光学扫描图像等直观图像，因此颌面部软组织的正中矢状平面分析还需进一步研究。

综上所述，MSP的确立在面部对称性评估中十分关键，理想的MSP有重要临床价值。本研究认为不同面部中线标志解剖点所产生的MSP存在差异，在进行颌面部骨骼数字化重建时，对于额骨、颧骨前部、上颌骨、下颌体等颌面部骨骼病变部位的患者，本研究认为N-ANS-PNS平面可以作为相对理想的MSP，结合三维重建及镜像技术，将有效帮助外科医生完成骨骼重建、正颌手术等临床工作，同时提高颌面外科临床治疗的有效性及可靠性。