基于非约束模态的中心刚体-Timoshenko梁动力学建模与分析*

关玉铭， 戈新生

（北京信息科技大学 机电工程学院，北京 100192）

引 言

对于航空发动机，叶片是其至关重要的组成部分，其性能直接决定发动机可能达到的最高转速.对于这种结构，一般将其视作高速旋转运动的中心刚体-挠性梁结构.目前，对中心刚体-挠性梁结构的研究大多为Euler-Bernoulli 梁[1-2].Euler-Bernoulli 梁多为细长梁，其力学特性忽略了剪切变形以及剪切变形对转动惯量的影响，因此不少学者对考虑了剪切变形影响的Timoshenko 梁进行了大量研究[3-5].1987 年，Kane 等[6]通过对旋转的悬臂梁实验提出了“动力刚化”这一概念，动力刚化即模型的广义刚度随转速的提高而增大的现象，对于这种现象，国内外许多学者对其进行了深入研究.方建士、章定国等[7-9]对旋转的悬臂梁进行了研究，在考虑横向变形引起纵向变形的二次耦合项的前提下，应用Hamilton 原理和假设模态法推导出了带动力刚化项的一次近似耦合模型.杨辉、洪嘉振等[10-12]验证了在高速旋转情况下，采用零次模型计算梁的横向振动响应时会产生错误的结论.针对“中心刚体-柔性梁结构”这种刚柔耦合模型的动力学特性，蔡国平、洪嘉振做了充分的研究[13-14].而对于Timoshenko 梁的动力刚化现象研究较少，Hao 等[15]通过Hamilton 变分原理建立了双向功能梯度Timoshenko 梁动力学模型并采用传统方法推导出了动力刚化矩阵，Banerjee[16]建立了含有离心力的Timoshenko 梁动力学模型，并推导了动力刚度矩阵.You 等[17]运用Hamilton 原理建立了考虑剪切变形的柔性梁动力学模型，并通过有限元方法进行离散，探究了Timoshenko 梁的动力学特性.对于传统Timoshenko 梁，因没有考虑剪切变形所产生的角加速度，导致消去转角位移后所得到的四阶微分方程中含有挠度对时间的四阶偏导数项，因该项的存在导致出现两个固有频率.因此，陈镕等[18-19]考虑了剪切对转动惯量的影响，导出了修正的Timoshenko 梁动力学模型，并对修正Timoshenko 梁的动力学特性进行了分析，给出梁模型仅对应一个固有频率.陕晋军等[20]对非约束模态和约束模态的求解方法进行了研究，并对二者频率进行了定量分析，得出挠/刚惯量比大小对固有频率影响较大，因此当挠/刚惯量比较大时要想得到较为准确的固有频率，采用非约束模态进行求解更为准确.Low 等[21]通过实验方法得出非约束模态建模方法优于约束模态.Xiao 等[22]针对离心力对悬臂梁结构广义刚度的影响进行了探究，得出离心张力会引起系统刚度增加，离心压缩力会引起系统刚度减小.Timoshenko 梁是在Euler 梁的基础上考虑剪切的影响，为Euler 梁的一种复杂情况，因此理论上离心力应对其存在同样的效应.本文以中心刚体-Timoshenko 梁为力学模型，建模过程中考虑梁上所受离心张力，并求解其约束模态振型函数和固有频率以及非约束模态振型函数和固有频率，最后给定转动规律，通过数值仿真对两种模态下模型的广义刚度和梁末端响应进行分析.

1 系统动力学方程

首先，将航空发动机近似视作中心刚体-挠性梁系统，以Timoshenko 梁为研究对象，如图1 所示.考虑粗短梁，其变形二次耦合项较小，可假设为零.以中心刚体质心O为原点建立惯性坐标系XOY，中心刚体与梁连接点为Oc，并以Oc为原点建立连体坐标系XcOcYc，a为中心刚体半径.取梁上微元质量dm为研究对象，点P为微元质量质心，Ux(x,y,t) 为 梁的轴向变形，Uy(x,y,t)为 梁的横向变形.微元质量dm变形如图2 所示， θ(x,t)为截面转角，γ(x,t)为剪切角，Q和M分别表示微元质量所受剪力和变矩， θ (0,t)为中心刚体与梁连接处转动角度同时也表征中心刚体的转动角度.为点P′在惯性坐标系下的位置矢量.根据非线性变形理论可得

图1 中心刚体-Timoshenko 梁系统结构图Fig.1 The structural diagram for the central rigid body-Timoshenko beam system

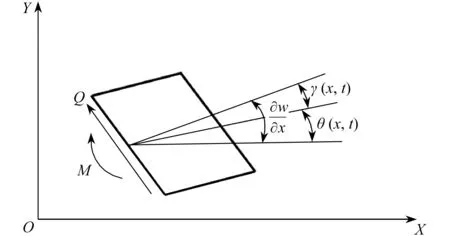
图2 梁上微元质量变形Fig.2 The mass deformation of an infinite simal element on the beam

其中，v(x,t) 为 轴向变形，γ (x,t) 为 剪切角，w(x,t)为 挠度.梁变形后点P′的坐标为

将其投影到惯性坐标系下为

考虑离心力产生的轴向变形对模型广义刚度的影响，因此假设v(x,t)=0,微元质量在惯性坐标系下沿X，Y方向的速度分别为

式中 ()′表示对变量x求一阶偏导数,单下划线部分为引入离心力的产生项， ρ为 线密度， κ为剪切系数[24]，对于矩形截面，I为截面惯性矩.当为自由振动时，q(x,t)=0，式（15）为

2 基于非约束模态的离散动力学方程

设梁的横向振动变形为

3 非约束模态动力学方程特征问题求解

假设梁挠性振动和转角模态展开为

其中φ (x)，Θ (x)为 振型函数， ω为 频率.将式（25）代入式（20）可得振型函数φ (x)的偏微分方程.

对于非约束模态，其边界条件为

将非约束模态边界条件代入式（31）、（32）可求得系数A1～A4，C1～C4， 非约束模态振型函数φ (x)以及非约束模态固有频率.

4 数值仿真

为研究转速对广义刚度及响应的影响，给出模型在不同恒定转速的仿真结果.转动规律为

T为姿态机动时间，T= 100 s， Ω0为恒定转速.Timoshenko 梁参数如表1 所示.

表1 Timoshenko 梁参数Table 1 Parameters of the Timoshenko beam

根据第3 节求得的频率方程，进一步求解得到非约束模态柔性结构前二阶固有频率为ω1=0．623 5 rad/s, ω2=1．689 2 rad/s.因柔性结构第一阶固有频率较为重要，本节给出动力学模型在约束模态与非约束模态情况下，K取第一阶固有频率时，广义刚度随 转速的关系，如图3～6 所示，此时恒定转速 Ω0分别取0.1 rad/s，0.5 rad/s，1 rad/s，5 rad/s.

图3 恒定转速为0.1 rad/s 的广义刚度Fig.3 The generalized stiffness at a constant speed of 0.1 rad /s

图4 恒定转速为0.5 rad/s 的广义刚度Fig.4 The generalized stiffness at a constant speed of 0.5 rad /s

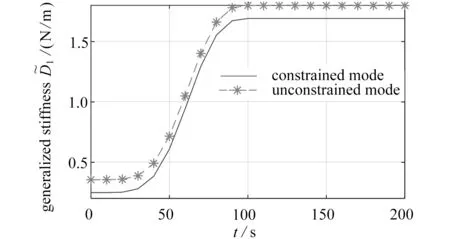
图5 恒定转速为1 rad/s 的广义刚度Fig.5 The generalized stiffness at a constant speed of 1 rad /s

图6 恒定转速为5 rad/s 的广义刚度Fig.6 The generalized stiffness at a constant speed of 5 rad /s

图7 恒定转速为0.1 rad/s 的广义刚度Fig.7 The generalized stiffness at a constant speed of 0.1 rad /s

图8 恒定转速为0.5 rad/s 的广义刚度Fig.8 The generalized stiffness at a constant speed of 0.5 rad / s

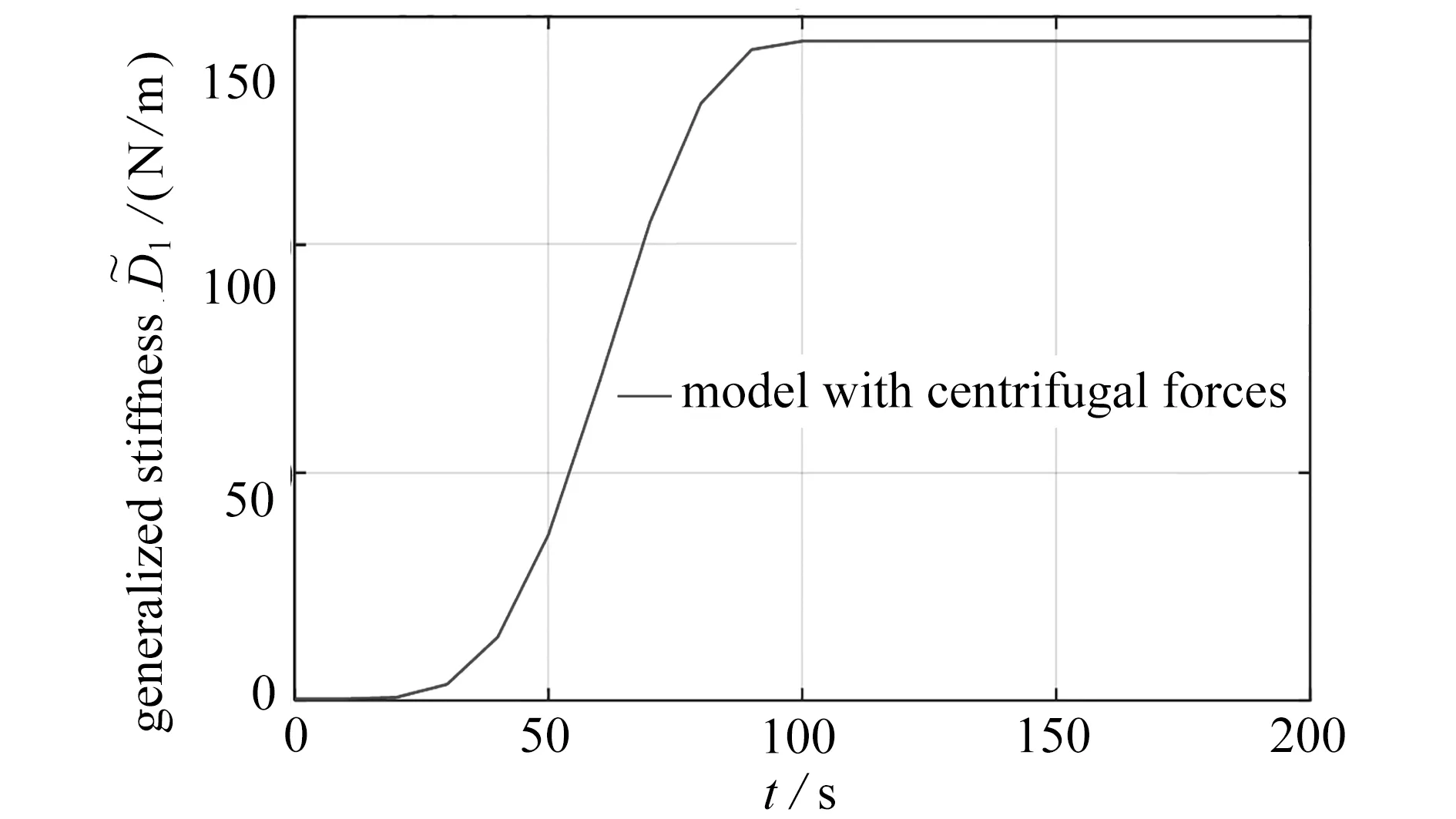
图9 恒定转速为10 rad/s 含离心力模型的广义刚度Fig.9 The generalized stiffness of the model with centrifugal forces at a constant speed of 10 rad / s

从图11 可以看出，当转速很低时，两曲线几乎重合，模型是否包含离心力F(x)，对梁末端响应影响较小.当转速增大至Ω0=0．5 rad/s 接 近一阶固有频率 ω1时，离心力对梁末端响应的影响开始明显，不含离心力模型的响应振幅与含离心力模型偏差较大，如图12 所示.当转速提升至 Ω0=10 rad/s时不含离心力模型响应发散，与图10 广义刚度曲线小于零的情况相对应，模型失效，此时含离心力模型响应依然收敛，存在动力刚化现象，如图13 所示.

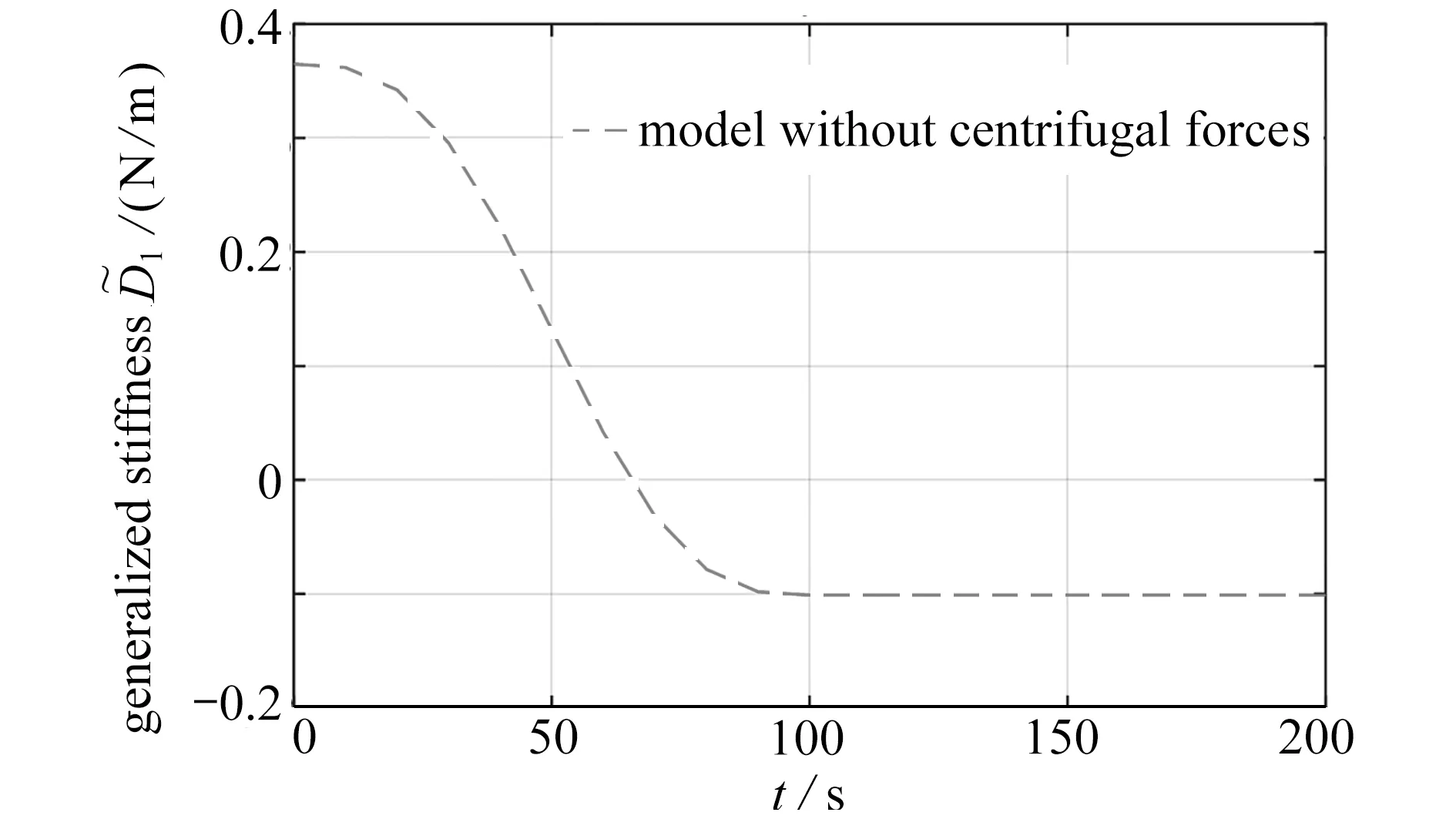
图10 恒定转速为10 rad/s 不含离心力模型的广义刚度Fig.10 The generalized stiffness of the model without centrifugal forces at a constant speed of 10 rad / s

图11 恒定转速为0.1 rad/s 时，梁末端振动响应Fig.11 Vibration responses of the beam end at a constant speed of 0.1 rad / s

图12 恒定转速为0.5 rad/s 时，梁末端振动响应Fig.12 Vibration responses of the beam end at a constant speed of 0.5 rad / s

图13 恒定转速为10 rad/s 时，梁末端振动响应Fig.13 Vibration responses of the beam end at a constant speed of 10 rad / s

5 结 论

本文以中心刚体-Timoshenko 梁系统为力学模型，考虑非约束模态与约束模态的差异，探究此时离心力对模型的广义刚度和振动响应的影响，得出如下结论：

1） 低转速时，非约束模态与约束模态模型的广义刚度偏差较大，高转速时，由于离心力的影响，非约束模态与约束模态模型的广义刚度偏差较小.

2） 非约束模态条件下，离心力对中心刚体-Timoshenko 梁模型的广义刚度影响较大，随着转速的提升，广义刚度不断增大，存在动力刚化现象.

3） 如果不考虑离心力以及变形二次项，高转速时中心刚体-Timoshenko 梁模型会出现广义刚度为负的现象，且此时求得的振动响应发散，因此中心刚体-Timoshenko 梁模型建模过程中，应充分考虑离心力的影响.