离散动力系统1∶2共振情形下的余维二分岔反控制*

杨宇娇， 徐慧东， 张建文

（1.太原理工大学 数学学院，太原 030024；2.太原理工大学 机械与运载工程学院，太原 030024）

引 言

分岔是由非线性动力系统的参数发生变化所引起的，系统拓扑结构变化的一种非线性现象.相较于连续系统中较为完备的分岔理论，离散系统(映射)中也蕴含着丰富的动力学.许多学者研究了离散动力系统下复杂的分岔行为，并且取得了不少有价值的研究成果[1-8].Pecora[6]基于一个二维离散时间垄断模型定性分析了在1∶4 共振点附近出现的分岔序列，发现了许多复杂的动力学现象.Ren 等[7]基于一个离散时间信息扩散模型，讨论了由Neimark-Sacker 分岔退化引起的1∶2 共振、1∶3 共振和1∶4 共振.Li 等[8]基于一个离散Hindmarsh-Rose 模型，用内积法和规范形理论分析了flip 分岔、Neimark-Sacker 分岔以及1∶2 共振分岔，并给出了1∶2共振发生的条件.

分岔控制指的是通过控制改变原非线性系统的特性进而来获得所需要的动力学行为.早期分岔控制的研究包括延迟固有分岔的发生以及稳定现有的分岔，但随着对分岔机理的深入研究和非线性控制理论的发展，Chen 等[9]开创性地研究了washout-filter 反馈控制器下连续系统Hopf 分岔反控制问题.自此，有不少学者开始对分岔反控制问题进行研究[10-16].需要强调的是，分岔反控制是传统分岔控制的逆问题，其任务就是通过控制在系统预先指定的系统参数点设计出具有所期望特性的分岔.Wen 等[14]提出了一种新的反馈控制方法，并基于此方法实现了共振情况下的Hopf 分岔.伍新等[15]使用线性反馈控制方法研究了一类含间隙的三自由度高维碰撞振动系统的Neimark-Sacker 分岔反控制问题.徐慧东等[16]对一类含间隙碰撞振动系统Poincaré映射的Hopf-Hopf 交互分岔进行了反控制研究.

值得注意的是，在实施分岔的反控制时，需要按分岔的临界准则反求出控制增益参数，进而通过调控增益参数来生成所期望的分岔解.而传统的分岔准则是用特征值的特性来描述的，对于低维系统，由于其线性化矩阵的特征值具有解析的表达式，所以基于传统的分岔准则来确定分岔存在是有效的.但对于高维系统，由于其线性化矩阵的特征值一般无法解析表示，这样基于传统的分岔准则来研究分岔的存在性，通常需要逐点取值去检验在某个参数点分岔的存在性，具有一定的局限性.针对这个局限性，Wen[17]提出了任意维映射的，不依赖于特征值计算的Hopf 分岔显式临界准则.随后，有不少研究者对其他分岔的显示准则问题进行了研究.Xu 等[18]提出了一种新的准则来研究继电器反馈系统极限环的叉式分岔问题，并利用数值模拟验证了新准则的准确性.Yao[19]针对一般意义下的离散系统的余维二分岔，提出了一种新的flip-Neimark-Sacker 分岔临界判据.据笔者所知，目前有关高维映射的1∶2 共振情形下的余维二分岔反控制的问题，尚未有报道.

本文发展了一种控制方法，基于该方法对三维映射的1∶2 共振分岔进行了反控制研究.针对传统的映射1∶2 共振分岔准则在确定分岔点存在的局限性，建立了不直接依赖于特征值计算的显式临界准则，并基于显式准则，通过设计线性控制增益来确保系统会发生1∶2 共振分岔.然后，应用中心流形-范式方法进一步通过确定非线性控制增益分析了1∶2 共振分岔解及其稳定性.最后，针对一个三维的Arneodo-Coullet-Tresser 映射，通过设计线性和非线性控制增益在指定的参数点处实现了1∶2 共振分岔的各种分岔解.

1 控制系统

考虑一个一般的三维离散动力系统：

其中µ ∈R2是 分岔参数，函数f1，f2，f3关 于x,y,z和µ 是充分光滑的.

本文的目的是通过设计一个适当的控制器，在预先指定的位置µ =µ0处，使系统(1)产生1∶2 共振情形下的余维二分岔.设计一个离散时间的滤波反馈控制器并施加到原系统(1)，可得如下的控制系统：

其中X=(x,y,z,w)T， µ ∈R2，w为滤波器状态变量，为滤波器输出函数.当=0时 ，u(s)=0,v(s)=0，这样滤波器在控制过程中会保持原系统(1) 的不动点.对于一个稳定的滤波器，r在 ( 0,2)范 围内变化，并且r的选取会影响控制的收敛速度.控制增益矩阵K由控制器的系数kij(i=1,2,3，j=1,2 ) 构成，其中的线性控制增益k11，k12被用于控制1∶2 共振情形下的余维二分岔的发生，非线性控制增益k21，k31，k22，k32能够灵活地操纵所发生的1∶2 共振分岔，确定该分岔所产生的分岔解的类型和稳定性，从而实现一些理想的动力学行为.在下一节中，我们将发展一些适当的公式来确定这些增益.

2 线性控制增益的设计

控制系统(2)～(4)在不动点x∗(x0,y0,z0,w0)处的Jacobi 矩阵为

传统的映射1∶2 共振的临界分岔条件表述如下.

命题1[20]当控制系统(2)～(4)满足如下的条件(C1)和(C2)：

(C1) 特征值分布条件 在 µ =µ0处，Jacobi 矩阵(5)有两个实特征值λ1(µ0,KL)=λ2(µ0,KL)=−1，其余特征值λi(µ,KL),i=3,4 在单位圆内，即| λi(µ0,KL)|<1；

系统将在µ =µ0处发生1∶2 共振分岔.

命题1 中条件(C1)和(C2)是1∶2 共振情形下的余维二分岔的重要临界条件，决定了映射中是否存在该分岔.显然，该命题是用特征值的性质表示的，也就是说分析分岔的存在与否，需要借助特征值的解析表达式或在参数空间中通过数值搜索方法寻找分岔点.由于Jacobi 矩阵(5)是一个高阶矩阵，且包含了一些需要被确定的控制参数k11和k12，所以通过求解特征值的解析表达式来确定这些控制参数是很困难的.为了更方便、有效地根据临界分岔条件得到线性增益KL，进而分析1∶2 共振情形下的余维二分岔的存在性，下文将给出四维离散动力系统1∶2 共振情形下的余维二分岔的显式判据.该判据是由特征多项式方程的系数所组成的一组等式或不等式构成的，与特征值的计算无关.

在建立新的显式临界判据之前，先给出映射(2)的Jacobi 矩阵(5)在不动点x∗处的特征多项式为

其中a0=1， 并且aj=aj(µ,KL),j=1,2,3,4.再定义如下行列式序列：

通过使用多项式(6)与行列式(7), 可以得到如下命题.

命题2映射(2)在µ =µ0处发生1∶2 共振的必要不充分条件为(H1)与(H2)：

(H1) 特征值分布条件

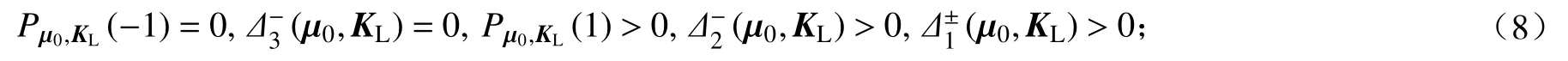
(H2) 横截条件

其中表示ai(µ,KL)关 于µ 在 µ =µ0处 的导数，i=1,2,3,4.

为了证明所提出的显式临界准则的必要性，需要先引入下述引理.

引理1[21]针对三次多项式方程0 有一个实特征根−1，其余的所有特征根都在单位圆内的充分必要条件由下述条件(M1) 与(M2)给出：

(M1) 特征值分布条件

(M2) 横截条件

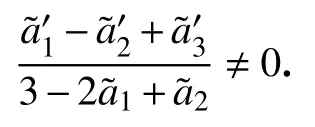
证明如果条件(C1)与(C2)可以推得条件(H1) 与(H2), 那么命题2 就构成了映射发生1∶2 共振的一个必要条件.

首先证明条件(H1)的必要性，假设条件(C1)成立，根据λ1(µ0,KL)=−1， 必有条件(H1)中Pµ0,KL(−1)=0成立.在确保有特征值−1 的情况下，在µ =µ0处特征多项式(6)可写为如下形式：

其中

根据命题1 和引理1, 条件(C1)中的 λ2(µ0,KL)=−1， |λi(µ,KL)|<1，i=3,4表明条件(M1) 成立.展开等式(10)的右侧，并同等式(6)的系数作比较可得

根据如下公式[22]：

以及式(10)、(13)、条件(M1)，很容易证明条件(H1)中

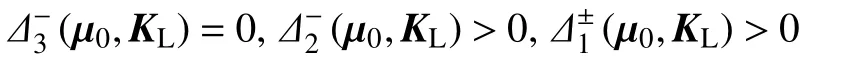
成立.故条件(H1)的必要性得证.

接下来说明条件(H1)的不充分性，假设条件(H1)成立，则必然成立，已知[23]

也必然成立，命题2 得证.

在本节中，利用命题2 通过调节线性控制增益k11和k12，可以保证系统(2)～(4)产生1∶2 共振分岔.从命题2 的条件(H1)和(H2)可以看出，这些不等式可以快速排除一些参数区域并直接确定临界分岔的控制参数区域，从而避免了对关键参数点费力的数值搜索，简化了繁重的计算.与传统临界判据相比，本文提出的临界判据更适合高维控制系统，可以更方便、有效地实现分岔点的确定.

3 非线性控制增益的设计

本节将基于中心流形-范式方法和1∶2 共振分岔理论，通过设计四个非线性控制增益k21，k31，k22，k32来分析1∶2 共振情形下的余维二分岔所产生的分岔解的稳定性和类型，实现一些理想的动力学行为.

命题3对于四维映射(2), 若其线性化矩阵(5)有两个特征值−1，其余都在单位圆内，则存在一个中心流形，可以将原映射降阶成与其局部动力学行为等价的二维映射.

证明做如下坐标变换，将不动点x∗和分岔点移至坐标原点处：

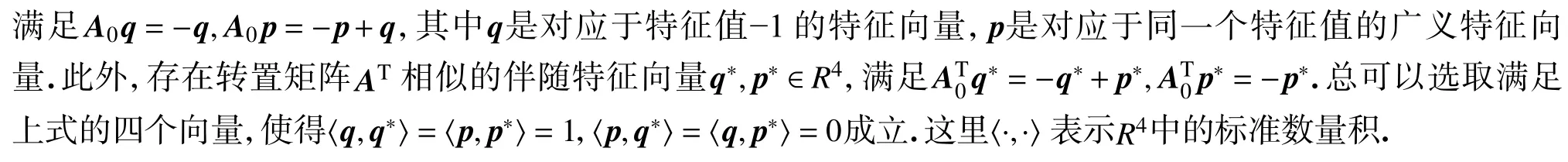
对于映射(16), 存在一个二维的中心流形如下：

该中心流形取决于参数 β=(β1,β2)，其中

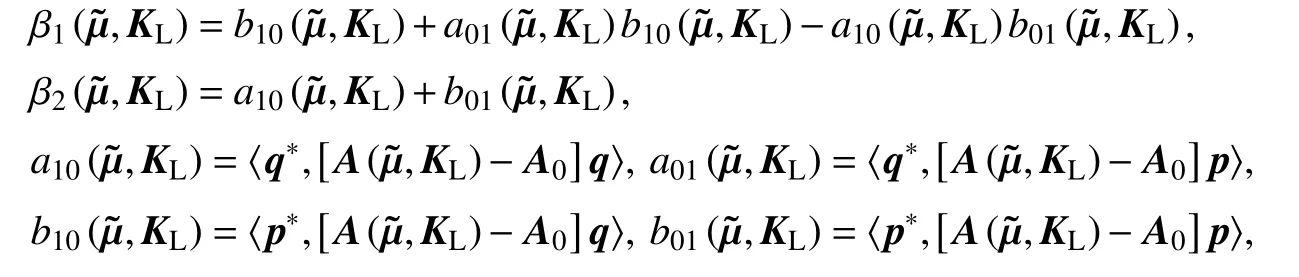
展开H有

以往对高维映射分岔的研究是通过中心流形将高维映射降阶成相应分岔的低维映射，然后再基于降阶后的映射导出范式.这里依据文献[24]的方法，直接通过推导中心流形将原映射降阶为1∶2 共振的范式映射.利用中心流形(17)可将式(16)降阶为如下的二维映射：

命题3 得证.

综上所述，映射(16)可以降阶为规范形(19), 且规范形系数可由式(22)、(23)求得，将规范形映射(19) 记为ωΓβ(ω).接下来，为了通过控制设计范式映射(19)的1∶2 共振的相应分岔解，需要用光滑流形近似这个映射.但由于映射(19) 的线性部分有负特征值，所以选择该映射的二次迭代来近似.

F(1)={(β1,β2):β1+O(‖β‖2)=0};

1) 仍存在pitchfork 分岔曲线

2) 存在非退化的Hopf 分岔曲线

H(1)={(β1,β2):β2+β1+O(‖β‖2)=0,β1<0},

H(2)={(β1,β2):C1(0,KNL)β2+C1(0,KNL)β1+2D1(0,KNL)β1+O(‖β‖2)=0,β1>0};

3) 存在同宿分支曲线

P={(β1,β2):5C1(0,KNL)β2+5C1(0,KNL)β1+8D1(0,KNL)β1+O(‖β‖2)=0,β1>0};

4) 存在环的折分支曲线

K={(β1,β2):C1(0,KNL)β2+C1(0,KNL)β1+2k0D1(0,KNL)β1+O(‖β‖2)=0,β1>0},

k0=0．752···.

基于系统(25)的流的两种分岔情形给出如下命题.

命题4[20]通过设计非线性控制增益，可以实现原映射(16)的1∶2 共振点附近的两种分岔情形如下.

情形3若则

1) 存在类似于pitchfork 分岔曲线F(1)的flip 分岔曲线，穿过这条曲线，映射(16) 发生倍化分岔，从平凡不动点产生周期2 不动点；

2) 存在类似于非退化Hopf 分岔曲线H(1)的非退化Neimark-Sacker 分岔曲线，穿过这条曲线，映射(16)发生Neimark-Sacker 分岔，从平凡不动点产生一个稳定的不变圈；

3) 在异宿分支曲线G附 近的指数狭窄参数区域中存在一个异宿结构，这种结构导致不变圈消失.

情形4若则

1) 仍存在类似于pitchfork 分岔曲线F(1)的flip 分岔曲线，穿过这条曲线，映射(16) 从平凡不动点产生周期2 不动点；

2) 除了存在对应情形3 中H(1)分岔曲线的非退化Neimark-Sacker 分岔曲线外，还存在类似于非退化Hopf 分岔曲线H(2)的非退化Neimark-Sacker 分岔曲线，穿过H(2)这条曲线，映射(16)发生Neimark-Sacker分岔，从两个非平凡不动点产生两个不稳定的不变圈；

3) 在同宿分岔曲线P附近的指数狭窄参数区域中存在一个同宿结构；

4) 存在对应环的折分支曲线K的分岔曲线，穿过这条曲线，映射(16)没有不变圈.

4 数值例子

本节将通过一个实例说明上述理论的可行性.将一个控制器施加到三维的二次Arneodo-Coullet-Tresser映射(简称ACT 映射)[25], 得到一个如下的四维控制系统：

图1 控制参数分岔图Fig.1 The control parameter bifurcation diagram

综上所述，命题2 中的不等式不仅可以排除参数平面上的一些不重要的参数区域，从中选出可行的参数域，还可以在不需要计算特征值模的导数的情况下，对横截条件的计算进行简化.

接着基于中心流形-范式方法来分析分岔解的类型和稳定性，通过设计非线性控制增益来实现具有期望特性的分岔解.本文将根据的符号分情况讨论1∶2 共振分岔点Q1附近局部的动力学行为.首先，基于第3 节的内容，通过计算给出确定分岔曲线的一些主要的表达式：

在k11=1．810 488 256 235 632和k12=−2．504 770 370 376 880处 ，固定非线性控制增益k22=1．6 和k31=1．4，以k21和k32为可调节的控制增益，通过计算得到如下的表达式：

情形5依据图2, 取k21=1和k32=18 ， 可知,KNL)>0.利用表达式(33)～(42)得到对应情形1 的分岔曲线如下：

图2 0,KNL)的曲线图Fig.2 The graph of ,KNL)

pitchfork 分岔曲线F(1)=55．518 022 97+44．129 26k11+54．062 25k12;

非退化的Hopf 分岔曲线H(1)=108．704 079 7+84．066 000 70k11+104．163 072 8k12;

异宿分支曲线G=8．192 489 252+6．470 410 056k11+7．947 670 516k12.

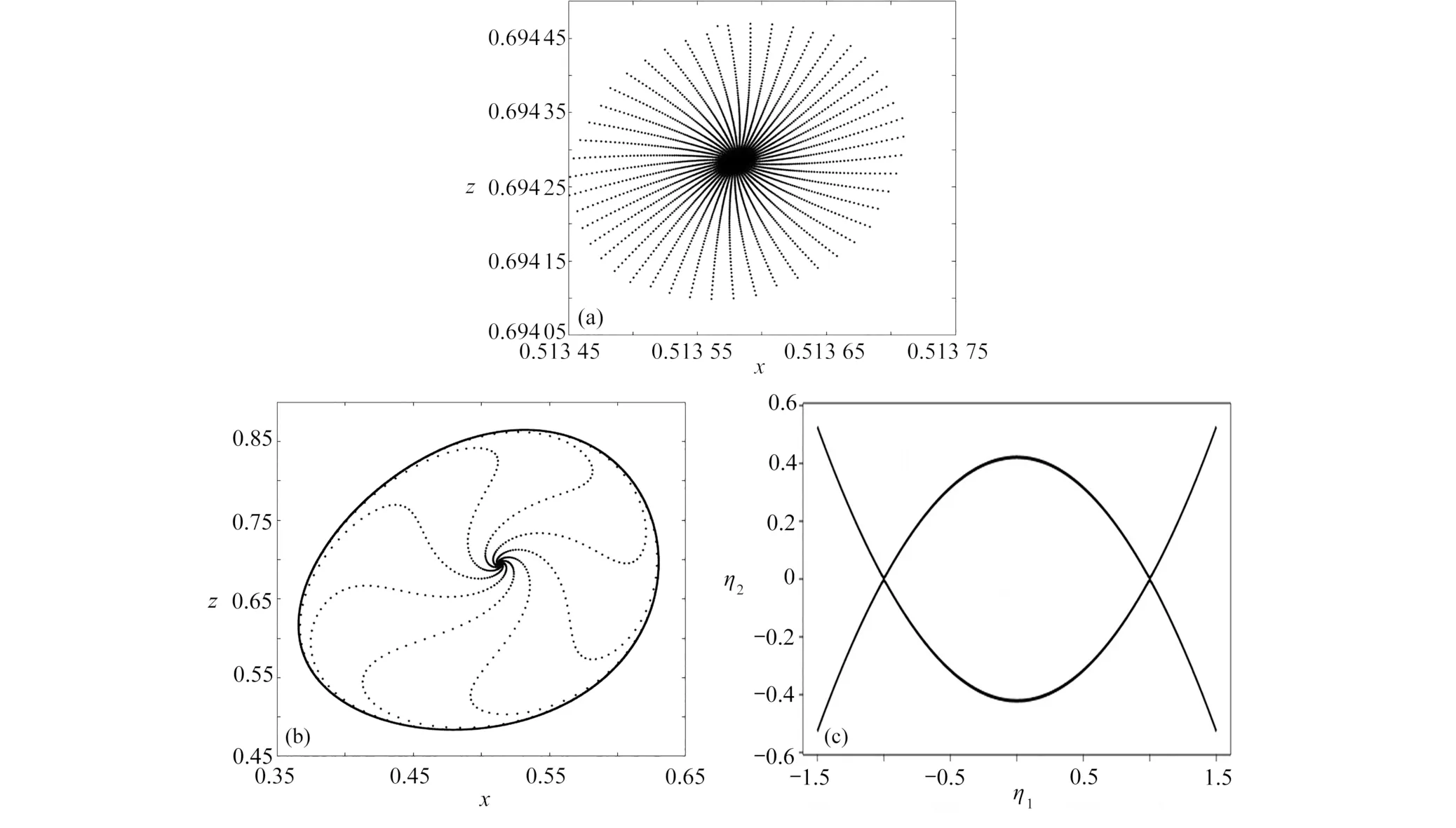
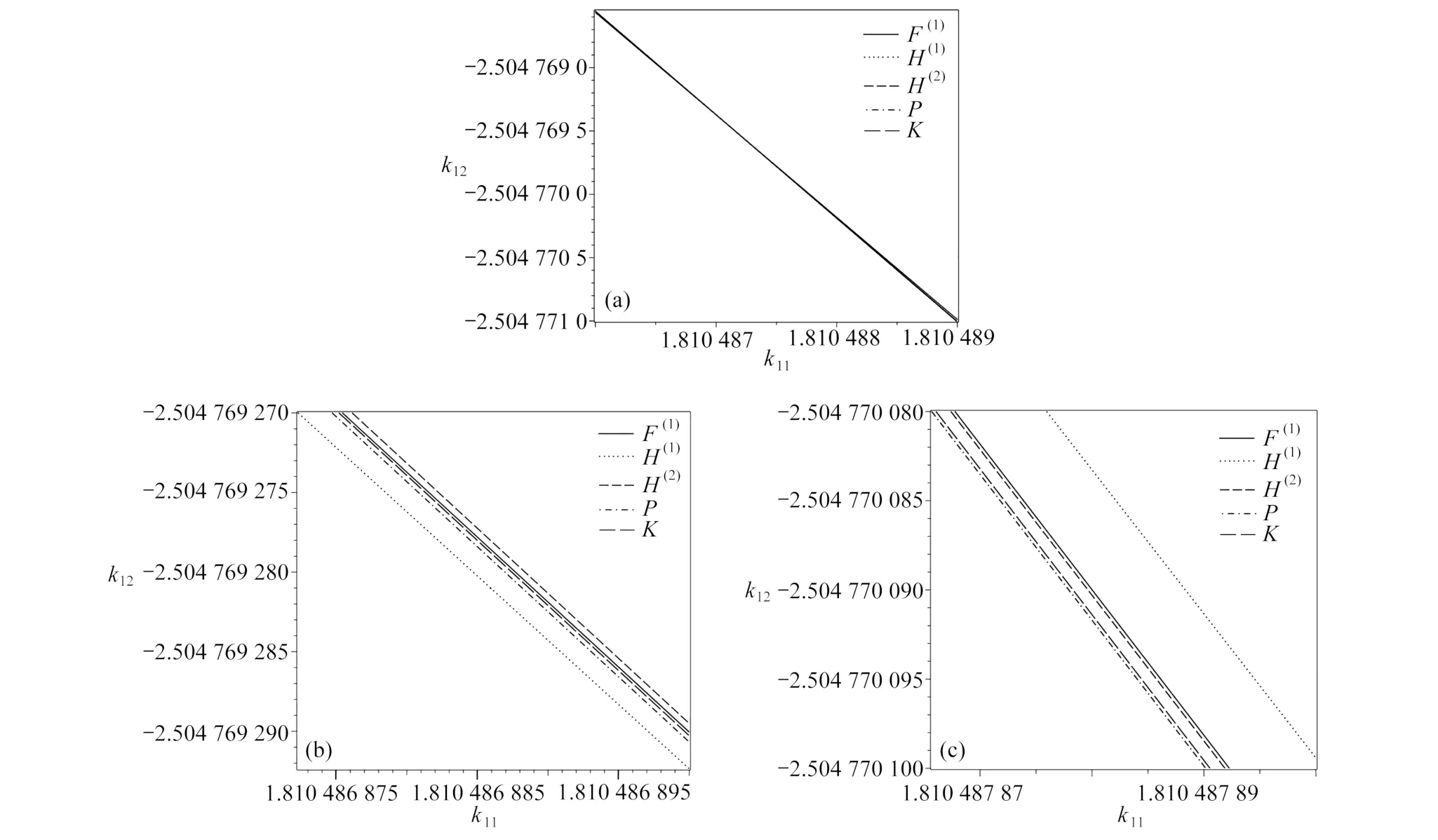
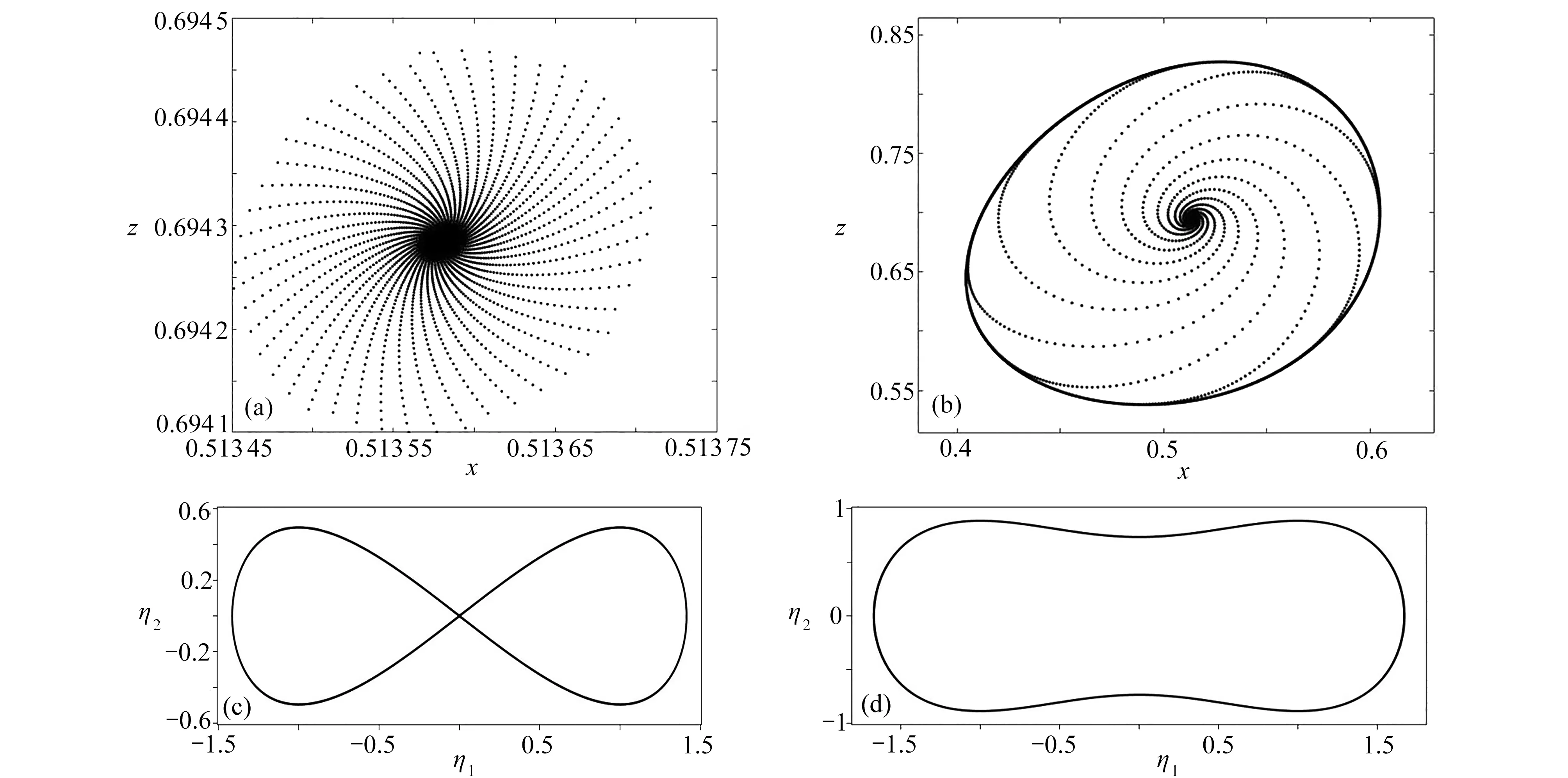
在1．810 44

图3 控制系统(29)对应情形5 形如式(20)的范式映射的分岔图：(a) 时，系统(29)对应的分支图；(b) 对应于图3(a)分岔点上半部分的局部放大图；(c) 对应于图3(a)分岔点下半部分的局部放大图Fig.3 Bifurcation diagrams of the normal form mapping like eq.(20) of control system (29) corresponding to case 5: (a) the bifurcation diagram for system(29), (b) the local enlargement of the upper half of the bifurcation points in fig.3(a); (c) the local enlargement of the lower half of the bifurcation points in fig.3(a)

在分岔参数点Q1的 小邻域内取控制参数 (k11,k12)=Q1+(−0．08,0．15)，通过控制获得了一个唯一的稳定不动点，其相图如图4(a)所示；当穿过分岔曲线F(1)，从该不动点处会产生两个不稳定的不动点；当穿过非退化的Hopf 分岔曲线H(1)时，在 (k11,k12)=Q1+(−0．1,−0．01) 处映射(29)发生Neimark-Sacker 分岔，产生一个如图4(b) 中所示的稳定的不变圈；当穿过异宿分支曲线G时(见图4(c)) ，不变圈消失.

图4 对应于图3 所示分岔图的相图：(a) 在( k11,k12)=Q1+(−0．08,0．15) 处的稳定点；(b) 在 ( k11,k12)=Q1+(−0．1,−0．01)处的不变圈；(c) 异宿分支曲线G 上的异宿轨道Fig.4 Phase diagrams corresponding to the bifurcation diagrams shown in fig.3: (a) the fixed point at (k 11,k12)=Q1+(−0．08,0．15); (b) the invariable circle at ( k ,k )=Q+(−0．1,−0．01); (c) the heterotropic orbit on heterotropic curve G

情形6依据图2, 取k21=1．3和k32=1．8， 可知<0.利用表达式(33)～(42)得到对应情形2 的分岔曲线如下.

Pitchfork 分岔曲线F(1)=55．518 022 97+44．129 26k11+54．062 25k12;

非退化的Hopf 分岔曲线H(1)=108．704 079 7+84．066 000 70k11+104．163 072 8k12;

非退化的Hopf 分岔曲线H(2)=9．869 602 502+7．865 381 192k11+9．625 545 552k12;

同宿分支曲线P=38．530 639 71+30．728 569 23k11+37．594 004 08k12;

环的折分支曲线K=7．186 894 048+5．732 993 682k11+7．013 182 081k12.

在1．810 486

图5 控制系统(29)对应情形6 形如式(20)的范式映射的分岔图：(a) <0 时，系统(29)对应的分支图；(b) 对应于图5(a)分岔点上半部分的局部放大图；(c) 对应于图5(a)分岔点下半部分的局部放大图Fig.5 Bifurcation diagrams of the normal form mapping like eq.(20) of control system (29) corresponding to case 6: (a) the bifurcation diagram of system(29), 0; (b) the local enlargement of the upper half of the bifurcation points in fig.5(a); (c) the local enlargement of the lower half of the bifurcation points in fig.5(a)

在分岔参数点Q1的 小邻域内取控制参数(k11,k12)=Q1+(−0．11,0．12)，存在一个唯一的不动点，其相图如图6(a)所示；当穿过非退化的Hopf 分岔曲线H(1)时 ，在 (k11,k12)=Q1+(−0．1,−0．05) 处映射(29)发生Neimark-Sacker 分岔，产生一个如图6(b)中所示的稳定的不变圈；当穿过非退化的Hopf 分岔曲线H(2)时，映射(29) 发生Neimark-Sacker 分岔，产生两个不稳定的不变圈；当穿过同宿分支曲线P时(见图6(c))，上述的其中一个不稳定的不变圈消失，并且额外出现一个稳定的不变圈；当穿过环的折分支曲线K时(见图6(d))，所有不变圈消失.

图6 对应于图5 所示分岔图的相图：(a) 在 ( k11,k12)=Q1+(−0．11,0．12) 处的稳定点；(b) 在 ( k11,k12)=Q1+(−0．1,−0．05) 处的不变圈；(c) 同宿分支曲线P 上的同宿轨道；(d) 环的折分支曲线K 上的轨道Fig.6 Phase diagrams corresponding to the bifurcation diagrams shown in fig.5: (a) the fixed point at (k 11,k12)=Q1+(−0．11,0．12); (b) the invariable circle at ( k11,k12)=Q1+(−0．1,−0．05); (c) the homoclinic orbit on homoclinic curve P; (d) the orbit on the folded branch curve of ring K

5 结 论

本文提出一套完整的非线性控制策略，研究了离散动力系统1∶2 共振情形下的余维二分岔的反控制问题.针对四维离散控制系统(或映射), 建立了1∶2 共振分岔的显式准则，克服了传统分岔准则在反控制过程中需要依赖直接计算特征值带来的困难，这将更适合含有多个控制增益的离散动力系统此类余维二分岔控制的设计.本文随后推导获得了1∶2 共振的中心流形，将含参数的四维映射简化为二维的范式映射，得到了控制分岔解类型和稳定性关键指标的解析表达式.基于理论分析，本文针对一个ACT 映射通过该控制策略在指定的参数位置处成功实现了1∶2 共振情形下的Neimark-Sacker 分岔以及更加复杂的同异宿分岔.