基于CEEMDAN⁃SPSO⁃ELM的旋转电机滚动轴承故障检测方法

宋绍楼，吕亮，刘昕明

基于CEEMDAN⁃SPSO⁃ELM的旋转电机滚动轴承故障检测方法

宋绍楼，吕亮，刘昕明

（辽宁工程技术大学 电气与控制工程学院，辽宁 葫芦岛 125105）

由于旋转电机滚动轴承振动信号存在不平稳、非线性的特征，传统时频分析法、小波分解法存在在信号分解过程中能量泄露、自适应能力差的问题，经验模态分解（EMD）法存在模态混叠等问题。提出一种基于噪声自适应完备总体平均经验模态分解方法（CEEMDAN），利用具有麻雀捕食预警机制的粒子群算法（SPSO）优化极限学习机神经网络（ELM）的CEEMDAN⁃SPSO⁃ELM算法。利用所提方法对滚动轴承单一与多种损伤故障进行分析诊断，结果表明，所提算法具有有效性及诊断准确性。

旋转电机滚动轴承； 故障诊断； CEMMDAN； ELM； SPSO

组成电机的各种部件中，滚动轴承由于受高温、强冲击、制造工艺以及装配不良等因素的影响极易发生故障，进而影响电机的正常运行。为保障电机能够正常运行，对滚动轴承故障诊断技术进行研究是非常必要的[1⁃2]。

随着对智能算法研究的不断深入，BP、ELM、深度学习等神经网络方法[3⁃4]，支持向量机方法[5]，专家诊断系统[6]等方法越来越多地应用到滚动轴承故障诊断技术中。文献[7]采用小波分析法对采集的原始信号进行特征提取，利用支持向量机的方法对故障状态进行识别。但是，文献[7]中人工参数设置的方法存在识别自适应能力差以及识别精度低的问题。针对这个问题，文献[8]利用智能算法对支持向量机参数进行优化，既提高了算法的识别效果，同时也提高了算法的自适应能力。文献[9]采用加权排列熵以及优化的ELM，对滚动轴承进行故障诊断。文献[10]采用改进的遗传算法优化ELM对旋转电机滚动轴承进行故障诊断。ELM的训练、运算速度以及泛化能力相对于其他方法具有较大的优势，但是存在预测诊断精度不高的问题。为提高滚动轴承故障诊断的精度与速度，本文提出一种基于CEEMDAN⁃SPSO⁃ELM的滚动轴承故障诊断方法。首先，利用CEEMDAN模态分解方法对所采集的信号进行分解以得到各IMF分量；其次，利用能量矩方法对IMF分量进行处理，进而得到原始信号特征向量；然后，利用经SPSO算法优化的ELM神经网络对滚动轴承故障类型进行诊断分析；最后，对所提方法的有效性及诊断精度进行分析验证。

1 信号采集与特征提取

1.1 振动信号采集平台

振动数据采集于美国西储凯斯大学轴承检测中心数据库。信号采集平台主要由扭转传感器、测力计以及额定功率为1.5 kW的三相感应电机组成。实验时，利用电火花技术分别在滚动轴承内圈、外圈及滚动体的两处位置上制造0.177 8、0.355 6、0.533 4 mm及0.711 2 mm的损伤。

1.2 基于CEEMDAN与能量矩的特征提取方法

为了对滚动轴承振动信号进行特征提取，首先利用CEEMDAN模态分解方法对原始振动信号进行模态分解[12]。CEEMDAN是一种具有自适应高斯白噪声掺入的模态分解方法，该方法对信号分解所得的各个IMF分量正交性能好，恢复误差小，因而对原始信号的表征能力强。CEEMDAN模态分解方法的设置参数为：噪声比为0.02，迭代次数为20，噪声加入次数为200次，原始振动信号采样点12 000 个。CEEMDAN分解原始滚动轴承振动信号前四个分量的分解效果如图1所示。

图1　CEEMDAN分解原始滚动轴承振动信号前四个分量的分解效果

对分解的各IMF分量利用能量矩与归一化方法进行信号特征向量的提取。能量矩是一种结合时间尺度的信号能量计算方法，由于考虑了时间尺度，因而对原始信号的表征能力强。IMF分量（E）及余项分量（E）计算表达式为：

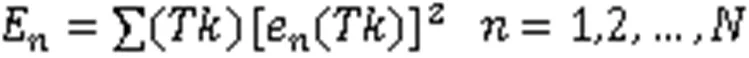
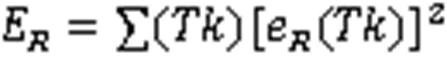
式中，为采样周期；为采样点数。

最后，对各IMF分量进行归一化处理，以获取信号特征向量。

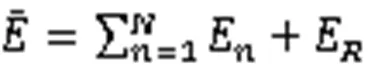
利用CEEMDAN模态分解方法对原始旋转电机滚动信号进行分解，然后利用能量矩特征提取方法求解旋转电机滚动轴承在四种运行状态下的特征向量。滚动轴承特征向量如图2所示。

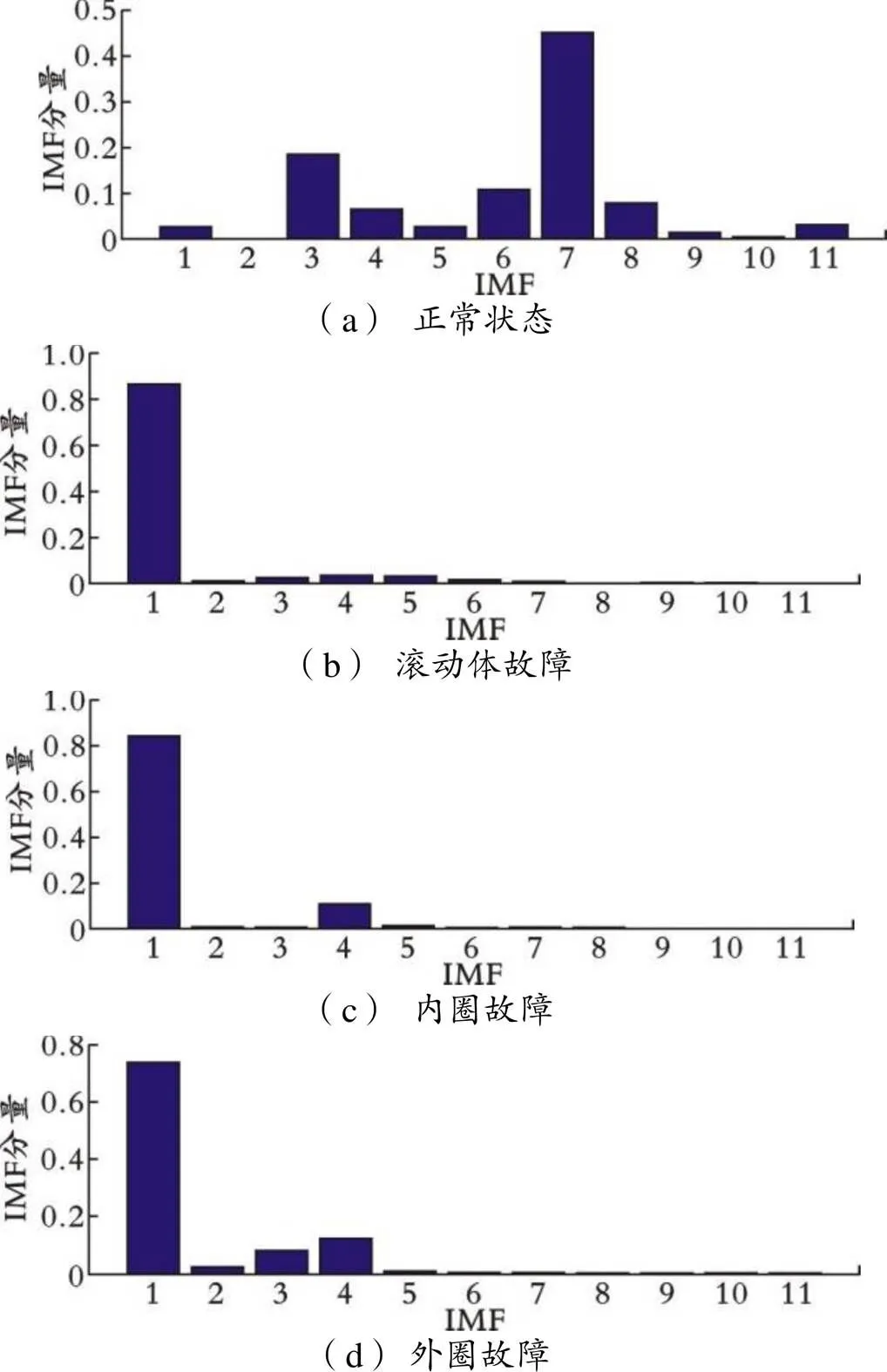
图2　滚动轴承特征向量

由图2可看出，前几个IMF分量所占据的能量最多，能有效地对原始信号进行表征。因此，后续研究均取前7个IMF分量作为特征IMF分量。

2 SPSO⁃ELM故障诊断方法

2.1 SPSO算法

使用麻雀搜索算法（SSA）随机预警机制对原始粒子群优化算法（Partical Swarm Optimization， PSO）迭代结果进行随机扰动，即以SPSO（SSA Partical Swarm Optimization）算法抑制其陷入局部解[12⁃14]。利用SPSO算法对维、个个体的粒子种群进行初始化，其个体位置可由X=(x1，…，x)表示，则种群可由=(1，…，X)表示，粒子的迭代过程为：

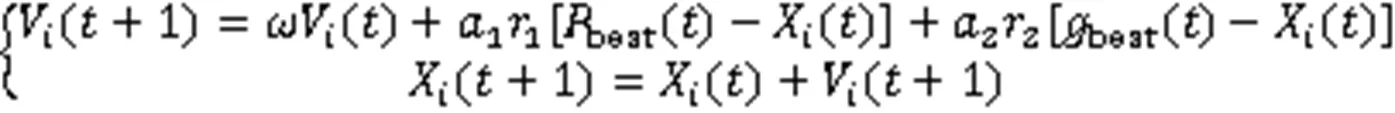
式中，V（）为当前代粒子移动速度；为惯性权重因子；1为自我学习因子；2为社会学习因子；1与2均为服从（0,1）均匀分布的随机数；best（）为个体最优解；best（）为全局最优解。采用式（6）的随机权重更新方法，以提高算法的收敛速度。

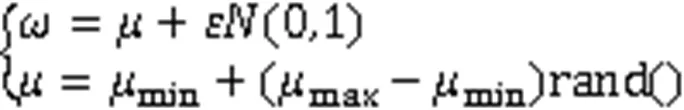
引入麻雀搜索算法的随机预警机制，即从种群中随机选择一定比例的粒子作为预警粒子，所选择的粒子更新方式为：

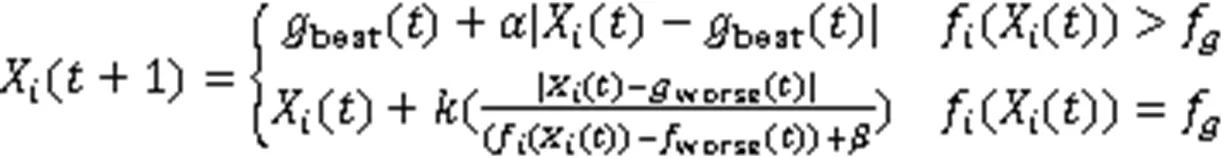
当预警粒子处于距最优位置较远的位置时，将向最优位置移动；当预警粒子位置处于最优位置时，则会向其他位置移动。由此可知，随机预警机制的引入能够极大地降低算法陷入局部解的可能，SPSO算法运行流程如图3所示。

2.2 SPSO⁃ELM算法建模

ELM神经网络因其具有训练速度快、泛化能力强以及误差小等优势而被广泛应用于工程实践。ELM神经网络其隐含层权值以及偏移值是以随机分配的形式产生的，也就是这个随机参数分配很有可能使ELM神经网络所得参数并不是最优的，进而影响ELM神经网络预测与分类的准确度。针对这个问题，使用SPSO算法对ELM神经网络进行优化，从而建立SPSO⁃ELM神经网络模型。

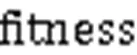
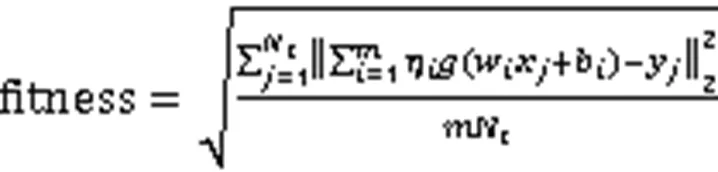
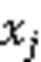
SPSO⁃ELM算法的计算过程为：首先，对ELM神经网络的结构进行确定，以便于确定SPSO算法每个个体的维度。若样本的维数为，隐含层神经元节点数量为，那么SPSO算法个体维度应为（+1）×。然后，初始化SPSO算法参数，包括种群数量、迭代次数、随机预警粒子比例以及学习因子等。将训练集样本输入ELM神经网络中，并利用SPSO算法对ELM神经网络隐含层权值以及偏移值进行优化，使式（8）的适应度函数达到最小。

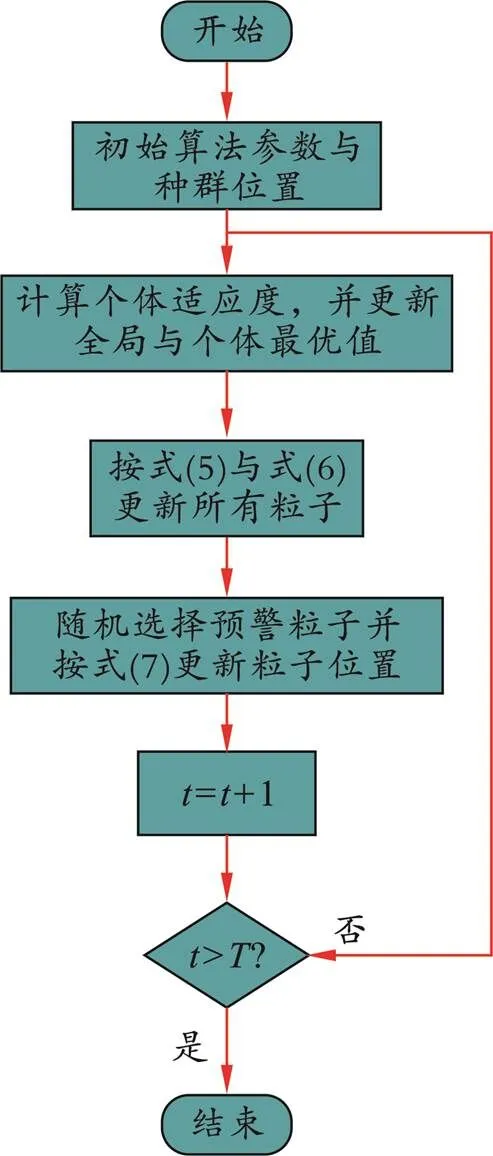
图3　SPSO算法运行流程

综上SPSO⁃ELM神经网络算法的具体流程为：

步骤1 对预处理得到的数据进行读取。

步骤2 设置SPSO算法参数，并初始化SPSO算法粒子位置。

步骤3 训练ELM神经网络，并计算当前粒子适应度。

步骤4 更新粒子位置与速度。

步骤5 将隐含层权值与偏移值导入ELM神经网络。

步骤6 测试网络并计算误差，更新粒子适应度，并获取最优位置。

步骤7 若没有达到迭代终止条件，返回步骤4；到达终止条件停止迭代。

3 仿真验证

利用CEEMDAN⁃SPSO⁃ELM方法对旋转电机滚动轴承故障诊断验证的具体流程为：首先利用CEEMDAN模态分解方法对原始诊断信号进行分解；随后将得到的各个IMF分量利用能量矩与归一化处理方法进行特征向量计算，并将所得的特征向量分为训练数据集与测试数据集；最后利用训练数据集对SPSO⁃ELM神经网络进行训练，利用测试数据集对SPSO⁃ELM神经网络进行测试，并与ELM、PSO⁃ELM神经网络进行对比验证该方法的适用性。

3.1 损伤诊断数据

选取采样频率为12 kHz时正常运行，滚动体故障、内圈故障以及外圈故障4种状态数据。每种工作状态分别截取80组数据，每组数据的数据量为1 200个，每种工作状态下采样数据总数为96 000个。针对每种工作状态下的80组数据利用CEEMDAN模态分解方法以及能量矩方法分别做特征向量提取，对所提取的特征向量均取前7个数据1、2、3、4、5、6、7作为本组数据的特征向量。

本文选取旋转电机运行于1 772 r/min、损伤程度为0.533 4 mm、采样频率为12 kHz时的数据作为单一损伤数据，4种工作状态分别截取80组数据，共获取320组数据，其中的240组数据作为训练集样本数据，80组作为测试集样本数据。旋转电机滚动轴承单一损伤4种工作状态下训练集与测试集部分样本数据分别如表1-2所示。

对多种损伤数据，由于电机在1 750 r/min运行时与在1 772 r/min正常运行时，数据特征几乎一样，振动信号频率均为固有频率，因而在处理过程中，分别选取正常状态、0.533 4 mm损伤程度下3种故障状态以及0.177 8 mm损伤程度下3种故障状态各80组数据，数据组总数为560组，其中420组数据作为训练集样本数据，140组作为测试集样本数据，具体数据出于篇幅考虑不再给出。

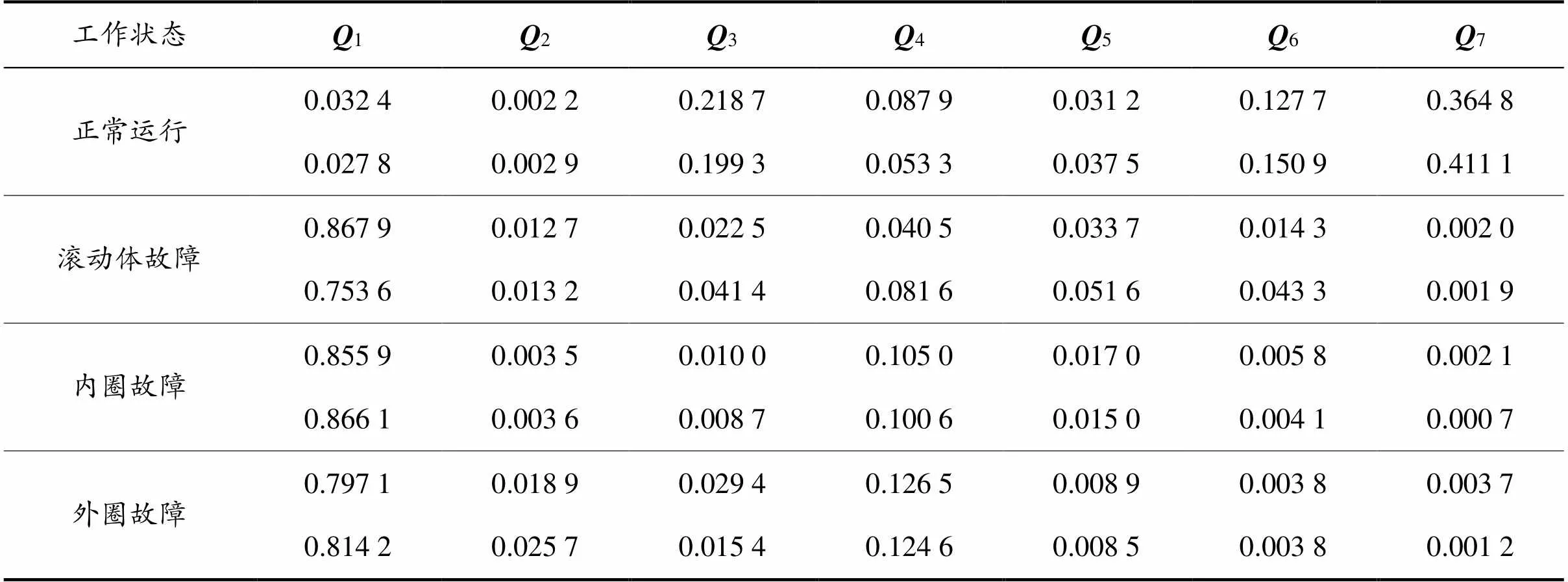
表1　旋转电机滚动轴承单一损伤4种工作状态下训练集部分样本数据

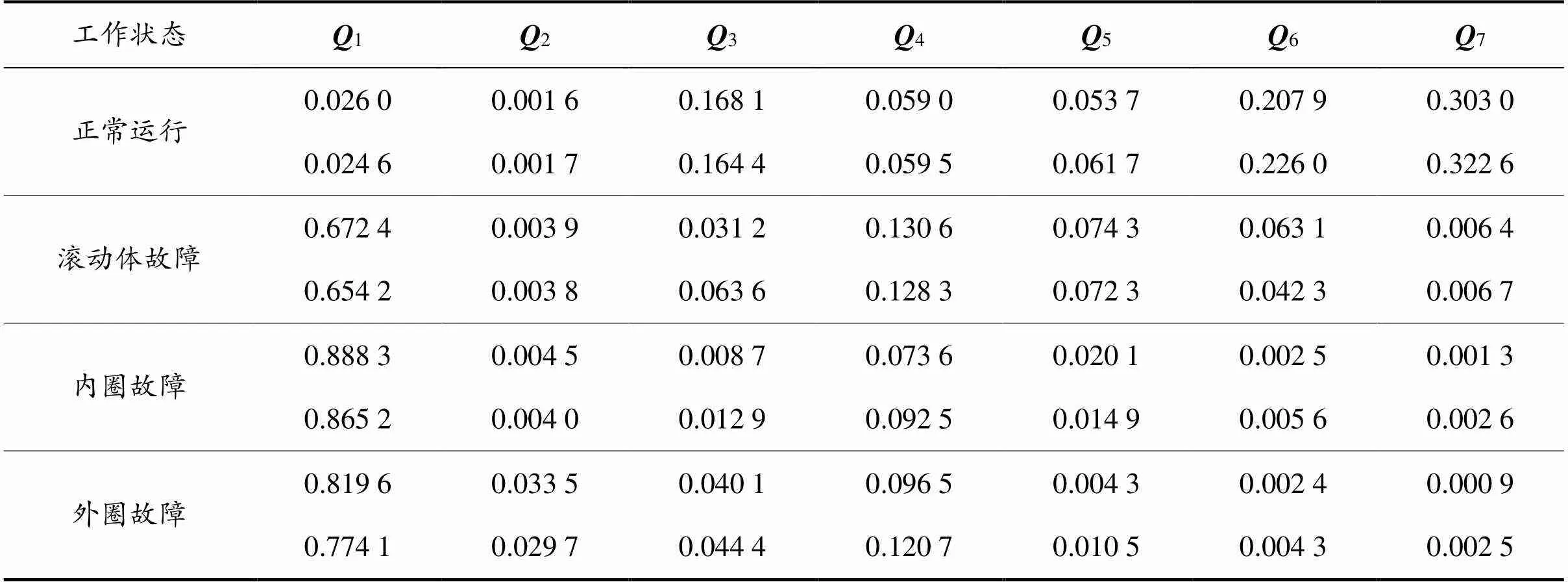
表2　旋转电机滚动轴承单一损伤4种工作状态下测试集部分样本数据

3.2 损伤诊断实验

采用ELM、PSO⁃ELM以及SPSO⁃ELM三种算法对单一损伤进行预测。PSO、SPSO算法的粒子种群数量均为20，迭代次数均为100次；PSO算法的1与2均为1.5，为0.5；SPSO算法的1与2均为1.5，min与max分别为0.6与0.8，为0.3，随机预警与发现粒子百分比均为20%；ELM神经网络映射核函数为ReLU核函数，隐含层神经元节点数目为20个。测试集单一损伤诊断结果如图4所示。图中，纵坐标1-4分别表示正常状态、滚动体受损深度0.533 4 mm的状态、内圈受损深度0.533 4 mm的状态以及外圈受损深度0.533 4 mm的状态。

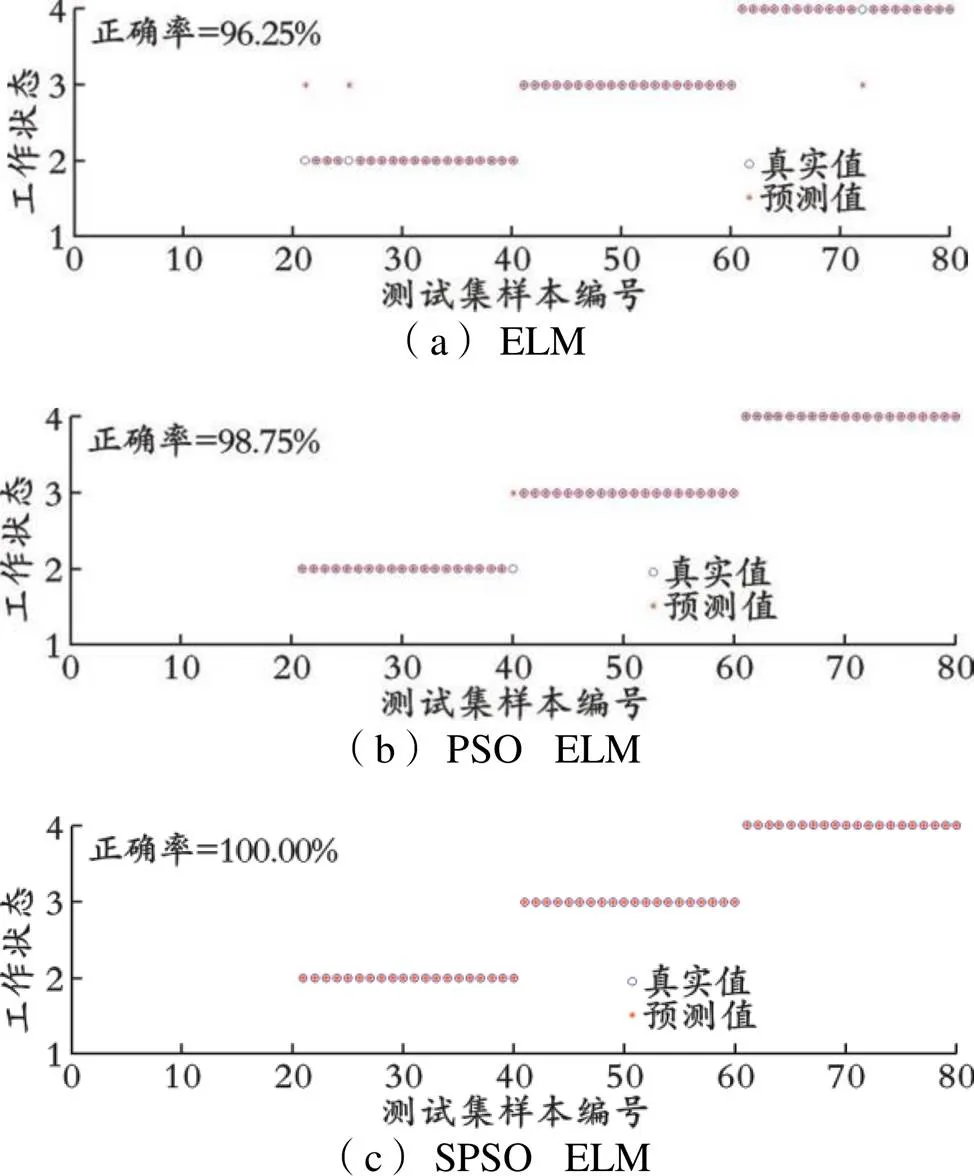
图4　测试集单一损伤诊断结果

由图4可以看出，所提出算法无论在求解准确度还是在泛化能力上都优于传统的ELM算法与PSO⁃ELM算法，SPSO⁃ELM算法相对于单纯ELM算法准确度提高3.75%，比PSO⁃ELM算法准确度提高1.25%。

在不改变上述算法参数的前提下，对旋转电机滚动轴承多种损伤程度进行诊断，测试集多种损伤诊断结果如图5所示。图中，纵坐标1-7分别表示正常状态、滚动体受损深度0.533 4 mm的状态、内圈受损深度0.533 4 mm的状态、外圈受损深度0.533 4 mm的状态、滚动体受损深度0.177 8 mm的状态、内圈受损深度0.177 8 mm的状态及外圈受损深度0.177 8 mm的状态。

图5　测试集多种损伤诊断结果

由图5可以看出，诊断结果再次验证了SPSO⁃ELM神经网络算法在旋转电机滚动轴承故障诊断中的优势，其测试集的正确率相对其他两种算法分别高了4.29%与2.14%，说明所提算法在对ELM神经网络优化计算中具有非常高的预测准确度，再次验证了所提算法在泛化能力方面的优势，由此可知所提算法具有非常好的应用前景与价值。

4 结 论

为了提高旋转电机滚动轴承故障诊断精度，提出基于CEEMDAN⁃SPSO⁃ELM的旋转电机滚动轴承故障检测方法。利用CEEMDAN模态分解方法结合能量矩对所获取的旋转电机滚动轴承振动信号进行提取，并利用SPSO⁃ELM神经网络方法分别对旋转电机单一损伤故障以及多种损伤故障进行了诊断实验，通过对比实验验证了所提算法的有效性及诊断的精准性。

［1］ Wang H， Chen J， Zhou Y， et al. Early fault diagnosis of rolling bearing based on noise⁃assisted signal feature enhancement and stochastic resonance for intelligent manufacturing［J］. The International Journal of Advanced Manufacturing Technology， 2020，107：1017⁃1023．

［2］ Li C， Zheng J， Pan H， et al. Refined composite multivariate multiscale dispersion entropy and its application to fault diagnosis of rolling bearing［J］. IEEE Access，2019，7：47663⁃47673．

［3］ Zhang L P，Liu H M，Lu C. Fault diagnosis technology of rolling bearing based on LMD and BP neural network［C］// 2016 12th World Congress on Intelligent Control and Automation （WCICA）. Guilin ：IEEE，2016.

［4］ Gunerkar R S， Jalan A K， Belgamwar S U. Fault diagnosis of rolling element bearing based on artificial neural network［J］. Journal of Mechanical Science and Technology， 2019， 33（2）：505⁃511.

［5］ Li Y， Zhang W， Xiong Q， et al. A rolling bearing fault diagnosis strategy based on improved multiscale permutation entropy and least squares SVM［J］. Journal of Mechanical Science and Technology， 2017， 31（6）：2711⁃2722.

［6］ Ma J， Wu J D， Fan Y G， et al. Fault diagnosis of rolling bearing based on the PSO⁃SVM of the mixed⁃feature［J］. Applied Mechanics & Materials， 2013， 380⁃384：895⁃901.

［7］ 谢国民，王灿祥，佟莹.采煤机电动机故障诊断专家系统的研究与应用［J］.信息与控制，2013，42（3）：358⁃363.

［8］ 吕维宗，王海瑞，舒捷.基于谐波小波包和IAGA⁃SVM的滚动轴承故障诊断［J］.计算机应用与软件，2019，36（10）：30⁃38.

［9］ 张旭.基于加权排列熵和ELM的通风机轴承故障诊断研究［D］.徐州：中国矿业大学，2020.

［10］ 皮骏，马圣，杜旭博，等.基于BQGA⁃ELM网络在滚动轴承故障诊断中的应用研究［J］.振动与冲击，2019，38（18）：192⁃200.

［11］ 卓仁雄.基于CEEMDAN和GWO⁃SVM的电机滚动轴承故障诊断［D］. 衡阳：南华大学，2018.

［12］ 尤田，张威，葛琳琳.基于GA⁃PSO算法焊接机器人路径规划研究［J］.辽宁石油化工大学学报，2018，38（2）：85⁃89.

［13］ 唐玲玲，缪希仁，庄胜斌.PSO⁃ELM在低压系统短路电流峰值预测中的应用［J］.福州大学学报（自然科学版），2020，48（4）：471⁃478.

［14］ 杨博雯，钱伟懿.粒子群优化算法中惯性权重改进策略综述［J］.渤海大学学报（自然科学版），2019，40（3）：274⁃288.

Fault Detection Method for Rolling Bearings of Rotating Electrical Machines Based on CEEMDAN⁃SPSO⁃ELM

Song Shaolou， Lü Liang， Liu Xinming

（Faculty of Electrical and Control Engineering， Liaoning Technical University， Huludao Liaoning 125105， China）

In view of the unstable and nonlinear characteristics of the rolling bearing vibration signal of rotating electrical machines, the traditional time⁃frequency analysis method and wavelet packet decomposition method have energy leakage and poor adaptive ability in the signal decomposition process, and the EMD decomposition method has modal aliasing and other problems. In order to improve the fault diagnosis accuracy of rolling bearings, CEEMDAN combined with energy moment method is proposed to extract the original vibration signal features. The weight and offset of ELM hidden layer are optimized by SPSO algorithm, and the CEEMDAN⁃SPSO⁃ELM method is used to analyze and diagnose single and multiple damage faults of rolling bearings.The effectiveness of the algorithm and the improvement of diagnosis accuracy are verified by comparative experiments.

Rotating electric machine rolling bearing； Fault diagnosis； CEMMDAN； ELM； SPSO

TH17

A

10.3969/j.issn.1672⁃6952.2022.01.015

1672⁃6952（2022）01⁃0086⁃06

2020⁃11⁃04

2020⁃11⁃23

辽宁省教育厅科学研究基金项目（LJY013）。

宋绍楼（1964⁃），男，硕士，教授级高级工程师，从事工业过程控制与优化研究；E⁃mail：lngdssl@qq.com。

吕亮（1994⁃），男，硕士研究生，从事智能检测与信息处理研究；E⁃mail：lv_liang1230@163.com。

http：//journal.lnpu.edu.cn

（编辑 陈 雷）