4SW- 170 型马铃薯挖掘机的振动模型与频率分析

内蒙古开放大学 付昱

对于摆动式马铃薯挖掘机而言，因其主要工作机理是利用摆动筛的往复摆动进行马铃薯和土壤的分离工作，正常工作时的振动不可避免，而由于设计工作频率和机器本身固有频率过于接近容易造成共振，从而使得机器产生一种不规则的高频率和高幅值的振荡，那么这种状态下工作就容易造成装配在机架各个部位的工作部件疲劳断裂，影响机械设备的使用可靠性。如果能够通过理论计算结合试验的方式找到引起机械结构不规则振动的原因，在试验样机阶段调整机械的动力学参数，使额定转速下各部件运转频率避开结构的固有频率，以免工作在临界转速条件下，进而有效提高产品质量[2]。

1 力学模型的建立

4SW-170 马铃薯挖掘机如图1 所示，工作中拖拉机的悬挂机构与悬挂机架上的三点悬挂处相连，传动机构1 通过万向节传动轴与拖拉机的动力输出轴连接。拖拉机的动力由安装在传动机构1 两端的偏心链轮2 分别通过链条传给升运链轴3，使其转动，通过连杆传给摆动筛前梁5，使其摆动[1]。

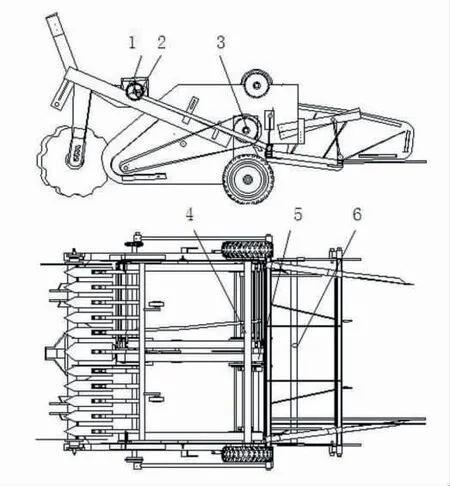
图1 4SW- 170 型马铃薯挖掘机两视图

组成机械系统的构件形状各异，构件间的连接方式也互不相同，因而进行运动学分析首先需要把机械系统和机械构件简化成可供研究的力学模型。力学模型的建立方法一般采用变无限为有限，既将连续系统离散为离散系统，同时也可以使机械系统中有较大的惯性和刚度，而弹性较小的构件视为质量块，惯性较小、柔度较大的构件视为无质量的弹簧[3]。在本文中做如下假设以简化振动系统的力学模型：

（1）将机架与摆动筛筛台的连接视为刚性连接；

（2）本文同时考虑路面的随机激励、挖掘铲冲击和两个传动系统产生的惯性力引起的振动。

根据前期试验结果证明，机架主要振动激励来源于三个方面：P（t）为自身质量在万有引力和路面不平度的作用下引起的激励力，F0（t）为挖掘铲的激振力，F1（t）为主轴转子惯性力，F2（t）为升运轴转子产生的惯性力，F3（t）为摆动筛的激振力。将马铃薯挖掘机简化成具有垂向振动Z、横向振动Q、纵向振动Ф 的三振动系统，机架系统的质量为m，质心为直角坐标系原点o。建立整机振动系统模型如图2 所示：

图2 挖掘机机体振动模型

其中u1-u4分别为两个车轮和两个圆盘处路面的随机位移激励，即路面不平度；

k1~k4为两个车轮以及两个圆盘和机架间的等效刚度；

c1~c2为2 个车轮和土壤间作用时耦合的等效阻尼；

a 为左右两侧车轮到X 轴的距离；

l1~l2分别为两个车轮轴和两个圆盘切刀到Y 轴的距离；

x1~y1分别为主轴传动系统垂直惯性力的作用点到Y 轴和X 轴的距离；

x2~y2分别为升运链传动垂直惯性力作用点到Y轴和X 轴的距离；

x3~y3分别为摆动筛传动垂直惯性力作用点到Y轴和X 轴的距离。

2 建立质心振动微分方程

根据动力学定律，建立振动方程：

垂向位移的自由度运动方程：

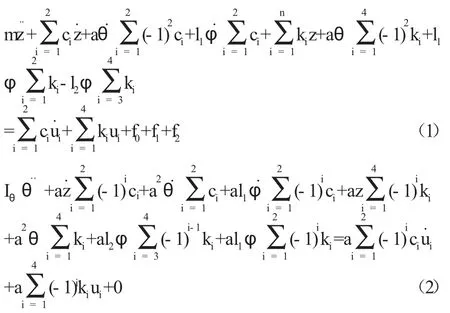
纵向位移的运动方程：

写成矩阵形式：

其中：

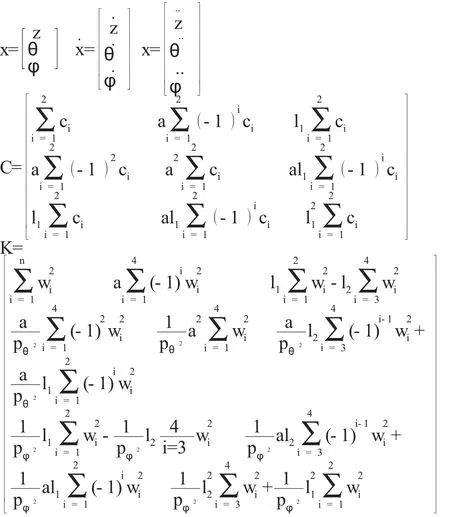
其中方程4 为挖掘机在四种激励作用下的矩阵形式的耦合振动方程，其中M 为质量矩阵，C 为阻尼矩阵，K 为刚度矩阵。令挖掘机振动系统的位移坐标向量

将矩阵写成如下形式：

对方程进行拉普拉斯Laplace 变换:若Es2As+B 是非奇异矩阵，则逆矩阵存在那么振动系统的传递函数：

设矩阵Q=Es2As+B，将矩阵E,A,B 代入矩阵Q 运算，将矩阵输入MATLAB，求其秩为3，则Q 是非奇异矩阵，其逆矩阵存在，则矩阵可写为：

挖掘机静止空载只驱动摆动筛摆动方程:

挖掘机静止空载驱动主轴和升运轴运转方程：

挖掘机静止空载驱动摆动筛和主轴和升运轴运转方程：

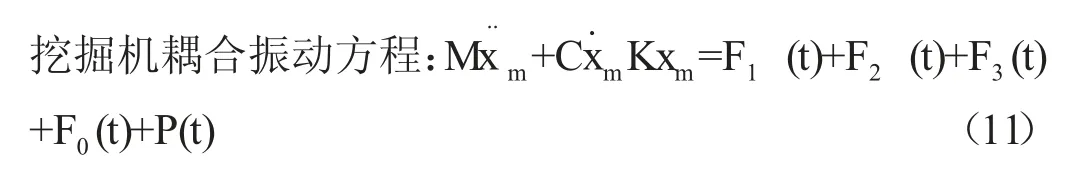
3 筛体- 机架系统振动模型

单独建立筛体- 机架的振动模型如图3 所示：

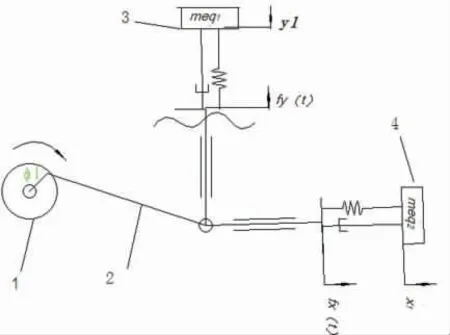
图3 摆动筛- 机架振动系统模型

系统垂向振动的微分方程为:

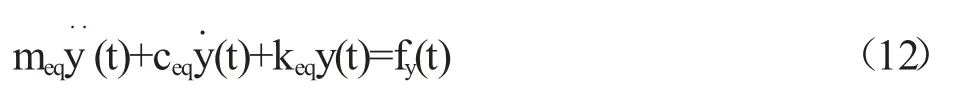
两边同除以meq将式（12）写为：

进行傅立叶变换，得：

其中，位移和力的傅立叶变换分别为：

式中：j 为单位虚数，即。令：

得到单自由度的位移频响函数：

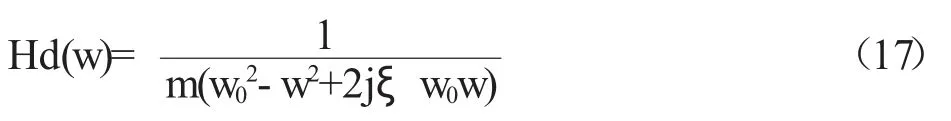
由傅氏变换的性质得到加速度频响函数：

频响函数可表达为实部和虚部的形式：

式中：meq1为垂向等效质量；ceq为垂向等效阻尼；

4 基于模型的频率分析

模态是机械结构的固有振动特性，每一个模态都对应于特定的固有频率、阻尼比和模态振型。通过模态分析方法搞清楚4SW-170 型马铃薯挖掘机的各阶主要模态特性，就可以预言马铃薯挖掘机在结构设计所需要的频段内，在外部或内部各种振源作用下产生的实际振动响应。根据所建摆动筛- 机架振动模型可知，简化后的摆动筛- 机架振动系统是线性系统，根据功率谱密度分析方法可知输入信号（摆动筛运动）和输出信号（机架振动）的两者之间存在以下的谱密度关系[1]：

其中：Sy（ω）为输出的功率谱密度，Sx（ω）为输入的功率谱密度。频率响应函数与谱密度之间的关系为：

上式即为利用谱分析法求频率响应H(ω)的基本公式，MATLAB 函数工具箱提供了tfe 函数用来实现基于经典谱估计的系统辨识，其调用方式为：Txy=tfe(x,y,NFFT,Fs,window) 该函数使用了welch 平均周期图算法，根据输入变量x 和输出变量y 来估计系统的传递函数。参数window 用来指定所采用的窗函数，窗函数的长度必须与向量x 的长度一样大。在本文中x 为输入的摆动筛振动加速度信号，y 为输出的机架质心附近振动加速度信号。将上述分析得到的频响函数实部和虚部作为输入数据，可以进行振动系统参数识别，通过MATLAB 程序进行求解，对机架前后和垂直方向的振动频响函数采用levy 算法进行拟合，对轴向振动频响函数采用ITD 方法拟合，所得结果如表所示：

表1 机架固有频率表（HZ）

5 结论

马铃薯挖掘机主机的振动与主机机架等零部件尺寸、固有频率、阻尼系数及作用在收获机结构上的载荷等有关。通过建立振动模型结合试验和频率分析方法找到主机机架的固有频率，及时调整机械的动力学参数，可以使额定转速下部件的工作频率避开结构的固有频率，从而有效减少机器的振动损伤，使机器的可靠程度大大增加。