基坑开挖对临近既有单桩承载性能的影响研究

何烈民 HE Lie-min；耿博光 GENG Bo-guang；王思瑞 WANG Si-rui

（①山东省路桥集团有限公司，济南 250014；②山东大学，济南 250061）

0 引言

基坑开挖产生的影响大致有三个方面：地下连续墙的变形、坑底隆起和基坑附近地表沉降。地下连续墙的侧移还会使基坑底部得土体发生隆起现象[1][2]。当基坑开挖时，由于基坑上方土体被挖出，原有的土体的自重应力消失，因此基坑底部土体会隆起[3]。坑外土体沉降发生之后，桩侧阻力受到影响，导致桩身轴力也将发生变化，影响到桩基的承载能力[4]。本文采用数值模拟进行基坑开挖对临近既有单桩承载性能的影响研究。

1 开挖问题的实现

1.1 ABAQUS中的单元生死功能

ABAQUS能够在分析步中将单元移除，并且自动计算单元节点力，随着单元的移除，使节点力逐渐减少直至为零，当移除分析步全部结束后，移除掉的单元对整个模型的影响就全部消失[5]。本文通过该功能来模拟基坑开挖工况。

1.2 初始应力场的建立

岩土工程中碰到的开挖问题,基本上就是隧道开挖与基坑开挖两种类型，而本文所涉及到的问题是基坑开挖问题,在实际工况中较为复杂，很难有具体的方法来完美分析开挖过程，往往需要用有限元分析软件来对此问题有一个具体分析。初始应力场的建立十分重要，影响着整个数据模拟过程，因此，如何能够平衡地应力是首先要考虑到的问题。

真实情况的土体应力极其复杂，很难具体模拟出应力的真实情况，本文通过施加边界条件和重力荷载模拟地应力的分布[6]，建立与工况大致相同的模型。

2 数值模拟过程

2.1 模型建立及参数选取

选取模型中包括三个部分，分别是土体，地下连续墙，桩体。土体模型选取为90m*90m*40m。基坑为30m*30m*8m，分为四次开挖，每次开挖2m。地下连续墙设置为厚度0.5m，埋深20m。桩半径为0.5m，桩长20m。土体采用Mohr-Coulomb理想弹塑性本构模型，泊松比取0.35，重度取18kN/m3，初始孔隙比取0.8，单位压力下土体孔隙比取1.5，回弹指数取0.008，压缩指数取0.037，临界状态应力比取1。地下连续墙，桩体采用线弹性本构模型，重度统一取25kN/m3，弹性模量统一取30GPa，泊松比统一取0.30。

2.2 材料接触及网格划分

在本次数值模拟中建立的模型中，桩底与土体的接触采用tie绑定，桩体的侧身与土体定义接触时，采用Penalty函数模型，摩擦系数设置为0.35。假设地下连续墙在基坑未开挖时就已经存在。地下连续墙与土体之间采用tie绑定，保证土体与地下连续墙之间在开挖之前已经绑定在一起，在开挖进行时，地下连续墙与土体之间具有相同的自由度。

对桩基划分网格前首先要进行种子布置，在桩周按照数量撒种子，种子数量为三个。网格划分采用六面体单元，控制属性为Structure。

2.3 荷载和边界条件

土体模型上方为自由表面，因此不受到约束。模型左右方向受到X方向的约束，即选择约束U1。模型前后方向受到Y方向的约束，即选择约束U2，模型下方受到XYZ三个方向的约束，即选择约束U1、U2、U3[5]。在地应力平衡步对整个模型施加大小为19kN/m3的体力，模拟出模型在重力作用下的性状。本文在各物理参数的基础上，确定在桩基的顶部施加的荷载为5MPa较为合适。

图1为单桩在基坑无开挖情况下的沉降量云图，桩顶沉降量10mm，桩底沉降量8mm，大体符合实际情况，证明桩顶施加荷载合理。

3 数值模拟结果分析

3.1 地应力平衡

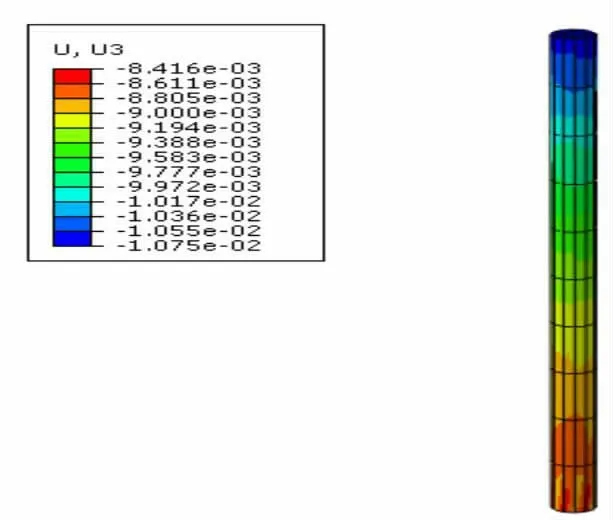
图1单桩沉降量云图

图2 与图3分别为地应力平衡完后的竖向位移与竖向应力云图。

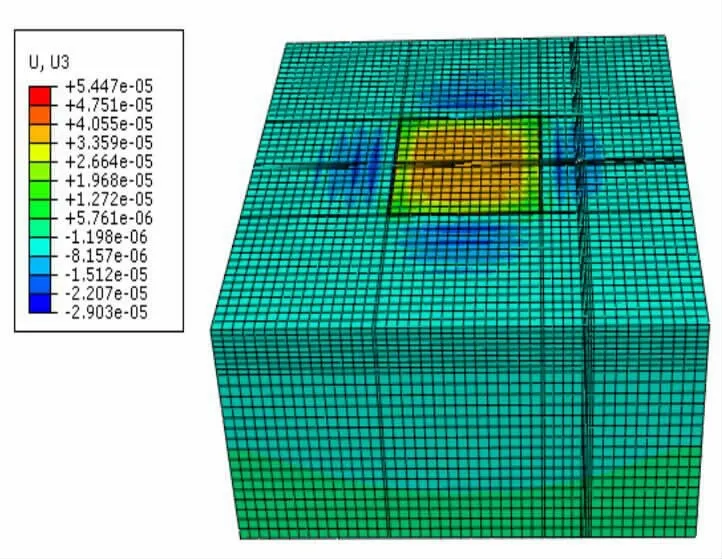
图2 土体竖向位移

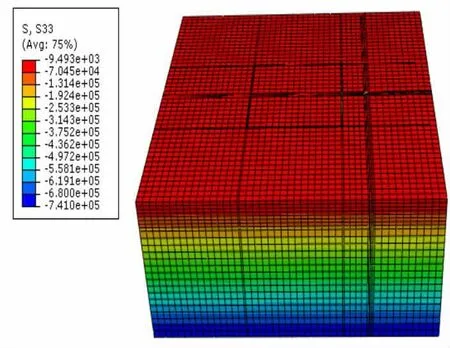
图3 土体竖向应力

由图2和图3可知，地应力平衡后土体的竖向位移的数量级为10-5m，应力的数量级为103N。初始应力与初始位移均比较小，基本与实际相符。

3.2 基坑开挖深度对邻近桩基的影响

本次开挖过程共计分为四次，每次2m，开挖深度H取值分别为2m、4m、6m、8m通过改变H值来确定基坑开挖对邻近建筑桩基的影响。不同开挖深度时桩的水平位移见图4。

图4 不同开挖深度时桩的水平位移

由图4可知，桩基在基坑开挖过程中，当开挖深度为2m时，桩的侧移最小，且随着桩的埋深不断减小，最大值在桩的顶部，为3mm左右。随着基坑的不断开挖，桩的侧移不断增大，当基坑开挖到8m时，桩的侧移最大值在桩的顶部，侧移量为19mm，且随着桩的埋深不断减少，但桩整体侧移变化量不大。

不同开挖深度桩的侧摩阻力变化见图5。

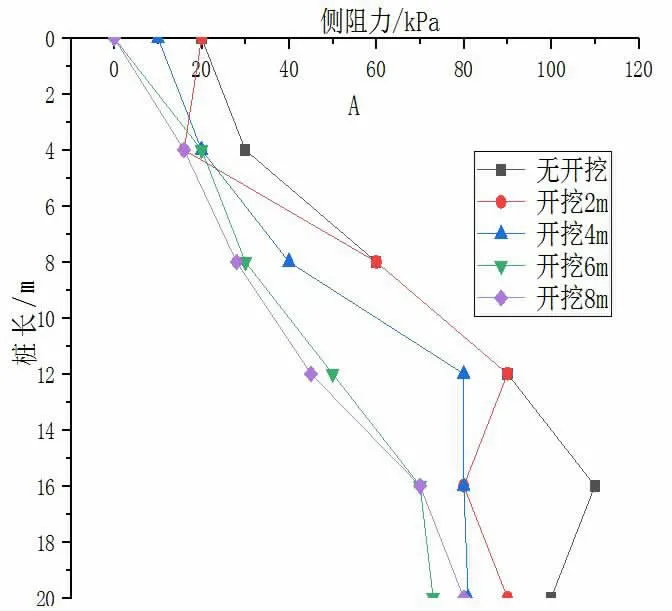
图5 不同开挖深度桩的侧摩阻力变化

由图5可知，伴随着土体的开挖，基坑周围土体发生变形，从而影响到桩的侧摩阻力，且开挖深度越大，开挖后基坑周围土体变形越大，对桩的侧摩阻力影响就越大。当无开挖时，桩的最大侧摩阻力为110kPa，随着开挖的的进行，最大侧摩阻力分别减少到90kPa、80kPa、70kPa、80kPa。且最大侧摩阻力均出现在桩的下部。

基坑开挖深度对桩基弯矩的影响见图6。

由图6可知，基坑周围土体随基坑开挖而发生沉降和水平变形，进而导致桩基周围土体也将发生位移，桩体两侧土体性质变得有所不同，在周围土体的作用下，桩要产生向基坑的弯矩[6]。随着基坑开挖深度的增加，桩身的弯矩也不断增加。当基坑开挖深度固定时，桩身的附加弯矩变化变化规律大体是桩顶与桩底较小，桩身中部较大，且弯矩最大值出现在中部。

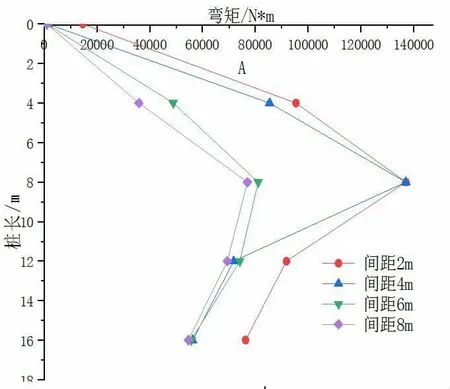
图6 弯矩随桩埋深的变化

3.3 桩与基坑的距离对桩基性能的影响

本文将通过设置四种工况，使桩基分别距离基坑2m、4m、6m、8m。基坑开挖深度8m，通过桩的侧移、侧摩阻力、弯矩等来研究桩基的性能。不同间距时桩的水平位移见图7。

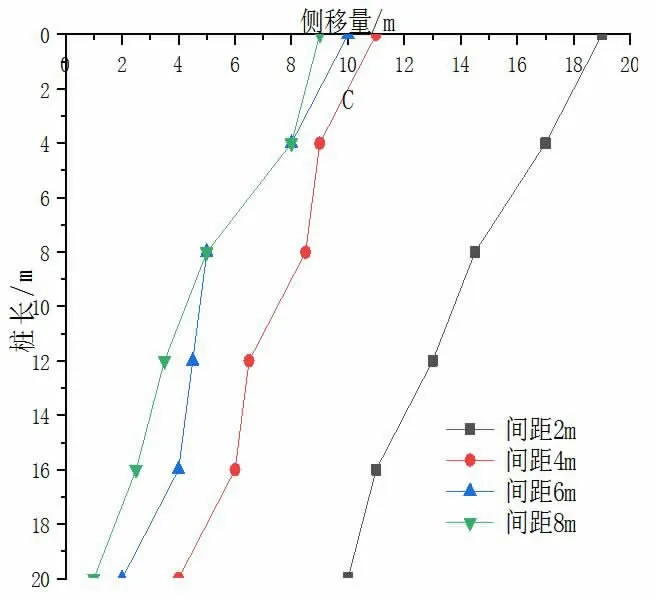
图7 不同间距桩的水平位移

由图7可知，当桩与基坑距离为2m时，桩的侧移量最小，随着距离的增大，基坑对桩侧移的影响越来越小，当桩与基坑距离在6m和8m时，侧移量均小于10mm，此时基坑对桩侧移量的影响可以忽略不计。

图8为开挖深度8m时桩基与基坑的距离对侧摩阻力的影响。

由图8可知，随着桩与基坑距离的增大，在同等埋深的桩体的侧摩阻力均有所增加。这是由于桩与基坑的距离变大，基坑开挖对桩基周围的土体影响变小，使桩周围的土体越来越接近无基坑开挖时的状态。

图8 不同间距桩的侧摩阻力变化

开挖深度为8m时桩基与基坑的距离对桩基弯矩的影响见图9。

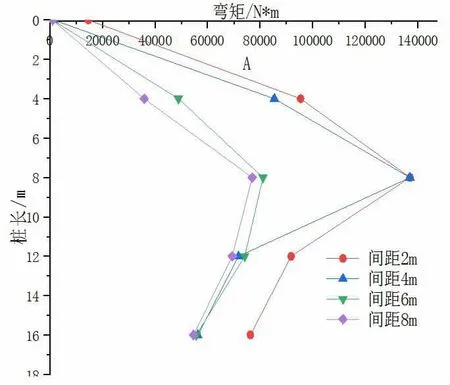
图9 不同间距桩的弯矩变化

由图9可知，桩体在远离基坑的过程中，桩体周围土体受基坑的影响越来越小，因此桩体的弯矩也在随着距离的增大而不断变小。桩身的附加弯矩在桩顶与桩底较小，桩身中部较大，且弯矩最大值出现在中部。

4 结论

采用数值模拟研究基坑开挖对单桩的影响，分析了单桩在受到开挖深度和距离基坑距离影响下的承载特性和变形规律。研究表明，基坑开挖越深，对桩的承载性能和变形影响就越大。桩与基坑开挖的距离越大，对桩的承载性能和变形影响越小。