长江经济带工业绿色发展效率测度——基于考虑指标偏好的广义DEA模型

陶硕 TAO Shuo

（重庆师范大学经济与管理学院，重庆 401331）

0 引言

党的十九大报告提出“加快生态文明体制改革，建设美丽中国”，强调人与自然是命运的共同体，制定优先重视保护的方针，并制定节约资源和保护环境的产业结构和生产方法。1999年，戴星翼[1]在《走向绿色的发展中》一书中首次明确提出“绿色发展”一词，从整个社会经济层面，讨论经济的可持续性发展（即绿色经济发展）问题。

工业作为国民经济支柱，工业绿色发展对于推动我国经济高质量发展具有重大意义。近几年来，不少学者开始对工业绿色发展效率进行了研究。在研究方法上，大多数学者采用数据包络分析方法[2]（Data Envelopment Analysis,DEA），DEA方法是一种评价多投入多产出的决策单元相对效率的非参数方法，是一种相对客观、科学的计算方法，是目前最常用的测度工业绿色发展效率的模型。吴旭晓[3]基于2005-2013年省级面板数据，运用超效率DEA视窗分析方法测算了青海、河南和福建的工业绿色效率。黄磊等人[4]采用考虑非期望产出的全局超效率SBM模型及泰尔指数分析2011-2016年长江经济带城市工业绿色发展效率的时空演变规律。王建民等人[5]基于长江经济带2007-2016年11省市面板数据，运用Super-SBM模型与Malmquist指数对工业绿色发展效率进行动静分析。丁显有等人[6]采用基于非期望产出的SBM-DDF模型测度了长三角城市群18个重要城市的绿色发展效率、创新发展效率。

传统的DEA方法通常以相同的目标、任务、外部环境和投入产出指标来评价决策单元。评价的参考框架默认为有效DMUs，没有提供独立选择评价标准的自由度。实际上，决策者可能需要根据需求选择合适的参照集。参考框架不仅是有效的决策单元本身，而且是一般单位、较差单位或特定单位。比如，低效DMU中的决策者可能希望将DMU与一些他们能够在短时间内匹配的适当样本单元进行比较，而不是与高效DMU进行比较。因此，马占新[7]开发了一组具有广义参考集的DEA模型，称作广义DEA模型，让决策者根据需求选择合适的样本单元。

考虑到在绿色发展效率评价中，决策者对某些评价指标有明显的偏好，并且需要自主选择评价参考系，因此，本文选择指标偏好顺序作为指标权重约束形式[8]，将决策者对指标权重偏好纳入到广义DEA模型中，构建了带权重偏好的广义DEA模型，将其应用于中国长江经济带工业绿色发展效率测度。

1 考虑指标偏好的广义DEA模型

1.1 广义DEA

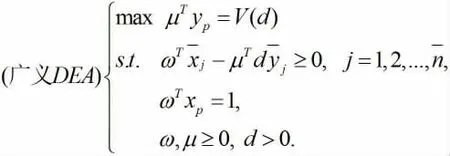
其中，xp=（x1p，x2p，…，xmp）T表示DMUp的投入指标向量，yp=（y1p，y2p，…，ysp）T表示DMUp的产出指标向量，=表示SUj的投入指标向量）T表示SUj的产出指标向量，ω=（ω1，ω2，…，ωm）T表示投入指标权重向量，μ=（μ1，μ2，…，μs）T表示产出指标权重向量，d是一个移动因子。

1.2 考虑指标偏好的广义DEA模型

本节将权重偏好引入广义DEA模型，构建了考虑指标偏好的广义DEA模型（Generalized DEA with Indicator Preference，GDEA-IP）。假设有n个DMU和个样本单位。DMU和样本单元的特征可以用m种投入和s种产出来表示。对于GDEA-IP（d）模型表示如下：

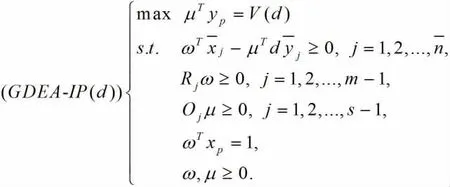
其中，R为投入的指标偏好矩阵，O为产出的指标偏好矩阵，Rj为R的第j行，Oj为O的第j行。GDEA-IP（d）给出了带有移动因子d的GDEA-IP模型。本文设d=1。

GDEA-IP模型的算法包括以下五个步骤。

步骤1：确定DMU的m种投入，s种产出。

步骤2：确定样本单元的m种投入，s种产出。

步骤3：根据定义1和定义2，确定投入指标偏好矩阵O和产出偏好矩阵R。

步骤4：解线性规划。

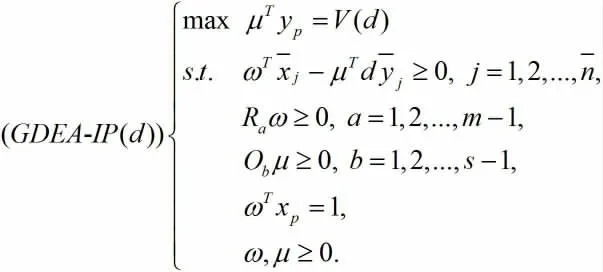
步骤5：根据效率值V（d）对所有DMU进行排序。

定义1：对于DMUp（p=1，2，…，n），设V（d）为GDEAIP（d）的最优值。如果V（d）≥1，则称DMUp相对于样本数据前沿面的d倍移动为弱GDEA-IP有效。

定义2：对于DMUp（p=1，2，…，n），设V（d）为GDEAIP（d）的最优值，ω0和μ0为GDEA-IP（d）的最优解。如果ω0＞0，μ0＞0且V（d）=1或者V（d）＞1，则称DMUp相对于样本数据前沿面的d倍移动为强GDEA-IP有效。

定义3：对于DMUp（p=1，2，…，n），设V（d）为GDEAIP（d）的最优值。如果V（d）＜1，则称DMUp相对于样本数据前沿面的d倍移动为GDEA-IP无效。

定理：DMU的GDEA-IP有效性与评价指标的量纲选择无关。

2 考虑指标偏好的广义DEA模型在长江经济带工业绿色发展效率中的应用

本节采用广义DEA模型和GDEA-IP模型对2016年中国长江经济带11个地区的工业绿色发展效率进行测算和排序。

2.1 指标和数据

工业绿色发展效率评价指标包括三种投入指标：资本投入、能源投入和劳动力投入；三种产出指标：一个期望产出和两个非期望产出。评价指标和数据分别如表1和表2所示，其中非期望产出已通过INP方法进行处理。实证研究的数据来自《2017年中国工业统计年鉴》、《2017年中国城市统计年鉴》、《2017年上海统计年鉴》、《2017年江苏统计年鉴》、《2017年浙江统计年鉴》、《2017年安徽统计年鉴》、《2017年江西统计年鉴》、《2017年湖北统计年鉴》、《2017湖南统计年鉴》。选取中国长江经济带11个地区作为DMU1-DMU11。这11个地区分别是上海市、江苏省、浙江省、安徽省、江西省、湖北省、湖南省、重庆市、四川省、贵州省和云南省。

表1 投入产出指标

表2 实证研究数据

2.2 结果分析

通过专家评估得，投入指标偏好关系为ω1≥ω2≥ω3，产出指标偏好关系为μ1≥μ2≥μ3。则权重约束矩阵，

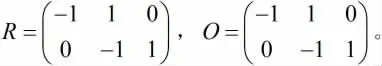
本章广义DEA模型和考虑指标偏好的广义DEA模型的算法通过MATLAB软件编程实现。

首先运用GDEA-IP模型（样本单元选取为所有决策单元）计算出11个省市的工业绿色发展效率值，结果如表3所示。

表3 基于GDEA-IP模型的效率值

将长江经济带11个省市进一步划分为“东部地区”（DMU1，DMU2，DMU3）、“中 部 地 区”（DMU4，DMU5，DMU6，DMU7）、“西部地区”（DMU8，DMU9，DMU10，DMU11）。计算出每一类地区工业绿色发展效率值的平均值，结果如表4所示。

表4 三类地区的效率平均值

由表4可得，东部地区的效率值的平均值最大，表明东部地区工业绿色发展总体最好，因此选择东部地区的三个省市作为GDEA-IP模型的样本单元，进行效率值的进一步测算。表5给出了基于广义DEA模型和GDEA-IP模型的效率和排名，其中，DMU1、DMU2和DMU3作为样本单位。

表5 基于广义DEA模型和GDEA-IP模型的效率值和排序

由表5可知，将权重偏好引入广义DEA后，54.5%的决策单元的效率值发生了变化，其中DMU11效率值的变化最为明显，从2.47下降到0.85，从广义DEA有效变化为GDEA-IP无效。72.7%的决策单元的排名发生了变化，其中原本排名第三名的DMU5上升为第一名，而原本排名第一名的DMU11大幅度下降到第九名。

然而，GDEA-IP得到的排名完全合理吗？对此，我们选取DMU8，DMU10，DMU11的投入产出数据及效率计算结果进行比较分析，如表6所示。

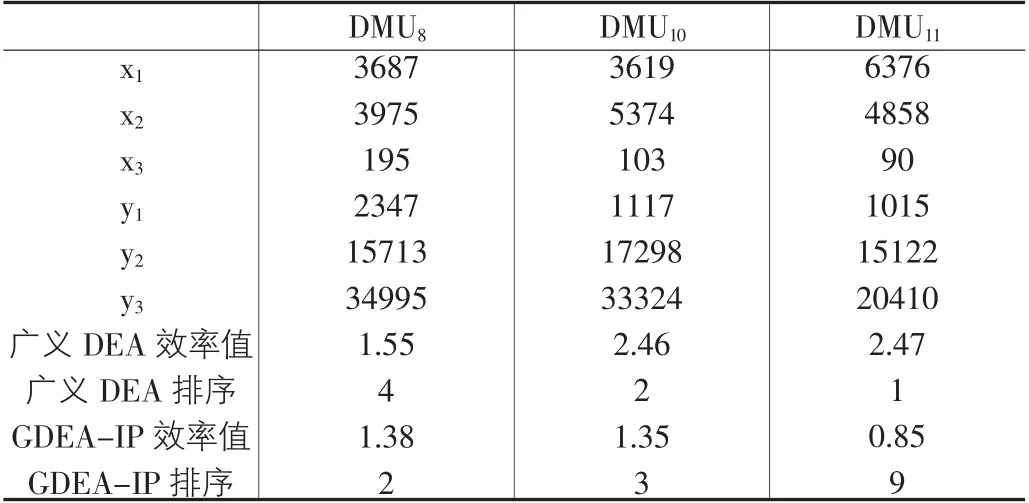
表6 对比分析结果

首先将DMU8和DMU11对比分析。从投入指标的数值上 看，x1（DMU8）＜x1（DMU11），x2（DMU8）＜x2（DMU11），x3（DMU8）＞x3（DMU11）。由于事先约束了x3的权重最小，因此x3对最终效率值的影响最小；从产出指标的数值上看，y1（DMU8）＞y1（DMU11），y2（DMU8）＞y2（DMU11），y3（DMU8）＞y3（DMU11）。根据“投入越少，产出越多的单元效率值越高”的原则，直观上可看出，DMU8的效率值应该大于DMU11的效率值。广义DEA模型的计算结果刚好相反，而GDEAIP模型的计算结果是合理的，符合人们的直观评价。

接着将DMU10和DMU11对比分析。从投入指标的数值上看，x1（DMU10）＜x1（DMU11），x2（DMU10）＞x2（DMU11），x3（DMU10）＞x3（DMU11），并且x1（DMU10）远远小于x1（DMU11），减小幅度高达76%，虽然x2（DMU10）大于x2（DMU11），x3（DMU10）大于x3（DMU11），但增加的幅度均小于15%，并且事先约束了x2和x3的权重较小，因此x2和x3对最终效率值的影响较小；从产出指标的数值上看，y1（DMU10）＞y1（DMU11），y2（DMU10）＞y2（DMU11），y3（DMU10）＞y3（DMU11）。同理，根据“投入越少，产出越多的单元效率值越高”的原则，从直观上可得DMU10的效率值应该大于DMU11的效率值，这与广义DEA模型的计算结果相反，与考虑权重约束的广义DEA模型的计算结果相同。

对比分析表明，如果不考虑权重偏好，广义DEA方法可能会导致不合理的结果，而GDEA-IP模型计算的排序结果更合理，更符合人们的直观评价。

综上所述，GDEA-IP不仅可以考虑投入和产出指标的重要程度，而且可以对所有DMU进行全面排序。可见，没有权重约束的DEA模型是存在缺陷的，只有充分考虑评价指标之间相互影响而客观存在的共同逻辑关系，并将其纳入DEA模型的约束条件才能获得更科学更合理的结论。

因此，通过分析表5的GDEA-IP模型效率值可得如下结果。从整体来看，长江经济带工业绿色发展效率的平均值为1.07，处于DEA有效水平，表明整体效率较高。从东中西部地区来看，三个地区的平均效率值差距相对较小，地区差异不明显。从每一类地区的内部来看，东部地区的上海市和江苏省为DEA有效，东部地区内部三个省市效率值差异很小，最大效率值与最小效率值仅仅相差0.05；中部地区的江西和湖南为DEA有效，中部地区内部四个省市效率值差异很大，最大效率值与最小效率值相差高达1.01；西部地区的重庆和贵州为DEA有效，西部地区内部四个省市效率值差异较大，最大效率值与最小效率值相差0.85。

3 结论

通过构建考虑指标约束的广义DEA模型，对中国长江经济带工业绿色发展效率进行分析，得到以下结论：①从整体来看，长江经济带工业绿色发展水平较好，整体效率较高，处于DEA有效水平。②分地区来看，东中西三个地区的平均效率值差距相对较小，地区差异不明显。③从地区内部来看，东部地区内部省市效率值差异很小；中部地区内部省市效率值差异很大；西部地区内部省市效率值差异较大。表明中西部地区发展不均衡、不稳定，政府需采取措施积极推进中西部地区工业绿色转型，构建协同发展机制，促使各地区协同发展。