基于风险梯度的化工企业事故风险定量评估*
胡 涛,曹日红,闫 放,汪长松,黄 锐,李孜军
(中南大学 资源与安全工程学院,湖南 长沙 410083)
0 引言
化工园区中的企业多为化工石化企业,这些企业生产、储存、使用着大量易燃易爆、有毒的危险化学品,一旦发生事故,极易造成大面积的群死群伤[1]。因此,有必要对这些企业进行风险评估,分析其危害特性从而完善相应的安全措施,减少事故损失,本文将以风险场理论为基础来对此展开研究分析。风险场理论是以场论为基础的三维风险分析理论,它通过构建出风险的三维数量场函数来展示危险源在空间的风险分布,并以风险梯度来描述风险的变化情况,从而研究事故的风险传播效应[2],现已在化工、交通、环境等多个领域得到初步应用。如邢永健等[3]分析了风险场对风险受体的作用机制,构建了南京化工园区内各风险源所产生的环境风险场,并进一步对环境风险受体进行分析得到了相应的区域环境风险水平分布情况;王建强等[4]基于风险场理论建立了人-车-路闭环系统的行车风险场模型,为复杂环境下行车风险评估和车辆主动控制提供了新的判决依据。但总的来说,风险场理论仍需进一步的发展完善,考虑到诸多文献提及风险场理论中的风险梯度概念[2,5-6],而关于如何将其进一步应用于事故风险评估中却鲜有报道,因此,以某区域内存在的2家化工企业为例,利用风险场理论对其进行事故风险分析,并基于风险梯度来展开进一步的研究与应用。
1 方法介绍
首先,需要构建出评估案例的风险值计算公式,这里采用频率与严重度相乘的形式[7],如式(1)所示:
Fi(x,y,z)=εifiSi(x,y,z)
(1)
式中:Fi(x,y,z)为风险类型为i时的风险值;εi为安全措施导致的风险补偿系数;fi为频率;Si(x,y,z)为严重度。
若评价目标内存在多个危险源,应进行叠加计算,计算公式如式(2)所示:
(2)
式中:Fi,s(x,y,z)表示叠加后的总风险值;n表示危险源数目。
在风险值计算公式的基础上求偏导,可以得到风险梯度的计算公式,如式(3)所示。风险梯度描述的是风险在空间的变化情况。
(3)

在求得风险梯度后,可引入最速下降法来求得最优的风险降低路径。假设风险值如式(1)计算,引入式(4)计算风险负梯度,计算公式如下所示:
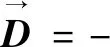
(4)
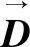
(5)
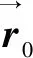
(6)
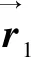
(7)

2 案例分析
2.1 企业概况
图1、图2分别是评估区域内2家企业的平面图。其中图1(甲企业)为1家氮肥企业,主要危险源为储存在A1,D1 2处的液氨,图2(乙企业)为1家煤化工企业,主要危险源为储存在B2,E2 2处的甲醇。由于计算方法相近,本文先以甲企业为例来说明分析与计算的过程。
2.2 事故风险辨识与分析
液氨属于危化品,一旦发生泄漏,氨气的易燃、易爆与有毒特性可能会导致火灾、爆炸与中毒事故的发生[8]。在这3类事故风险中,氨气中毒的风险大小由毒物浓度决定,因此需要计算氨气在某点的浓度。假设液氨发生的是连续型泄漏,则可由式(8)来计算液氨的泄漏速率[9],计算公式如下:
(8)
式中:Q是泄漏速率,kg/s;Cdg是泄漏系数,取1.00;A是泄漏面积,m2;P为储罐内压力,Pa;M为气体分子量,取0.017 kg/mL;R是气体常数,取8.314 J/(mol·K);k是绝热指数(等压比热容与等容比热容的比值),取1.310;T为气体绝对温度,K。
采用高斯烟羽模型来计算氨气在某点的浓度[10]。为简化计算,假设液氨从地面泄漏(即H=0),可得到液氨从地面泄漏时的浓度计算公式,如式(9)所示:
(9)
式中:C(x,y,z)为危险物质从地面泄漏时气云中危险物质的浓度,kg/m3;π为常数;Q为连续泄漏速率,mg/s;μ为风速,m/s;σy,σz为y和z方向上的扩散系数,m;z为浓度测量点高度,m;x,y为观察对象距离液氨储罐的下风向和横风向距离,m。
火灾对人的风险表现为热辐射,假设这里火灾类型为喷射火,则可以用式(10)进行计算[11]:
(10)
式中:I(x,y,z)为热辐射强度,W/m2;ηj为效率因子(取值由式(11)确定[11]),Hc为燃烧热,J/kg;Q是泄漏速率,kg/s;Tjet为辐射系数;d为评价点位置与着火点位置的距离,m。
(11)
式中:Ps为饱和蒸气压,MPa。
爆炸对人的风险表现为超压,计算方法如式(12)~(14)所示[12]:
(12)
式中:mTNT为等效TNT质量,kg;md为发生爆炸的气体的量,kg;ΔHd为爆炸气体的燃烧热,kJ/kg;QTNT为TNT的燃烧热,取 4 601 kJ/kg。
(13)
式中:ZG与RG分别为评价点位置距离爆炸点位置的尺度距离与实际距离,m。
(14)
式中:Po为超压,Pa。
2.3 风险函数与风险梯度函数的计算
化学中毒、热辐射以及超压是不同的风险类型,不能够直接叠加计算,因此需要对其进行归一化处理,归一化处理的原则依据这3类风险对人体的损坏程度。由文献可知上述3类风险能对人体造成伤害的最小值分别为:30 mg/m3、1.6 kW/m2、20 kPa;造成人体死亡时所对应的值分别为:3 500 mg/m3、37.5 kW/m2、50 kPa。选取各类风险中伤害后果为“死亡”时所对应的值作为其严重度的最大值,以此来进行归一化处理,得到各类风险的严重度,分别如式(15)~(17)所示:
(15)
式中:SCP(x,y,z)为人中毒时候的严重度;C(x,y,z)为危险物质从地面泄漏时气云中危险物质的浓度,mg/m3。
(16)
式中:STR(x,y,z)为人在遭受热辐射时候的严重程度;I(x,y,z)为热辐射强度,W/m2。
(17)
式中:SOP(x,y,z)为人在遭受超压时的严重度;Po(x,y,z)为超压,Pa。
同时考虑A1,D1 2处的液氨泄漏事故的影响,并依据前文设定得到引发事故的2个危险源的坐标为(30,132,0)和(191,140,0),假设事发时大气稳定度等级为C(即σy=0.22x(1+0.000 4x)-1/2,σz=0.20x)[14],主要风向沿x轴正方向,其它相关计算参数如表1所示。

表1 甲企业计算参数取值Table 1 Values of calculation parameters of enterprise A
根据实际情况,将风险补偿系数设为0.6,氨气中毒事故发生的频率为2.548×10-1次/a,火灾与爆炸事故的频率分别为2.885×10-2,1.442×10-2次/a。最终可得到液氨的风险值计算公式,如式(18)所示:
(18)
式中:F甲(x,y,z)表示甲企业中观测点的风险值;f1=(x-30)2+(y-132)2+z2;f2=(x-191)2+(y-140)2+z2;x,y,z为观测点的三维空间坐标。
同理,可以得到乙企业所对应的风险值计算公式(由于甲醇沸点高,挥发能力有限,故这里不考虑其毒理性质)。先计算出乙企业中B1,E1 2处甲醇的泄漏流量,计算公式如式(19)所示[15]:
(19)
式中:Q为物质的泄漏速率,kg/s;CD是泄漏系数,取0.61;Ah是泄漏面积,m2;k是绝热指数,取1.2;p为储罐内的压力,Pa;ρ为密度,kg/m3。
再以同样方法计算出乙企业中的事故严重度,相关计算参数如表2所示。

表2 乙企业计算参数取值Table 2 Values of calculation parameters of enterprise B
根据实际情况,得知2危险源坐标为(65,90,3)和(76,140,5),风险系数设置为0.5,火灾与爆炸事故的频率分别为1.2×10-1次/a、1.6×10-3次/a,最终得到乙企业的风险值计算公式如式(20)所示:
(20)
式中:F乙(x,y,z)表示乙企业观测点的风险值;f3=(x-65)2+(y-90)2+(z-3)2;f4=(x-76)2+(y-140)2+(z-5)2;x、y、z为观测点的三维空间坐标。
表3和表4是依据前文设定以及公式(1)所得到的甲、乙2企业的风险阈值区间。

表3 甲企业风险阈值划分Table 3 Classification of risk thresholds of enterprise A
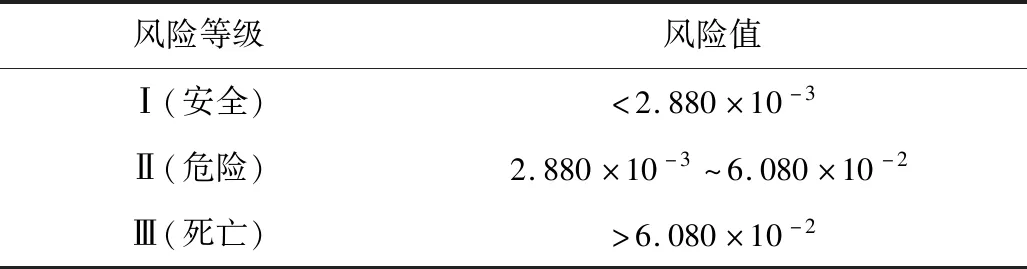
表4 乙企业风险阈值划分Table 4 Classification of risk thresholds of enterprise B
2.4 风险评估结果分析
空间中风险值相等的点所构成的曲面称为风险等值面[16]。基于表3和表4生成甲、乙2企业的风险等值面三维图,如图3和图4所示。
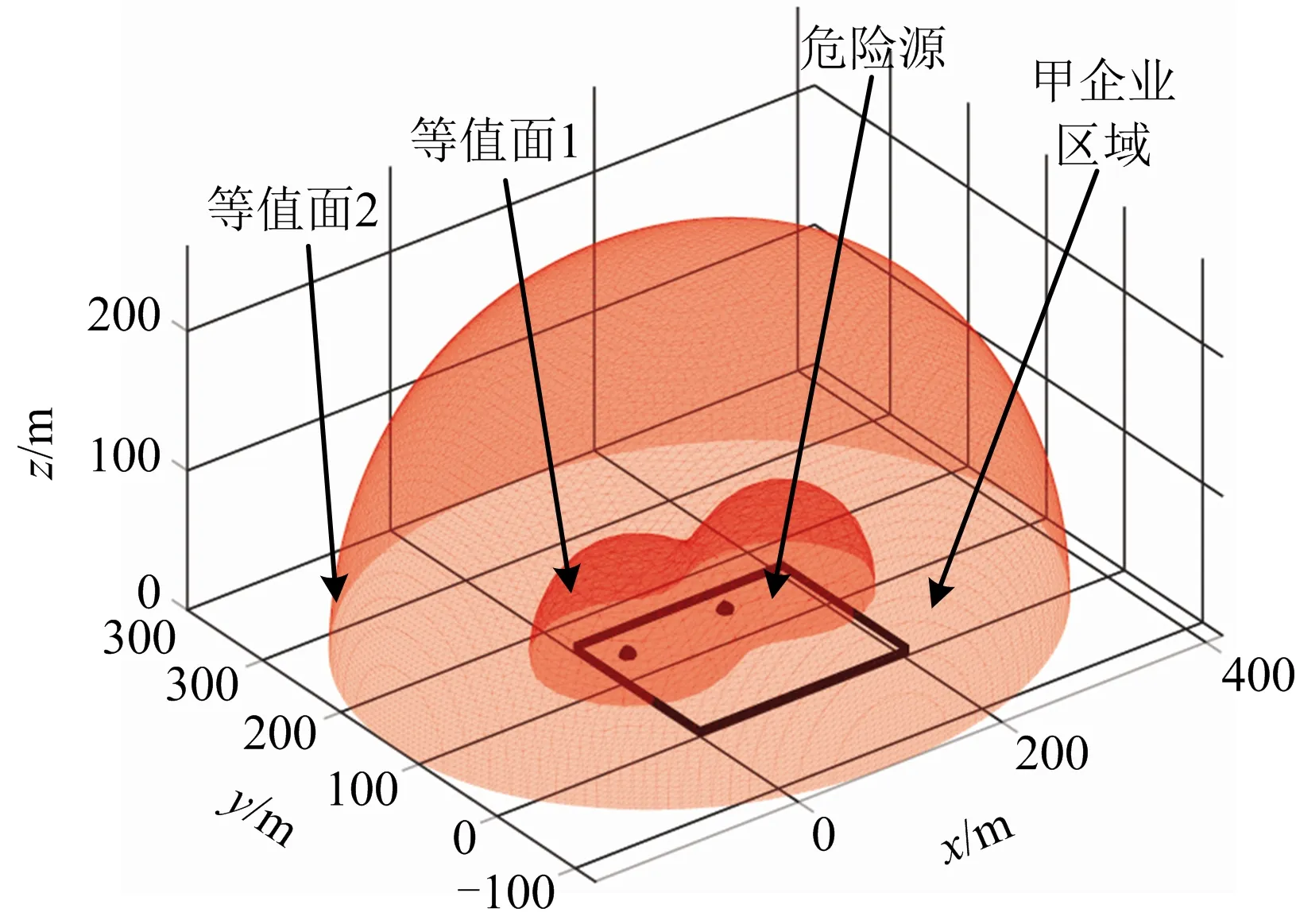
图3 甲企业风险等值面Fig.3 Risk isosurface of enterprise A

图4 乙企业风险等值面Fig.4 Risk isosurface of enterprise B
当人位于等值面1或等值面3内部时,即甲企业风险值大于1.787×10-1或乙企业风险值大于6.08×10-2时,为Ⅲ级风险,会遭遇死亡危险;而当人位于等值面2或等值面4外部时,即甲企业风险值小于2.599×10-2或乙企业风险值小于2.88×10-3时,为Ⅰ级风险,可认为其不会受到事故影响;其余部分为Ⅱ级风险。考虑到企业实际人口分布情况(先以甲企业为例),选取企业中人数最多的5个位置作为观察点,将其坐标(W11(35,70)、W21(70,75)、W31(70,125)、W41(130,120)、W51(155,45))带入式(18)中计算其风险值(z值均取1.5),分别为2.736×10-1、2.358×10-1、6.925×10-1、2.879×10-1、1.148×10-1,风险值均高于2.599×10-2,一旦发生事故,人员就需要及时进行疏散。因此,可在风险负梯度的基础上引入最速下降法来搜寻最优风险降低路径。首先,通过对甲企业风险值计算公式求偏导得到相应的风险梯度公式,然后以上述5个观测点的位置作为初始位置,将2.599×10-2设置为目标风险值,步长设置为400,经过多次迭代计算,最终得到这5个位置所对应的最优风险降低路径,如图5中曲线①~⑤所示。等值线1、等值线2是由风险等值面1和风险等值面2从三维图形转化为二维图形所得(即令z取人体平均致命高度1.5 m且仅截取部分等值线进行展示)。从图5可知,当人从初始位置分别逃至与等值线1的交点处,即W12(35.413,53.082)、W22(75.794,63.530)、W32(116.071,81.950)、W42(117.788,81.754)时,风险值降为1.787×10-1,风险降至II级,当人进一步到达与等值线2交点处,即到达W13(3.277,-114.219)、W23(89.592,-125.579)、W33(136.701,-123.049)、W43(135.534,-102.3 28)、W52(180.412,-109.541)时,风险会降至I级,人员到达安全区域。
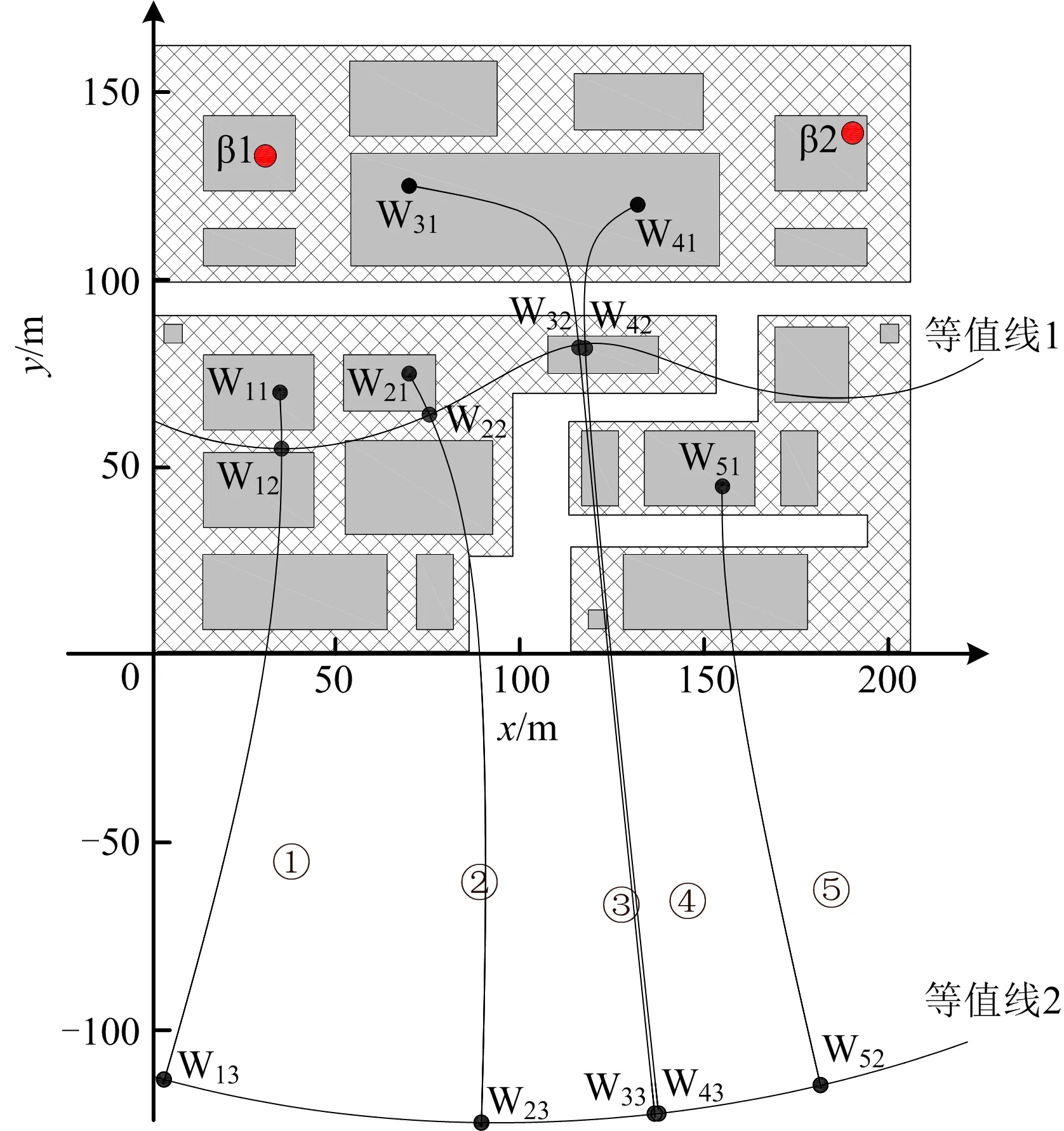
图5 甲企业最优风险降低路径Fig.5 Optimal path of risk reduction of enterprise A
同理,可得乙企业的最优风险降低路径,如图6中曲线⑥~⑩所示。等值线3、等值线4是由风险等值面3和风险等值面4从三维图形转化为二维图形所得(即令z取人体平均致命高度1.5 m且仅截取部分等值线进行展示)。从图6可知,当人从初始点(W61(40,20)、W71(80,50)、W81(130,30)、W91(110,90)、W01(180,130))分别逃至与等值线4的交点处,即到达点W62(14.470,-54.554)、W72(112.186,-57.207)、W82(175.703,-23.798)、W92(226.713,45.594)、W02(240.233,135.550)时,风险值会降至2.880×10-3,这时人已逃出危险区域。
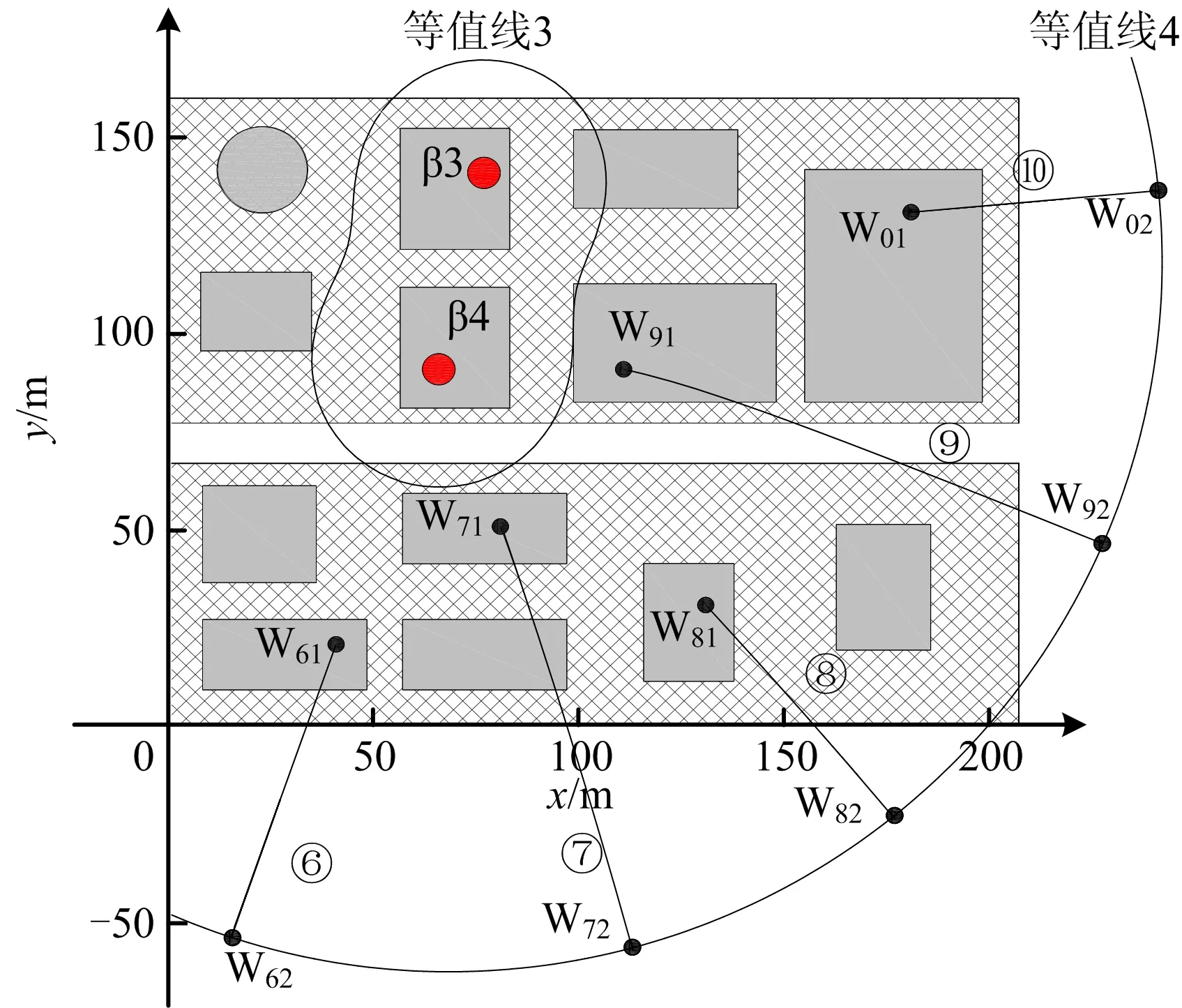
图6 乙企业最优风险降低路径Fig.6 Optimal path of risk reduction of enterprise B
需要注意的是,所求得的最优风险降低路径并不完全处在空旷的道路和平地上,它们还贯穿了一些存在建筑物或障碍物的区域,因此在实际应用当中还需根据现场情况进行适当调整。
3 结论
1)甲企业人员最多的的5个位置中,有4个位置属于Ⅲ级风险,其余1个位置属于Ⅱ级风险,而乙企业中人员最多的5个位置均为Ⅱ级风险,所以相比而言,乙企业的人员更有安全保障,人员分配更为合理。
2)基于甲企业所得的各级风险等值面所囊括体积要比基于乙企业所得的各级风险等值面体积更大,而且甲企业中III级风险区域的面积占甲企业总面积的比例较高,所以甲企业的事故总体风险比乙企业更大,更需要加强安全管理,妥善做好事故预防工作。
3)从最优风险降低路径来看,乙企业中的5条最优风险降低路径的里程更短,穿过的建筑物和障碍物也更少,若事故真实发生,乙企业在人员疏散方面将会更有优势。

