附加傅里叶补偿项的卫星遥感影像RFM平差方法

余俊鹏，吴伟东，孙佳明，满益云，沈 刚

1. 广东工业大学土木与交通工程学院，广东 广州 510006； 2. 钱学森空间技术实验室，北京 100094

有理函数模型(rational function model,RFM)自1999年作为商业遥感卫星IKONOS-2的影像定位模型推出后，因其通用性强、方便实用等优点，很快被广泛应用，成为卫星遥感影像处理的主要几何模型[1]。由于RFM本质上是遥感成像几何的一种数学拟合模型，受影像内外方位元素观测误差影响，RFM直接定位结果存在系统误差。为满足测图精度要求，学者们分别提出了RFM的像方平差和物方平差方案[2]。目前以像方平差方案较为常用[3]，该方案保持RFM模型参数(rational polynomial coefficients,RPC)不变，通过附加像方定位系统误差补偿项并对其进行平差求解，使影像定位精度显著提高[4-9]。

近年来，随着遥感卫星的数量和类型增多，RFM平差方法随之不断优化，以适应不同场景的数据处理需求。文献[10]针对弱交会条件下卫星遥感影像区域网平差无法正确求解的问题,通过引入数字高程模型作为高程约束，实现近似垂直观测影像的高精度平面定位。文献[11]利用同轨道长条带卫星影像的系统误差分布特性，提出基于轨道约束的区域网平差方法，减少了平差所需控制点。文献[12]对于大规模区域网平差问题，利用RPC生成虚拟控制点，并将其作为带权观测值引入平差模型，克服了在无控制点条件下平差精度不稳定的问题。文献[13]提出一种利用平均高程面的RFM区域网平差模型，改进了国产静止轨道遥感卫星高分四号影像的内部拼接精度。文献[14]提出采用三阶多项式进行像方系统误差补偿，提高了资源三号立体影像定位精度。

尽管RFM平差的实现方法因具体需求而异，但其平差模型都采用一般多项式作为附加项，对像方系统误差的补偿效果基本相同。而卫星传感器成像受到姿轨误差、平台颤振、大气折光、镜头畸变、焦面形变及内部拼接等各种因素影响[15-19]，实际的像方系统误差相当于一种复杂畸变。由于一般多项式理论上无法对整个像幅范围内的多种畸变进行精确拟合，在某些点位可能残存较大误差，导致定位结果的精度和可靠性降低。对此，本文根据傅里叶级数的逼近特性，提出一种可适应符合连续条件下任意形式畸变的RFM平差方法，并通过模拟和真实数据的平差试验，验证了该方法的可行性和有效性。

1 平差模型

1.1 RFM基本形式

RFM是星载传感器成像几何的一种通用数学表达式，将成像目标的像点坐标(R,C)表示为物方坐标(B,L,H)的多项式的比值，如式(1)所示

(1)

式中，(r,c)为正则化的像点坐标；(φ,λ,h)为正则化的物方坐标，物方坐标可取地心直角坐标、大地坐标或地图投影坐标。正则化公式为

(2)

式中，Roff、Rscale、Coff、Cscale为像方坐标的正则化参数；Boff、Bscale、Loff、Lscale、Hoff、Hscale为物方坐标的正则化参数。经正则化后，像方坐标和物方坐标数值范围为(-1.0～+1.0)，以减小两者转换计算误差。P1、P2、P3、P4均为一般多项式，最高不超过3次，形式为

Pi(φ,λ,h)=ai1+ai2λ+ai3φ+ai4h+ai5λφ+

ai6λh+ai7φh+ai8λ2+ai9φ2+

ai10h2+ai11φλh+ai12λ3+ai13λφ2+

ai14λh2+ai15λ2φ+ai16φ3+

ai17φh2+ai18λ2h+ai19φ2h+ai20h3

(3)

式中，aij(j=1,2,…，20)为多项式系数，即RPC参数，其中a21、a41取常数1。RPC参数通常由地形无关算法得到，即先利用影像定向元素构建严格成像几何模型，并在影像覆盖区域范围内生成虚拟控制格网，再根据大量均匀分布的虚拟控制点坐标求解RPC参数。

1.2 RFM平差模型

1.2.1 观测方程

受卫星影像定向元素观测值的误差影响，RFM像方定位结果存在系统误差。像点坐标观测值为

(4)

式中，(R′,C′)为利用RFM得到的像点坐标计算值；(ΔR,ΔC)为像方系统误差补偿项。理论上，(ΔR,ΔC)的函数形式越符合实际误差分布，其补偿效果越好，常规采用的一般多项式补偿项为[20-21]

(5)

式中，J为多项式阶数；ek、fk为多项式系数；p、q分别为各项中R、C的幂次数。二阶一般多项式如式(6)所示

(6)

而一阶一般多项式即为仿射变换式[22]为

(7)

大量试验表明，e0、f0可以分别吸收卫星沿飞行方向和垂直飞行方向的外方位元素及像主点偏移系统误差，e1、e2和f1、f2可吸收主距变化引起的误差。但对于影像中存在的复杂畸变，唯有寻求相适应的补偿函数才能进一步有效消除。

根据高等数学理论，傅里叶级数具有全局逼近特性，可趋近于二维区间内符合连续条件的任意函数[23]。由此可知，以二元傅里叶多项式作为像方系统误差补偿项，能够精确描述影像平面上存在的多种复杂畸变[24]，其形式为

(8)

(9)

(10)

式中，w为影像宽度；h为影像高度；M、N为阶数。傅里叶多项式阶数越高，对畸变的拟合精度越高。当M=N=1时，傅里叶补偿项简化为常数项

(11)

当M=N=2时，傅里叶补偿项含16个待求参数，形式为

(12)

当M=N=3时，傅里叶补偿项参数增加至36个，形式为

(13)

傅里叶补偿项参数之间严格正交，有利于平差求解。但多项式阶数过高仍可能产生过度参数化问题[25]，实际处理时应根据影像畸变复杂度及平差条件，选取合适的阶数以满足定位精度要求。

1.2.2 平差计算

在像点坐标观测方程中，设像方系统误差补偿项ΔR、ΔC分别包含c、d个补偿项系数，对式(4)线性化可得到光束法平差的误差方程为

(14)

将式(14)写成矩阵形式

V=At+Bx-l

(15)

式中，V为像点坐标观测值残差向量；t=[Δe0Δe1…Δec-1Δf0Δf1…Δfd-1]T为补偿项系数T的增量向量；x=[ΔBΔLΔH]T为目标点的物方空间坐标X的增量向量，对于控制点可令x=0；A、B为系数矩阵，即对未知数的偏导数矩阵；l=[R-R0C-C0]T为常数项，其中(R,C)为像点坐标观测值，(R0,C0)为利用未知数近似值代入式(4)计算得到的像点坐标。计算误差方程各项数值时，RFM补偿项系数初值T0设为0，各目标点的物方空间坐标初值X0通过基于RFM的立体定位方法逐点计算得到，具体计算过程参见文献[2]。

由式(15)根据最小二乘平差原理建立如下法方程，用于求解补偿项系数及待定目标点的物方坐标增量

(16)

平差求解需要迭代进行。第1次求解采用一阶多项式补偿项并更新RPC参数，随后可采用傅里叶补偿项逐步消除残余系统误差。在完成第s(s>1)次求解后，对未知数进行修正并将其作为下次求解的未知数初值，即Ts+1=Ts+t、Xs+1=Xs+x，再重新计算未知数增量t、x，直至平差过程收敛。

2 试验及结果分析

本文先通过仿真卫星影像数据，对附加傅里叶补偿项的RFM平差方法进行测试，验证新方法的畸变补偿性能，进而通过两组真实卫星影像数据的平差试验，比较新方法与常规方法的实际处理效果。

2.1 仿真试验

仿真数据以卫星遥感影像的成像几何模型为基础，按设定的卫星立体传感器成像参数及畸变模型参数构建物像几何关系，生成覆盖一定区域范围的地面点坐标及其像点坐标。对各项摄影测量模拟“真值”引入随机误差后作为待平差观测数据。具体仿真参数见表1。

表1 卫星立体遥感影像仿真参数Tab.1 Simulation parameters of satellite stereo remote sensing images

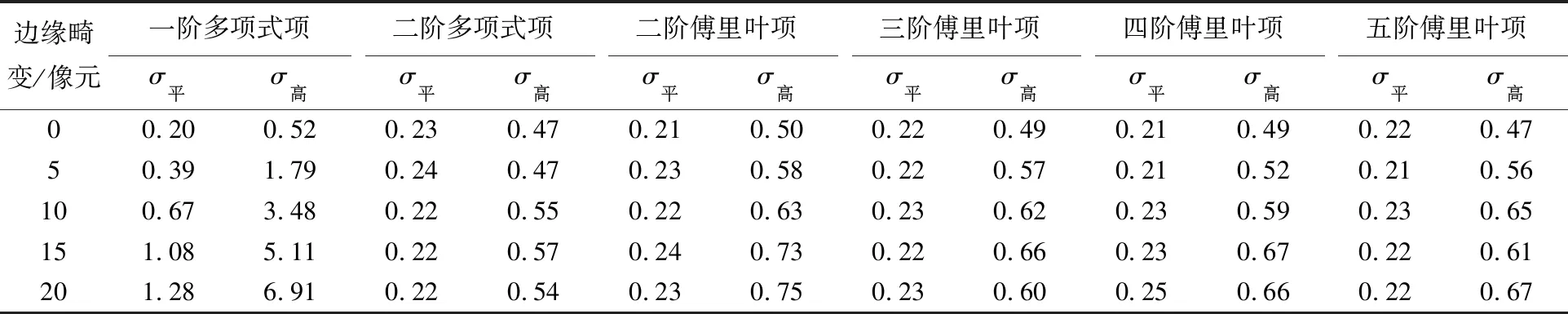
表2 对仿真数据用不同平差方法得到的物方定位精度Tab.2 Geopositioning accuracy results of simulation data obtained by different adjustment methods m

在无畸变情况下，像方定位系统误差完全由影像内外方位元素误差所致。采用一阶多项式补偿项进行平差后物方定位中误差从平面26.7 m、高程14.9 m分别减小为平面0.20 m、高程0.52 m，平面精度相当于像方0.25个像元大小，接近于像点观测精度0.2像元，说明一阶多项式对于消除影像内外方位元素的误差影响十分有效。本文方法与常规方法定位精度相当，表明傅里叶多项式也可以有效补偿影像内外方位元素误差造成的定位误差。

在引入二次模拟畸变后，从理论和试验结果看采用二阶多项式补偿项平差效果最优，因此可以以其作为其他补偿方法的评价基准。由表2看出，随着模拟畸变的增大，一阶多项式补偿效果呈现下降趋势。当影像边缘畸变为5像元时，物方定位中误差为平面0.39 m、高程1.79 m。定位中误差随畸变同步扩大，当畸变增大至20像元时，平差定位中误差为平面1.28 m、高程6.91 m，说明该方法无法完全消除二次畸变，且原畸变越大，平差后的残余系统误差也越大。当采用附加傅里叶补偿项的平差方法时，平面定位精度基本上不再受畸变大小影响，平差后均在0.3像元以内，接近像点观测精度水平。高程定位精度随畸变增大而缓慢下降，平差后保持在0.8 m即像元分辨率以内。以三阶傅里叶补偿项为例，在边缘畸变20像元的情况下，本文方法比常规方法的平面精度提高(1.28-0.23)/1.28≈82%，高程精度提高(6.91-0.60)/6.91≈91%，表明傅里叶补偿项对二次畸变的拟合补偿能力有显著提高，且接近于最优水平。

理论上，傅里叶多项式阶数越高，对畸变拟合补偿效果越好。但从仿真数据的平差结果看，采用过高的阶数对提高精度作用不大，反而可能因为过度参数化导致物方坐标求解精度下降。本文在实际数据处理中采用附加二阶和三阶傅里叶补偿项的平差模型。

2.2 实际数据验证

试验数据选取两组以不同立体观测方式获取的卫星遥感影像。数据1为北美地区快鸟Basic级同轨立体影像范例数据(图1)，数据2为3景我国河北迁西地区SPOT-5 HRG 1A级异轨影像数据(图3)。两组数据的具体参数见表3，两组数据对应的影像及地面立体覆盖情况如图1—图4所示。

图1 快鸟立体影像缩略图Fig.1 Thumbnail of Quickbird stereo images

图2 快鸟影像立体覆盖及控制点分布Fig.2 Stereo coverage and control point distribution map of Quickbird images

图3 SPOT-5立体影像缩略图Fig.3 Thumbnail of SPOT-5 stereo images

图4 SPOT-5影像立体覆盖及控制点分布Fig.4 Stereo coverage and control point distribution map of SPOT-5 images

表3 卫星遥感影像试验数据参数Tab.3 Parameters of experimental satellite remote sensing image data

两组数据在不同控制点条件下，分别采用一般多项式和傅里叶多项式补偿项的RFM平差定位结果见表4、表5。

表4 快鸟影像平差后定位精度Tab.4 Geopositioning accuracy of Quickbird images obtained by different adjustment methods m

表5 SPOT-5影像平差后定位精度Tab.5 Geopositioning accuracy of SPOT-5 images obtained by different adjustment methods m

从试验结果分析得出：

(1) 采用一阶多项式补偿项(方法1)适用于少量控制点情形，平差后定位精度显著提高。在6个控制点情况下，快鸟影像平差后定位精度从平面9.24 m、高程8.77 m提高到平面1.18 m、高程0.84 m，按地面分辨率0.8 m计，分别相当于1.5、0.8个像元。然而在使用更多控制点情况下，该方法难以进一步提高定位精度，投入全部控制点时平面精度仅为1.4个像元。对于SPOT-5影像，在使用6个控制点情况下定位精度从平面7.78 m、高程9.27 m提高到平面4.38 m、高程3.12 m，按地面分辨率5.5 m计，分别相当于0.8、0.6个像元，使用全部控制点平差后定位精度提升至平面0.7像元、高程0.5像元，提升效果有限。对比两组数据的平差结果，由于SPOT-5影像畸变较小，且测区地表相对平坦，定位精度达到了子像素水平。快鸟卫星由于轨道高度较低，影像分辨率高，内部畸变更为复杂。对快鸟影像用一阶多项式补偿后未达到子像素级定位精度，应系由残余畸变系统误差所致。

(2) 采用二阶多项式补偿项(方法2)适用于充足控制点情形，可进一步消除畸变系统误差，平差后定位精度较高。当所用控制点数少于6时，该方法由于基准不足导致解算不稳定，平差结果无效。在6个控制点情况下，对快鸟影像平差后的高程精度从0.84 m提高至0.76 m，但平面精度从1.18 m下降至1.26 m；SPOT-5影像的平面精度4.38 m提高至3.77 m，但高程精度从3.12 m下降至3.36 m。说明少量控制点情况下，方法2的实际处理效果不稳定，定位精度相比方法1也无优势。而在控制点充足、平差计算稳定性得到保证的情况下，借助二阶多项式更强的畸变拟合能力，方法2较方法1定位精度有明显提高。

(3) 采用傅里叶多项式补偿项(方法3)适用于充足控制点情形，对复杂畸变的拟合补偿性能最优，平差后定位精度最高。在6个控制点情况下，用方法3对快鸟影像平差后的平面和高程定位精度优于方法1和方法2，而对SPOT-5影像平差后的定位精度则较差，说明少量控制点下方法3效果不稳定。而在控制点充足情况下，方法3对两组数据的处理精度均优于方法1和方法2，若采用三阶傅里叶补偿项则优势更加明显。在投入全部控制点情况下，方法3对快鸟影像平差的平面精度比方法1、2可分别提高31%和6%,高程精度可分别提高22%和5%，达到子像素级精度水平；对于SPOT-5影像，尽管常规方法平差结果已达到子像素级精度，但方法3得到的平面精度比方法1、2分别提高10%、3%,高程精度分别提高10%、7%。在3种方法中，方法3具有最高的定位精度，表明傅里叶多项式能够最有效地拟合并消除复杂畸变影响。

3 结 语

针对含复杂畸变的卫星遥感影像高精度几何处理问题，本文基于傅里叶级数的逼近特性，提出了一种附加二元傅里叶多项式补偿项的RFM平差方法。本文方法具有像方平差方案方便实用的特点，通过采用二元傅里叶多项式代替常规一般多项式作为残余系统误差补偿项，可以更加精确地拟合遥感影像中存在的复杂畸变。仿真试验结果表明，本文方法不仅能够消除由于影像内外方位元素误差造成的像方定位系统误差，同时对于不同大小的畸变有很好的拟合补偿能力，平差后平面定位精度接近于像点观测精度的水平。最后对卫星遥感影像的试验结果证实，在充足控制点的条件下，附加三阶傅里叶补偿项的RFM平差定位精度明显优于附加一般多项式补偿项的常规方法，其中对亚米级分辨率快鸟立体影像的平差定位精度可达到子像素级水平。二元傅里叶多项式作为一种畸变拟合性能优越的系统误差补偿模型，理论上具备通用性，不仅适用于高分辨率卫星遥感影像的畸变校正，后续可进一步测试应用于航空和近景影像的畸变校正。