空间碎片激光测距微弱信号实时识别方法
马天明,赵春梅,何正斌,张浩越
中国测绘科学研究院北京房山人卫激光国家野外科学观测研究站,北京 100036
空间碎片长期存在且严重威胁在轨航天器的安全,碰撞事件时有发生[1-3],而卫星激光测距(satellite laser ranging,SLR)技术作为空间碎片轨道测定精度最高的一种技术手段,已被各国用于探测空间碎片,以保障航天安全[4-6]。相比于合作目标,空间碎片属于非合作目标,激光测距技术只能通过接收漫反射回波信号探测空间碎片[7-11],导致空间碎片激光测距回波信号极其微弱,因此,空间碎片激光测距微弱信号识别的研究,对于实现空间碎片激光测距的连续平稳自动跟踪观测、大规模空间碎片快速精密轨道确定与预报具有重要的应用价值和现实意义[12-17],同时可服务于可靠的空间碰撞预警。
目前,国内外围绕激光测距微弱信号实时识别开展了较多的探索和研究。文献[18]提出采用人工屏幕识别方法,该方法是最原始的回波信号识别方法,对微弱信号的适应性好,能有效处理低信噪比的观测数据,但过度依赖于判读人员经验,检测效率和自动化程度低,识别速度慢。文献[19]发展了一种快速回波辨识算法,每次探测到stop事件,计算残差,然后把它与前次存储的1000个残差值进行比较;若在特定带宽内,残差的最小个数大于某个门限值,则将该残差标识为有效信号,该算法对低轨卫星有很高的探测概率,但对于高轨卫星和空间碎片,探测的成功率比较低。文献[20]提出一种基于时间相关性的激光漫反射回波信号快速提取方法,将回波信号提取问题简化为n点搜索问题,并从理论上验证了基于时间相关性提取方法的正确性,试验结果表明该算法漏检率较高,对n点的最优取值需要进一步研究。文献[21]提出了基于回波光子能量积累和抗差估计的实时检测方法,提高了实时有效回波检测效率,降低了错误检测率。利用云南天文台多次实测数据进行了试验,实时检测结果与事后结果对比表明:在有效测量值连续的情况下(时间间距小于2 s),利用该方法基本可以实现准确的实时检测;当有效测量值稀疏时,错误检测率显著增加。文献[22—23]均提出采用泊松统计滤波算法提取回波信号,认为噪声点服从泊松分布,而光子回波残差在短时间间隔内落在未知斜率的一段直线上,用倾斜的矩形窗在短时间间隔内对数据进行扫描,辨识出局部信号统计特征,提取出不满足泊松分布的窗口范围,即判定为有效数据,但该方法检测结果受泊松统计滤波影响较大,对数据处理的自适应性不强。
为解决激光测距探测空间碎片噪声点多,回波信号微弱,无法快速准确识别的问题,本文提出一种基于时间相关性的空间碎片激光测距微弱信号实时识别算法,并利用空间碎片实测观测数据对算法进行了验证,实现了空间碎片激光测距微弱信号的实时识别,提高了空间碎片的探测成功率。
1 二次滤波算法原理及其不足
目前,大多数激光观测站在信号实时识别方面均采用二次滤波识别算法,该算法由Graz观测站率先提出并实际应用。在合作目标尤其是中低轨卫星的激光测距中,目标的预报轨道精度较高,回波信号O-C(observations-calculates)残差变化不大,基本为一条直线,如图1所示,其中O-C残差指的是将空间目标实际观测过程中探测到的回波时间与空间目标的预报回波时间作差得到时间残差,也称为观测残差。图2为图1的局部放大,可以看出回波信号的O-C残差值都在一个固定的很小的范围内。二次滤波算法就是根据上述回波信号的特点,将当前回波的O-C残差值与前面相邻的若干O-C残差值进行比较,如果差值在规定的范围内,则认为当前回波点为有效回波信号点[24],具体数学表达如式(1)所示

图1 Ajisai卫星O-C残差Fig.1 O-C residuals of Ajisai satellite
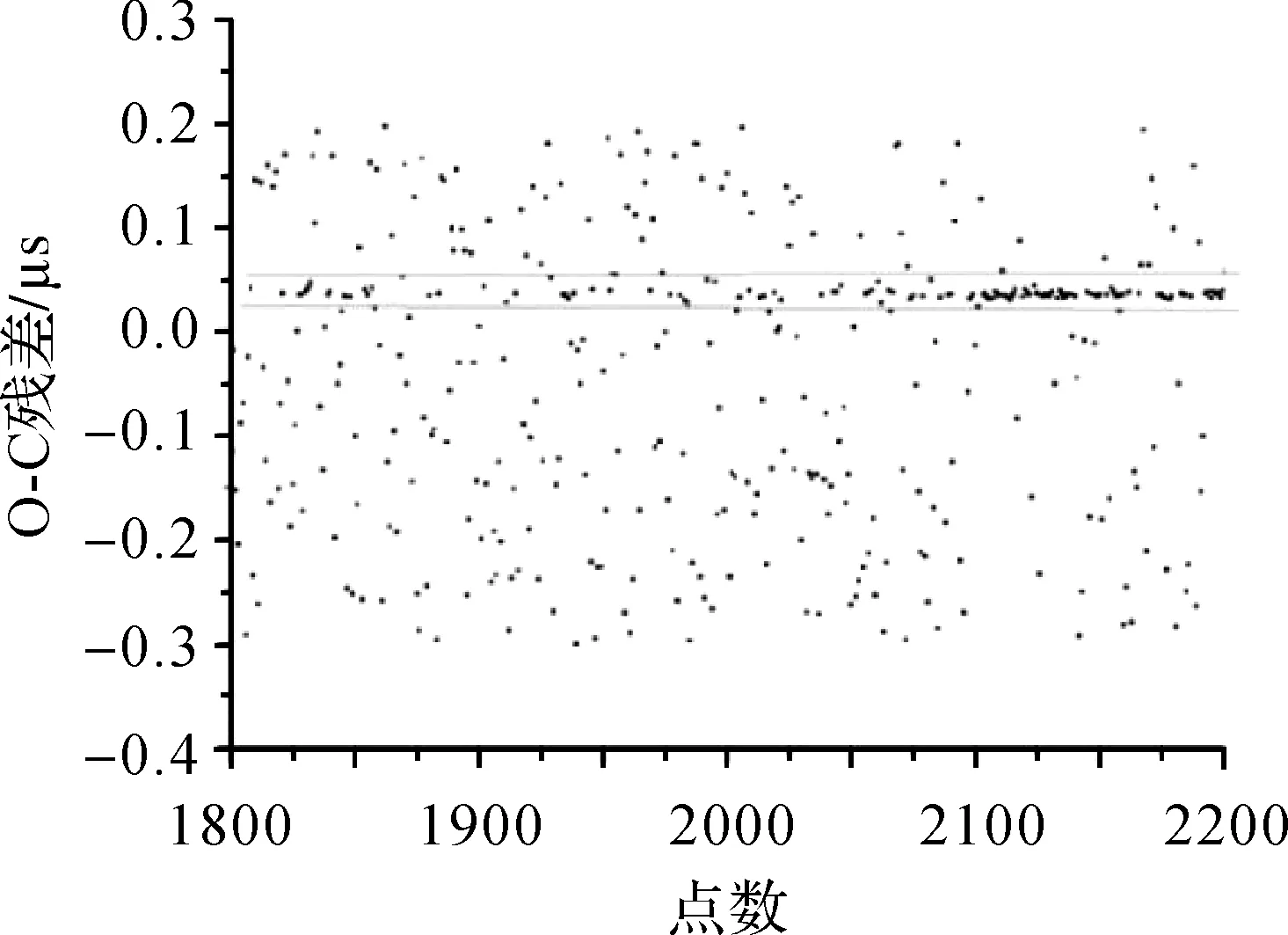
图2 Ajisai卫星O-C残差的局部放大Fig.2 Local amplification of O-C residuals of Ajisai satellite
|ΔR-ΔRn|<δ
(1)
式中,ΔR为当前获得的测站到卫星的O-C值;ΔRn为之前第n次获得的测站到卫星的O-C值;δ是比较阈值,其取值取决于系统的观测误差及观测目标的预报精度。
1.1 一次滤波算法
一次滤波识别过程中,识别参数的设置与激光测距系统参数息息相关,本文以北京房山激光测距系统为例进行参数设置。
式(1)中,n取值为1000,δ取值为1000 ps,在滤波过程中,将当前的O-C观测残差与之前的1000次O-C观测残差进行比较,如果差值结果小于1000 ps,那么将计数器累加1次,在1000次比较中,如果大于等于m(这里m取3)次差值结果小于1000 ps,则认为当前回波信号为有效回波信号。为识别更多的有效回波信号,滤除更多的噪声点,可以通过提高m值和n值进行滤波,但是提高m值对于回波率较低的观测目标难以识别出有效回波,而提高n值会增加比较的次数,增加计算机的计算量和计算时间[25],达不到实时识别的效果,因此,需根据系统参数合理确定m值和n值。因此,为了提高滤波的识别效果,在一次滤波的基础上进行二次滤波识别。
1.2 二次滤波算法
二次滤波即对一次滤波识别出的所有观测数据再进行一次滤波,二次滤波过程中,原理同一次滤波原理相同,但是滤波参数略有差异。在二次滤波中,n取最大值为300,δ值取为500 ps,m值取为3,将当前O-C值与前面的300个O-C值进行比较,如果差值小于500 ps,则计数器累加1,在300次的比较中,如果大于等于3次差值结果小于500 ps,则认为当前回波信号为有效回波信号。
二次滤波的优点在于仅仅增加了300次的比较时间,但是较一次滤波效果要更加明显,在回波信噪比较高的观测目标信号识别过程中效果较好。二次滤波方法具体流程如图3所示。
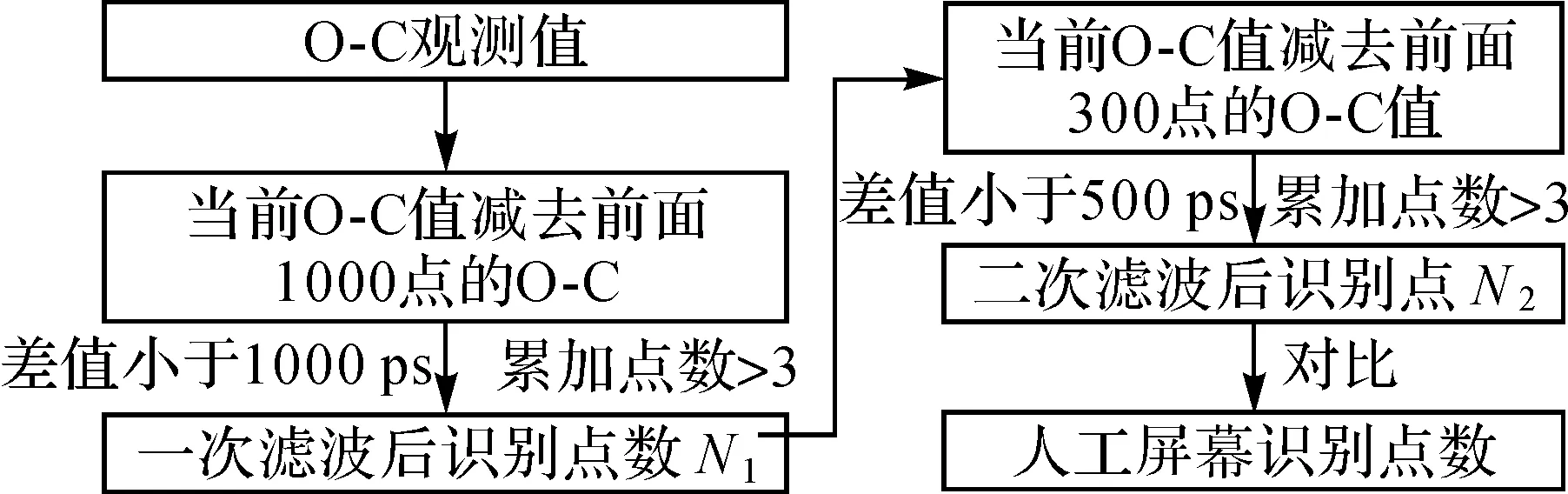
图3 二次滤波算法Fig.3 Secondary filtering algorithm
1.3 二次滤波算法的不足
在高信噪比的有效回波识别中,二次滤波算法能够较好地发挥作用,但是在空间碎片探测过程中,由于激光测距只能接收漫反射回波信号,导致回波信号十分微弱,因此,二次滤波识别算法在探测空间碎片过程中识别正确率不足1%。图4为通过二次滤波识别算法识别后的空间碎片22076识别结果。由图4可以看出,二次滤波识别算法在识别有效回波信号的同时,也识别了很多噪声点。在空间碎片激光测距过程中,研究微弱信号的实时识别,对提高空间碎片的探测成功率具有重要意义。图5为二次滤波识别结果。
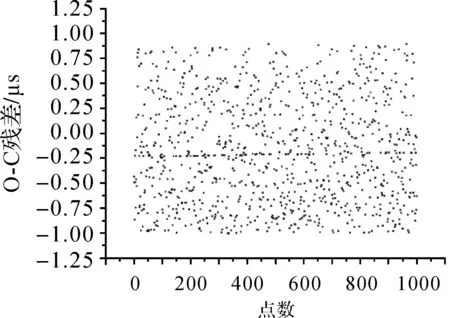
图4 空间碎片22076观测数据O-C残差Fig.4 O-C residuals of observation data for space debris No. 22076
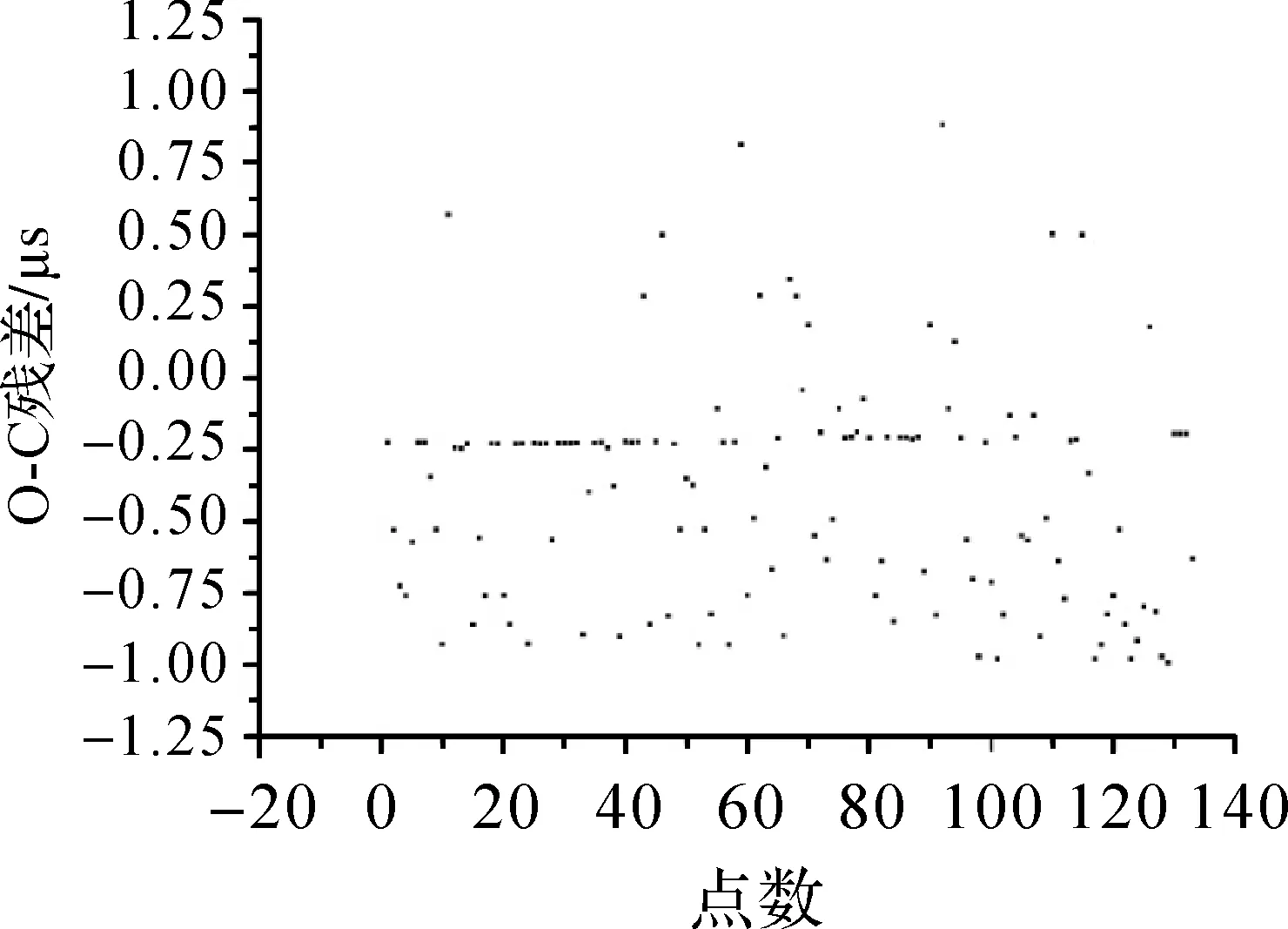
图5 二次滤波识别结果Fig.5 Recognition result of secondary filter observation data
2 微弱信号实时识别算法
针对二次滤波算法在探测空间碎片过程中实时识别有效回波信号的不足,根据空间碎片回波信号的特点,本文提出在一次滤波的基础上,利用线性拟合的方式进行微弱信号实时识别。
与二次滤波算法相同,先进行一次滤波识别,设一次滤波后得到的识别点数为N1;在接下来的识别中,将n值取为30,考虑到回波信号在很短的时间内呈现直线分布,对这30个O-C残差值进行线性拟合,但在拟合之前,先根据这30个点的标准差去掉其中误差较大的点;然后求解剩余点的O-C残差值的拟合残差σ;最后将当前O-C残差值代入拟合直线求解拟合残差σ′,如果当前O-C值拟合残差满足σ′<2.5σ,则认为当前回波信号为有效回波信号。具体过程如下。
(1) 筛选一次滤波后前n个点中符合要求的点,公式如式(2)—式(4)所示
(2)
(3)
(4)
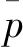
(2) 利用n′个数据点进行线性拟合,如式(5)所示
(5)
式中,a、b分别为线性拟合的相关系数;m为n′个数据点的序号,根据式(5)建立的线性拟合公式,解算n′个数据点到该线性拟合的拟合残差,公式如式(6)所示
σ=sqrt
(6)
(3) 将当前点序号代入建立好的线性拟合公式,求解当前点的O-C残差计算值,根据当前点的O-C计算值与当前点的O-C观测值求解当前点的O-C观测值与线性拟合之间的拟合残差,当该偏差小于2.5倍σ时,则当前点被认为是有效信号点。
微弱信号实时识别方法整体流程如图6所示。

图6 微弱信号实时识别方法Fig.6 Real-time identification method for weak signal
基于高重复频率激光测距系统探测空间碎片,需要保存的数据量非常庞大,通常有几十万至几百万个数据点,因此,本文提出的微弱信号实时识别算法在提高识别精度的同时,还需要考虑识别效率的问题,以减少CPU的运行时间。在对空间碎片进行观测的过程中,如果所有观测数据点均显示在屏幕上,会造成程序运行缓慢,数据识别效率低下。因此,本文提出的微弱信号实时识别算法因为识别精度接近人工屏幕识别精度,在空间碎片观测过程中,屏幕只显示识别的数据点,对其余数据点进行隐藏。如果识别点数在1000以下,则全部显示;如果超过1000点,则求出识别点数相对1000的倍数。因此,根据这个倍数均匀的选择需要显示的数据点。如识别点数为6000,则每识别6个数据点选择1个数据点显示在屏幕端,则保证显示点数在1000左右。根据上述算法的设置,假如共观测20 000数据点,都显示在屏幕上需要20 s完成,而按照本文算法的显示设置,1 s即可完成,大大减少了CPU的运行时间,从而提高了空间碎片的观测效率和观测成功率。需要说明的是,虽然屏幕上未显示所有的数据点,但隐藏的数据点同样参与最后的数据预处理,对处理结果没有影响。
3 试验数据分析
本文提出的微弱信号实时识别算法主要针对距离在1000 km,角速度在0.1 rad/s以内、尺寸为米级的火箭体具有较好效果。为了验证本文提出的微弱信号实时识别算法的有效性,利用北京房山SLR站观测到的空间碎片观测数据进行了试验验证,本文试验研究的数据是北京房山人卫站在2019年年底至2020年年初观测的4颗空间碎片的实测观测数据。碎片轨道高度均在1000 km左右,属于近地轨道空间碎片,升交点赤经广泛分布在0°~360°,绕行时间均在100 min左右,角速度为0.6 rad/s,其中碎片27386、31114和28480的轨道倾角均为98°左右,碎片22076的轨道倾角为66°左右。空间碎片的编号、观测时间、尺寸、升交点赤经和轨道偏心率等参数见表1。

表1 北京房山SLR站空间碎片激光测距试验结果Tab.1 Experimental results of space debris laser ranging at Beijing Fangshan SLR station
分别利用二次滤波算法和本文提出的微弱信号实时识别算法对观测数据的O-C残差值进行识别,识别结果如图7—图10所示。
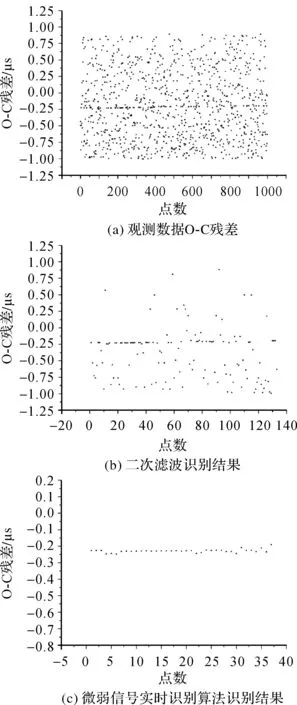
图7 空间碎片22076观测及识别结果Fig.7 The observation and identification results of space debris No. 22076

图8 空间碎片27386观测及识别结果Fig.8 The observation and identification results of space debris No. 27386
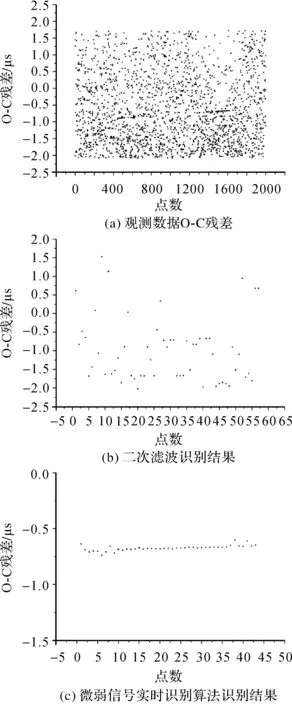
图9 空间碎片31114观测及识别结果Fig.9 The observation and identification results of space debris No. 31114

图10 空间碎片28480观测及识别结果Fig.10 The observation and identification results of space debris No. 28480
由图6—图9可以看出,面对空间碎片的微弱信号源,本文提出的微弱信号实时识别算法依然能够有效地识别出回波信号,进一步验证了模型的有效性。为了进一步比较二次滤波模型和本文提出的微弱信号实时识别算法的识别精度,对两种模型识别点数和误检/漏检率进行统计,结果见表2。
表2中的信噪比、误检率和漏检率的计算公式如式(7)—式(9)所示

(7)

(8)

(9)
由表2可以看出,二次滤波识别点数与人工屏幕识别点数相差非常大,误检率和漏检率较本文提出的微弱信号实时识别算法高出一个量级,平均误检率达到5.72%,漏检率达到0.77%,而本文提出的微弱信号实时识别模型识别点数与人工屏幕识别点数非常接近,虽然也存在误检和漏检的情况,但平均误检率和漏检率分别只有0.12%和0.34%,证明利用本文提出的微弱信号实时识别算法能够有效识别空间碎片的微弱回波信号。

表2 空间碎片微弱信号识别模型精度对比Tab.2 Accuracy comparison of weak signal recognition models for space debris
本文提出的微弱信号实时识别算法在要求具有较高识别精度的同时,也要求算法具有较高的实效性,因此,对二次滤波识别模型和本文提出的微弱信号实时识别算法的运行时间进行了统计,文中所用到的二次滤波识别算法和微弱信号实时识别算法均是在VS2010平台采用C++编程语言实现的,试验所用的计算机配置为i5处理器的戴尔电脑,CPU为3.20 GHz,RAM为16.0 GB,对每个算法进行了1000次计算,每种算法的平均计算时间见表3。

表3 两种算法的平均计算时间Tab.3 Average calculating time of two algorithms
由表3可知,两种算法的平均计算时间相当,证明本文提出的微弱信号实时识别算法在保证识别精度的同时,也具有较好的实效性。为了进一步验证模型的有效性,利用识别数据形成激光测距标准点数据,并根据标准点数据计算每圈(这里圈指的是卫星过境次数,过境一次则称为1圈)数据的时间偏差和距离偏差,计算原理如下。
根据观测目标的预报值和观测数据建立误差观测方程
Δρ=ρ0-ρc
(10)
式中,ρ0为卫星到观测站的实际观测值;ρc为卫星到观测站的预报值;Δρ为观测残差。近似认为观测残差Δρ由时间偏差TB和距离偏差RB组成,则有
Δρ=RB+TB·ρ′
(11)
式中,ρ′为卫星的视向速度。根据式(11)采用最小二乘即可解算每圈观测数据的时间偏差和距离偏差。
计算结果如图11所示,4颗空间碎片(共6圈)数据中,时间偏差最大值为628.05 ms,最小值为48.76 ms;距离偏差最大值为515.2 m,最小值为256 m,上述统计结果表明,北京房山卫星激光观测站DLR系统探测精度满足空间碎片的探测要求,进一步验证了数据识别模型的有效性。

图11 观测数据时间偏差与距离偏差Fig.11 Time deviation and distance deviation of observation data
4 结 论
本文针对二次滤波识别算法在微弱信号识别中效果较差的问题,提出在一次滤波的基础上,进行线性拟合,实现微弱信号的实时识别。并利用北京房山卫星激光观测站的空间碎片观测数据对本文所提出的模型进行了验证,结果表明,本文提出的微弱信号实时识别算法能够较好地实现微弱信号的实时识别,误检率和漏检率分别由原来的5.72%和0.77%降低到0.12%和0.34%,且实时性与二次滤波算法相当,为北京房山激光观测站提高空间碎片的探测成功率提供了有力保障。

