顾及双程声径的常梯度声线跟踪水下定位算法

闫凤池，王振杰，赵 爽，聂志喜，孙 振，李伟嘉

中国石油大学(华东)，山东 青岛 266580

海洋是人类资源环境可持续发展的希望[1]。海洋导航定位技术是海洋开发和海洋高技术应用的基本前提，是进行海洋活动的重要基础[2]。由于电磁波在海水中衰减速度过快，无法满足水下定位的需要[3]，而声波因其良好的传播特性，可以进行远距离、大深度的传播，得到广泛的研究和应用，成为水下定位的主要观测手段[4]。

海洋中，声速受海水温度、盐度、密度、海流等各种复杂海洋环境的影响，给高精度水下声学定位带来了极大挑战[5]。水下声学定位中最为显著的误差是声线弯曲误差和声速误差，为了消除或减弱声线弯曲误差的影响，需要进行声速改正[6]。目前，常用的水下定位声速改正方法有加权平均声速法、等效声速法、声线跟踪法等[7]。其中，加权平均声速法最为简单，但定位精度受限[8]；等效声速法可以有效地提高定位的精度，但无法完全消除声线折射效应的影响[9]；声线跟踪法对声信号进行了声线弯曲改正，计算精度最高[10]。

为削弱声速误差等系统误差对定位的影响，可以采用差分定位的方法，包括空间差分和历元间差分两种模式。空间差分类似于GNSS差分定位技术[11]，削弱观测值中的共性误差，但也抵消了非差观测值中的垂向信息，降低了竖直方向的定位精度。文献[12]提出历元间差分方法，通过对相邻观测历元之间的差分，削弱与时间相关联的系统误差影响。文献[13]将抗差估计与差分定位结合，提出了基于抗差估计的历元间单差和双差定位模式，不仅削弱时间关联误差的影响，同时有效控制了异常误差的影响。

文献[14]顾及声速相关系统误差的相似性，提出采用差分组合观测值方法。假设局部范围内声速稳定，声速对测距影响近似相同，借助距离差解算海底应答器坐标，虽然削弱声信号传播时间上的系统误差影响，但该方法垂直定位结果不稳定。文献[15]提出利用最小二乘反演法确定海底应答器阵列位置，通过不同应答器之间的基线长和相对深度差对应答器坐标进行约束。但距离计算采用平均声速法，且模拟试验中测量船始终位于应答器阵列中心位置上方海面，因此有一定局限性。以上方法虽然在一定程度上提高了水下定位的精度，但由于未能考虑到声信号往返的实际原理，因此定位精度有限。

考虑到声速误差不仅与复杂的海洋环境有关，也受到观测仪器自身的限制[16]。当利用观测区域的声速剖面进行声线跟踪时，理论上可以完全消除声线弯曲影响[17]，但考虑到水下声信号传播的实际情况及船载换能器在声信号传播过程中的位移，需要构建更加合理的定位模型[18]。

目前，水下声学定位方法通常采用基于声信号的单向传播路径(单程声径)，忽略了测量船持续走航引起的换能器在声信号传播过程中的位置移动，进而会降低应答器定位精度[19]。针对上述问题，本文结合水下声学定位中声信号实际传播过程，构建了顾及声信号双向传播路径(双程声径)的定位模型，发展了基于双程声径的分层常梯度声线跟踪定位算法。

1 单程声径水下定位方法

单程声径水下定位的原理是将船载换能器测量的声信号往返时间取二分之一作为其单程传播时间，结合已知声速剖面，获得船载换能器与海底应答器之间的斜距，然后利用多个斜距建立误差方程组，通过最小二乘求解非线性方程组获得海底应答器位置[20]。单程声径水下定位原理如图1所示。

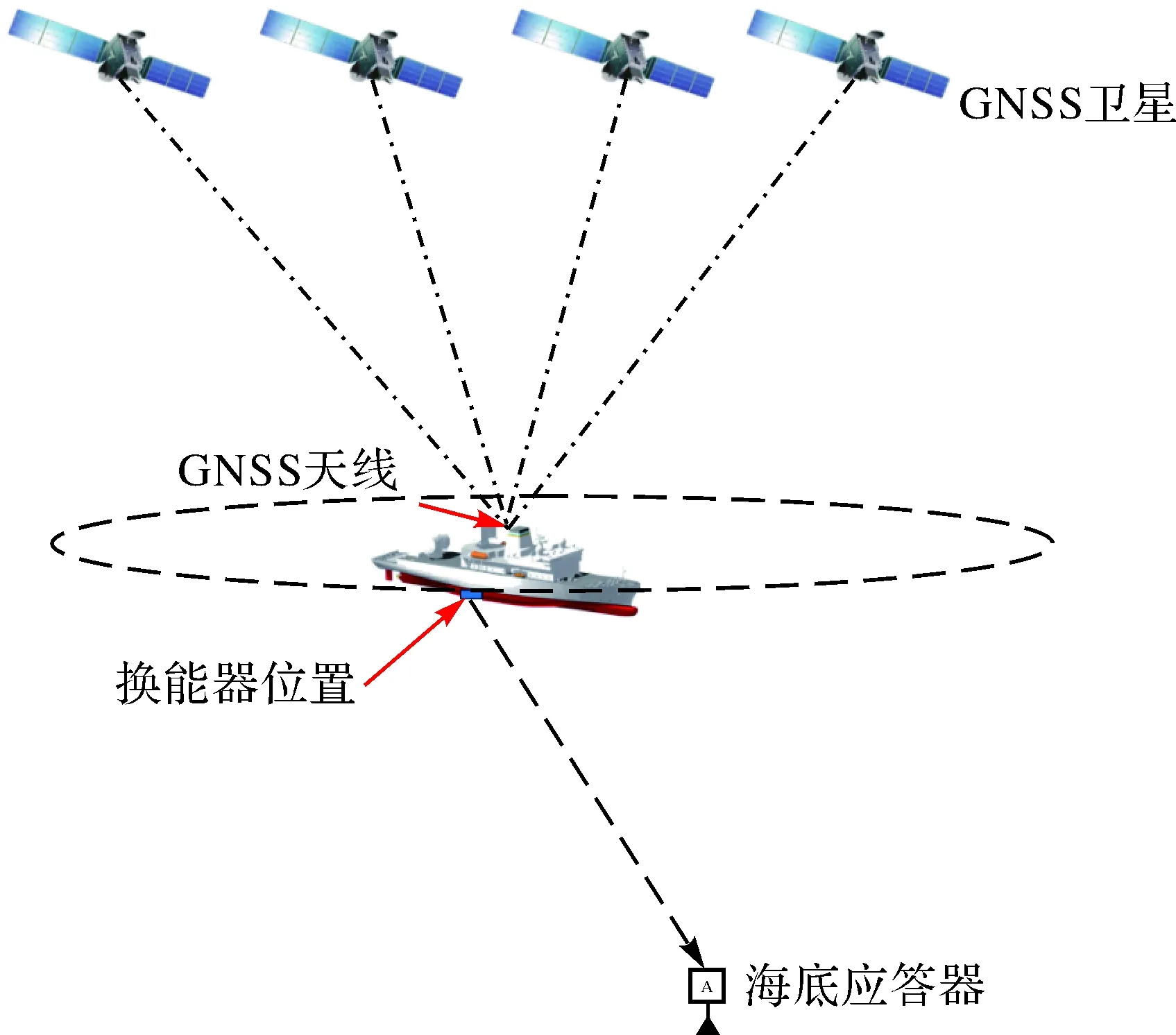
图1 单程声径水下定位原理Fig.1 Principle of high precision underwater positioning with single-trip acoustic path

1.1 单程声径水下定位模型

在单程声径水下定位过程中，假设海底应答器坐标为Xo(x0,y0,z0)，通过船载GNSS接收机获取测量船的位置信息[21]，如图1所示。结合测量船的姿态传感器测得的姿态信息，计算出船载换能器各历元的坐标Xi(xi,yi,zi)，观测历元i=1,2,…,n。船载换能器测量的声信号往返时间间隔2ti，则单向传播时间为ti。在已知声速剖面的情况下，通过单程声径声线跟踪算法计算船载换能器到海底应答器之间的几何距离ρi，具体计算方法见1.2。

单程声径水下定位模型为[22]

ρi=f(Xi,Xo)+δρdi+εi

(1)

式中，f(Xi,Xo)是船载换能器到海底应答器的真实几何距离；δρdi是与声速和测时有关的系统误差；εi是随机误差。

船载换能器到海底应答器的真实几何距离f(Xi,Xo)表示为

(2)

将式(1)线性化，可得

(3)

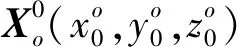
在忽略各类系统误差的情况下，单程声径水下定位观测方程为

L=AdX+Δ

(4)

式中，L是n维的观测向量；A是n×3的系数矩阵；dX是海底应答器坐标改正数；Δ是由多个历元的εi+biεXi组成的矩阵。

观测向量

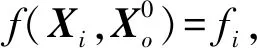
通过最小二乘求解海底应答器坐标改正数为

dX=(ATPA)-1ATPL

(5)

式中，P为观测值的权矩阵，可基于声线入射角确定或根据验后残差进行确定[12]。

观测值改正数

V=AdX-L

(6)

分别计算单位权中误差和协方差阵

(7)

式中，r为多余观测数；n为总观测数；t为必要观测数，一般为3；QXX为平差参数的协因数阵。

1.2 单程声径声线跟踪算法

声线跟踪的理论基础是声速分层假设，即任何复杂的声速剖面结构，都可以近似为由多层具有简单结构的声速层组成。此假设用每个独立层内的声速折线分布来代替整个声速剖面的连续变化。目前，常用的声速分层形式有常声速分层和常声速梯度分层两种，其中，常声速分层认为每层内声速不变，声线沿直线传播；常声速梯度分层认为层内声速线性变化，声线沿曲线传播。本文采用的是常梯度声线跟踪法。假设将声信号经过的水柱分为N个等梯度层，层内声速的变化是常梯度的，即认为层内声速线性变化[24]。通过逐层跟踪的方法计算声信号的水平位移、竖直位移和传播时间，如图2所示。

图2 单程声径声线跟踪算法Fig.2 Acoustic ray-tracing algorithm of single-trip acoustic path

在水深zi对应的i层，用ci表示声信号的传播速度。第i层内的声速梯度gi可以用式(8)表示为[25]

(8)

式中，Δzi为第i层的水层厚度，ci+1为第i+1层声速。

在第i层内，声线曲率处处相等，声线在层内的轨迹为一段圆弧。该圆弧的曲率半径为[26]

(9)

式中，p是Snell常数。

由Snell定律和常梯度声速假设[27]，声信号在第i层内的水平距离Δyi，竖直距离Δzi和时间Δti为

(10)

式中，θi和θi+1分别为声信号的入射角和出射角。

对完整层进行声线跟踪后，需要依据声信号剩余传播时间进行剩余层的计算。假设剩余时间为tr，则

(11)

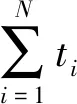
声信号在剩余层的水平位移和竖直位移为

(12)

声信号的总水平位移和总竖直位移为

(13)

改正后几何距离为

(14)

将ρi代入式(1)，构建单程声径声线跟踪的观测方程，通过式(5)求解海底应答器坐标改正数，通过迭代计算完成单程声径水下定位[28]。

该方法得到的单程声径几何距离与真实声线基本一致，有效地提高了传统的水下声学定位方法的定位精度，这也是目前水下定位中最常用的方法之一。但单程声径模型存在局限性，即忽略了换能器在声信号往返过程的位置变化，直接利用换能器声信号发射或接收时刻的坐标进行解算，获得海底应答器的坐标，从而降低了海底应答器位置解算精度。

2 双程声径水下高精度定位

测量船在海面持续走航过程中，船载换能器在声信号发射和接收时的位置会发生变化，故声信号往、返的路径存在差异。若忽略换能器的位置变化，只考虑声线单向传播过程，将会在海底应答器定位解算时引入系统性偏差，降低水下定位的精度。针对单程声径水下定位方法中存在的问题，为削弱换能器位置变化对水下定位的影响，有必要研究更符合水下声学定位实际的模型和解算方法。如图3所示，本文利用船载换能器声信号发射和接收时刻的位置计算声信号传播的双程声径几何距离，构建双程声径水下高精度定位模型，通过解算，实现海底应答器的高精度定位。

图3 双程声径水下高精度定位原理Fig.3 Principle of high precision underwater acoustic positioning with round-trip acoustic path

2.1 双程声径水下高精度定位模型

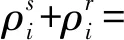
(15)

将式(15)线性化后，得

bidX+δρdi+εi+niεXi

(16)

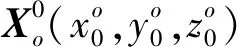
在忽略各类系统误差的情况下，双程声径水下高精度定位观测方程为

L=BdX+Δ

(17)

式中，L是n维的观测向量；B表示n×3的系数矩阵；dX是海底应答器三维未知坐标改正数；Δ是随机误差向量。

将观测方程展开可得

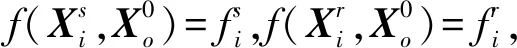
通过最小二乘求解海底应答器坐标改正数

dX=(BTPB)-1BTPL

(18)

观测值改正数

V=BdX-L

(19)

式中，P为观测值的权矩阵，可基于声线入射角确定或根据验后残差进行确定。

分别计算单位权中误差和协方差阵

(20)

式中，r为多余观测数；n为总观测数；t为必要观测数，一般为3；QXX为平差参数的协因数阵。

2.2 双程声径声线跟踪算法

顾及声信号的实际往返传播路径，基于分层常梯度声线跟踪算法进行双程声径声线跟踪，如图4所示，结合声信号往返时间，计算声信号往返的几何距离，实现海底应答器位置的准确解算。

图4 双程声径声线跟踪算法Fig.4 Acoustic ray-tracing algorithm of round-trip acoustic path

如图4所示，在进行双程声径声线跟踪前，需要已知声速剖面，根据声速剖面计算各层的声速梯度gi，由于声信号往返时间较短，故认为声速剖面结构未发生变化，已知声信号自上向下的传播时间和自下向上传播的传播时间之和等于总传播时间，采用相同的分层结果对往返的声线进行跟踪，具体过程可以分为以下3步。

第1步：声信号自上向下传播。设在声信号发射时刻的声速剖面的第i层内，声线曲率处处相等，声线在层内的轨迹为一段圆弧，该圆弧的曲率半径为Rsi。

由Snell定律和常梯度声速假设，声信号在第i层内传播的水平距离，竖直距离和时间为

(21)

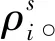
第2步：声信号自下向上传播。设在声信号接收时刻的声速剖面的第i层内，声线曲率处处相等，声线在层内的轨迹为一段圆弧，该圆弧的曲率半径为Rri，由于声线自下向上进行追踪，故每层的声速梯度为-gi。

由Snell定律和常声速梯度假设，声信号在第i层内传播的水平距离，竖直距离和时间为

(22)

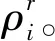
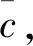
L=B′dX+Δ′

(23)

通过最小二乘求解海底应答器坐标改正数

dX=(B′TPB′)-1B′TPL′

(24)

得改正后的海底应答器坐标

Xnew=Xo+dX

(25)

将改正后的海底应答器坐标Xnew代入第1步，再次进行双程声径声线跟踪，并进行收敛判断，直至满足收敛阈值要求，则双程声线跟踪完成。利用双程声径声线跟踪建立传播时间与往返距离的关系，利用双程声线跟踪获得的声信号往返几何距离构建双程声径观测方程，通过式(24)解算海底应答器的坐标改正数，完成双程声径水下高精度定位。

与单程声径声线跟踪相比，双程声径声线跟踪顾及了测量船在走航中换能器的位置变化，通过将声线跟踪过程分解为自上向下的去程和自下向上的返程，并结合声学观测时间，实现声信号往返双程声径的准确跟踪，该算法相比单程声径声线跟踪定位更符合水下声信号传播实际。

3 试验与分析

2019年7月，笔者所在团队在我国南海海域开展了海洋大地测量基准与海洋导航新技术深海综合试验，试验区域平均水深约3000 m。测量船搭载GNSS接收机、高精度姿态传感器、声速剖面仪和海面长基线定位系统等设备。本文中的往返时间是已知观测值，通过测量船的相关仪器设备观测得到。为了减小声速剖面时空差异对定位的影响，试验采用走航观测前后的声速剖面平均值进行定位解算。分别采用圆走航观测和交叉十字观测。

首先，测量船以圆形航迹对海底基准点进行了连续观测，圆走航半径约为1.5倍水深，测量船航速设定约为1.00 m/s，即1.95 kn，声信号往返过程中测量船平均水平位移为7.85 m，观测历元共1080个，走航航迹及应答器位置示意图如图5所示。在测区内进行声速测量，绘制声速剖面如图6所示。经过粗差剔除、坐标系统转换及姿态改正等数据预处理后，分别采用单程声径声线跟踪和双程声径声线跟踪方法进行解算，观测值权矩阵基于声线入射角确定，圆走航观测下个各历元的声线入射角如图7所示，海底应答器解算坐标及其精度统计见表1，精度指标对应于协方差阵Dxx的对角线上的元素。

图5 圆走航观测航迹与海底应答器位置 Fig.5 Circularsurveying track and the seafloor transponder

图6 声速剖面 图7 圆走航声线入射角Fig.6 Sound velocityFig.7 Incidence beam angles profile of circular surveying

表1 圆走航观测下海底应答器定位结果统计Tab.1 Statistical table of positioning results for seafloor transponder by the circular surveying track m

由表1可以看出，单程声径声线跟踪与双程声径声线跟踪水平方向互差为0.161 m，竖直方向互差0.034 m，即在圆走航观测模式下，换能器位置变化对海底应答器定位的影响主要体现在水平方向。比较单程声径声线跟踪和双程声径声线跟踪的定位内符合精度，可以发现双程声径无论在水平方向还是竖直方向的内符合精度均明显优于单程声径。

圆走航观测模式下单程声径声线跟踪和双程声径声线跟踪的残差值，如图8所示。可以看出两种方法的残差分布较为接近，波动范围为-1.500 m～1.500 m，均呈现出正态随机分布的特点。分析圆走航观测残差的统计特征，包括平均值(mean)、最大值(max)、标准差(std)、均方根(RMS)见表2。

图8 圆走航观测残差分布直方图Fig.8 Histogram of residual distribution in circular surveying track

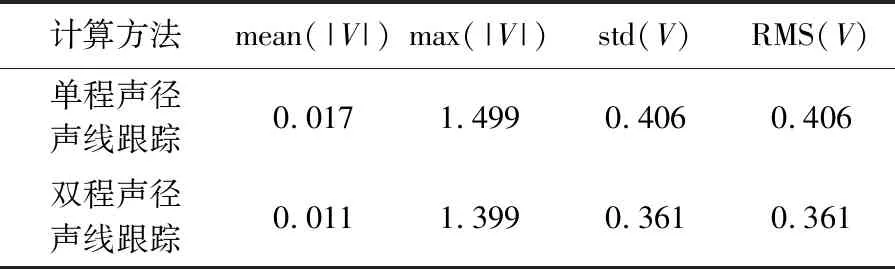
表2 圆走航观测残差统计结果Tab.2 The residual statistical results of circular surveying track m

由表2可以看出，双程声径声线跟踪在平均值、最大值、标准差、均方根上均略优于单程声径声线跟踪。由图7可以看出，圆走航观测模式下，声线入射角波动较小，单程声径和双程声径的变化基本可以忽略。考虑到圆走航观测结构对称，在平差过程中部分系统误差被消除，故双程声径声线跟踪的优势体现不明显，需要进一步考虑交叉十字观测结构对定位的影响。

测量船沿交叉十字航迹对多个海底应答器进行连续、同步观测，测量船航迹和海底应答器位置如图9所示，测量船的航速设定约为1.83 m/s，即3.56 kn，声信号往返过程中测量船平均水平位移为11.63 m。5个应答器对应观测历元分别为1795、1827、1821、1838和1735个。以5号应答器为例，根据其概略坐标计算不同观测历元下该应答器对应的声线入射角变化，如图10所示。不同观测历元下中心点对应的声线入射角最小0.65°，最大45.29°，平均声线入射角29.26°。可以发现，当测量船沿交叉十字航迹进行测量时，声线入射角波动较大，观测值权矩阵基于声线入射角确定。图11为十字交叉观测5号应答残差分布。

图9 交叉十字观测航迹与海底应答器Fig.9 Coss tracking lines and the seafloor transponders

图10 各历元下5号应答器对应的声线入射角Fig.10 Incidence beam angles of No.5 transponder under each epoch

图11 十字交叉观测5号应答器残差分布直方图Fig.11 Histogram of residual distribution with No.5 transponder in cross tracking lines

经过粗差剔除、坐标系统转换及姿态改正等数据预处理后，分别采用单程声径声线跟踪和双程声径声线跟踪方法进行解算，各应答器解算坐标及其精度统计见表3、表4。

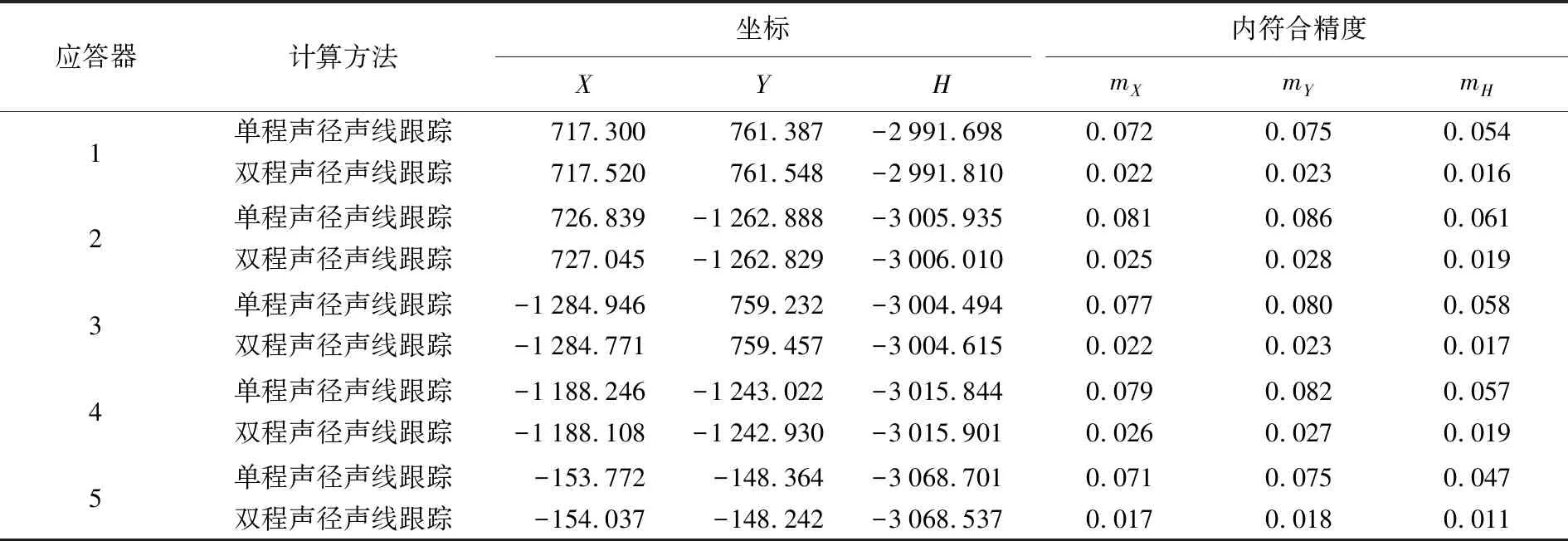
表3 交叉十字观测定位解算结果统计Tab.3 Statistical table of cross tracks location m

对表3和表4试验结果分析：

表4 十字交叉观测5号应答器残差统计结果Tab.4 The residual statistical results of No.5 transponder in cross tracking lines m

(1) 从海底应答器坐标解算结果分析，单程声径声线跟踪与双程声径声线跟踪水平方向互差最大为0.285 m，最小为0.166 m；竖直方向互差最大为0.145 m，最小为0.057 m。不难发现在交叉十字观测模式下，换能器位置变化对海底应答器定位的影响依旧主要体现在水平方向，且较圆走航两种方法互差进一步加大。对比5号应答器在圆走航和十字交叉观测下的互差，单程声径声线跟踪在两种不同观测航迹下水平方向互差为0.372 m，竖直方向互差为0.533 m；双程声径声线跟踪在两种不同观测航迹下水平方向互差为0.306 m，竖直方向互差为0.335 m。可以看出双程声径声线跟踪在不同观测航迹下的互差明显小于单程声径声线跟踪，即该方法具有较高的定位精度。

(2) 从定位精度分析，各海底应答器双程声径声线跟踪的内符合精度均优于单程声径声线跟踪，且非中心位置的4个海底应答器坐标的内符合精度基本一致。对于中心位置的应答器，双程声径内符合精度较单程声径提高了近一半。结果表明，双程声线跟踪可以有效提高水下定位精度，尤其在非对称观测条件下，效果更加明显。对比不同观测航迹的内符合精度，可以发现，圆走航模式下的内符合精度优于十字交叉走航的内符合精度，证明了观测航迹的结构对于定位的精度有较为明显的影响。

(3) 为进一步评价定位结果的可靠性，以5号海底应答器为例，采用不同观测方式下5号海底应答器的计算结果均值为参考。由于海底应答器坐标的真值无法获取，通常是采用多次观测的平均值作为最或然值，即不同航迹下单程、双程声线跟踪坐标解的平均值。因为不同观测方案是在不同日期进行的，互为独立观测，可以进行相互检核。分析得到单程声径声线跟踪与参考值水平方向差为0.281 m，竖直方向差为0.299 m，双程声径声线跟踪与参考值水平方向差为0.141 m，竖直方向差为0.135 m。从残差平均值来看，单程声径为0.219 m，双程声径为0.154 m；从残差均方根来看，单程声径为2.561 m，双程声径为1.038 m。可以看出，当采用双程声径声线跟踪时，残差均方根等明显变小，较单程声径声线跟踪有更好的定位效果。如果进一步优化函数模型，改化算法，有望获得更优的坐标精度，优化处理模型和改化算法涉及面较多，将另文讨论。

4 结 论

在水下高精度定位中，声速误差是影响声学定位精度的重要原因，采用声线跟踪的方法可以有效地削弱声线折射效应的影响，但基于单程声径水下定位模型，没有考虑声信号往返过程中船载换能器的位置变化，导致单程声径声线跟踪算法存在建模误差，降低了水下声学定位精度。本文算法，考虑了水下定位过程中声信号传播的实际情况，利用测量船持续走航引起的换能器位置变化信息，通过建立双程声径水下定位模型，实现水下声学高精度定位，得到了以下结论：

(1) 在圆走航观测情况下，测量船沿圆航迹行进，换能器与应答器之间的往返声径变化较小，双程声径声线跟踪对海底应答器定位精度有一定的提升，主要体现在水平方向。

(2) 在交叉十字观测情况下，测量船沿直线航迹行进，换能器与应答器之间的往返声径不断变化，需要考虑换能器位置变化对海底应答器定位的影响。通过对双程声径和单程声径两种解算方法的海底应答器坐标解残差的对比，可以发现双程声径声线跟踪能有效提高海底应答器的定位精度，尤其在非对称观测条件下，改善效果更加明显。

本文在解算过程中忽略了系统误差的影响，下一步将针对水下声学定位的系统误差，考虑采用半参数法等最优参数估计方法，研究系统误差处理策略，完善双程声径声线跟踪算法，以期实现更高精度的水下声学定位。