航空重力测网交叉点的非遍历逼近方法

屈进红,姜作喜,周锡华,罗 锋,李 芳

1. 自然资源部航空地球物理与遥感地质重点实验室，北京 100083； 2. 中国自然资源航空物探遥感中心，北京 100083

航空重力测量以飞机为载体，融合了重力传感器、惯性系统(INS)和差分全球定位系统(DGNSS)获取近地空中重力加速度的一种动态重力测量方法[1-6]。在中、高频重力场信息方面，弥补了地面重力、卫星测高在获取重力场信息方面的不足[7-8]，具有一定的优越性。由于其动态性特点，同一观测量无法进行重复观测，因此测线上往往布设切割线形成纵横交错的网状，根据交叉点重力值的符合程度来评估某个架次的测量质量[9]，直至评价整个测区的测量精度[10-15]。不仅如此，测线间存在的重力场水平差异通过与切割线上的交叉点重力差值进行水平调整，是数据处理中的关键性步骤[16]，对数据处理和地质解释具有重要的意义[17]。交叉点不符值的搜索除用于航空重力外，还可用于船载和其他机载的地球物理场测量中，甚至卫星测高中的平叉处理也涉及轨道交叉点的获取[18-19]，研究该方法具有十分重要的意义。

航空重力测网设计密集且数据采样率高，整体数据量庞大，如果采用逐一遍历或局部遍历搜索法，求取交叉点耗时长、效率低。目前常用的交叉点搜索方法主要是跳跃搜索法[20]、主副测线斜率法[21]、坐标平均法[22]、多项式拟合法[23]、滑动窗口法[24-25]及四叉树分解法[26]等。其中，跳跃搜索法、主副测线斜率法和坐标平均法，都是根据测网计算近似交叉点，再设置一定范围内进行遍历搜索出实际交叉点。多项式拟合法通过拟合测网飞行轨迹后计算近似交叉点，再设置搜索范围后遍历搜索，准确率比前几种方法有所提高，但搜索时间变长了。滑动窗口法对上述方法进行了改进，以一定搜索范围在测线上进行滑动遍历搜索，相交到切割线后确定搜索中心再以较小的搜索半径进行遍历搜索，准确率获得了保障，但没有提高搜索效率。四叉树分解法，通过矩形窗口在测线和切割线上滑动遍历锁定相交矩形范围后，再以四叉树结构分解重合区域，自适应加密剖分出遍历范围，是一次提升遍历搜索效率的尝试，但对于大型测网交叉点的搜索效率，仍无法突破瓶颈。

针对以上几种搜索方法的不足，本文提出一种交叉点的非遍历逼近方法，不需对交叉点划出遍历范围，直接迭代逼近至交叉点。试验表明，本文方法优化了搜索过程，还满足了对不规则、非常规测网交叉点的搜索，提高了效率和准确率。

1 交叉点搜索方法

1.1 测网交叉点分析

航空重力测量布置测线和切割线相交叉的网状测网，搜索交叉点就是获取它们相交于水平面位置的坐标、场值差或其他物理量差值。在航空重力测量作业中，飞机基本保持直线飞行，受风向、人为控制不当等原因对飞行产生扰动而发生偏离航迹称为偏航。因此，测网交叉点搜索方法设计时尽量考虑到极端偏航情况。

如图1所示，假设航迹发生严重的偏航现象，A为偏航距。图1模拟给出了测线line 1—line 5与切割线tie 1可能存在的5种位置情况：①line 1与tie 1正常相交；②line 2与tie 1真实相交，但没有被切割线两个端点相交到；③line 3与tie 1不相交，但端点延伸后被相交；④line 4与tie 1不相交；⑤line 5被tie 1的端点相交到，但实际没有相交。示意图中，实际相交的只有测线line 1、line 2，测线line 3、line 5也被误相交到，后续需剔除。搜索测网交叉点的核心就是判断测线与切割线是否真正相交，如果相交则获取二者相交的准确坐标。图1中虚线外扩端点，就是为了解决因偏航可能被遗漏的实际交叉点，把所有测线和切割线端点延伸，延长量为规范中偏航阈值80 m[27]的2～3倍，确保交叉点无遗漏。

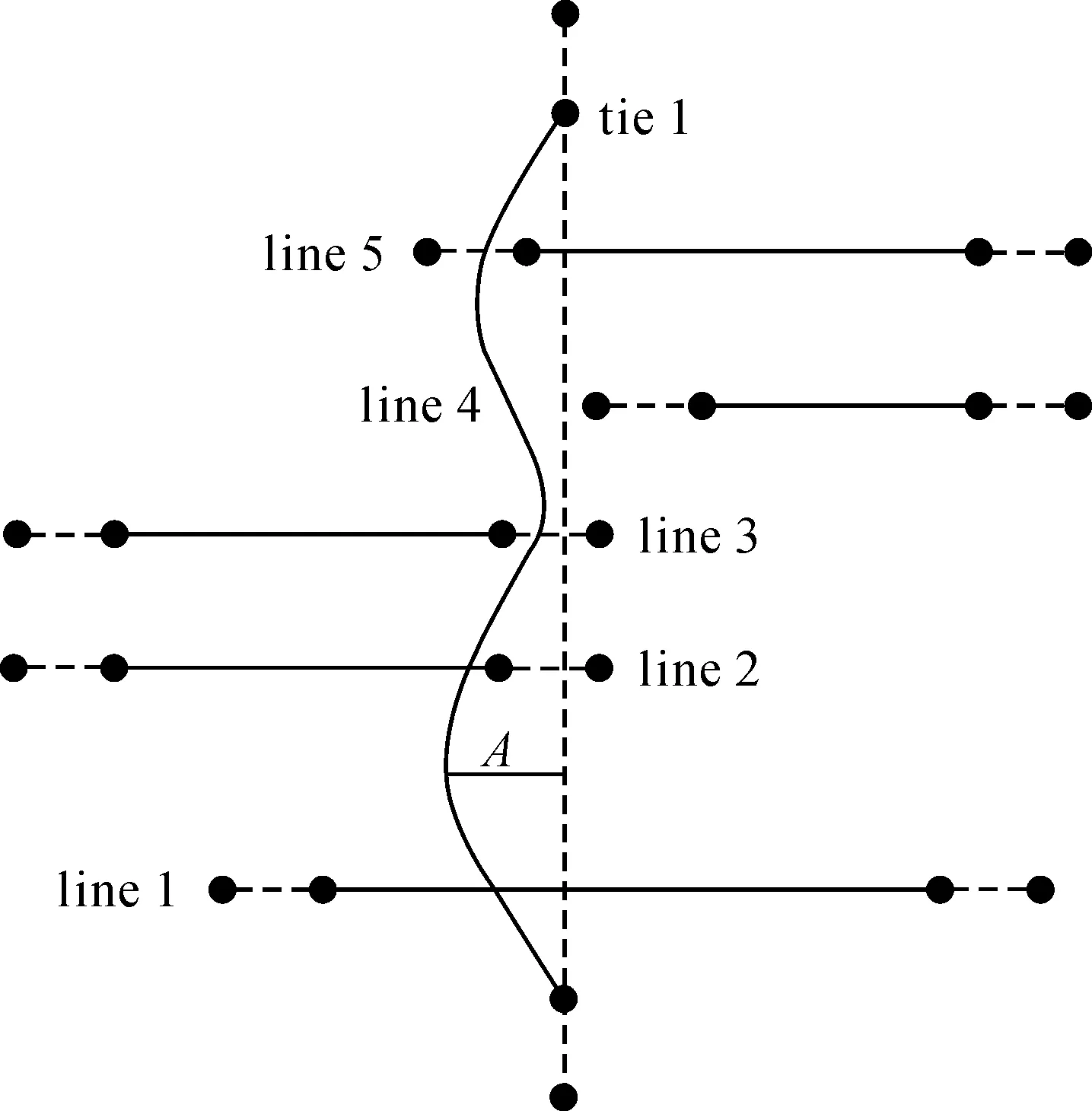
图1 测网中存在多种相交位置Fig.1 Multiple intersections at the boundary of the survey network

1.2 交叉点搜索思想

本文提出按照快速逼近和微调逼近组合思路，进行迭代式逼近交叉点的搜索方法设计算法，以最小计算量，快速准确定位交叉点。以每条测线和切割线上的平均点距为标尺进行2次或3次迭代式快速逼近后，测网中绝大部分近似交叉点无限逼近目标，只需小范围内微调逼近1～2次便能搜索到交叉点。而个别交叉点处在不均匀、不连续的测网上，平均点距误差会加大，甚至交叉点位于缺失数据的不连续测线上，所以在经过多次快速逼近后还没有落到目标测点附近时，为避免程序陷入死循环也进行微调逼近。通过组合设计既保证交叉点搜索速度，同时兼顾精准度。

本文方法对测点间距适宜、分布均匀、测网轨迹规整的测网适用性好，搜索效率越高；对测网的测点过密、不均匀，轨迹不规整等，将增加微调逼近次数，搜索效率略低。本文搜索效率统计使用逼近次数概念，如快速逼近交叉点1次代表对测线line和切割线tie各进行了1次跳跃逼近，共计2次。为提高程序执行效率，只对第1次和第2次快速逼近交叉点完成后进行判断和逼近统计。若不相交则进入微调逼近循环，只要在line或tie线上逼近1次就累计1次，直至相交结束。

1.3 交叉点相交判断方法

判断线段是否相交包括行列式、投影法和面积法等。文献[25]研究表明，3种方法的计算效率相当。本文使用了向量叉乘面积法，利用两向量叉乘等于两向量构成的平行四边形(以两向量的邻边)的面积，由于向量具有方向，所以面积也具有方向，构成三角形的面积以逆时针为正，顺时针为负，令两线段的4个端点坐标为T1(x1,y1)、T2(x2,y2)、L1(x3,y3)、L2(x4,y4)，其中x1-x4为经度，y1-y4为纬度，如图2所示。

图2 两线段的向量叉乘Fig.2 Vector cross product of two line segments

图2中两线段4个端点构成4个三角形：L1L2T1、L1L2T2、T1T2L1和T1T2L2，它们的叉乘面积按式(1)—式(4)计算

(1)

(2)

(3)

(4)

满足SL1L2T1·SL1L2T2≤0，切割线端点T1、T2被测线线段相交；不满足，则位于测线同侧。同理ST1T2L1·ST1T2L2≤0，测线端点L1、L2被切割线线段相交；不满足，则位于切割线同侧。当式(1)—式(4)同时满足上述要求时，即存在交叉点。当切割线或测线的1个端点与测线或切割线两端点处在同一条线上，此时共线下的两向量叉乘面积为0，也存在交叉点。

符合交叉点存在条件后，计算交叉点位于切割线两端点之间的位置系数α为

(5)

通过式(5)可获得交叉点坐标P(x,y)，经度x、纬度y分别为

x=x1+α(x2-x1)

(6)

y=y1+α(y2-y1)

(7)

2 交叉点计算的程序实现

2.1 程序设计

按照上述搜索方法，设计了交叉点搜索流程，如图3所示。装载测网后，对测线和切割线延伸的4个远端点组成线段后判断是否相交，存在相交后第1次获取近似交叉点坐标，再计算测线和切割线起始测点到近似交叉点的距离，根据各自的平均点距第1次快速逼近找出4个端点；若不相交接着把这4个端点再次进行线段相交，第2次获取近似交叉点坐标，重复上述过程第2次快速逼近找出4个端点；若不相交，程序进入微调逼近循环直至相交。

图3流程中，以微调逼近循环左侧为例，先以tie线段为基准，判断测线的相邻端点L1、L2是否与之相交，若不相交测线两个端点逐点向第2次近似交叉点坐标方向滑动，直至与tie线段相交；接着切割线的端点T1、T2，若不与line线段相交，两端点逐点向最新的近似交叉点坐标方向滑动，直至与line线段相交；因切割线端点的滑动，为防止发生测线端点与tie线段又不相交，再次重复上述过程，直至真正相交。而图3中的微调逼近循环右侧，则用于在快速逼近后测线的两端点已经相交于tie线段，但切测线的两端点与line线段不相交的情况，实现过程与左侧类同。在交叉点相交后，再搜索下一条测线或切割线，直至整个测网的交叉点搜索完成。程序通过快速逼近和微调逼近的组合进行迭代式逼近，搜索方法思路清晰，程序比较容易实现。

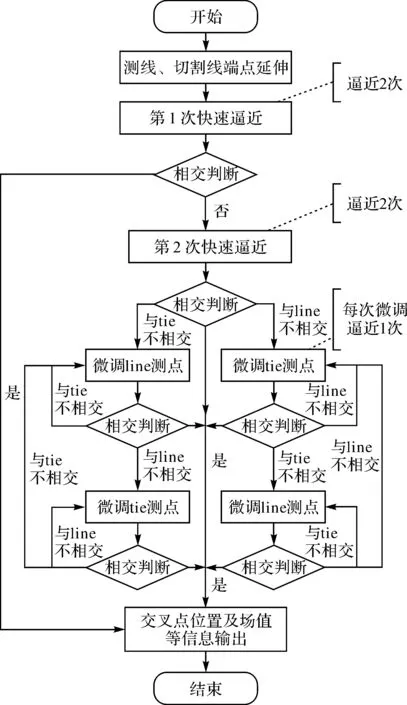
图3 交叉点搜索流程Fig.3 Flow chart of intersections searching

2.2 实例分析

2.2.1 美国大地测量局EN01测网

2013年3月美国大地测量局(National Geodetic Survey,NGS)对外发布航空重力测量EN01数据块Beta2版，此数据块国内学者研究较多[25-26，28]，包含测点号、采样时间、经度、纬度和场值，共100 830个数据点。表1给出了EN01测网的设计参数，图4为测网交叉点的分布图。

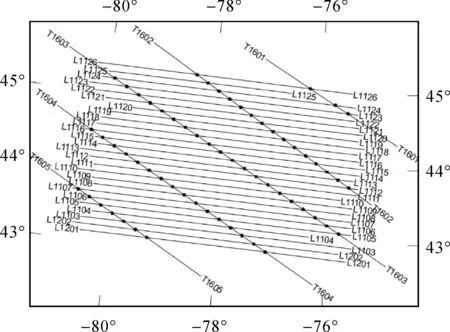
图4 EN01数据块测网及交叉点Fig.4 Survey network and cross point diagram of data block EN01

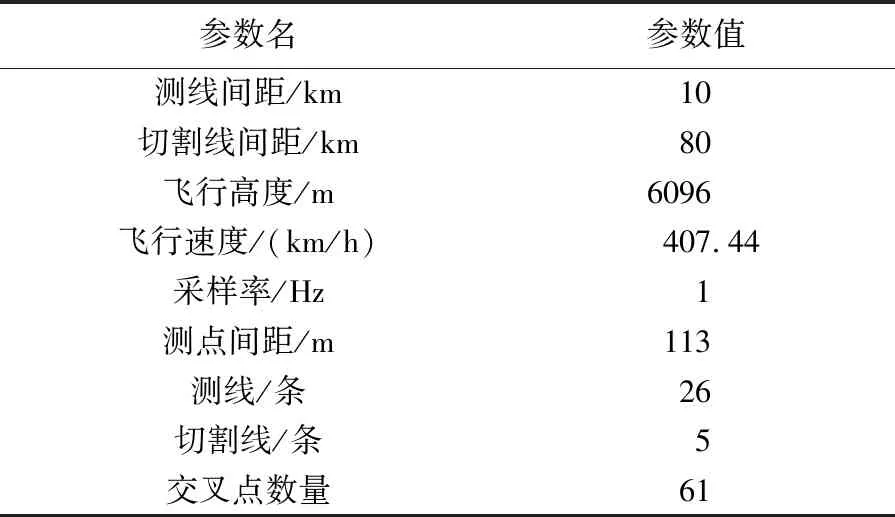
表1 EN01数据块的设计参数Tab.1 Parameters of the data block EN01

表2中给出的搜索时间对比情况，逐一遍历及优化逐一遍历法和本文搜索方法的运行环境：Intel Xeon E3-1505Mv6@3.0 GHZ，内存32 GB。其他方法的搜索时间都来自文献[25-26]，四叉树分解法使用的硬件信息：Intel Xeon E3-1230v5@3.4 GHZ，内存8 GB；其他几个方法使用的硬件信息：Intel Core i3-2350M@2.3 GHz，内存4 GB。读取和整理10万个测点用时约0.1 s，本文搜索方法比其他方法的搜索速度提升了3～4个数量级。

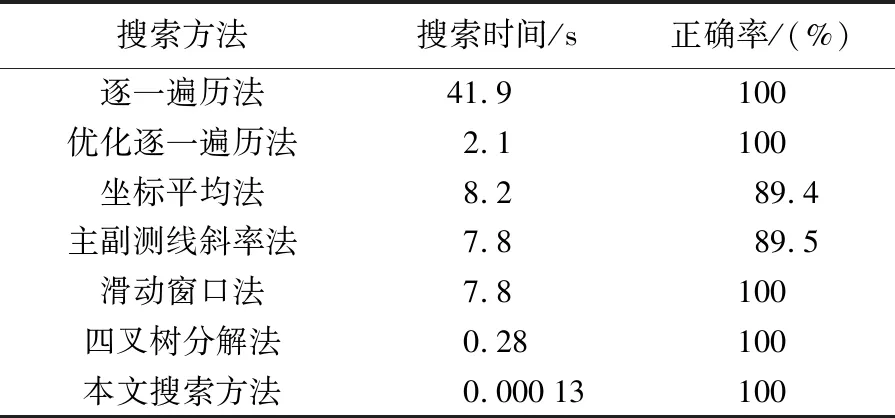
表2 EN01用不同搜索方法的统计信息Tab.2 Statistical information with different methods for EN01

2.2.2 大型测网算例

使用美国大地测量局发布的航空重力测网AS08和塔里木盆地航空重力大型拼接测网TAZB，分别包含6 135 004个测点、310个交叉点，5 466 366个测点、29 517个交叉点，利用本文方法搜索并找到全部交叉点分别用时0.031 s和0.061 s。表3列出了与成熟商业软件Oasis Montaj之间的交叉点搜索计时情况。读取和整理AS08和TAZB文件(X、Y坐标和场值)分别约5.3 s和4.9 s，在Oasis Montaj测网数据库中，没有观察到装载数据用时。

表3 与商业地球物理软件处理大型测网对比Tab.3 Compared with commercial geophysical software for large survey networks

3 交叉点搜索效率分析

3.1 快速逼近设计

根据多个测网验证，常规测网可以设计成快速逼近循环直接逼近交叉点，但交叉点处在缺失数据的不连续测网中会使程序陷入死循环，另一方面，过多使用快速逼近也会影响到搜索效率，应视测网情况合理设置快速逼近的使用频率。

取两个国内航空重力测网为例，鞍山本溪直升机起伏飞行测网ANB的平均点距和标准差为：16.17±0.97 m，对测网分别进行2～10倍加密和2～10倍抽稀，形成平均点距1.6～161.7 m的共19个不同密度的测网。程序中分别设置快速逼近2、3和4次结合微调逼近后，统计这19个测网完成交叉点搜索时所用的逼近次数，以快速逼近2次的结果进行归一化，观察快速逼近3、4次的执行情况，如图5所示。图中对平均点距在8.1 m及以上测网，设置3、4次的逼近次数归一化大于1，不如2次时的执行效率高。在平均点距8.1 m以下的加密测网，设置3、4次执行效率要好于2次，但也没有因为设置越高，执行效率被提高。

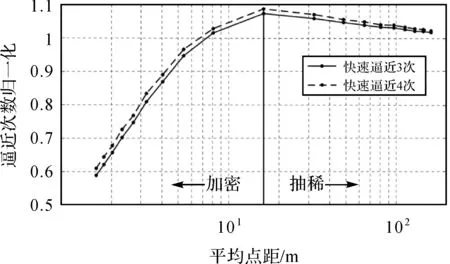
图5 测网ANB快速逼近次数归一化Fig.5 Normalized graph of fast approximation times of ANB survey network

海南岛周边固定翼飞机测网HAIN的平均点距和标准差为：31.03±0.32 m，同样进行2～10倍加密和2～10倍抽稀形成19个测网。然后进行快速逼近2、3、4次的逼近试验，以设置2次的结果进行归一化，发现设置2次时在各个测网密度中的执行效率都是最佳的，并且随着测网变疏它们之间的归一化结果趋于收敛，如图6所示。HAIN测网测点距的标准差偏小，即测点间分布比较均匀，搜索结论与ANB测网出现截然相反的现象，测网加密下没有因为增加快速逼近的次数，而提高搜索效率反而出现下降。

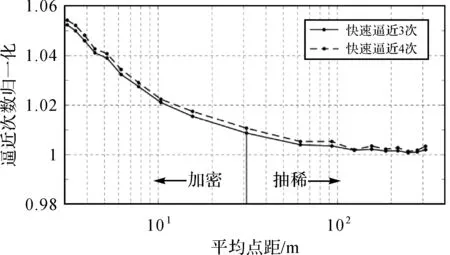
图6 测网HAIN快速逼近次数归一化Fig.6 Normalized graph of fast approximation times of HAIN survey network

对比不同情况的测网，大量的试验都得出类似结果。程序中设置成快速逼近2次和微调逼近组合，在常规测网中就可以发挥出较好的搜索效率；如果测点距标准差偏大，同时测点距小于8 m以下的测网，宜采用快速逼近3次甚至4次，再结合微调逼近进行搜索。

3.2 EN01测网搜索分析

本文逐一遍历法：从切割线起算，在测线上遍历找到交叉点后及时跳到下一条测线，计算工作量大约减半，即

(M-nL)×(N-nT)/2

式中，M为所有测线的测点数和；nL为测线条数；N为所有切割线的测点数和；nT为切割线条数。

优化逐一遍历法：对切割线相交测线的近似交叉点坐标进行排序，切割线逐点遍历时只需遍历第1条测线，找到交叉点后把它排除在外，剩余测线重新排序，以此类推。避开了大量的重复遍历，缺点是对拼接测网、重复线混叠的时候不能保证100%搜索准确率。

EN01测网的测线有83 052个测点，切割线有17 778个测点，共61个交叉点。表4中为测网交叉点的搜索效率统计，本文方法统计出每个交叉点的平均逼近次数为6.56次，比逐一遍历方式的逼近次数减少5～6个数量级，搜索速度则提升了4～5个数量级。

表4 EN01测网交叉点的搜索效率统计Tab.4 Search efficiency statistics for EN01 intersections

EN01测网中有两条测线L1122和L1124对重力扰动假异常做了切除，分别丢失319和630个测点，造成约36 km和71 km数据缺失。本文方法受这两条测线数据的不连续影响，测线中平均点距误差加大导致交叉点搜索效率下降。在剔除这两条测线后，每个交叉点平均逼近次数由原先6.56次下降到4.75次，搜索效率明显提升，详见表5。

3.3 多个测网交叉点搜索分析

表5中，美国大地测量局使用二轴阻尼稳定平台TAGS航空重力仪，因抗飞行颠簸性能差，人为切除了EN01、PN02和AS08测网中部分测线的扰动异常，从而造成测线中测点的不连续性。其中AS08测网切除了7条线的扰动异常，6个交叉点又位于剪切处，采样率为20 Hz；剔除这7条线后为AS08′测网，平均点距及标准差为6.06±0.59 m。EN01和PN02测网的采样率均为1 Hz，EN01′和PN02′为各剔除2条不连续测线后的测网。表5、表6中，除测网AS08、AS08′和YYQC使用快速逼近3次外，其余测网均使用2次，再采用微调逼近。

表5 多个测网交叉点的搜索效率统计Tab.5 Search efficiency statistics for more network intersections

测网EN01、PN02，平均点距的离散程度偏大，每个交叉点的平均逼近次数搜索效率略低；AS08测网因有6个交叉点位于不连续处，搜索效率更低。而较规则测网EN01′、PN02′、ANB、HAIN、TAZB的平均逼近次数在3.9～4.75之间；平均点距小于8 m的AS08′测网，快速逼近调高至3次后的平均逼近次数为6.64，调高至4次时没有获得提升。

某海域船载重力测网YYQC的平均点距及标准差为2.61±1.01 m，从标准差的偏离程度看出测点距比较离散或者测线之间的航行速度控制不稳定，测网的船测航迹保持也欠规整，如图7所示。使用快速逼近3次后的每个交叉点平均逼近次数为21.82，调高至4次后，平均逼近次数下降至13.13，获得明显提升。

图7 远洋船载重力测网Fig.7 Ocean-going ship gravity survey network

表6中，统计多个测网的交叉点逼近次数2～8次，分别对应交叉点搜索的完成情况。平均点距大于8 m，较规则测网中只有大型拼接测网TAZB在逼近8次后完成98.2%，测网EN01′、PN02′、ANB和HAIN都在8次逼近内完成。表5、表6中得出认识：测网测点连续性、航迹规整、平均点距大小和它的离散程度适宜，对提高交叉点的搜索效率至关重要。

表6 多个测网的逼近次数与搜索完成比例统计Tab.6 Statistics of the number of approximations and completion ratios formore survey networks

4 结 论

本文提出快速逼近和微调逼近组合进行迭代式非遍历逼近交叉点的方法，克服了常规方法进行局部遍历的不足，大幅度提升了交叉点的搜索效率和准确率。搜索速度较现有文献方法提升3～4个数量级，也远优于著名商业地球物理软件，对多个测网的应用效果十分显著。通过测网交叉点搜索效率分析得出：

(1) 针对常规航空重力测网，交叉点搜索流程中快速逼近只需设置2次，就能实现快速搜索。

(2) 测网中测点不连续或者平均点距小于8 m，且标准差偏大，建议快速逼近调升至3次，发挥出较好的搜索效率。

(3) 对于航行速度慢又不稳定，以及航迹不规整的船载重力测网，为提高搜索速度，建议快速逼近设置成4次，弥补船载测网的不足。