利用垂直重力梯度异常反演海底地形的解析方法
徐 焕,于锦海,安 邦,万晓云
1. 中国科学院计算地球动力学重点实验室,北京 100049; 2. 中国科学院大学地球与行星科学学院,北京 100049; 3. 中国地质大学(北京)土地科学与技术学院,北京 100083
海底地形和海底基岩密度可以反映出海底构造演化活动[1],可帮助探明海底矿产资源[2],此外,海底地形对于海事搜救等活动也是非常重要的,因此研究海底地形不仅有理论意义,而且有实用价值。目前,利用多波束回声测量装置直接测量海深是最好的方法,但是由于成本高、耗时长,因此,测得的海深数据比较稀疏,难以覆盖整个海洋[3]。近年来,利用海洋重力数据反演海底地形的工作日益受到重视,其原因是成本低、覆盖范围广。从目前已有的研究来看,反演海底地形主要利用重力异常和垂直重力梯度异常。
重力地质法(gravity-geologic method,GGM)[4],其原理是将海面上重力异常中的短波部分与海底地形存在着线性关系,然后在实际使用时,需要结合船测的海深数据,拟合出该线性关系,从而得到海底地形。GGM方法目前已经被广泛地应用于海底地形的反演[5-8]。事实上,GGM方法在海底较为平坦的区域是非常有效的,但对起伏较大的海底来说,反演海底地形的精度较差[9-10],因此GGM方法在应用上有一定的局限性。
频域方法源自Parker将引力位表达式进行傅里叶展开[11],给出了海面重力数据与海深之间的频率域表达式,略去海深的高阶小量后,即得频域内的线性关系,这为利用重力异常直接反演海底地形提供了理论依据。当考虑地壳的均衡补偿,Parker理论得到进一步完善,基于该理论,文献[12]反演皇帝海山链的海深,由于地形变化剧烈,海山链沿线附近精度不甚理想。文献[13]联合多源重力数据反演菲律宾海域的海底地形,精度提高30%左右。此外,文献[14]证实了在50~300 km波段范围内,海底地形与卫星测高数据之间存在高度相关性。在文献[12,14]的研究基础上,文献[15]说明了在15~160 km的波段内,海底地形和重力异常间具有线性相关的特征。因为在应用Parker理论反演海底地形时都会舍去海深二阶以上的量,所以精确度存在不确定性[16]。例如,文献[17]对比了GGM和Parker理论反演海底地形的结果后指出,GGM方法在可靠性和精度方面具有明显的优势。
作为重力数据的延伸,垂直重力梯度(vertical gravity gradient,VGG)对海底地形高频部分的敏感度超过重力本身[18-19]。文献[20]推导出长方体产生的VGG公式,该公式已在地球物理勘探方面得到了许多应用。例如,文献[21]利用重力梯度全张量数据,采用共轭梯度法反演地质体与密度,但其仅仅限于模拟计算。文献[22]采用聚焦反演方法来预测异常地质体的埋深信息。此外,文献[23]也利用该公式,计算了不规则地质异常体产生的垂直重力梯度,并将其用于评估西墨西哥Jasper海山的密度。在将VGG应用于预测海深方面,文献[24]利用SIO(scrioos institude of oceangraphy)的VGG数据,并结合船测数据来反演海底地形,例如,在南印度洋海域的反演结果与船测深度的均方根误差约为188 m。文献[25]利用VGG异常数据,顾及了Park理论中的二阶量影响和采用模拟退火法反演了海底地形,并给出其精度提高了22%的结论。
综合上述各种方法,其本质上还是利用经验公式来建立起重力数据与海底地形之间的线性关系,而这样的线性关系是随着海域的不同而变化的。为避开使用经验公式带来的影响,本文建立了一种解析的利用VGG数据来反演海底地形的方法,其原理是使用矩形分割将研究区域进行格网化,然后利用各个子矩形柱体产生的VGG表达式建立起各个分割子域的海深与该海域上VGG异常之间的函数关系,即导出了关于各个分割子域海深的观测方程组。但是在求解该观测方程组时,研究区域边界附近海深的求解易于受到区域外VGG异常的影响,即会产生边界效应,因此,如何评估边界效应的影响以及分离该影响的方法也就成了十分重要的研究课题。
为了减少边界效应的影响,本文将研究海域适当进行扩充,然后将扩充海域内的海深同时进行求解。为避免观测方程组出现奇异性,在求解观测方程组时引入了正则化参数,通过仿真计算后,确认正则化参数选取为10-3时,反演的海域下方海深具有较好的精度。在对实际海域的海底地形进行反演计算时,除了研究海域下方海底地形会对VGG产生影响外,其他的海底地形也会对VGG异常产生影响,本文将扩充海域外的海底地形对VGG的影响统称为远区影响。为了消除远区影响,本文将其视为干扰常数ε,并在求解观测方程组时对其同步进行求解。
1 理论与方法
1.1 长方体产生的垂直重力梯度
假设有一个海底长方体海山Ω(图1),其长、宽、高分别为2a、2b、H-h,其中H为Ω底部至海平面的高度,h为Ω顶部至海平面的高度(即Ω的海深)。记R是Ω在海面对应的海域, 显然确定Ω的形状仅需求解h。假设P是在海平面上任意一点,下面计算Ω在P处产生的VGG。
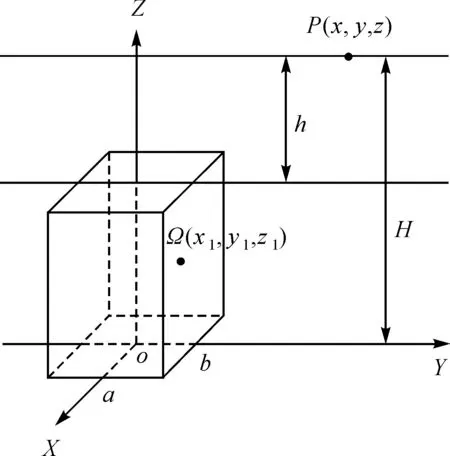
图1 长方体海山 Fig.1 Schematic diagram of synthetic cylindrical seamount
建立图1所示的坐标系,则Ω在P点产生的重力位为
(1)
式中,G是万有引力常数(6.672×10-11Nm2kg-2);ρ=2700 kg/m3是海山Ω的密度;(x1,y1,z1)为积分变量。因此,海山Ω在P点产生的VGG为
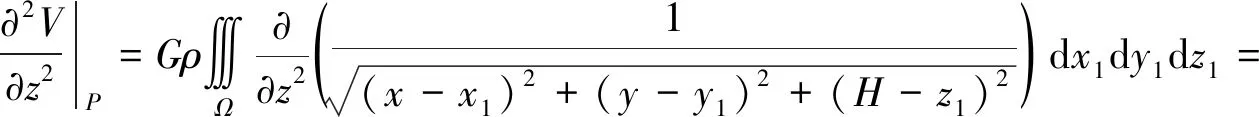
Gρ[IR(H,x,y)-IR(h,x,y)]
(2)
式中
(3)
积分区间R={(x1,y1);-a≤x1≤a,-b≤y1≤b}为矩形区间,进一步计算后可得IR(H,x,y)的表达式为
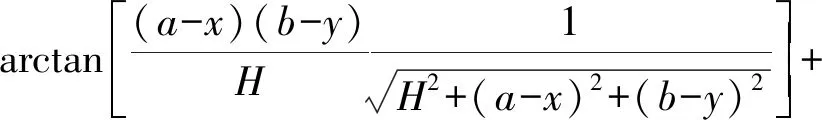
(4)
对于一般的矩形积分区间R={(x1,y1);-a≤|x1-x0|≤a,-b≤|y1-y0|≤b},结合式(4),IR(H,x,y)可写为
IR(H,x,y)=I(a,b,H,x-x0,y-y0)
(5)
同理,式(2)中的IR(h,x,y)与IR(H,x,y)有相同的表达形式。因此,得到了矩形海山Ω在海平面上任何一点P产生垂直重力梯度的表达式。
1.2 观测方程与可解性分析
为了讨论方便,下面恒设R={(x,y);-a≤x,y≤a}是海面上一个正方形区域,Ω是R下方对应的海山,其密度为常数ρ,形状为Ω={(x,y,z);(x,y)∈R,H-h(x,y)≤z≤H},其中h(x,y)是Ω的顶部至海面的高,因此,要确定R下方的海底地形就是确定函数h(x,y)。本节将在R上VGG异常仅是由Ω产生的前提下来研究如何求解h(x,y)。
选择一个步长t,将区间[-a,a]进行2N等分,即a=N·t,这样就能将区域R进行格网化,其中典型的子格网区域是Rij=[xi,xi+1]×[yj,yj+1],xi=it,yj=jt,i,j=-N,…,0,…N-1。若步长t足够小,在Rij中h(x,y)可以被看成是常数hij,于是,利用式(4)、式(5)和叠加原理可知,由Ω生成的VGG在海面P(x,y)处的值Γ(x,y)为
Γ(x,y)=
(6)
在式(6)中去掉海水的影响,则得Ω在海面上P处产生的VGG异常为
δΓ(x,y)=
(7)
式中,Δρ=ρ-ρ0,而ρ0表示海水密度,在后面的计算中总是取ρ0=1030 kg/m3。
如果事先能够给出海域R上的VGG异常的观测值,例如在R的所有格网点上VGG异常是已知的,可得
δΓ(xp,yq)=G·Δρ[IR(H,xp,yq)-
(8)

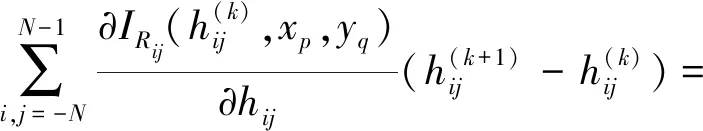
-δΓ(xp,yq)+GΔρIR(H,xp,yq)-
(9)
式(9)就是线性化后的海底深度与VGG异常之间的观测方程组。
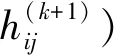
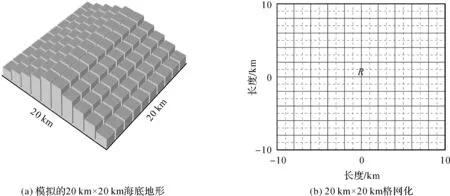
图2 模拟20 km×20 km海底地形及对应格网Fig.2 The simulated 20 km×20 km seafloor topography and corresponding grid diagram
1.3 观测方程组抗误差干扰分析
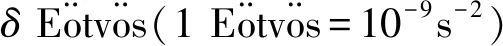
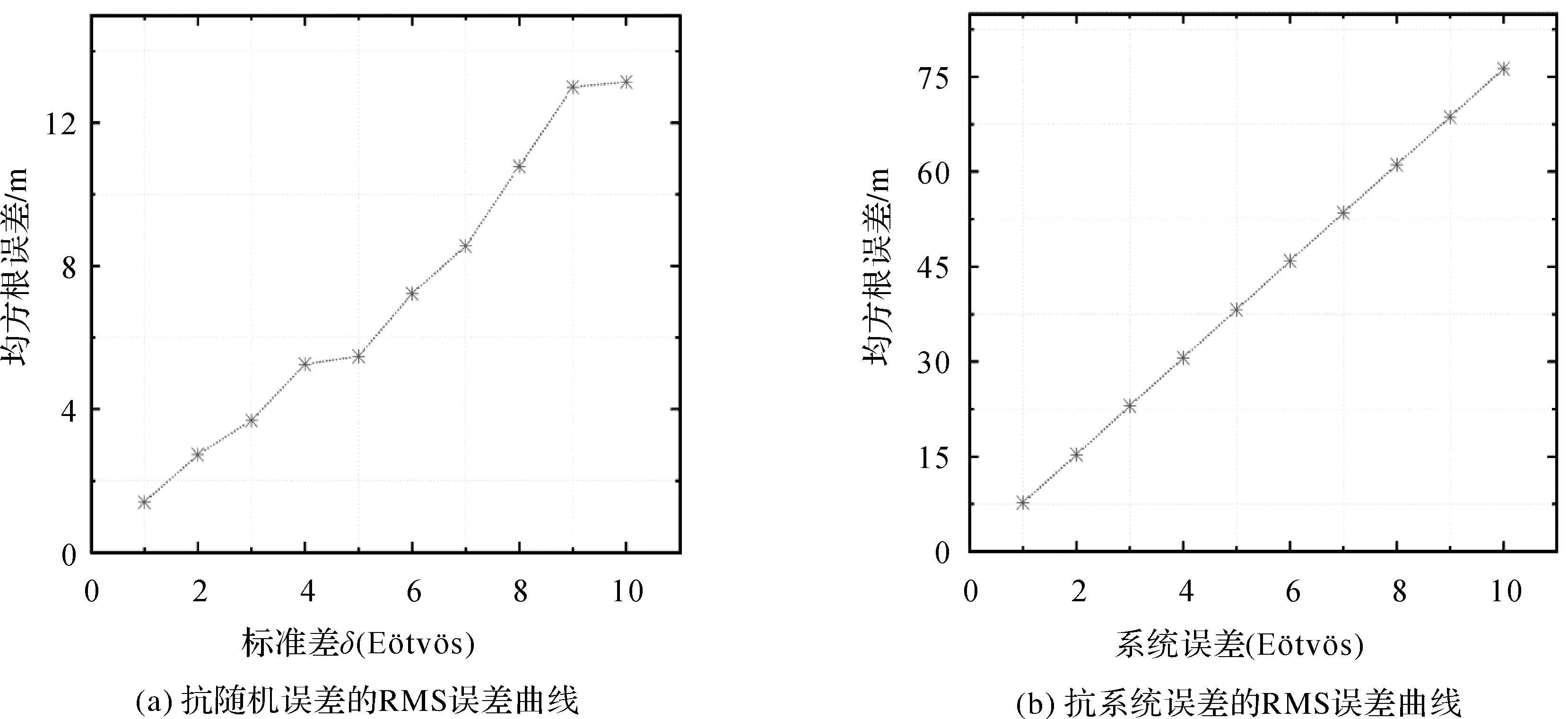
图3 抗随机误差和系统误差的曲线图Fig.3 The graph of the RMS error of the random error and the system error
2 边界效应的处理
上文建立的关于海深的观测方程式(8)或式(9)都是在海底仅有一个异常海山的前提下导出的,当处理实际海域时,显然海域下方的情况要复杂得多,特别是还存在着其他的异常海山。例如,图4(a)模拟了40 km×40 km海域D下方的海山,如果仅需要求解中心20 km×20 km区域(称为内区R)下方的海底地形,显然在内区外的海山会对内区R上的VGG异常δΓ有贡献,因此,式(8)或式(9)需要进行调整。本节主要以图4(a)模拟的海山为例来介绍求解方法和进行结果分析。
以后称40 km×40 km区域D为内区R的扩展区域,选取步长t=2 km对D进行格网化(图4(b))。称D-R为内区R的边界区域,其下方海山对内区R上VGG异常的贡献称为R的边界效应。假设在内区R上给出了VGG异常值(包含了边界效应),本文的做法是:使用内区R上给出的VGG异常值来求解出整个扩展海域D下方的海底地形,然后剔除D-R下方的海山,仅取R下方海山作为最终的反演结果。注意:采用的已知数据仅是内区R上给出了VGG异常值。

图4 模拟40 km×40 km海底地形及对应格网化Fig.4 The simulated 40 km×40 km seafloor topography and corresponding grid diagram
事实上,在式(7)中将区域取为D,而将P(x,y)点仅限于R中,则有
δΓ(x,y)=G·Δρ[ID(H,x,y)-
(10)

(11)

(ATA+αE)h=ATb
(12)
这里E是单位矩阵,α>0是正则化参数(其单位为10-24m-2s-4)。
因为α>0,所以形如式(12)的方程关于h总是存在唯一解。因此通过迭代求解式(12)的方程组后,便能从式(11)解得所有的hij(i,j=-20,-19,…,18,19)。从中选择出hij(i,j=-10,-9,…,8,9),便可得R的子分割Rij的平均海深hij。关于正则化参数α的选择,本文以得到的Rij下方平均海深hij的RMS误差作为标准,绘制了相应的曲线(图5)。
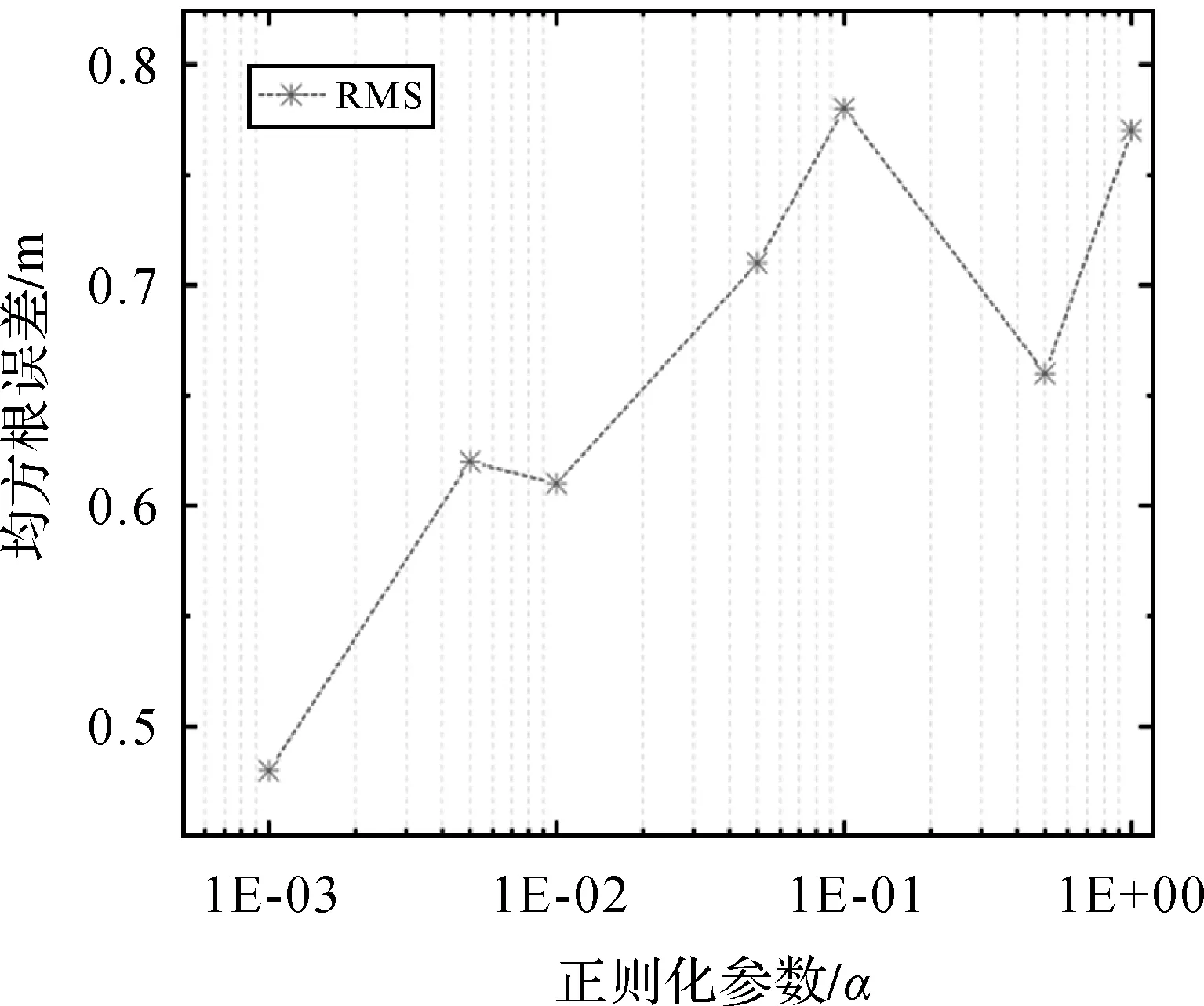
图5 不同正则化参数α对应的反演结果的RMS误差Fig.5 The RMS error of the results corresponding to different regularization coefficients α
由图5可知,当正则化参数α=10-3时海深hij的RMS误差达到最小,此时在内区R上恢复的海深的误差分布由图6给出。由图6可知,最大误差为0.64 m,RMS误差为0.48 m。因此通过将内区R扩充到D,并引入正则化参数,就可以有效地处理D-R下方海山引起的边界效应。

图6 考虑边界效应后,反演的内区下方海底地形的误差分布Fig.6 The error distribution of the inverted seabed beneath R after introducing boundary effect
3 远区海山的影响
如果选定了内区R,通过适当扩充R得到扩展区域D,就可以求解R下方海底地形的边界效应。事实上,在扩展区域D外部的下方仍有海山会对R上的VGG值产生影响,本文称这样的影响为远区影响。尽管远区影响总体来看在R上是低频的,但其对R下方海底地形的反演到底影响到何种程度是需要探讨的。本节将在上节基础上,通过引入远区海山来进一步地分析远区影响及处理方法。

图7 沿y=0,从D的左边起算的Ω生成的VGG异常的图像Fig.7 Along y=0, the graph of VGG anomalies generated by Ω from the left of D
如果将远区影响看成是R上VGG异常的系统误差,则可直接使用本文处理边界效应的方法来反演R下方海底地形。增加远区影响Ω后,其反演结果的误差分布由图8(a)给出。从图8(a)可知,受Ω影响,反演的内区R下方的海底地形的最大与RMS误差分别是71.8 m与39.4 m。
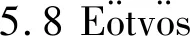
在处理实际海域问题时,一旦选定了内区,其远区影响是非常大的,这是因为实际的远区影响是由多种因素产生的。例如:除了本文描述的扩展区域外海山的影响外,还存在着地球深部质量分布不均匀等因素的影响。如果相对于内区R来说,远区影响太大,则观测方程组(11)中会出现很大的误差项,这将会导致反演结果完全不正确。因此,必须选择某种途径去处理远区影响。
尽管远区影响的量级会很大,但是在R上VGG异常会表现出低频的特征,其理由是远区影响距内区R相对较远,而VGG自身在离开异常体后会表现出衰减很快。因此,本文将引入一个常数ε来表示R的远区影响,将式(11)改写为

(13)
然后在式(13)中同时对hij和ε进行求解。至于如何求解式(13),仍然采用对hij进行线性化,再使用正则化参数的方法来迭代解算hij和ε。
按照上面的方法,对Ω的远区影响问题进行了计算,反演得到了内区R下方的海底地形,其误差分布由图8(b)给出,其中最大与均方根误差分别是58.7 m与32.5 m。相较于图8(a)的结果,最大误差和均方根误差分别降低18.2%和17.5%。这说明加入远区影响项ε后,确实是可以消除部分远区影响的。
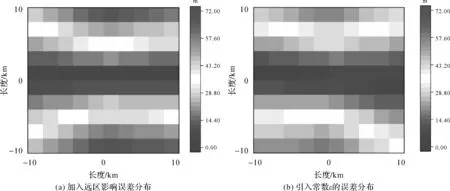
图8 考虑远区影响Ω后的反演结果误差分布Fig.8 The error distribution of the inverted seabed topography with the disturbance seamount Ω
4 实际算例及分析
前面各节分别讨论了单个海山、周边海山(边界效应)、远区海山(远区影响)等情况下如何反演某研究海域R下方海底地形的反演方法。本节将选取某个实际海域作为研究对象,来反演其下方的海底地形。这里选取南中国海72 km×72 km的海域(112.6°E~113.25°E,11.0°N~11.65°N)作为研究对象,密度差Δρ=ρ-ρ0选取为1670 kg/m3。此外,根据已有的海深数据,选择H=4.4 km。
首先在72 km×72 km的海域D中选择内部52 km×52 km海域R作为内区,其上的VGG异常数据(图9(a))来自GFZ。然后选择步长t=2 km,由此便可以建立方程式(13),对hij进行线性化,引入正则化参数α=10-3,迭代后便能解出R的子分割Rij的平均海深hij。最后将海深hij置于Rij的中心,便可生成R下方的海底地形如图10所示。

图9 VGG异常分布及船测数据点分布Fig.9 The distribution of VGG anomalies and the distribution of bathymetric points
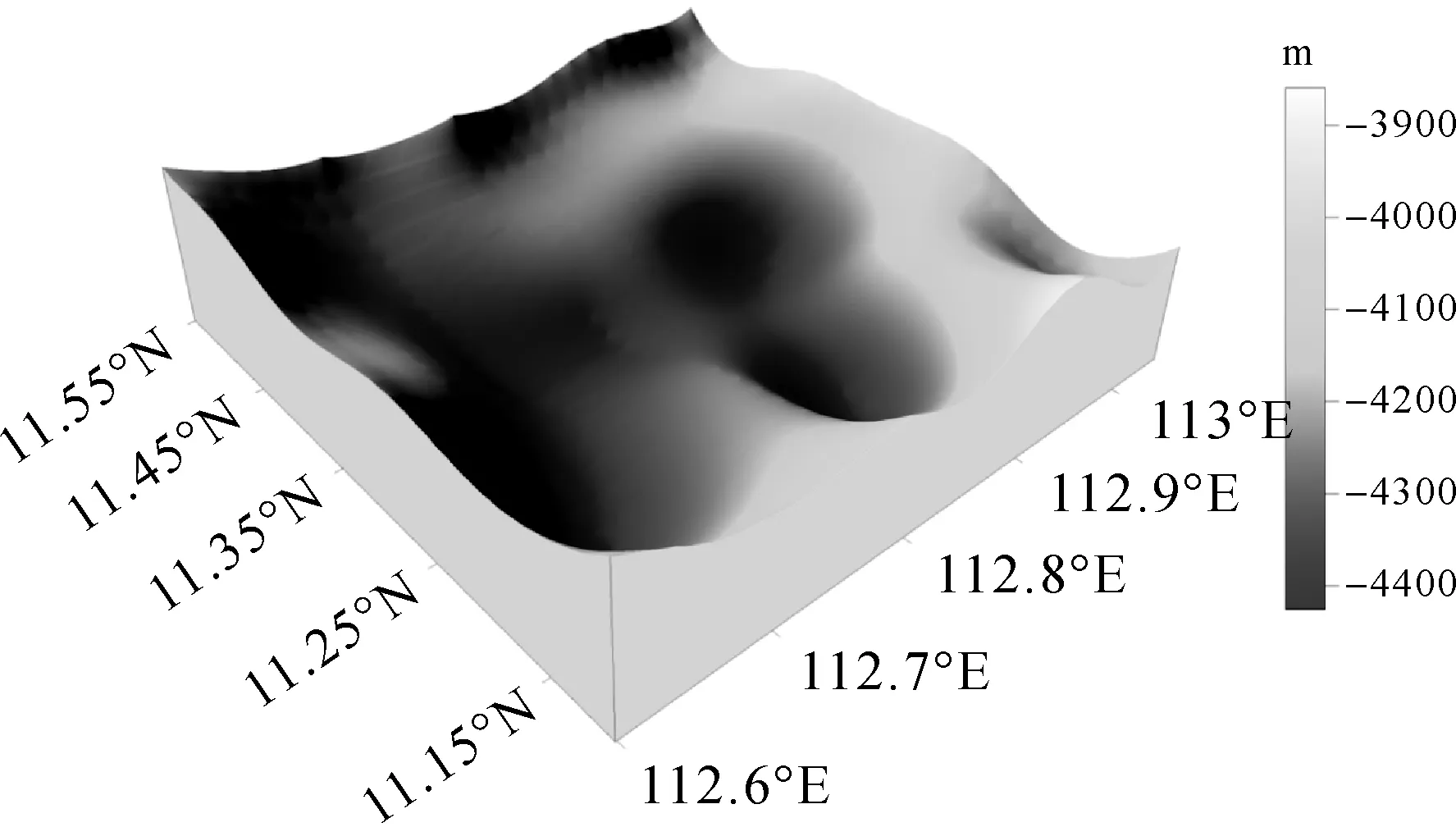
图10 利用VGG异常反演海底地形的最终结果Fig.10 The final result of seafloor topography inversion using VGG anomalies
为了检验反演出的R下方的海底地形的精度,本文选取了该海域全部289个来自NGDC(National Geophysical Data Center)船测点的海深数据,其分布由图9(b)给出。将本文反演结果与NGDC数据进行比较后可知:其最大、最小和均方根误差分别为339、-157和109 m。统计反演结果的平均深度为4173 m,均方根误差相当于平均深度的2.6%(109 m/4173 m)。另外,289个点上的误差绝对值统计见表1,结果表明:误差主要集中在150 m以下,占比为84.1%,误差大于150 m的点,占比为15.9%,且这部分点主要分布于R的边缘处。如若将最终的反演结果再向内收缩一个格网,即2 km,反演结果的最大误差和均方根误差将分别下降为207 m和99 m,同比分别下降38.9%和9.2%。

表1 反演结果误差统计Tab.1 Inversion results errors
5 总结与讨论
目前,研究重力场与海底地形的关系主要还是使用经验公式,即,通过部分实测的海深数据来拟合出海底地形与测高、重力和重力梯度等数据之间的线性关系,以此来进一步地推算海域的海底地形。显然,这样的算法是随着海域的不同而变化的。本文工作则是依靠建立起的海底地形与VGG异常之间的严格函数关系(或观测方程组)而展开的,理论上看,本文工作是解析的方法。本文:①通过在观测方程组中加入随机误差和系统误差后,进行模拟计算,结果表明观测方程组具有极强的抗误差干扰特征;②为了处理边界效应,引入了扩充区域,并在求解线性化方程组时,引入正则化参数,确保了线性化方程组的可解性,同时经模拟计算表明由此解算的海底地形具有很高的精度,统计出的均方根误差为0.48 m;③分析了远区影响对反演结果的影响,使用某个常数来吸收远区影响,这样就能确保远区影响较大时,观测方程组依然有很好的可解性;④将本文的理论方法用于实际海域中,并得到统计的均方根误差为109 m的海底地形反演结果,从而验证了本文方法的有效性。
本文对海域格网化时,采用的步长为2 km,即在2 km×2 km范围内,仅使用平均海深来表示海山,这意味着在2 km范围内海底地形的起伏是难以分辨出来的。如果将步长取得更小,理论上讲对海山的解算精度也会增加,但是重力场数据的分辨率会制约步长的选择。例如,EGM2008重力场模型的阶次是2160[26],其空间分辨率约为8 km,如果步长小于4 km,那么来自EGM2008模型的重力数据是不能反映出4 km×4 km内的地形起伏的。因此,处理实际问题时,步长的选择与重力数据的分辨率是相关的。基于此,若要提高海底地形的反演精度,不仅要提高重力数据的精度,而且还需要提高数据的分辨率。
本文主要的研究内容还是侧重于理论与方法上,即针对建立的从垂直重力梯度数据反演海底深度的观测方程组,进行抗误差性分析以及处理边界效应等分析、验证。因此,在对实际海底地形进行预测时,都将海山和海水密度取成了常用的推荐值。事实上,在实际预测海底地形时,应该尽可能地参考当地的地质与海洋资料来选择海山与海水的密度分布。
致谢:感谢GFZ和NGDC提供的计算数据。

