深度梯度下降森林模型在轴承故障诊断中的应用

彭启明，邵 星，，王翠香，皋 军

（1.盐城工学院 机械工程学院；2.盐城工学院信息工程学院，江苏盐城 224051）

0 引言

轴承是机械设备的核心部件，直接关系其性能发挥。轴承故障轻则导致整机失效，降低生产效率，重则导致人员伤亡。轴承故障诊断可根据诊断结果及时提出解决方案，保证机械正常运行，减少或消除机械故障事故。现阶段主流的轴承故障诊断方法分为基于特征工程的方法和基于深度学习的方法两种。基于特征工程的方法主要通过对输入信号进行频谱分析（Frequency Analysis）、经验模态分析（Empirical Mode Decomposition，EMD）、小波变换（Wavelet Transform，WT）等处理后提取得到特征，再使用基于机器学习的分类模型，如人工神经网络（Artificial Neural Networks，ANN）、支持向量机（Support Vector Machine，SVM）、隐马尔可夫模型（Hidden Markov Model，HMM）等对特征进行分类故障诊断。该类方法的特征提取与分类诊断过程分离，过度依赖人工经验，误差较大。深度学习由于其强大的特征提取能力和端到端的学习特点，能够直接从原始轴承信号数据中提取故障特征并进行分类诊断，打破了特征工程方法的局限性，使得大量学者对其进行深入研究。例如，Tamilselvan 等提出了一种基于深度置信网络的故障诊断方法，打开了深度学习在故障诊断领域应用的大门，证实了基于深度学习的故障诊断方法的优势；Lu 等提出一种基于卷积神经网络（CNN）的轴承故障诊断方法，虽然具有较高的诊断精度，但模型不够稳定；Zhang 等提出一种一维CNN 的深度学习模型，可以直接对轴承信号进行故障诊断，但该模型需要大量数据进行前期学习；曲建岭等提出一种无需手动提取特征的CNN，但其训练超参数过多，导致训练和诊断成本过高；李嫄源等提出一种SVM 与PSO 相结合的电机轴承故障诊断方法，但针对复杂的轴承分类问题容易陷入过拟合且泛化能力较差；宮文峰等提出一种改进CNN 的轴承故障诊断方法，准确率达99.04%，但无法在小数据集上进行诊断。由于轴承大多时候处于正常运转状态，真实故障数据样本难以大量获取，上述基于深度学习的轴承故障诊断方法虽然在一定条件下可取得较好效果，但在小样本、低开销的情况下，模型的稳定性、泛化性、鲁棒性仍需进一步提升。

深度森林（Deep Forest）模型在小规模数据集上的性能优于其他深度学习模型，且其超参数较少、计算开销较小。因此，本文基于深度森林模型，提出一种深度梯度下降森林（Deep SGD-Forest，DSGDF）模型用于轴承故障诊断。实验结果表明，该模型不仅继承了深度森林模型鲁棒性强、泛化性好、超参数较少等优点，还避免了级联结构收敛速度慢的缺陷，实现了小样本条件下高精度、低开销的有效诊断。

1 算法模型

1.1 深度森林模型

2017 年，Zhou 等首次提出深度森林模型，该模型由级联森林结构与多粒度扫描结构两部分组成，核心思想为对随机森林算法进行集成。其借鉴了深度神经网络（Deep Neural Network，DNN）中的逐层结构（Layer-by-Layer），对前一层输入的样本数据和输出结果数据进行拼接操作后作为下一层的输入数据。深度森林模型结构简单、计算开销小，模型复杂度可自适应伸缩，具有较强的鲁棒性，在金融、医学、交通运输、军事等领域均有应用，且针对不同数据类型均取得了较好的实验效果。

1.2 DSGDF 模型

DSGDF 模型是基于深度森林模型改进而来，在继承了深度森林较少超参数、小样本学习、鲁棒性强、泛化性好等优点的基础上，通过集成梯度下降算法改善了级联结构收敛速度慢的问题，使得计算和优化开销变小。

1.2.1 梯度下降算法

梯度下降算法是一种优化算法，其在训练数据时具有降低模型损失、提高训练速度和算法收敛速度等优点，表示为：

式中，

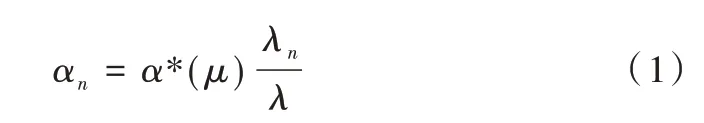
α

为第n 次迭代学习率，α 为首次学习率，

μ

为衰减率，

λ

为第

n

次迭代学习步数，

λ

为总学习步数。

1.2.2 多粒度扫描结构

多粒度扫描是增强表征学习能力的结构。原始样本数据通过不同尺度的小窗口进行扫描，从而实现特征转换，最终得到具有多样性的表征向量。

为应对轴承数据的固有特点，本文采用序列扫描的方式，过程如图1 所示。原始输入为

A

dim 样本，使用

B

dim、步长为1 的小窗口进行滑动采样。通过一系列特征转换后得到

C

=(

A

-

B

)∕1+1个

B

dim 特征子样本向量。将其送入梯度下降森林和完全随机森林中训练后得到每个森林的一个

C

*

E

的表征向量，最后将图中每层森林产生的表征向量拼接在一起，得到最终样本输出并送入级联森林结构中进行运算。

1.2.3 级联森林结构

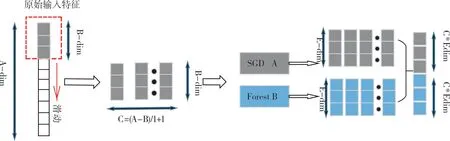
Fig.1 Multi-grained scanning process of mechanical bearing data图1 机械轴承数据多粒度扫描过程

Fig.2 Comparison of DSGDF model and deep forest model图2 深度梯度下降森林模型与深度森林模型比较

式中，

k

指

k

个类别，

p

为第

k

个类别的概率，

Gini

(

p

)为基尼系数。

基尼系数为该节点的判别依据，直到每个叶子节点只包含同一类实例后停止运算。然而，相关实验表明级联森林的收敛速度较慢。针对该问题，DSGDF 模型集成梯度下降算法，使级联森林的每一层都由5个完全随机森林和5个梯度下降算法组成，如图2 右所示。为防止最后产生的结果发生过拟合现象，需经过K 折交叉验证处理后输入到下一层。当级联森林结构扩展到新的层级后，之前所有级联结构的效果将通过验证集评估，当评估结果无法得到进一步提升时则会自动结束训练过程。因此，级联森林结构的层数与复杂度由训练过程自动确定，省去了大量调参的开销，提高了收敛速度，可使其结构保持稳定收敛状态。

1.2.4 算法实现步骤

输入训练集T，测试集S，验证集M，N 为森林中子树数目，T1 为多粒度扫描后的训练集。具体算法步骤为：

2 轴承故障诊断实验数据处理

2.1 轴承数据集来源

采用凯斯西储大学轴承数据集，其数据客观、可信度高，是轴承故障诊断领域公认的标准数据集。该数据集是以电机、转矩传感器、功率计、16 通道数据记录仪、6203-2RS JEM SKF∕NTN 深沟球轴承以及电子控制设备为实验器械，使用电火花加工技术人为制造出轴承的故障数据，包含驱动端加速度数据、风扇端加速度数据、基本加速度数据和时间序列数据。具体参数：轴承直径包括0.007、0.014、0.021 英尺，电机负载包括0、1、2、3 马力，电机转速包括1 797、1 772、1 750、1 730rpm（转∕分），还包括轴承内圈、外圈、滚动体3 点钟（直接位于受载区）、6 点钟（正交与受载区）、12 点钟（相对于受载区）方向，数字信号采样频率为12KHz、48KHz 的故障数据集以及各类各方向轴承的健康数据集。

2.2 轴承故障诊断流程

基于DSGDF 的轴承故障诊断流程如图3 所示。

步骤1：使用凯斯西储大学轴承数据集中采样频率为12KHz，电机负载分别为0、1、2 马力，故障直径分别为0.007、0.014、0.021 英尺，6 点钟方向的轴承内圈、外圈、滚动体风扇端产生的9 组加速度故障数据，以及相对应的1组轴承健康数据，共计10 组数据，10个样本特征，约300 万个数据点样本，具体如表1 所示。

Fig.3 Bearing fault diagnosis process based on DSGDF图3 基于DSGDF 的轴承故障方法诊断流程

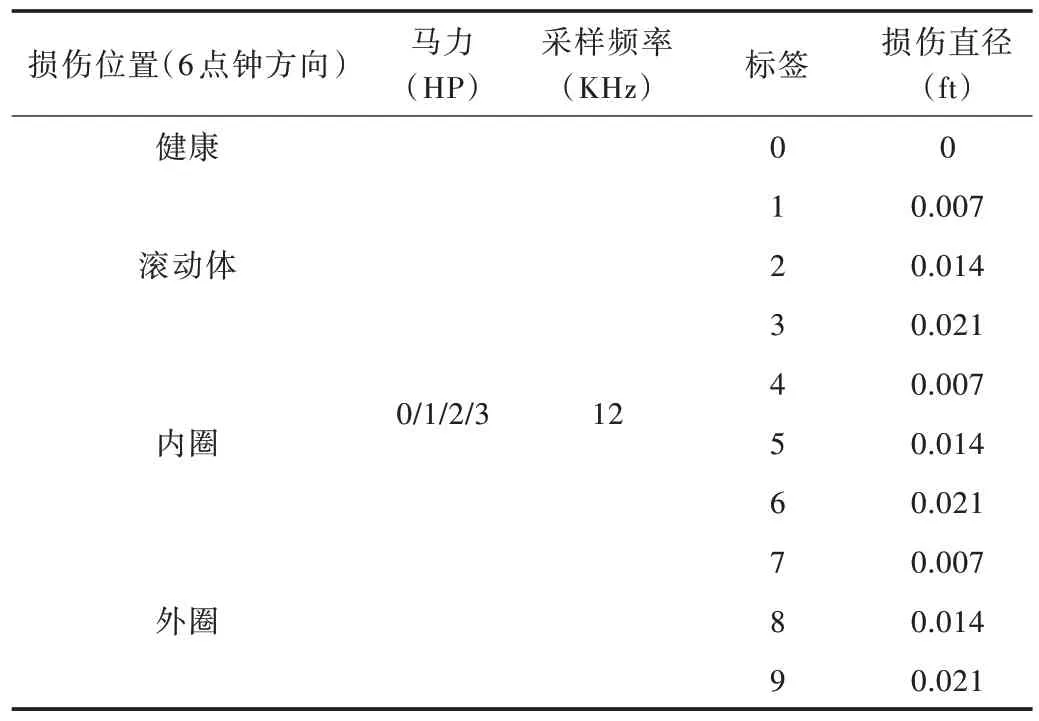
Table 1 Experimental data set表1 实验数据集

步骤2：对轴承健康数据集进行数据增强和降采样处理，数据增强滑动窗口时间长度设置为2 048∕12 000，数据重叠部分比例为50%。将轴承健康数据增强为其他故障数据的2 倍，再对其进行降采样、随机删减，以防止因故障、健康数据不平衡而陷入局部最优诊断。然后对所有数据进行归一化和独热编码，得到有标签的数据样本，并按照7∶2∶1 的比例划分训练集、测试集和验证集。最终得到数据增强和0 类数据采样58 577 条，单个数据长度为2 048个采样点，重叠量为2 047，采样点类别数目为：［（0，5 864），（1，5 822），（2，5 850），（3，5 864），（4，5 857），（5，5 850），（6，5 878），（7，5 885），（8，5 850），（9，5 857）］。

步骤3：输入训练集至DSGDF 的多粒度扫描结构，步长设置为1。通过一系列特征转换后将产生的表征向量拼接在一起，送入级联结构进行学习。

步骤4：设置级联结构中每层梯度下降森林和完全随机森林的森林数为5，完全随机森林中子树数目为80，计算当前子树的故障诊断效果并通过投票的方式选出每个森林的最优诊断结果。

步骤5：分别计算当前一层级联结构在训练集上的故障诊断率，模型在验证集上自动评估是否需要扩展下一层级联结构，若需要则返回步骤4，若不需要则立即停止训练。

步骤6：在所有扩展层中找出训练集上诊断率最高的一层作为训练集的最终诊断结果，模型学习结束。

步骤7：将测试集输入至DSGDF 模型，循环步骤3-5，在所有扩展层中找出测试集上诊断率最高的一层，并输出该层的诊断结果作为最终轴承故障诊断率。

3 实验方法与结果分析

3.1 实验平台

计算机硬件配置：Intel（R）Core（TM）i7-6700，3.40GHz处理器，16GB 内存，8 核CPU。

计算机软件配置：Windows7 X64 位操作系统，Pycharm操作平台，Python3.5。

3.2 主要参数

如表2 所示，在级联森林结构部分设置5个梯度下降算法和5个完全随机森林，其中每个森林内存在80 颗决策树，采用2 与10 折交叉验证。在多粒度扫描结构部分设定扫描窗口大小为4，数据切片步长为1，决策树数量为101颗，每个节点的最小样本数设置为0.1。

Table 2 Construction parameters of DSGDF表2 DSGDF 模型搭建参数

3.3 结果分析

3.3.1 稳定性、泛化性分析

为确保所得数据的准确性与合理性，本文实验均重复进行10 次后取平均值作为最终结果。基于特征工程的方法采用文献［23］的特征提取方法后使用机器学习模型，如K 近邻算法模型（KNN）、随机森林算法模型（RF）、决策树算法模型（DT）、朴素贝叶斯多项式算法模型（Bayes）进行分类诊断；基于深度学习的方法，如卷积神经网络算法模型（CNN）、长短期记忆人工神经网络（LSTM）、经典深度森林模型（DF）和深度梯度下降森林模型（D-SGDF）直接自动提取特征后进行分类诊断。

将轴承数据集中0 马力负载下的9 类故障样本、1 类健康样本按照7∶2∶1 的比例划分成训练集、测试集和验证集，采用F1 值进行模型的鲁棒性验证，计算方式为：

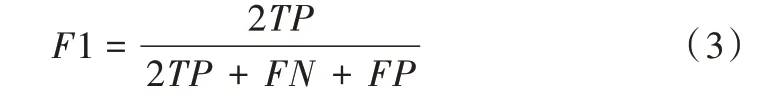
F

1 值为精度与召回率的均值，其值为1 时最佳，值为0时最差，越接近1 说明该诊断模型越稳健。评价标准见表3。

Table 3 F1-score evaluation index parameter表3 F1-Score 评价指标参数

由图4 可知，RF 模型在基于特征工程的方法中表现最好，F1 值为0.8，但仍低于基于深度学习的方法。而DSGDF模型凭借其强大的特征提取能力与基于梯度下降树的原理在10 种不同数据集诊断中F1 值均在0.98 以上，说明该模型稳定性强，鲁棒性好，能适应复杂的轴承故障诊断。

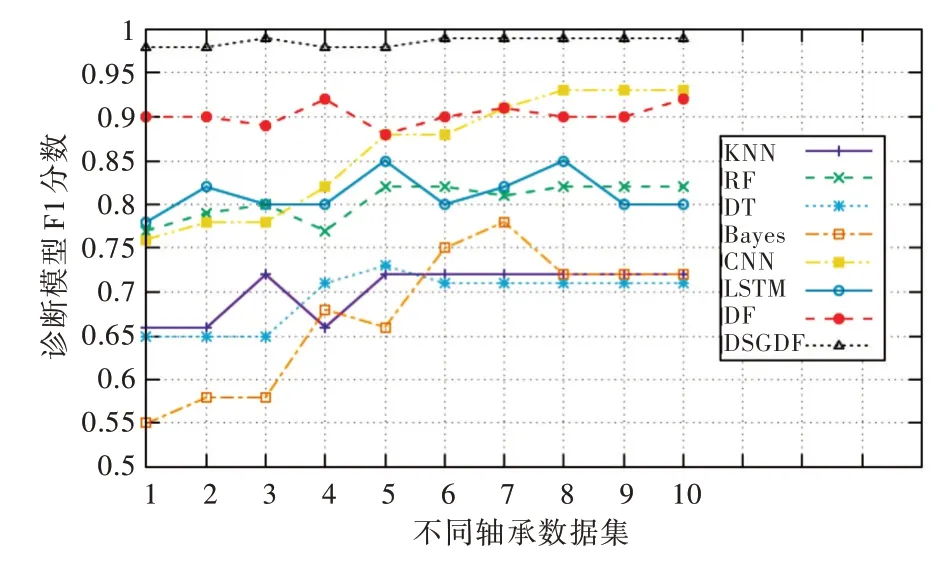
Fig.4 F1 scores of various diagnostic models comparison图4 各类诊断模型F1 值比较

在实际的机械设备运行中，轴承负载不一。为准确验证DSGDF 模型的泛化性能，分别采用0、1、2 马力负载下的轴承数据集进行故障诊断，验证其在不同负载工况下的故障诊断能力。故障诊断正确率如表4 所示。

由表4 可知，DSGDF 模型对轴承故障诊断的平均正确率为99.35%。为进一步验证该模型在其他负载条件下的泛化能力，引入负载为1 马力、2 马力的轴承数据集，进行与0 马力相同配置的故障诊断试验。结果表明，在1 马力、2马力负载状况下，DSGDF 模型的平均故障诊断正确率均达99%以上，具有良好的泛化能力。

3.3.2 故障诊断效果与开销验证

选取0 马力负载下，采样频率为12KHz，轴承内圈、外圈、滚动体风扇端加速度的9 组故障数据以及相对应的1组轴承健康数据，共10 组数据，10个样本特征，约300 万个数据点样本。数据预处理按照“2.2”节步骤2 进行，得到级联结构在训练集上的学习效果如图5 所示。可以看出，DSGDF 模型在50 次训练时准确率达90%以上，在约160 次训练时准确率达99.58%且收敛维持稳定的学习效果。该模型在测试集上的最终诊断效果如图6 所示，在数据集0～9上的诊断率最低为99.32%，最高为99.58%，平均诊断率为99.53%，具有较高的故障诊断精准率。

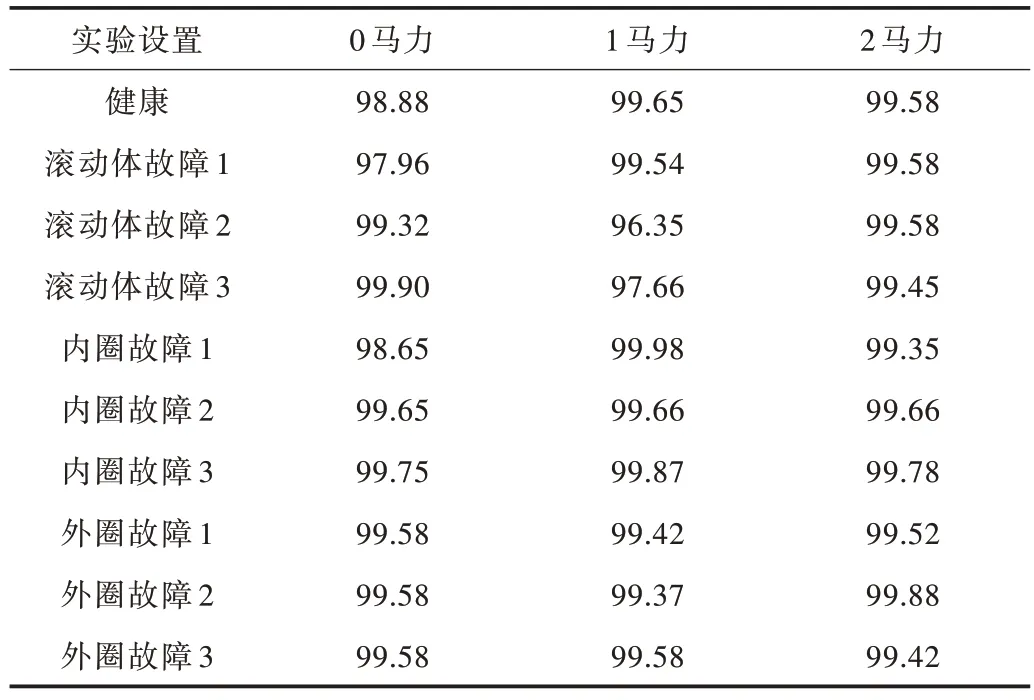
Table 4 Accuracy of fault diagnosis of different load bearings with DSGDF表4 DSGDF 模型在不同负载下的轴承故障诊断正确率 单位：%

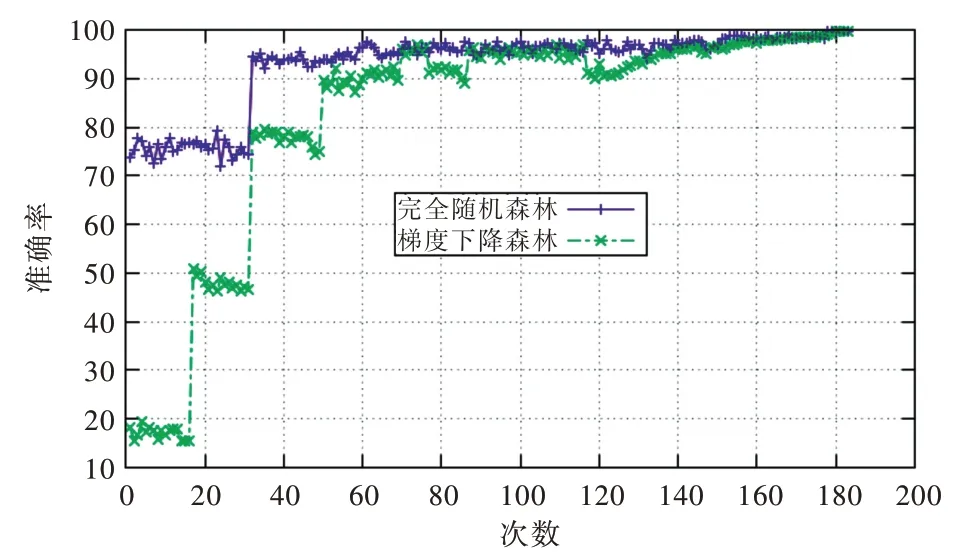
Fig.5 Learning effect of cascade structure on training set图5 级联结构在训练集上的学习效果

Fig.6 Diagnostic effect of DSGDF method on the test set图6 DSGDF 模型在测试集上的诊断效果

在诊断开销方面，为控制单一开销变量，各模型诊断效果忽略不计。图7 为各模型诊断300 万个数据点的时间开销，其中DT 的诊断时间最长，为6h，基于特征工程的方法诊断开销普遍大于基于深度学习的方法。DSGDF 模型表现出色，诊断开销最少且相较DF 模型开销降低了0.73h。

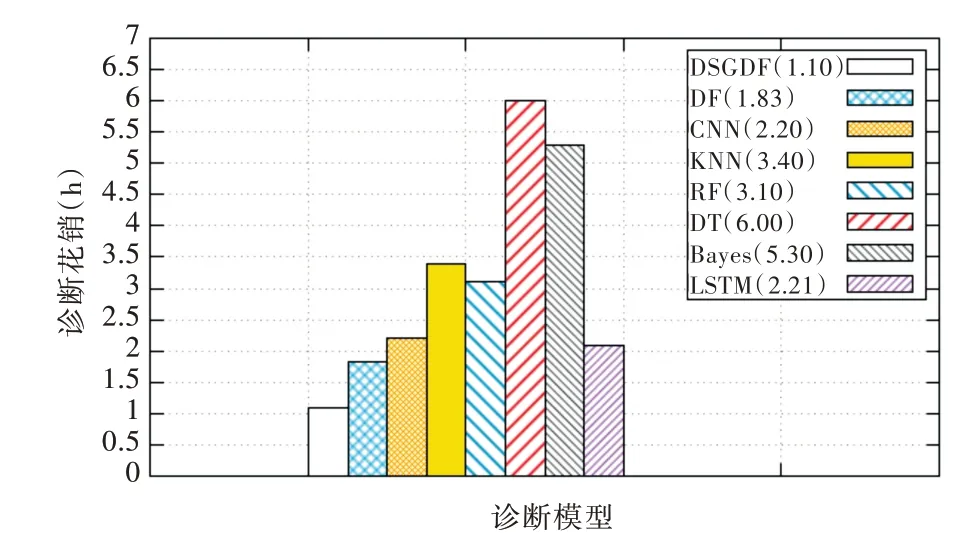
Fig.7 Cost comparison of various diagnostic methods图7 各类诊断方法开销比较

3.3.3 小样本数据故障诊断效果验证

采用4 种不同类型的小样本平均故障诊断精准率验证轴承故障诊断方法的性能，结果如表5 所示。“5 类”表示在训练模型时有1 类健康样本和4 类故障样本，且每类样本含有1 000个数据点，其余依此类推。当使用5 类样本训练模型时，KNN、DT 这类基于特征工程的方法诊断正确率最低；基于深度学习的方法，如CNN、LSTM 的诊断正确率严重受样本个数影响。使用20 类样本数据时，CNN 的诊断正确率相较使用5 类样本数据时提高了25.51%，LSTM 提高了34.00%。基于树的3 类模型RF、DF、DSGDF 受样本数据影响较小，在小样本数据为5 类时，RF 诊断正确率为83.24%，DF 诊断正确率为93.32%，DSGDF 诊断正确率为98.00%，且DSGDF 在各类小样本数据集诊断中均表现出色。

实验结果表明，训练样本数量会在一定程度上影响模型的训练效果，可能有以下两个原因：①对于大多数基于特征工程的方法来说，较少的样本数据会导致其无法多样性分割信号间隔，精准率不高；②对于大多数基于深度学习的方法来说，当样本数据较少时，超参数较多的深度学习方法会产生严重的过拟合现象。

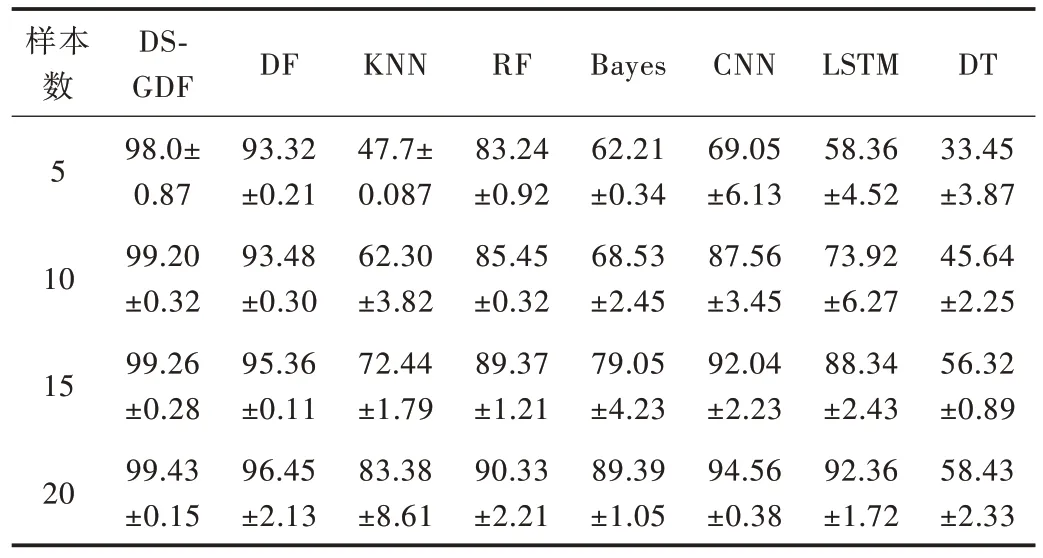
Table 5 Accuracy of fault diagnosis for small sample data of various methods表5 各类方法小样本数据故障诊断正确率 单位：%

4 结语

本文提出一种基于DSGDF 模型的轴承故障诊断方法，其通过集成深度森林模型与梯度下降算法，克服了现阶段基于深度学习模型的轴承故障诊断方法超参数多、诊断开销大、无法诊断小样本的短板，为轴承故障诊断提供了新思路。通过理论分析、实验验证得出以下结论：①DSGDF模型所需超参数较少，平均诊断F1 值在0.98 左右，证明该模型具有良好的鲁棒性与稳定性；②通过多负载变化实验以及开销验证，发现DSGDF 模型具有良好的泛化性与小开销特性；③DSGDF 模型每类诊断只含有1 000个数据点，适用于小样本故障诊断。然而，本文在实验过程中仅在CPU上对DSGDF 模型进行实验验证，未使用GPU 加速，这将是下一步研究的重点。