3台平行机上带有2个服务等级的离线负载均衡

贾珊珊，嵇雯蕙，陈智斌

（昆明理工大学 理学院，云南 昆明 650500）

0 引言

排序问题描述如下：若干个工件要在一些机器上进行加工，如何安排机器和工件使某些要求（目标函数）达到最优。一个排序问题可以用三元组

α

|

β

|

γ

来描述，其中

α

域描述机器环境，

β

域提供加工特征和约束细节，

γ

域描述最小化或最大化的目标函数。对于平行机排序问题，

α

域用

P

表示，

β

域可能包括多项，如提交日期、机器适用约束等；

γ

域一般采用最大完工时间

C

等作为目标函数。经典的平行机排序问题（Multiprocessor Scheduling，MS）问题可表示为

P||C

。根据实际情况研究人员相继提出了带惩罚费用的排序问题

P|rej|C

和带等级约束的排序问题

P|GoS|C

，本文研究的是带等级约束的平行机排序问题。在日常服务业中，通常把客户归类为白金、黄金、白银和正式成员，等级越高客户享受越好的服务，提供区分服务的一个方法是给服务者（如：机器）和客户（如：工件）贴上带有服务等级的标签，并且服务者只为等级不低于自己的客户提供服务，并希望在最短的时间内为所有客户完成服务。对于此类有等级限制的问题，经典的平行机排序已经不适用，需要考虑的是等级约束下的负载均衡问题（

P|GoS|C

）。当所有任务的服务等级都相同，并且任务的服务等级都大于等于机器的服务等级时，本文讨论的问题就变成了经典的平行机排序问题

P||C

，所以本文讨论的问题仍然是强NP-难的问题。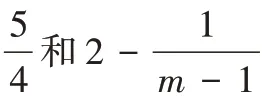

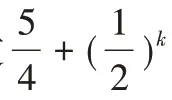
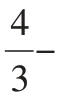
1 符号说明及问题描述

1.1 符号说明

部分符号说明如下：

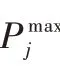
T

：所有工件的加工时间总和

S

、

S

：等级为1、等级为2 的工件集合

n

、

n

：等级为1、等级为2 的工件个数

D

：多出部分的工件集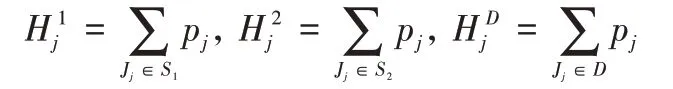

1.2 带服务等级的负载均衡问题（P|GoS|Cmax）

本文考虑服务等级负载均衡问题的一种特殊情况，3台机器两个等级约束的负载均衡问题（

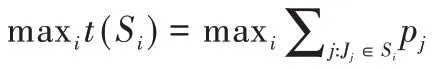
P

|GoS

|C

）。显然，该问题可分为以下4 种情况进行讨论：情况（1）：当

g

(

M

)=

g

(

M

)=

g

(

M

)=1，

g

(

J

)=1或2时，所有工件都可放在这3台机器上加工，等同于经典平行机排序问题。情况（2）：当

g

(

M

)=

g

(

M

)=

g

(

M

)=2，

g

(

J

)=1或2时，只考虑

g

(

J

)=2 的工件，等同于经典平行机排序问题。情况（3）：当

g

(

M

)=1，

g

(

M

)=

g

(

M

)=2 且

g

(

J

)=1或2 时，记该问题为

P

|GoS

(

M

)

|C

。情况（4）：当

g

(

M

)=

g

(

M

)=1，

g

(

M

)=2 且

g

(

J

)=1或2 时，记该问题为

P

|GoS

(

M

)

|C

。

2 算法说明

为了更好地说明算法，首先介绍LPT算法。

算法1

最小时间跨度排序

将工件按照加工时间从大到小进行排序

按照这个次序在机器上对工件排序，将工件放在当前负载最小的机器上

下面围绕情况（3）和情况（4）展开，并针对这两种情况设计近似算法。

2.1 P3|GoS(Mi)1,2,2|Cmax

2.2 P3|GoS(Mi)1,1,2|Cmax

算法3

问题

P

|GoS

(

M

)

|C

的一个2-近似算法

3 算法近似比证明

3.1 等级约束为1、2、2 的3台平行机

工件

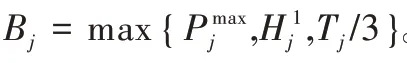
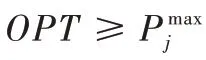
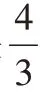
J′

刚好出现在

M

上的情况，如图1 所示。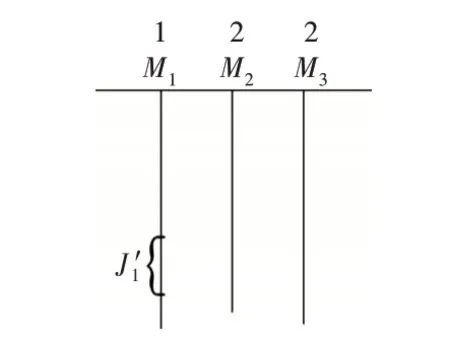

Fig.1 Workpiece J′1 on machine M1图1 工件J′1 在机器M1 上

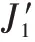
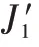
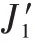
Fig.2 Workpiece on machine M2图2 工件在机器M2 上

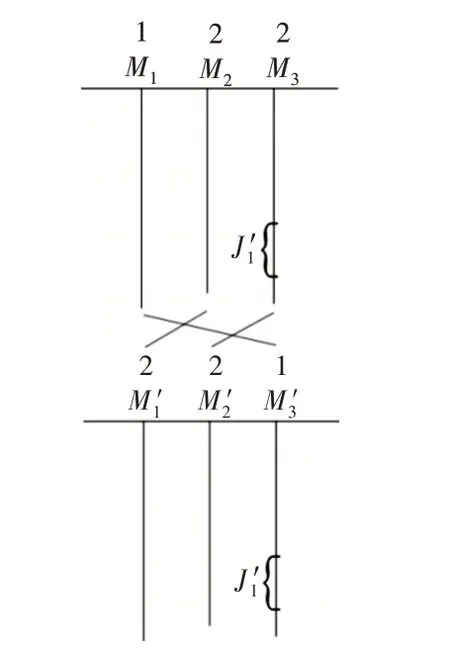
Fig.3 Workpiece on machine M3图3 工件 在机器M3 上

3.2 等级约束为1、1、2 的3台平行机

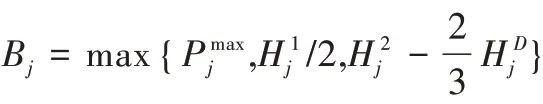
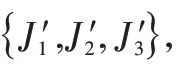
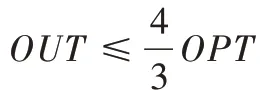
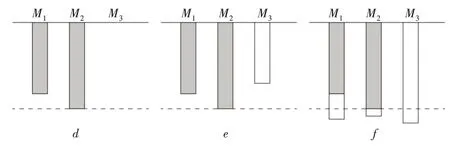
Fig.4 General cases with level constraints of 1，1 and 2图4 等级约束为1、1、2 的一般情况

4 结语

本文研究了具有等级约束的离线平行机排序问题，目标为最小化机器的最大完工时间。通过对LPT算法的深入研究，在该算法基础上设计出新的算法，解决了3台平行机上带有2个服务等级的离线负载均衡问题，并证明了近似比。但是本文只研究了3台机器的情况，后续可以进一步推广到

m

台机器。