基于改进的A*算法机器人导航路径研究

胡广雪 郑亚清 韩洋祺

摘要：针对移动机器人在不同的工作场景不确定性，设计了将相邻节点优先级分组与Floyd-Warshall算法相结合路径规划研究方法。首先，对全局规划A* 算法相邻节点优先级分组。其次，综合环境和路径的情况以全局路径的拐点为局部目标点，采用改进的Floyd-Warshall算法进行局部路径规划，从而使规划路径寻路时间及转折点次数优于A*算法。最后进行仿真验证，仿真结果表明：该算法有效解决复杂移动环境的路径规划的问题，提高了机器人导航路径规划的准确性和鲁棒性。

关键词：移动机器人;改进的A*算法;路径规划

1.引言

随着智能制造技术的不断发展，机器人在在野外探测、工业流水线制造、物流输送等多个领域广泛应用。其中，定位和导航系统是研究机器人的核心问题。智能移动机器人系统主要由环境感知、环境逻辑决策及辅助路径规划系统组成，且导航路径规划是移动机器人性能衡量的重要指标。目前也有一些其他导航定位方法，一些学者采用人工路标定位，但此类定位方法需要提前布置导航的室内场景[1]。[2]通过改进A* 算法的关键节点实现了静态移动环境下的路径规划。[3-6]根据已知和未知环境信息进行局部和全局路径的规划。[7]提出了基于二次规划改进的A*算法，但并未考虑移动机器人的体积和偏转角，实际应用不强。[8]提出跳过节点搜索策略，减少了计算过程中访问节点数，加快程序的运行速度，但路径中转折点仍比较多。采用改进蚁群算法搜索全局路径点，但搜索节点数据量太大。提高控制程序运算速度，但对行驶路径的弯曲程度没有考虑。

针对传统算法计算量大，由于地下车库和不同工作厂房复杂不确定性，为了提高智能移动机器人在位置环境中精确性，本文采用改进的A*算法进行智能移动机器人导航路径规划，为实现高效率的工作提供实现基础。

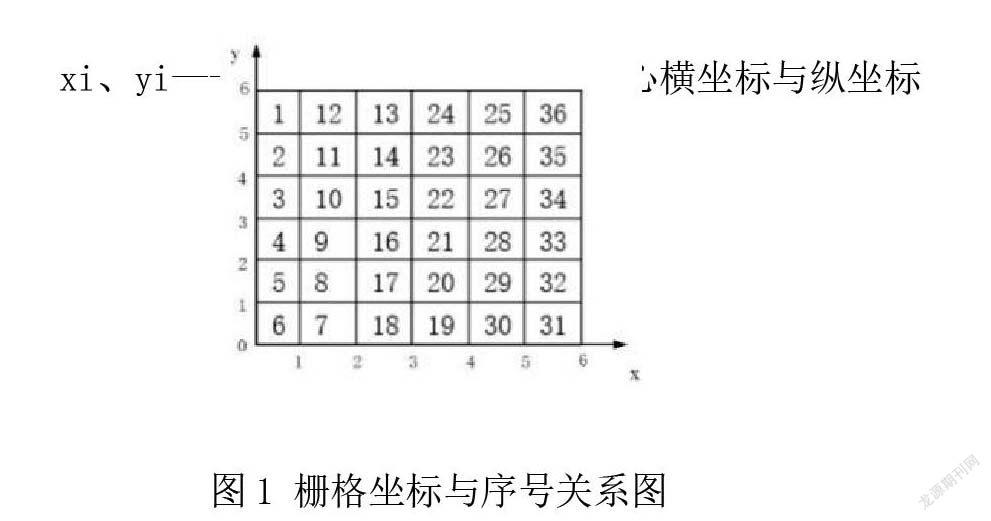
假设智能移动机器人M在有限个障碍物的二维栅格平面区域Y内移动，以Y的左下角为坐标原点，以水平方向为横坐标x轴，垂直方向为纵坐标y轴，建立如图1直角坐标系xOy。其中，xmax、ymax分别为横纵坐标轴方向上的最大值。以移动机器人的步长s对坐标区域进行划分行和列的栅格数。

每个栅格有相应的坐标值与其一一对应，将其序号集定义为，以坐标区域的左上角为原点，由左向右、自上至下，对二维平面区域Y进行编号，坐标与序号之间的关系为

2.改进的A*算法

由于传统的A* 算法存在运行求解速度较慢，当移动机器人从栅格A移动到栅格B时，考虑到移动机器人有一定的轮廓体积，因此，在红点处可能会发生碰撞，从而造成移动机器人损坏。对此，本文通过对传统的A*算法节点的扩展顺序进行改进，如图2所示。设移动机器人当前运动环境节点为O，周围相邻节点分别为 A、B、C、D、E、S、W、N。以便降低在实际移动过程中与障碍物发生碰撞的概率，相邻两个节点优先分组。

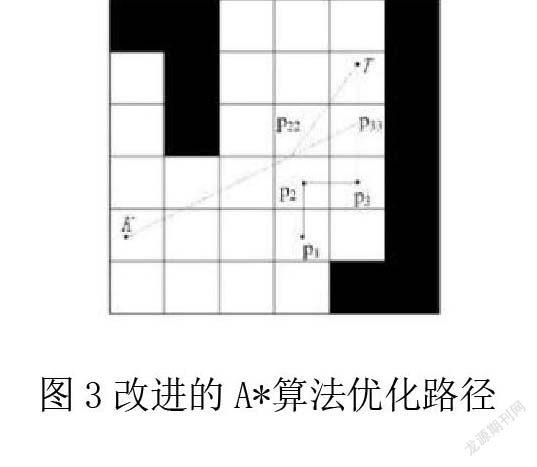
上述方法对A*算法子节点的选择优化，可以提高移动机器人规划路径的安全性，但路径规划过程中转折次数较多，行驶路线的不平滑难度增加很多。针对上述问题问题，在优化选择子节点的基础上，将双向平滑理念引入到Floyd-Warshall 算法中对 A* 算法进行改进，通过建立两点之间路径长度的二维数组来计算最短路径。将双向平滑理念引入到 Floyd-Warshall 算法中，即在优化正向路径的基础上，加入目标点 T 到起始点 K 的反向优化。具体改进步骤如图3 所示。

针对改进的A*算法优化路径算法，主要从以下步骤进行仿真验证：对路径中同一直线上的中间冗余节点进行删除，仅保留起始点K、拐点和目标点T。删除冗余节点后的移动路径为 K→p1→p2→p3→T。从起点K开始，在保留节点pi、pj之间每q步取一节点，判断取的节点与上一路径节点之间是否存在障碍物。若有障碍物，则当前路径节点不变;若无障碍物，则由程序计算障碍物与节点pi、pj连线的距离。

根据栅格的大小将规划的路径安全距离定义为d，当d>dOB时，该路径可以进行选择，否则该路径不可选，加入安全距离后的路径为K→p33→T。

3.仿真结果验证

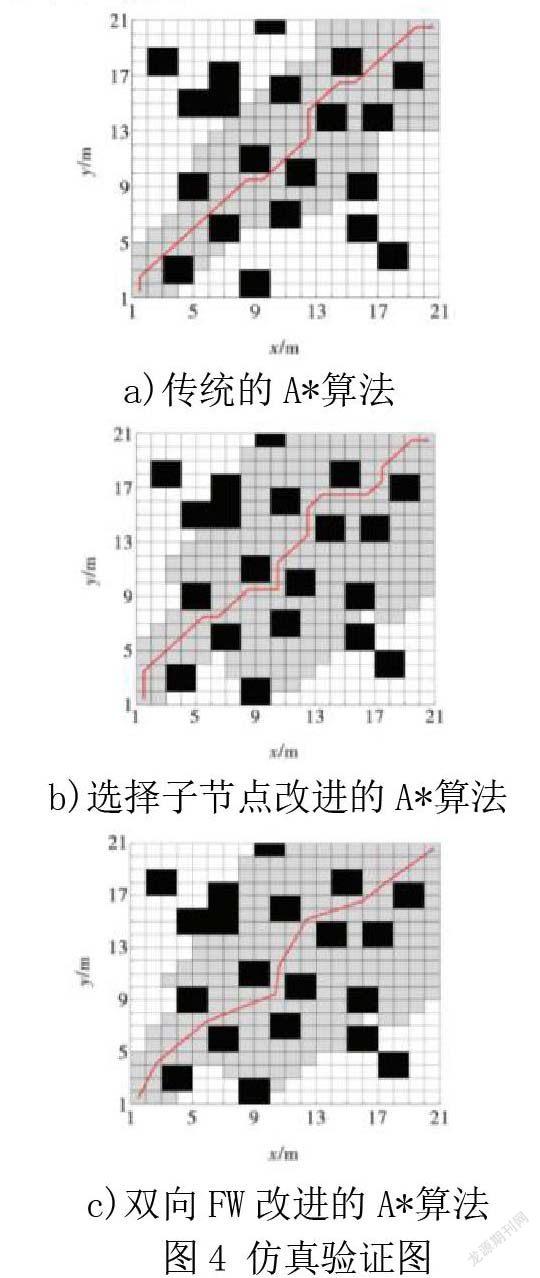
为验证上述理论分析及改进 A* 算法规划路径的有效性，在 Matlab 2010a实验平台下分别对传统的 A*算法。其中 d = 0.8 m，q = 0.1 m，栅格大小为1 m。黑色栅格为障碍物区域，占地图总面积为19.5%，灰色栅格为遍历的节点区域，两组栅格地图路徑规划结果如图4所示。

由仿真的路径曲线可得，传统A*算法所规划的移动路径存在斜穿障碍物顶点的不足，适应性较差。改进后的A*算法在设定机器人行驶的安全距离后，规划路径与障碍物的距离始终大于d，从而避免了移动机器人距障碍物较近而发生碰撞的情况，提高了移动机器人路径行驶的安全性。基于双向FloydWarshall改进的A*算法折点的数量较传统A*算法有所减少，其规划的移动路径曲线更加平滑，在实际应用中，有利于减少移动机器人运动过程中的航向角，有效提高移动机器人运动的平稳性和工作效率，具有一定的实用价值。

4.结论

（1）为提高A*算法的运行效率及移动机器人规划路径的安全性，提出对子节点的扩展的顺序进行优化选择，将8个领域节点划分为高级组和一般组，缩短寻优路径的时间，避免规划路径存在斜穿障碍物顶点问题。

（2）针对传统的A*算法搜索路径转折点个数多、路径曲线不平滑等不足，采用 Floyd-Warshall算法对路径曲线进行双向平滑处理，从而减少航向角的次数，改善行驶路径的质量。

（3）采用Floyd-Warshall算法改进后的的A*算法，符合移动机器人的运动控制，具有实际的使用价值。

参考文献：

[1]黄露.基于人工路标的室内机器人导航方法研究与实现[D].中国科学技术大学，2017.

[2]王帅军，胡立坤，王一飞.基于改进D*算法的室内移动机器人路径规划[J]. 计算机工程与设计，2020，41（4）：7.

[3]Baoye， Song， Zidong， et al. On Global Smooth Path Planning for Mobile Robots using a Novel Multimodal Delayed PSO Algorithm[J]. Cognitive Computation， 2017， 9（1）：5–17.

[4]Chen H ，Fei J . UAV Path Planning Based on Particle Swarm Optimization with Global Best Path Competition[J]. International Journal of Pattern Recognition and Artificial Intelligence， 2017， 32（1）.

[5]Golda A F ，Aridha S ， Elakkiya D . Algorithmic agent for effective mobile robot navigation in an unknown environment[C]// Intelligent Agent & Multi-Agent Systems， 2009. IAMA 2009. International Conference on. IEEE， 2009.

[6]Mohtasham S K ， Abbas S . Adaptive Path Planning for Navigation and Sensing of Micro Aerial Vehicles.  2016.

[7]楊璐， 汪博涵， 张雪洁. 基于A*算法的AGV路径规划研究[J]. 公路与汽运， 2014.

[8]Pal A ， Tiwari R ， Shukla A . Modified A* Algorithm for Mobile Robot Path Planning[M]. Springer Berlin Heidelberg， 2012.