四面体的界心
曾建国
(赣南师范大学数学与计算机科学学院 341000)
文[1]中,笔者把三角形的奈格尔(Nagel)点[2]概念及性质引申推广至有棱切球的特殊四面体中.本文拟将奈格尔点概念进一步引申推广至一般四面体中.
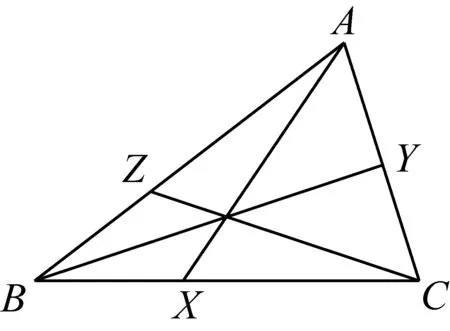
图1
三角形的奈格尔(Nagel)点被国内作者称为三角形的“界心”[3~10]——这是由三角形的三条“周界中线”交于一点而得名(同一个三角形的界心与奈格尔点是同一点,以下统称为三角形的界心).即有(如图1)
定理0[3]过△ABC的顶点A、B、C与对边上一点X、Y、Z作线段,使之平分△ABC的周长,则(周界中线)AX、BY、CZ交于一点.
对上述性质进行类比,我们可以将三角形界心的概念及性质引申推广至任意四面体中,即有
定理1过四面体A1A2A3A4的棱AiAj和它的对棱上一点作截面πij(1≤i 定理1的证明需要下面的: 引理(空间塞瓦逆定理)[11~12]在四面体A1A2A3A4的棱AiAj上取一点Bij(1≤i 成立,则六个平面A1A2B34、A1A3B24、A1A4B23、A2A3B14、A2A4B13、A3A4B12交于一点N. 定理1的证明如图2,设所作四面体A1A2A3A4的各周界中面与棱AiAj交于点Bij(1≤i 图2 由题设,截面A1A4B23平分四面体A1A2A3A4的表面积,则 同理可得 则 同理可证 根据引理可知,六个周界中面πij(1≤i 由于本文得到的“任一四面体六个周界中面交于一点”这一结论很好地类比了三角形界心的概念及性质,因此,我们有理由将本文定理1中的任一四面体六个周界中面的交点N称为四面体的界心. 细心的读者也许注意到,文[1]将三角形的奈格尔(Nagel)点概念及性质引申推广至有棱切球的特殊四面体中,得到了“三组对棱之和相等”的四面体的奈格尔点概念;文[13]则用向量法定义了一般四面体的奈格尔点概念,这些四面体的奈格尔点与本文所得到的一般四面体的界心是否为同一点?这是值得进一步研究的问题.

